Wave equation is NOT an electromagnetic wave equation

Wave equation is NOT an electromagnetic wave equation

Annotation

It is shown that the wave equation only in the first approximation can be considered the equation of an electromagnetic wave, and therefore it is offered a new equation is proposed for electromagnetic wave, which also follows from the system of Maxwell's equations. This equation demonstrates the strict observance of the law of conservation of energy, the phase shift between electric and magnetic intensities, the conversion of energy from magnetic to electric and vice versa, the twist of an electromagnetic wave.

First of all, we note that the Maxwell system of equations (MSE) is a system of differential equations and therefore can have many correct mathematical solutions. Among them there may be those that correspond to experiments and physical laws, and those that contradict experiments and physical laws. The wave equation is one of the latter.

The MSE solution for vacuum should

• 1.    not contradict the law of conservation of energy at every moment of time , i.e. establish the constancy of the flux density of electromagnetic energy in time,

• 2.    demonstrate a phase shift between electric and magnetic intensities,

• 3.    demonstrate the conversion of energy from magnetic to electrical and vice versa,

• 4.    explain the twist light , i.e. the appearance of an orbital angular momentum, at which the energy flow does not just fly forward, but rotates around the axis of motion.

However, the solution in the form of the wave equation

• •    contradicts the law of conservation of energy, because in it, the energy flux changes in time and retains its value only on average , which, in principle, cannot be considered compliance with the conservation law - see Fig. 1;

• •    demonstrates the inphase of electrical and magnetic intensities -see Fig. 1;

• •    does not explain the twist light.

In [1], a solution of the Maxwell equations for vacuum in the cylindrical coordinate system (г, ф, z} was found, which has the following form:

Hr.= hT(r) co ,                                    (1) Н ф .= h ф (r)si ,                                    (2) H z .= h z (r)si ,                                             (3) E r .= e r( r)si ,                                        (4) Е ф .= 6 ф (г)со ,                                    (5) E z . = 6 z (r)co ,                                               (6)

where

co = cos( аф + yz + tot) ,                     (7) si = sin( аф + yz + tot) ,                       (8) y = toV^c ,                             (9) 6 z (r) = 0 ,                                           (10) /l z (r) = 0 ,                                             (11) er(r) = сф(г) = 0. 5Ar(a-1), A - const ,         (12) к ф (r) = J | e r (r) ,                                 (13) h r(r) = - J | e r (r) ,                              (14) A, a, to - const .

The same system of equations in the Cartesian coordinate system ⁽ x, y, z ^} has the form

Ex = exsin((a + 1)ф + yz + tot),(15)

Ey = eycos((a - 1)ф + yz + tot),(16)

Hx = h xcos((a + 1)ф + yz + tot),(17)

Hy = hysin((a - 1)ф + yz + tot),(18)

where

ex(r) = ey(r) = 0.5Ar(a 1) ,	(19)
h x ( r) = h y ( r) = -J | e x ( rX	(20)
r = ^x2 + y2 ,	(21)

Ф = arctg^y/x)).                             (22)

In these decisions

• •    the energy flux density along the z coordinate at each radius Г retains its value at each moment of time - the energy conservation law is observed,

• •    there is a continuous process of converting energy from magnetic to electrical and vice versa,

• •    the locus of points of equal intensity (magnetic or electrical) at each radius is a spiral - see Fig. 2

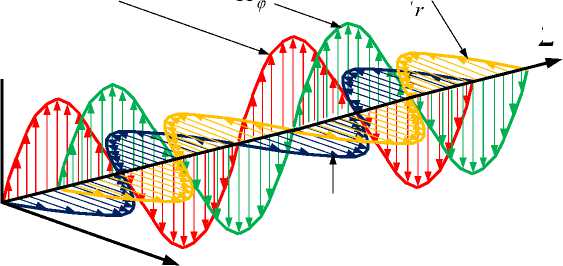
• •    there is a phase shift between the electric and magnetic intensities - see Fig. 3,

• •    the twist of the electromagnetic wave is observed - see Fig. 4.

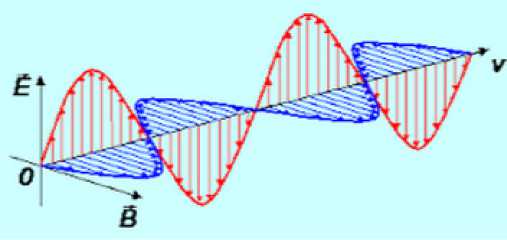
Fig. 1.

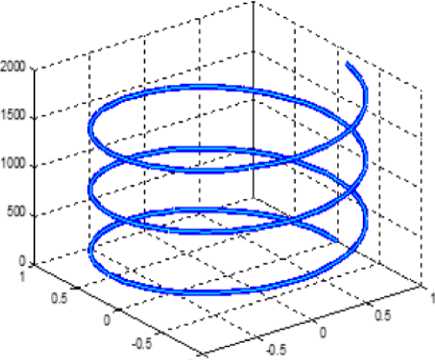
Fig. 2.

ϕ

H

E

E ϕ

z

H r

Fig. 3.

r

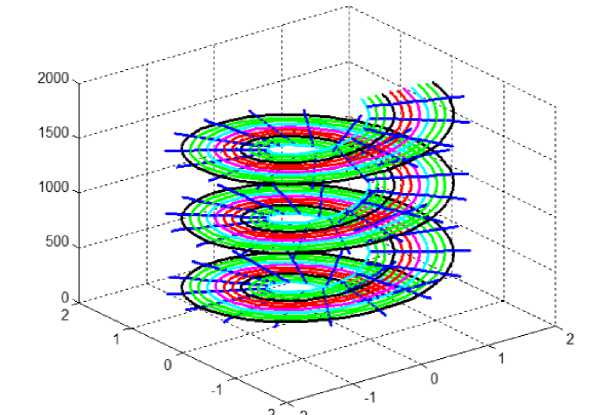
Fig. 4.

Consider also the spherical coordinate system {p, 0, ф) . In this case, the solution of Maxwell's equations for vacuum has the following form:

E, = еф Kh(p, 9) sln(x p + xp + cot),(23)

E, = 69Kh(p, 9) cos(x p + xp + cot),(24)

Ep = 0,

H, = h,Kh(p, 9) cos( x p + xp + cot),(26)

H = h,Kh(p, 9) sin( x p + xp + cot),(27)

Hp = 0, where Kh(p, 9) is a definite function, e,, 6,, h,, h6 are constants, and h„ - J"6», h« - J)r., to ,— / - -Veil.

The function Khm(0, к) is defined by an equation of the form (cos(0)±K)Khm(0, к) + sin(0)  Khm(0, к) — 0,

In the general case, this differential equation has no analytical solution. In fig. 5 shows the functions Khm(0, к ) for different values of K. For comparison, the sin(0) function is shown as dots.

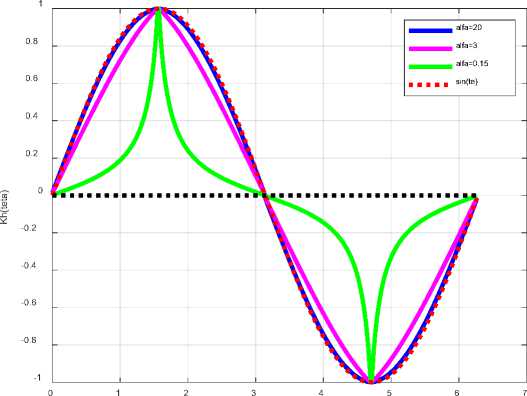
Fig. 2. teta (KhTest.m)

Fig. 5.

In this decision

• •    the density of the energy flux passing through the sphere does not depend on the radius and does not depend on time; this flux has the same magnitude on a spherical surface of any radius at any time; in other words, the energy flux directed along the radius retains its value with increasing radius and does not depend on time, which corresponds to the energy conservation law;

• •    there is a phase shift between electric and magnetic intensities;

• •    the twist of the electromagnetic wave is observed.

A huge number of theoretical conclusions in electrodynamics are made based on the use of the wave equation. These conclusions were obtained in violation of the law of conservation of energy and had to put up with it. Now that the exact solution to Maxwell's equations has been found, it is necessary to revise and refine the previously obtained results. This is necessary because some of the results may turn out to be fundamentally incorrect (and not just erroneous with some error).