Wavelet Adaptive Reduced Order Observer Based Tracking Control for a Class of Uncertain Time Delay Nonlinear Systems Subjected to Actuator Saturation
Автор: Manish Sharma, Ajay Verma
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 12 vol.4, 2012 года.
Бесплатный доступ
This Paper investigates the mean to design the reduced order observer and observer based controllers for a class of delayed uncertain nonlinear system subjected to actuator saturation. A new design approach of wavelet based adaptive reduced order observer is proposed. The proposed wavelet adaptive reduced order observer performs the task of identification of unknown system dynamics in addition to the reconstruction of states of the system. Wavelet neural network (WNN) is used to approximate the uncertainties present in the system as well as to identify and compensate the nonlinearities introduced in the system due to actuator saturation. Using the feedback control, based on reconstructed states, the behavior of closed loop system is investigated. In addition robust control terms are also designed to attenuate the approximation error due to WNN. Adaptation laws are developed for the online tuning of the wavelet parameters and the stability of the overall systems is assured by using the Lyapunov- Krasovskii functional. A numerical example is provided to verify the effectiveness of theoretical development.
Wavelet neural networks, reduced order observer, adaptive control, delayed systems, actuator saturation, Lyapunov- Krasovskii functional
Короткий адрес: https://sciup.org/15010341
IDR: 15010341
Текст научной статьи Wavelet Adaptive Reduced Order Observer Based Tracking Control for a Class of Uncertain Time Delay Nonlinear Systems Subjected to Actuator Saturation
Published Online November 2012 in MECS
In many practical systems, the system model always contains some uncertain elements; these uncertainties may be due to additive unknown internal or external noise, environmental influence, nonlinearities such as hysteresis or friction, poor plant knowledge, reduced-order models, and uncertain or slowly varying parameters. Hence, the state observer for the uncertain system will be useful and apply to reconstruct the states of a dynamic system. The means to design adaptive observers through estimation of states and parameters in linear and nonlinear systems has been actively studied in recent years [1-3].Adaptive observers of nonlinear systems have attracted much attention due to their wide uses in theory and practice.
Observers may broadly be classified in two categories. The first class is so-called full order observer which estimates all states of the system, including the measurable states which are the outputs. Obviously this redundant estimation of measurable states is not necessary, and conversely it might increase the complexity of the observer design and practical realization. That is the reason why the second class of observers was introduced, named as reduced order observer, which, different from full order observers, needs to estimate only unmeasurable states of the studied system [4-7].
Some complex behaviors like limit cycles, chaotic behavior and even instability are induced due to presence of the time delay in the system [8-10]. The presence of delay effect complicates the analysis and design of control systems. Moreover, time-delay effects in the state vector, especially in the control input degrade the control performances and make the closed– loop stabilization problem challenging.
Characteristics of practical actuators are in general nonlinear, usually described by the nonlinearities like saturation, hysteresis backlash etc. Nonlinear behavior of the actuator causes the detuning of plant as well as controller parameters which may lead to the poor performance or even may cause the destabilization of the system. Out of these nonlinearities saturation is the frequently encountered nonlinearity and is addressed by several researchers Most of the research in this topic is based on augmentation of baseline controller with additional saturation compensation dynamics [11-13].
System identification plays a critical role in the designing of controllers for uncertain nonlinear systems. Controller is expected to provide efficient, safe and desired performance. To design such a controller a highly accurate model of the system is required which is quite difficult due to modeling inaccuracies. In such cases intelligent control tools are integrated with the control strategies to obtain reliable and accurate control performance. Since last decade wavelet networks have attracted much attention of researchers. A wavelet network is constructed as an alternative to neural networks as a system identification tool. Wavelet network integrate the space frequency localization property of wavelets with learning capabilities of neural networks to improve the function approximation ability. Wavelet networks finds application in multi-scale analysis and synthesis, time frequency signal analysis in signal processing, identification of nonstationary signals [14-15]. Due to its property of multi resolution analysis and suitability for the development of online tunable control laws, an adaptive wavelet based control strategies are cited in the literature [15,16].
This paper deals with the designing of wavelet reduced order adaptive observer and an observer based controller for a class of uncertain time delay nonlinear systems subjected to actuator saturation. WNN is used for approximating the system uncertainty as well as to identify and compensate the saturation dynamics.
The paper is organized as follows: section II deals with the system preliminaries, system description is given in section III. Reduced order observer and controller designing are discussed in section IV and V respectively. Stability aspects are analyzed in section VI. Effectiveness of the proposed strategy is illustrated through an example in section VII while section VIII concludes the paper.
-
II. System Preliminaries
2.1 Actuator Saturation
The output of an actuator u ( t ) with input v ( t ) subjected to the condition of saturation is defined as
V > u
max
u = t V
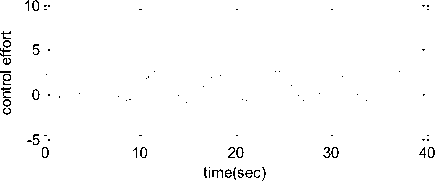
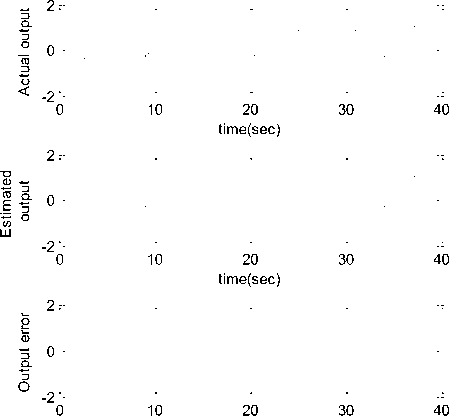
U min V< u min where u and u are upper and lower saturation max min limits as shown in the fig1. For symmetric actuator saturation u^n = -umm .Part of the control effort which can not be implemented under this condition is defined as umax-v V > u max Au = - u - umin-v V < u min where Au describes the effect of actuator saturation and can be effectively approximated by using a self recurrent wavelet neural network. Wavelet network is a type of building block for function approximation. The building block is obtained by translating and dilating the mother wavelet function. In contrast to conventional wavelets, a biased wavelet has a nonzero mean and can better reproduce signal components that are in the low-frequency region on the time-frequency plane since the nonzero mean enlarges low-frequency gain. Output of a biased n dimensional wavelet network with m nodes is f = a T ф( x, w, c ) + P T ф( x, w, c) (3) where x = [xt,x2,...,xn]T eRn is the input vector, ф = [ф1, ф,,..., ф m ] T e^ m and ф = [ф, ф,,..., Фт ] T e^ m e wavelet and bias functions respectively; w = [w1, w2,..., wm]T e Rm” and c = [c.,c2,...,cm ]T e Rm" are dilation and translation parameters respectively ; a = [a.,.., am ]T e Rm and в = [pj,..,вm ]T e Rm are weights of wavelet and bias function respectively. Let f*be the optimal function approximation using an ideal wavelet approximator then f = f * +A = a*T ф* +p*T ф’+А (4) wher ф* =ф( x, w *, c *) and ф* =ф( x, w‘, c *) , a’,в’, w*, c*are the optimal parameter vectors of a,p, w, c respectively and A denotes the approximation error and is assumed to be bounded by |A| < A’ ,in which A’ is a positive constant. Optimal parameter vectors needed for best approximation of the function are difficult to determine so defining an estimate function as , ф = ф(х,№,с),ф = ф(х,н>,с) , 6iAw,c where and are the estimates of a*, P*, w\ c* respectively. Defining the estimation error as where . By properly selecting the number of nodes, the estimation error f can be made arbitrarily small on the compact set so that the bound f < fm holds for all x e ^ . Using Taylor expansion linearization technique to transform the nonlinear function into a partially linear form as a step towards the derivation of online tuning laws for the wavelet parameters to achieve the favorable estimation of system dynamics [9] 6 = ATw + BTc + h 1 1 1 (7) ф = A^w+B^c + h Where and h, h are the vectors of higher order terms and ^Ф, dw ^Ф, de d^. d^.d^ 0.. .0 —, 0.. .0 ^1, ^2.^ ' А АА _ dto, d^d(Dj 0...0—,——,....——,o...o . dcu dc2i dcni _ ^4= o о ^^ ^ dw dwu ’ dw2i Ao...o ^ Substituting (7) into (6) where the uncertain term is given by following expression ah + a TATw* + a T BT c * +^ vP*Th2 + PT ATw + PTBTc * v Consider a nonlinear system of the form x = x2 x 2 = x3 Xn = f (x (t), x (t - r)) + u y = Cx where are state variable, control input and output respectively. f (x) : ^n ^ ^ is a smooth unknown nonlinear function. r is the known time delay. Rewriting the system (9) as x = Ax + B(f(x(t), x (t- r)) + u ) У = Cx where "0 1 0 • 0" "0" 0 0 1 0 0 A= 0 0 0 1 , B= 0 , c = [1 00 _0 0 0 .. 0 _ .1 _ Also x g^n and y g ^p . For all real time systems, p < n . Using the actuator saturation defined in section II system (10) can be transformed to A12 A22 J _ y = [ C11 C12 ] m + B11 B 21 _ W x, yd) + V) = У1 +У 2 x = Ax + B (5( x, yd ) + v) y = Cx u where ^(x, yd ) = f (x(t), x(t -t)) + Au . Suppose that C has full rank, it is possible to make a linear change of coordinates = Ax = x where xmg ^p is the measured state, xug ^n p is the unmeasured state and y g ^p is the output of the system (11) which depends upon measurable states as well as unmeasurable states and it is assumed that both the parts of the output, y and y are explicitly available for measurement. Wavelet based reduced order observer that estimates the states of the system (11) is given by where Q is chosen so that Л is an invertible matrix. Also ^ g^p and £ g^n-p . Applying the coordinate transformation (12), the plant (11) takes the form ^m J F^m , ^u ) F2(^m Л ) У = ^(^m Л ) where F (£) = f (Л-1^). The motivation for the reduced order observer stems from the fact that in the plant model (11), the state ^ is directly available for measurement and hence it suffices to build an observer that estimates only the unmeasured state ^ . The order of such an observer will correspond to the dimension of the unmeasured state, namely n - p< n . This type of observer is called a reduced order observer [18] and it has many important applications in design problems. The objective is to formulate a state feedback control law to achieve the desired tracking performance. The control law is formulated using the transformed system ni т (11) . Let be the vector of desired tracking trajectory. Following assumptions are taken for the systems under consideration. Assumption A1 Desired trajectory y(t) is assumed to be smooth, continuous Cn and available for measurement. Applying the linear transformation (12), the system (11) takes the form = Л^.^ + мЦ2 (x„ - x„) + S21H + 5215 where xˆ is the estimation of state vector xu,m = _mx,m2,...,mn_^J is the observer gain matrix, selected such that the matrix A2 - mA2is stable. In this work WNN is used for system identification. Rewriting (15) as ^„ +rn(xm ~^xm-^1(/’(x)+u)-^)+^1M+^1S Or equivalently Note that the above equation contains xˆ for the design of observer which is not available for the design. So the given transformation has to be applied to generate an intermediate state. xU = ^xu - mxm Applying the above transformation, the observer takes the form Assumption A2 a) H( x(t)) - 5( xx(t X)! < Y11 |xu 11 + /4 b) For a symmetric positive definite matrix Q there exist a symmetric positive definite matrix P such that (A2 - mA2) TP + P (A2 - mA 2) = - Q and (PB2,)T = C where xu = xu - 5cu is the unmeasurable state variable estimation error while y is a positive constant. Now defining the error system as xu = (A22- mA12)xu + B(8(x) - 8(x)) y = C12 xu = y 2 With the help of the proposed tuning laws presented in the next part of this subsection, the error term 8(x(t), x(t - тУ) is reduced to a small arbitrary value which is further attenuated by robust control term v . Tuning laws are given as: (i) Adaptation laws for the wavelet network used to approximate 8(x) will be: 1T 12 1 T 1 T 1 T V = - x.Px + - r + - П1а5а5 + - П2 c5c5 + - Пз ws ws t (23) + j w(a)da t-т Differentiating it along the trajectories of the system к = -^x^Qxu + xT„PB^S(x)-5(x^ + +r(Kmem + Kueu + К(5(x) + и(0 + т<уг - Cx„) - j,) +'7i as = -a5 = A >2 (% -ftk - ft5) ^=ft = ftft ^S — ^5 — P^ 4^1?8 where в, в, в are the learning rates with positive constants. The robust control term is defined as v = У 2( P2 + 1) r 2P2 where p is the prescribed attenuation. Substituting control lawu in the above equation = " <2™ Н || + £РВп № - 5(х) + 5(х) - vr) + r(y, - к,г) +r)1aI5a6 + Пгстбс5 + Пз^'б + '*<л„ (0) - «’(х. (/ - г)) 5 "^™ НЦ + Ч ||х„|Г +М, ||.YU||2+Mj ||х„||||х„(/-т)|| +PuPB1^S(x)-vr)+M4+K-krr') + niaI5«5+n/scs +'7з3Ч1^ + 1'<хи (0) - и<хт(t - г)) M1 =||PB21| |/з, M 2 = PmaxYl, M3 = Pmax/2, M 4 = max ^г| + /4 and/1,/2,Y3,Y4 ^ 0 V. Basic Controller Design using Filtered Tracking Error Defining the state tracking error vector eˆ(t) as e(0 = x(0 - i; (0 = em (/) + eu (0 The filtered tracking error is defined as ’ Kmem+KA where Km = [k1, k2,__ kn- - p-1 ] and Ku = [ ki, k 2,-k-1 ] are the appropriately chosen coefficient vectors such that e ft 0 exponentially as ^ > 0. Applying the feedback linearization method the control law is defined as where Kr =[0, kx, k2,..., kn_ J. Stability of the system (9) with the proposed observer and controller strategy will be analyzed in the next section. Consider a Lyapunov-Krasovskii functional of the form Substituting the adaptation law and robust control term in above equation, ^ -12m,n I xu2 11 +M1 IIxu 112 +M 2 IIxu 112 +M 3 IIxm || llxm(t- T )|| + P" ^ — yi+ M 4— k^r2+ w (x™ (t)) — w(X™ (t — т)) Applying Young’s inequality in the fourth term of the above equation, Mз|Ixmllllxm(t- T)ll ^ M3^11 |x.l I1 + MT II x.< t - T)l 2P Selecting w(xm (t)) = M3^ ||x„ 112results in 2^ S -1 e_ 1 |x;| + (M, + M 2)1 Ixu Г+ (Mx^- + —2 )l lx. I’ 2 22 +p2 ^2 - y2+m4 - krr2 2 8 2 The system is stable as long as krr"2 + yi + 1 Qmin Ixu2 I - (M1 + M2 ) Ixu 112 M3 p M2 +ft- + ft Ixmll + ^£S + M4 2 2 Lv^ VII. Simulation Results Simulation is performed to verify the effectiveness of proposed WNN reduced order observer based control strategy. Considering a system of the form xx = x2 x2= x3 x3 = -5xx - 6x^ - 9x3 + xx (t - t)x2 (t - t) + u y = xx + x2 + 2 x3 Here x and x are assumed to be known states and x is assumed to be estimated using the proposed reduced order observer. System belongs to the class of uncertain nonlinear systems defined by (10) with n = 3 . The time delay t is taken as 1 sec. It is assumed that only output is available for measurement. The proposed observer controller strategy is applied to this system with an objective to solve the tracking problem of system. The desired trajectory is taken as yd = 0.5sin t + 0.1cos0.5t + 0.3 .Initial conditions are taken as x(0) = [0.6,0.2,0.5]r .Attenuation level for robust controller is taken as 0.01. Controller gain vector is taken as k = [10,5,1]. Wavelet networks with Mexican hat wavelet as the mother wavelet is used for approximating the unknown system dynamics. Wavelet parameters for these wavelet networks are tuned online using the proposed adaptation laws. Initial conditions for all the wavelet parameters are set to zero. Simulation results are shown in the figures. As observed from the figures, system response tracks the desired trajectory rapidly. Fig.3: Unknown and the Estimated States of the System 0.5 0 10 20 30 40 time(sec) Fig.4: Control effort and the Tracking error -0.5 -1 Fig.2: Known States of the System time(sec) Fig.5: Actual output, estimated output and output error A WNN reduced order observer based adaptive tracking control strategy is proposed for a class of systems with unknown system dynamics. Adaptive wavelet networks are used for approximating the unknown system dynamics. Adaptation laws are developed for online tuning of the wavelet parameters. The stability of the overall system is guaranteed by using the Lyapunov functional. The theoretical analysis is validated by the simulation results. Fig. 1 represents the states which are known in the system. As observed from the Fig. 2 that the unknown state is efficiently estimated by the proposed reduced order observer. Fig.3 indicates the control effort and the tracking error between the system output and desired output which converges rapidly. The plant output and the estimated output are shown in Fig. 5. Also the error between them is shown, which is of the order of10-5 which reveals the efficient observer design. A convergence pattern in the observer error is also reflected from the Fig. 3.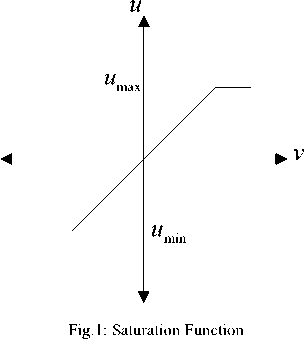
2.2 Fundamentals of Wavelet Neural Network
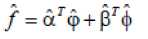
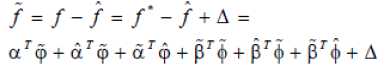
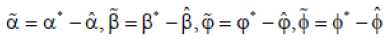
л =
^Ф1 _ dw
^(p2
’ dw '
’ dw _
У =
w=w
dw
d^, ’ dw ’
<," ’ dw _
w=w
^
d^2
^y
^_
d^
^m 1
"1 -
_ de
’ de ’
’ de _
c-c ■
de
de
’ de _
C-C
with
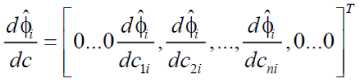
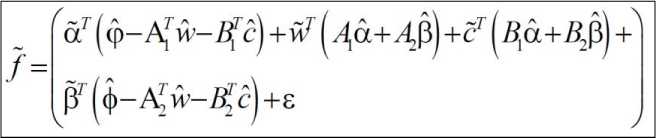
III. System Description
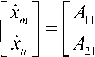
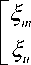
IV. Wavelet Reduced Order Observer Design
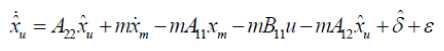
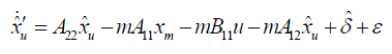
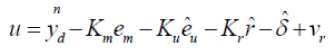
VI. Stability Analysis
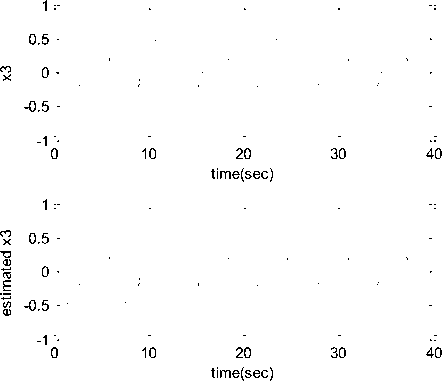


VIII. Conclusion
Список литературы Wavelet Adaptive Reduced Order Observer Based Tracking Control for a Class of Uncertain Time Delay Nonlinear Systems Subjected to Actuator Saturation
- H. Lens and J. Adamy, “Observer based controller design for linear systems with input constraints”, Proceedings of 17th World Congress, The international federation of automatic control, Seoul Korea, pp.9916-9921, July 2008.
- F. Abdollahi, H.A Talebi and R.V. Patel, “A stable neural network-based observer with application to flexible-joint manipulators”, IEEE Transactions on Neural Networks, Vol. 17, Issue 1, pp.118-129 Jan. 2006.
- M. Sharma, A. Kulkarni and A. Verma, “Wavelet Adaptive Observer Based Control for a Class of Uncertain Time Delay Nonlinear Systems with Input Constraints”, IEEE International Conference on Advances in Recent Technologies in Communication and Computing, ARTCOM, pp.863-86, 2009.
- V. Sundarapandian, “Reduced order observer design for nonlinear systems” Applied Mathematics Letters 19, pp. 936–941, 2006.
- Z. F. Lai and D. X. Hao, “The Design of Reduced-order Observer for Systems with Monotone Nonlinearities”, ACTA Automatica Sinica, Vol. 33, no.2, pp. 1290-1293, 2007.
- Y. G. Liu and J. F. Zhang, “Reduced-order observer-based control design for nonlinear stochastic systems”, Systems & Control Letters 52, pp. 123 – 135, 2004.
- G. Bartolini, E. Punta and T. Zolezzi, “Reduced-Order Observer for Sliding Mode Control of Nonlinear Non-Affine Systems”, Proceedings of the 47th IEEE Conference on Decision and Control, Mexico, 2008.
- J.P. Richard, “Time delay systems: an overview of some recent advances and open problems”, Automatica, vol. 39, pp. 1667-1694, 2003.
- E. Fridman and U. Shaked, “An improved stabilization method for linear time delay systems”, IEEE Transactions on Automatic Control, vol. 47, pp. 1931–1937, 2002.
- V.L. Khantonov and A.P. Zhabko, “Lyapunov-Krasovskii approach to robust stability analysis of time delay systems”, Automatica, vol. 39, pp. 15-20, 2003.
- F. Morabito, A. R. Teel, and L. Zaccarian, “Nonlinear antiwindup applied to Euler–Lagrange systems,” IEEE Transactions on Robotics and Automation, Vol. 20, no. 3, pp. 526-537, June 2004.
- P. He and S. Jagannathan, “Reinforcement learning neural-network-based controller for nonlinear discrete-time systems with input constraints,” IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, Vol. 37, no. 2, pp.425-436, April 2007.
- J. Zhou, M. Joo and Y. Zhou, “Adaptive neural network control of uncertain nonlinear system in presence of input saturation”, Proceedings of the ICARCV, pp.895-899, 2006.
- Q. Zhang and A. Benveniste, “Wavelet networks,” IEEE Transactions on Neural Networks, Vol. 3, no. 6, pp.889-898, November 1992.
- J. Zhang, G. G. Walter, Y. Miao, and. W. Lee, “Wavelet neural networks for function learning,” IEEE Transactions on Signal Processing, Vol. 43, no. 6, pp.1485-1497, June 1995.
- B. Delyon, A. Juditsky, and A. Benveniste, “Accuracy analysis for wavelet approximations,” IEEE Transactions on Neural Networks, Vol. 6, no. 2, pp.332-348 March 1995.

