Wavelet Neural Network Observer Based Adaptive Tracking Control for a Class of Uncertain Nonlinear Delayed Systems Using Reinforcement Learning
Автор: Manish Sharma, Ajay Verma
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 2 vol.4, 2012 года.
Бесплатный доступ
This paper is concerned with the observer designing problem for a class of uncertain delayed nonlinear systems using reinforcement learning. Reinforcement learning is used via two Wavelet Neural networks (WNN), critic WNN and action WNN, which are combined to form an adaptive WNN controller. The “strategic” utility function is approximated by the critic WNN and is minimized by the action WNN. Adaptation laws are developed for the online tuning of wavelets parameters. By Lyapunov approach, the uniformly ultimate boundedness of the closed-loop tracking error is verified. Finally, a simulation example is shown to verify the effectiveness and performance of the proposed method.
Wavelet neural networks, adaptive control, optimal control, reinforcement learning, Lyapunov- Krasovskii functional.
Короткий адрес: https://sciup.org/15010097
IDR: 15010097
Текст научной статьи Wavelet Neural Network Observer Based Adaptive Tracking Control for a Class of Uncertain Nonlinear Delayed Systems Using Reinforcement Learning
Published Online March 2012 in MECS
In many practical systems, the system model always contains some uncertain elements; these uncertainties may be due to additive unknown internal or external noise, environmental influence, nonlinearities such as hysteresis or friction, poor plant knowledge, reduced-order models, and uncertain or slowly varying parameters. Hence, the state observer for the uncertain system will be useful and apply to reconstruct the states of a dynamic system. The means to design adaptive observers through estimation of states and parameters in linear and nonlinear systems has been actively studied in recent years [1-3].Adaptive observers of nonlinear systems have attracted much attention due to their wide uses in theory and practice.
The phenomenon of time-delay exists in various engineering systems such as chemical process, long transmission lines in pneumatic systems, etc. Time-delay usually leads to unsatisfactory performances and is frequently a source of instability. Recently, much effort has been devoted to design the observer or observerbased control of time delay systems [4-6].
Reinforcement learning (RL) is a class of algorithms for solving multi-step, sequential decision problems by finding a policy for choosing sequences of actions that optimize the sum of some performance criterion over time[7-9]. In RL problems, an agent interacts with an unknown environment. At each time step, the agent observes the state, takes an action, and receives a reward. The goal of the agent is to learn a policy (i.e., a mapping from states to actions) that maximizes the long-term return. Actor-Critic algorithm is an implementation of RL which has separate structures for perception (critic) and action (actor) [10-12]. Given a specific state, the actor decides what action to take and the critic evaluates the outcome of the action in terms of future reward (goal).
Recently, wavelet neural networks (WNNs), which absorbs the advantages such as the multi-resolution of wavelets and the learning of NN, were proposed to guarantee the good convergence and were used to identify and control nonlinear systems [13-15].Wavelet networks are feed-forward neural networks using wavelets as activation function. The WNN is suitable for the approximation of unknown nonlinear functions with local nonlinearities and fast variations because of its intrinsic properties of finite support and self-similarity.
Incorporating the advantages of WNN, adaptive actorcritic WNN-based control has emerged as a promising approach for the nonlinear systems. A reinforcement signal is used to evaluate the performance of a computational agent interacting with its environment. The aim is to discover a policy for selecting actions that minimize a specified performance index. Reinforcement learning methods are considered potentially useful to feedback control systems since these methods do not require comprehensive information about the system or its behaviour. During supervised learning with a neural network as the computational agent, the weights are adjusted in proportion to the output error of the neurons.
Something different occurs when using reinforcement learning – the weights are adjusted according to the reinforcement signal. This is especially useful since no desired output signals are available online to train a neural controller. The general idea of reinforcement learning is extended to neural networks using an adaptive critic model. In the actor-critic WNN based control; a long-term as well as short-term system-performance measure can be optimized. While the role of the actor is to select actions, the role of the critic is to evaluate the performance of the actor. This evaluation is used to provide the actor with a signal that allows it to improve its performance, typically by updating its parameters along an estimate of the gradient of some measure of performance, with respect to the actor's parameters. The critic WNN approximates a certain “strategic” utility function that is similar to a standard Bellman equation, which is taken as the long-term performance measure of the system. The weights of action WNN are tuned online by both the critic WNN signal and the filtered tracking error. It minimizes the strategic utility function and uncertain system dynamic estimation errors so that the optimal control signal can be generated. This optimal action NN control signal combined with an additional outer-loop conventional control signal is applied as the overall control input to the nonlinear system. The outer loop conventional signal allows the action and critic NNs to learn online while making the system stable. This conventional signal that uses the tracking error is viewed as the “supervisory” signal [7].
These motivate us to consider the designing of WNN observer based adaptive tracking controller for a class of uncertain delayed nonlinear systems using reinforcement learning. WNN are used for approximating the system uncertainty as well as to optimize the performance of the control strategy. The actor critic architecture based WNN is shown in figure 3.
The paper is organized as follows: section II deals with the system preliminaries, system description is given in section III. Section IV describes the wavelet observer design. WNN based controller designing aspects are discussed in section V. Section VI deals with the tuning algorithm for actor-critic wavelets. The stability analysis of the proposed control scheme and the observer is given in section VII. Effectiveness of the proposed strategy is illustrated through an example in section VIII while section IX concludes the paper.
-
II. S YSTEM P RELIMINARIES
A.Wavelet Neural Network
Wavelet network is a type of building block for function approximation. It is a single layer network consisting of translated and dilated versions of orthonormal father and mother wavelet function. Basis functions are used in wavelet network span L2(^) subspace. Due to its universal approximation property any function f (x) e L2(^) can be approximated by linear combination of basis functions. The building block is obtained by translating and dilating the mother wavelet function. Corresponding to certain countable family ofa and b , wavelet function can be expressed as
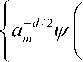
x—— |: m e Z, n e Zd am )
Considering m - m dd
am = a0 ,bn = na0 b0,m e Z,n e Z
The wavelet in (1) can be expressed as
Vmn ={a-m'2 V(a-mx - nb0 ) : m e Z, n e Zd }
( 1 )
( 2 )
Where the scalar parameters a and b define the step size of dilation and translation discretizations (typically a 0 = 2 and b0 = 1) and x = [ x , x 2,..., xn ] 7 e Rn is the input vector.
Output of an n dimensional WNN with m wavelet nodes is f = V V ОС Щ
J j mnr mn meZneZd
( 3 )
B.System Dscription
Consider a nonlinear system of the form x = x2
x 2 = x 3
x n = f [ x ( t ), x ( t - 0] + gu
y = x1
where x = [x,x2,...,xn]r ,u,y are state variable, control input and output respectively. т is the known delay in the state. f = [f,f,...,f]7 : ^n+1 ^^n are smooth unknown, nonlinear functions of state variables.
Rewriting the system (4) as x = Ax + B (f [ x (t), x (t - т) + gu ])
( 5 )
У = Cx where " 0
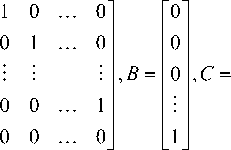
[ 10 0 0 ]
A =
The objective is to formulate a state feedback control law to achieve the desired tracking performance. The asymptotic tracking problem entails making a nonlinear system asymptotically track a desired reference trajectory while guaranteeing boundedness of all the internal variables. In its general formulation, even when the state of the plant is known, the tracking problem is considerably more difficult than that of stabilization. The main reason for its complexity lies in the fact that, even when the uncontrolled plant is an autonomous system, in order for the output to track the reference trajectory the controller should create and stabilize a time-varying equilibrium point in the closed-loop system which, in general, is difficult to calculate. The control law is formulated using the transformed system (5). Let n-1
Уа = [ Уа , Уа ,•••, Уа ] be the vector of desired tracking trajectory. Following assumptions are taken for the systems under consideration.
Assumption A1
-
a) Desired trajectory yd ( t ) is assumed to be smooth, continuous Cn and available for measurement.
-
b) For the system under consideration only output y is measurable.
III. W AVELET O BSERVER D ESIGN
Wavelet based observer that estimates the states of the system (5) is given by
^ = Ax + BVfXW),x Assumption A2 . Ц/^), x(t - r))- /(f(t), Hr - r))|| < у ||f || + y2 ||f (,- r)|| a) V. ADAPTIVE WNN CONTROLLER DESIGN A novel strategic utility function is defined as the longterm performance measure for the system. It is approximated by the WNN critic signal. The action WNN signal is constructed to minimize this strategic utility function by using a quadratic optimization function. The critic WNN and action WNN weight tuning laws are derived. Stability analysis using the Lyapunov direct method is carried out for the closed-loop system (5) with novel weight tuning updates. A.Strategic Utility Function The utility function p(k) = [p. (k)]”t e ^m is defined on the basis of the filtered tracking error rˆ and is given by: p,(k) = 0 if r^ < n (10) =1 if r2> n where p(k) e^,i' = 1,2,...,m and n e^ is the predefined threshold. p(k) can be considered as the current performance index defining good tracking performance for p(k) = 0 and poor tracking performance for p(k) = 1 . The strategic utility function Q‘(k) e ^m can be defined using the binary utility function as b) For a symmetric positive definite matrix Q there exist a symmetric positive definite matrix P such that (A -mC)TP+P(A - mC) = -Q and (PB)T = C where x = x-5c is the state variable estimation error while y and Y are positive constants. Defining the error system as х=(А-/иОх^ШИ ( 7 ) y = Q The robust control term is defined as Q'(k) = aNp (k +1) + aN-1 p (k + 2) +...+a+1 p (N) +... where ae^ and 0<a<1 and N is the horizon. Above equation may be rewritten as Q(k) = minu (k ){«Q(k -1) -aN+1p(k)} (12) B.Critic WNN vr У (p2+1) 2p2 (8) where p is the prescribed attenuation. The long term system performance can be approximated by the critic WNN by defining the prediction error as , ec(k) = Q(k)-a(e(k-l)-a№p(k)) where Q(k)= ^ккЖ\тхх<к^=СалкШк^ IV. BASIC CONTROLLER DESIGN USING FILTERED TRACKING ERROR Defining the state tracking error vector eˆ(t) as The filter tracking error is defined as where K = [kpk2,.. k-,,1] is an appropriately chosen coefficient vector such that e > 0 exponentially as ^ > 0. Applying the feedback linearization method, the control law is defined as w = — (vd-k(f(x(t\x(t-T)) + mCx^ Kee-krr) ( ^ ) g ' whereKe = [0,k1,k2,...,kn-1 ] . ec(k) e^m , QQ(k) e^m is the critic signal , wx(k) e^n1 xm and v e^nmxn1 represent the weight estimates, ф(k) e^n1 is the wavelet activation function and n is the number of nodes in the wavelet layer. The objective function to be minimized by the critic NN is defined as: Ec (k) = - ecT (k) ec (k ) (14) The weight update rule for the critic NN is derived from gradient-based adaptation, which is given by where Afr1 (k) = a Or dEc (k) d wx( k) и^ +1) = ^(А:)-^^) where а g^ is the WNN adaptation gain. The critic WNN weights are tuned by the reinforcement learning signal and the discounted past output values of critic WNN. f (x(k)) is unknown. However, using (9), the functional estimation error is given by f (k) = r - r + 5( k) (25) C.Action WNN The action NN is implemented for the approximation of the unknown nonlinear function f (x(k)) and to provide an optimal control signal to the overall input u(k)as Substituting (25) in to (24) ,we get iv2 (A +1) = w2(A) - а2ф2(кXQ(k) + r- г + ^'(A) f To implement the weight update rule, the unknown but bounded disturbance 5(k) is taken to be zero. Then, (25) /(A)= ^(А)^(р^л(А))= ^(A)^(A) (17) where W2(k) g^n2xm and v2 g^nmxn2 represent the matrix of weight estimate, ф (k) g^n2 is the activation function, n is the number of nodes in the hidden layer. Suppose that the unknown target output-layer weight for the action WNN is w then we have f(k) = WT(kЖ(VTX(k))^2 (x(k)) = WT(k)ф2 (k)8(x(k)) (18) where 82(x(k)) g^m is the WNN approximation error. From (17) and (18), we get f (k) = f (k) - f (k) = (W2(k) - W2)Tф2(k) — 82(x(k)) ( 19) where f (k) g ^m is the functional estimation error. The action WNN weights are tuned by using the functional estimation error f(k)and the error between the desired strategic utility function Qd (k) g^m and the critic is rewritten as Coincidentally, after replacing the functional approximation error, the weight update for the action NN is tuned by the critic WNN output, current filtered tracking error, and a conventional outer-loop signal. The block diagram of the overall closed loop system using actor critic WNN based observer is shown in figure 4. VI. STABILITY ANALYSIS Consider a Lyapunov-Krasovskii functional of the form V =1xTPx +1r2+ t J w(o)da t-T (27) Differentiating it along the trajectories of the system V = -^xTQ5 + xrPB(5(\. yri)- £(.f, yrf)- V,) + xTP(0(.xUY x(t - t))- ф(хй\ x(t - r))) +r(Ke? + К(ф(х(Г \x(t - г)) + mCxi + ^(.i, yd) signal Qˆ (k). Define ea (k) = f (k) + (Q (k) - Qd (k)) (20) The objective is to make the utility function Q(k)zero at every step. Thus (20) becomes ea (k) = f (k) + Q (k) (21) The objective function to be minimized by the action NN is given by +gv+ г, - у\)+ w(x(A))- wUCf-r)) Substituting control law v in the above equation = —16mi„ ||.r || + vrPB(6(x, yd ) - 3(x, >d)+3(x, yd) - vr) + xTP(0(x(t), x(t - r)) - ^(i(r), X(t - r))) + r(vr - kr f >+ w(jc(f))-w(jr(r-r)) s4q^H+mj|<+«,II<*«,MH^ +xT PB(3(x, yd) - vr) + M4 + r(,-k,r) + И'(х(г)) - w^t - r)) Ea (k) = 2 eT (k) ea (k) The weight update rule for the action NN gradient based adaptation, which is defined as (22) is also a M1 =1 lPSl |Г3,M2 = PmaxYl,M3 = Pmax/2,M4 = max |rvr| +У4 и^(^ + I) = %(A) + Aiv2(A) (23) where AW2 (k) = а 6Ea ( k) — Sw2 (k) or % (A +1) = %(A) - агфг (кXQ(k)+Дк V (24) where a g^ is the WNN adaptation gain. The WNN weight updating rule in (24) where /1,/2,/3,У4 ^ 0 Substituting the robust control term in above equation, ^ -1 Qmin ||x2 11 + M1 IIxlI' + M2 IIxlI' + M3 IIxllllx(t - T)|| o2 , y2 . + 828 -^ + M^ - k^2 + w(x(t)) - w(x(t - t)) Applying Young’s inequality in the fourth term of the above equation, M31 |x| ||x (t - t)|| < M3^ ||x| p+M2-1 x (t - t)||2 cannot be implemented in practice since the nonlinear function Selecting w(x(t)) = M3 2 x results in ^ -1 Qm,n ||X2 11 + (M1 +M2 +M3^- +M^) ||X||2 ц +—e\ -— + M4 - krrг 2 5 2 4 r The system is stable as long as krr2 + у + 1 Qmin |X2|| ^ (M1 + M2 + '^ + MT)lИ2 2 2"" 2 2ц +—e \ + M. 2 5 4 (28) VII. SIMULATION RESULTS Figure 2. Tracking error, Observer error and control effort Simulation is performed to verify the effectiveness of proposed reinforcement learning WNN observer based control strategy. Considering a system of the form VIII. CONCLUSION И1 = X2(t) x2= xt (t) xt (t - t) x2 (t - t) sin x2 + u (29) y = X1 System belongs to the class of uncertain nonlinear systems defined by (4) with n = 2. The time delay т is taken as 1 sec. It is assumed that only output is available for measurement. The proposed observer controller strategy is applied to this system with an objective to solve the tracking problem of system. The desired trajectory is taken as yd = 0.5sint + 0.1cos0.5t + 0.3.Initial conditions are taken as x (0) = [0.75,0]^ .Attenuation levels for robust controller are taken as 0.01. Controller gain vector is taken as k = [25,3]. Wavelet networks with discrete Shannon’s wavelet as the mother wavelet is used for approximating the unknown system dynamics. Wavelet parameters for these wavelet networks are tuned online using the proposed adaptation laws . Initial conditions for all the wavelet parameters are set to zero. Simulation results are shown in the figure. As observed from the figures, system response tracks the desired trajectory rapidly. Figure 1. System output. Observer output and desired trajectory A reinforcement learning WNN observer based adaptive tracking control strategy is proposed for a class of systems with unknown system dynamics. Adaptive wavelet networks are used for approximating the unknown system dynamics. Adaptation laws are developed for online tuning of the wavelet parameters. The stability of the overall system is guaranteed by using the Lyapunov functional. The theoretical analysis is validated by the simulation results. As observed from the figure 2 that tracking error rapidly converges to the small value of the order of 10-6. A convergence pattern in the observer error is also reflected from the figure.
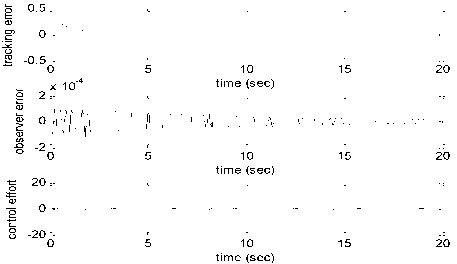
Список литературы Wavelet Neural Network Observer Based Adaptive Tracking Control for a Class of Uncertain Nonlinear Delayed Systems Using Reinforcement Learning
- H. Lens and J. Adamy, “Observer based controller design for linear systems with input constraints”, Proceedings of 17th World Congress, The international federation of automatic control, Seoul Korea, pp.9916-9921, July 2008.
- F. Abdollahi, H.A Talebi and R.V. Patel, “A stable neural network-based observer with application to flexible-joint manipulators”, IEEE Transactions on Neural Networks, Vol. 17, Issue 1, , pp.118-129 Jan. 2006.
- F. Sun; Z. Sun; P. Y. Woo, “Neural network-based adaptive controller design of robotic manipulators with an observer”, IEEE Transactions on Neural Networks, Vol. 12, Issue 1, pp.54-67 Jan. 2001.
- M. S. Mahmoud, Y. Shi and H. Nounou, “Resilient observer based control of uncertain time delay systems”, International journal of Innovative Computing, Information and Control, Vol. 3 no.2, pp.407-418.Apr.2007.
- P. Cui and C. Zhang, “Observer design and output feedback stabilization of linear singular time delay systems with unknown inputs”. Journal of control theory application, Vol. 6, no.2, pp-177-183.Apr.2008.
- J.P. Richard, “Time delay systems: an overview of some recent advances and open problems”, Automatica, Vol. 39, pp. 1667-1694, 2003.
- P. He and S. Jagannathan, “Reinforcement learning neural-network-based controller for nonlinear discrete-time systems with input constraints,” IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, Vol. 37, no. 2, pp.425-436, April 2007.
- W.S. Lin, L.H. Chang and P.C. Yang, “Adaptive critic anti-slip control of wheeled autonomous robot”, IET Control Theory Applications, Vol. 1, No. 1, January 2007.
- X. Lin and S. N. Balakrishnan, “Convergence analysis of adaptive critic based optimal control,” Proceedings of the American Control Conferenc, pp. 1929–1933, 2000.
- D. V. Prokhorov and D. C. Wunsch, “Adaptive critic designs”, IEEE Transactions on Neural Networks,, vol. 8, no. 5, pp. 997–1007, Sep. 1997.
- H. V. Hasselt and M. Wiering, “Reinforcement learning in continuous action spaces”, IEEE Symposium on Approximate Dynamic Programming and Reinforcement Learning, pages 272–279, 2007.
- Hussein Jaddu and Kunihiko Hiraishi, “A Wavelet Approach for Solving linear quadratic optimal control problems”, SICE-ICASE International Joint Conference ,Oct. 18-21, Korea, 2006.
- Q. Zhang and A. Benveniste, “Wavelet networks,” IEEE Transactions on Neural Networks, Vol. 3, no. 6, pp.889-898, November 1992.
- J. Zhang, G. G. Walter, Y. Miao, and. W. Lee, “Wavelet neural networks for function learning,” IEEE Transactions on Signal Processing, Vol. 43, no. 6, pp.1485-1497, June 1995.
- B. Delyon, A. Juditsky, and A. Benveniste, “Accuracy analysis for wavelet approximations,” IEEE Transactions on Neural Networks, Vol. 6, no. 2, pp.332-348 March 1995.

