Задача быстродействия при моделировании саккадического движения глаза
Автор: Кручинина А.П.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (87) т.24, 2020 года.
Бесплатный доступ
В данной статье обсуждается вопрос изучения быстрых целенаправленных движений глаз человека. Такие движения моделируются различными способами. Один из них - решение оптимальных задач. В предлагаемой работе рассматривается быстрое одиночное согласованное баллистическое движение глаз - саккада. Результатом решения задачи быстродействия является уравнение движения глаза на саккаде. Система уравнений, описывающая движение глазного яблока и прилагаемого к нему со стороны глазодвигательной системы управляющего момента, основана на маятниковой модели. Особенность данной системы: все вводимые величины имеют физический смысл и выбраны на основе результатов опубликованных исследований. Ее основное отличие от имеющихся работ заключается в учете ограниченности скорости изменения управляющего момента, развиваемого парой глазодвигательных мышц. В этом случае разомкнутая система имеет два действительных корня и один нулевой. В статье проанализирован случай соотношения - частный случай соотношения действительных корней 1:3. В результате моделирования получены траектории, по своим характеристикам приближенные к наблюдаемым в экспериментальных исследованиях саккадам. На основе построенной модели проведено сравнение параметров синтезированных саккад с параметрами, полученными на экспериментальной выборке. Полученные модели могут использоваться как для задач физиологии и медицины, так и при построении сред виртуальной реальности. Например, при разработке пространственных интерфейсов использование математической модели позволяет оптимизировать расположение элементов путем применения теории игр.
Саккада, движение глаз, задача быстродействия, оптимальное управление, ограничение на скорость сокращения мышцы, моделирование движения, глазодвигательный аппарат
Короткий адрес: https://sciup.org/146282157
IDR: 146282157 | УДК: 531: | DOI: 10.15593/RZhBiomeh/2020.1.04
Текст научной статьи Задача быстродействия при моделировании саккадического движения глаза
Быстрые движения глаз человека относятся к наиболее сложным для изучения движениям в силу своей высокой скорости и труднодоступного для наблюдения расположения глазодвигательного аппарата. Тем не менее за последние десятилетия накоплен значительный экспериментальный и теоретический материал о движении глаз. Его осмысление и описание математическими моделями сегодня востребовано при создании тренажеров, имерсивных компьютерных сред и применении технологий виртуальной реальности, разработке и тестировании интерфейсов виртуальной реальности. При создании пространственного интерактивного интерфейса требования к его визуальной части возрастают. Процесс тестирования и настройки параметров
Кручинина Анна Павловна, ассистент кафедры прикладной механики и управления, Москва предлагается оптимизировать, применив симуляционные среды [10]. При подобном моделировании движения глаз человека можно имитировать, используя различные модели глазодвигательной системы и управления ею. При выборе математического описания одним из факторов является его чувствительность к возмущениям. В работе предложено моделирование быстрого движения глаза с использованием решения задачи быстродействия и проанализировано влияние возмущений в начальных условиях на траектории решения задачи.
В литературе опубликованы математические модели одиночных саккадических движений глаз [9]. Описание одиночной саккады в результате решения задачи быстродействия приведено в работе [4]. Однако эти работы не описывают некоторых существенных особенностей движения глаза. В частности, математические модели не описывают пре- и постсаккадические движения, описанные в работах [5, 7].
Анализ подобных особенностей движения глаз применяется в исследованиях высшей нервной деятельности человека, функционирования мозга и т.д. В связи с этим дальнейшее исследование задач моделирования представляет интерес.
Модель глаза и глазодвигательного аппарата и ее формализация
Составим упрощенную модель, в которой глаз описывается твердым шаром. Учтем наличие сил вязкого сопротивления и силы упругости, действующей со стороны глазодвигательных мышц, глазного нерва и окружающих тканей. Считается, что вращение происходит вокруг геометрического центра шара. Оптический̆ центр вращения глаза находится на расстоянии около 13 мм от передней вершины роговицы [12], и его можно считать неподвижным.
Рассмотрим движение глаза в горизонтальной плоскости. Необходимо отметить, что термин «горизонтальная плоскость» условен и означает движение, реализуемое парой внешней и внутренней прямых мышц.
Будем описывать глаз и глазодвигательную систему следующим уравнением:
I ϕ+υ R ϕ+ kR ϕ= M , (1)
где I – момент инерции глаза I =4,6⋅10-7 кг·м2; ϕ – угол пововорота глаза, υ и k – коэффициенты вязкости и упругости соответственно, υ = 0,0023 Н·c/м и k = 0,0043 Н/м; R – радиус глаза, R = 12 мм, и M – управляющая составляющая момента горизонтальной пары глазодвигательных мышц. Сокращение и расслабление мышц данной пары, как и всех скелетных мышц, происходит за характерные времена, оцениваемые по данным работы [11], 10 мс. Максимальное усилие, развиваемое глазодвигательными мышцами, составляет 0,4 H [13]. В соответствии с этими данными ограничение на скорость изменения величины M положим равным 0,04 H/с, так как значение момента | M - υRϕ - kRϕ | ≤ 0,4 H·м/с. Опишем изменение момента M дифференциальным уравнением dM dt
где U – скорость изменения величины M . Таким образом, к уравнениям (1) и (2) добавляется ограничение
U ≤ U *.
Задача быстродействия
Задача, решаемая при помощи движения глаз, - максимизация времени, когда на сетчатке формируется четкое изображение. Исследование параметров четкого видения было проведено еще в прошлом веке, например, в работе [8]. Характерные значения отклонения и скорости движения изображения объекта по сетчатке глаза не должны превышать 2° и 4°/с соответственно. Следовательно, время, когда эти условия нарушаются, должно быть минимально.
Рассмотрим задачу перевода взора с одного объекта на другой, т.е. наискорейшего поворота глазного яблока из положения покоя (ф(0) = 0, ф (0) = 0 ) на угол ф ( Т ) = ф, , с нулевой угловой скоростью в конечный момент времени ф(Т ) = 0. Известно, что на момент начала движения момент М имеет порядок 10-20% от максимального. Не нарушая общности рассуждения, будем считать, что саккада начинается из положения, при котором M (0) = 0. Значение момента в конце движения также определяется однозначно из требуемого угла поворота.
Объединяя уравнения (1)-(2) с начальными и конечными условиями, а также с ограничением (3), получим формальную систему для задачи оптимального быстродействия.
Решение задачи быстродействия
Изложим основные шаги решения этой задачи.
M
Проведем замену переменных xv = ф, x2 = ф, x3 = — и введем обозначения л 2vR . 2kR „ U „_______
A = , A = —, и = —. Приведем систему (1)-(2) к системе уравнений первого порядка:
X , = х 2,
X 2 = - A3xx - Ax 2 + х 3, X 3 = и .
Ограничения на управление и граничные условия примут вид
X (0) = x 2 (0) = x 3 (0) = 0, x i ( T ) = A t , x 2( T ) = 0,
I и |< и | |-- w тах ,
T ^ min.
u
Как и ранее, в выражениях (4)-(6) A - амплитуда саккады; Мт - момент силы, необходимый для фиксирования глаза в новом положении, Мт = - AA ; T -продолжительность саккады.
Решение задачи осуществляется с помощью принципа максимума Понтрягина [1]. Обозначим через вектор у = ( v , ф2, V) сопряженные переменные. Тогда функция Понтрягина записывается в форме
H = x2 Ж1 + (— Ax — Ax + X 3 )Ж2 + и Жз •
Максимальность функции Понтрягина достигается при управлении u = u maх sign Жз. Вид Жз определяется из сопряженной системы:
Ж 1 = A Ж 2 , Ж 2 = —Ж 1 + А1 Ж 2, Ж 3 = —Ж 2 .
(7*)
Условия трансверсальности имеют тривиальный вид и здесь выписываться не будут. Так как условие Ж; = 0 влечет тривиальное решение системы (7*), то управление представляет собой кусочно-разрывную функцию вида
u = 4
и m , 0 < 1 < t i (I),
— u m , t i < t < t 2 (II), U m, 1 2 < 1 < T (III),
где u = um„v или м = —u v. Можно показать, что u„ = —um„v не является решением m max m max m max задачи, поэтому рассмотрим случай um = umaх.
Римскими цифрами обозначим номера интервалов, моменты времени переключения и окончания саккады – неизвестны. Определим их исходя из условий на правом и на левом концах.
Обозначим С / постоянные в решении, здесь i = 1, 2, j = I, II, III, а через X. обозначим ненулевые собственные числа системы (4). В данном случае существует два действительных корня. Ряд подобных задач рассматривался в работах [2, 3], но случай с одним нулевым корнем остался нерассмотренным.
Решение на интервалах I, II и III примет вид
x 1 = C^e X 1 * + C I e X 2 1 + u^ — A 1 u m ,
x‘ = X, C^e " + X 2 C/e ' 1 + u m , 2 11 22 A
X3
11 = Xlt CII X21 _umL , 2um'1 , A1um xi e i e i I
1 1 2 A2 A2
x“ = X C
II e ^ 1 1 + X2 C“ e X 2 1
—
и m
A 2 ,
x 3 II
x"1 = C“Ie X1‘ + C"Ie'
= 2 u m t 1 — u m t ,
,X 2 1 + u m t + 2 u m ( t 1 — t 2 )
—
A 2
A 1 u m
A 2 2 ,
x™ =X. C™e ‘1' +X, C™e ^2' + u m ,
2 11 22 A x3 = u m1 + 2u m ('1 — 12 )•
Данную систему уравнений необходимо разрешить относительно неизвестных времен переключения tx, t2 и Т. Постоянные решения С/ (i = 1, 2, j = I, II, III) определяются из условий непрерывности и гладкости решения и граничных условий. Произведем замену nx = e\ n2 = e 2, n3 = er. Такая замена позволяет перейти к системе полиномиальных уравнений. Переменная n выражается следующим образом:
n3 = eMrn| n12
.
Особенность системы (4), описывающей движение глаза, заключается в том, что для собственных чисел справедливо соотношение Х2 ® 3Х[. Для полуаналитического решения примем, что равенство Х2 =3Х, выполняется. В этом случае замена х, переменных zx = n2 1
уравнений вида
и z
/ \ Х1
n2
V П 1 >
приводит к системе двух полиномиальных
f F ( z„ z 2 , Х 1 ) = 0, I
IF2(z1, z2, X1) = 0, где функции F (zx, z2, X,) и F (zx, z2, Xi) имеют вид
F ( Z 1 , z 2 , X 1 ) = D 1 z 3 + D 2 Z 1 z 4 + D 3 z 3 z 6 + D 4 z 9 - D 5 z 27 + D 6 z 2 6 ,
F ( z ., z7 , X.) = 3X. Dz 3 + 3X. Dz. z 4 + 3X. Dz 3 z 6 + Dz 9 — Dz 7 — Dz 6 .
2 1 2 1 1 11 1 21 2 1 31 2 72 82 92
Здесь коэффиценты D зависят исключительно от постоянных системы, начальных и конечных условий. Выражения этих коэффициентов громоздки, поскольку получаются при помощи пакетов символьных вычислений. Разность уравнений F ( z 1, z 2, X1) — F ( z 1, z 2, X1 )3X1 = 0 оказывается в силу X2 =3X, линейным уравнением относительно z . Тогда z выражается следующим образом:
.
Моделирование одиночного саккадического движения глаза
Параметры модели движения глаза выберем, используя физиологические данные [8], и = 0,0023 Н^с/м и к = 0,0043 Н/м. Проведем расчет траекторий по формуле (9).
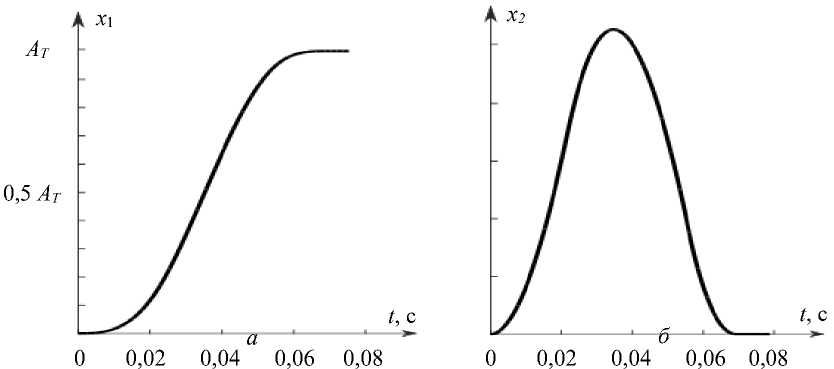
Рис. 1. Временная зависимость угла поворота глаза ( а ) и скорости поворота глаза ( б ) при нулевых начальных условиях
На рис. 1 показаны траектория глаза и график скорости при точном соответствии предполагаемых и реальных начальных условий.
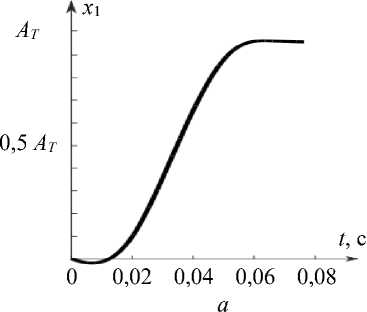
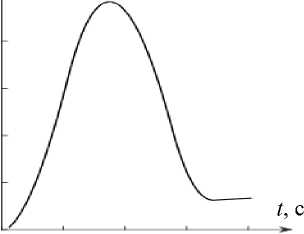
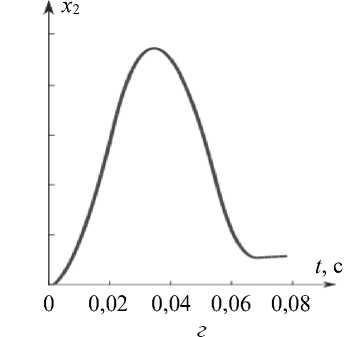
При рассматривании объекта глаз совершает микросаккады, т.е. разворачивается на малые углы. Фактические начальные условия отличаются от нейтральных. Рассмотрим ситуацию, когда присутствует отклонение от нуля в начальных условиях при сохранении вида управления. Проанализируем отклонения в начальных условиях по каждой из компонент вектора состояния. На рис. 2 приведены графики для случаев, когда % , (0) = 0, х 2 (0) < 0, х 3 (0) < 0 ( а, б ) и х , (0) = 0,1 A , хг (0) < 0, х 3 (0) < 0 ( в , г ).
При наличии подобных возмущений форма траектории меняется и можно говорить, что имеется траектория, схожая с наблюдаемой на экспериментальных записях. В работе [6] приведён способ аппроксимации экспериментальных записей гладкой функцией, и предложено несколько коэффициентов, описывающих форму саккады. Для сравнения теоретических результатов моделирования рассчитаем предложенные в работе [5] величины амплитуд пре- и постдвижений для модельных данных.
При возмущении в моменте или в начальной скорости получим, что пресаккада составляет 10% длительности и 10% продолжительности. Аналогичные параметры наблюдаются для саккад амплитудой 20–30 градусов [5, 6].
Таким образом модель оптимального управления, основанного на модели третьего порядка, позволяет описать появления пре- и постсаккад в результате управления, состоящего в решении задачи быстродействия при наличии возмущений в начальных условиях. Данное решение может использоваться для симуляции и моделирования перевода взора человеком с одной точки на другую. Такая задача возникает при проектировании и тестировании объемных интерактивных интерфейсов.
л x 2
0 0,02 0,04 0,06 0,08
б
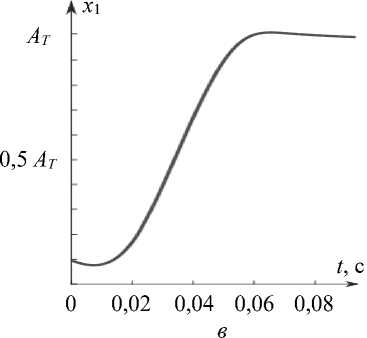
Рис. 2. Графики угла поворота глазного яблока и скорости при наличии отклонений в начальных условиях
Благодарности
Работа поддержана грантом РФФИ 18-00-01590.
P. 479–484.
Vol. 66. – P. 357–366.
Список литературы Задача быстродействия при моделировании саккадического движения глаза
- Александров В.В., Болтянский В.Г., Лемак С.С., Парусников Н.А., Тихомиров В.М. Оптимальное управление движением: учеб. пособие. - М.: Физматлит, 2005. - 376 с.
- Атанс М., Фалб П.Л. Оптимальное управление. - М.: Машиностроение, 1968. - 764 с.
- Кручинин П.А., Касаткин Е.А. Стабилометрический тест со ступенчатым воздействием и задача оптимального быстродействия // Изв. ЮФУ. Техн. науки. - 2014. - № 10. - C. 254-260.
- Кручинина А.П., Якушев А.Г. Математическая модель оптимального саккадического движения глаза, реализуемого парой мышц // Биофизика. - 2018. - Т. 63, № 2. - С. 334-341.
- Кручинина А.П., Якушев А.Г. Параметризация траектории саккадического движения глаза // Вестн. Моск. ун-та. - 2018. - № 2. - С. 68.
- Кручинина А.П., Якушев А.Г. Статистическое исследование форм одиночного саккадического движения глаза // Фундаментальная и прикладная математика. - 2018. - Т. 22, № 2. - С. 195-207.
- Araujo C., Kowler E., Pavel M. Eye movements during visual search: the costs of choosing the optimal path // Vision Research. - 2001. - Vol. 41. - P. 3613-3625.
- Burr D.C., Ross J. Contrast sensitivity at high velocities // Vision Research. - 1982. - Vol. 28. -P. 479-484.
- Happee R. Time optimality in the control of human movements // Biological Cybernetics. - 1992. -Vol. 66. - P. 357-366.
- Hôllerera T., Feinera S., Hallawaya D., Bella B., Lanzagortab M., Brownb D., Julierb S., Baillotb Y., Rosenblumb L. User interface management techniques for collaborative mobile augmented reality // Computers & Graphics. - 2001. - Vol. 25, no. 5. - P. 799-810.
- Marieb E., Hoehn K. Human anatomy and physiology. - San Francisco: Benjamin Cummings, 2010. - 8th edition. - 1114 p.
- Moore K.L., Dalley A.F., Agur A.M.R. Clinically oriented anatomy. - Baltimore: Wolters Kluwer, 2013. -7th ed. - 906 p.
- Pfann K.D., Keller E.L., Miller J.M. Muscle tension during unrestrained human eye movements // Annals of Biomedical Engineering. - 1995. - Vol. 23. - P. 346-358.


