Задача Конвея-Гордона для редуцированных полных пространственных графов

Настоящая работа посвящена исследованию редуцированных полных пространственных графов , то есть вложенных в R ³ графов, которые получаются из полных графов удалением нескольких рёбер, инцидентных одной вершине. Гамильтоновой парой циклов в пространственном графе называется пара непересекающихся простых замкнутых путей по его рёбрам, проходящим через все его вершины.

Пусть l ₁ ∪ l ₂ ⊂ R ³ – двухкомпонентное зацепление. Определим величину lk ₂( l ₁, l ₂) как остаток от деления на 2 коэффициента зацепления lk ( l ₁, l ₂) . Этот остаток не зависит от выбора ориентаций компонент l ₁ и l ₂ . Для каждого пространственного графа G определим значение функции ω ₂( G ) как остаток от деления на 2 суммы ∑ lk ₂( α , β ) , где суммирование берётся по всем га- ( α , β ) мильтоновым парам циклов ( α , β ) в графе G .

Изначально функция ω ₂ была предложена Дж. Конвеем и К. Гордоном для полных пространственных графов с шестью вершинами (см. [1]). Они использовали её для доказательства того, что каждый такой граф содержит нетривиальное зацепление. В работе [2] нами было показано, что значение функции ω ₂ для полного пространственного графа K _n , n ≥ 6 равно нулю тогда и только тогда, когда n ≥ 7 . Помимо этого в работе [3] нами было показано, что значение функции ω ₂ равно нулю для всех полных двудольных пространственных графов. Также в работе [4] показано, что значение функции ω ₂ равно единице для всех пространственных графов из семейства Петерсена.

В настоящей работе мы вычисляем значение функции ω ₂ для всех редуцированных полных пространственных графов, которые получаются из полного пространственного графа с n ≥ 8 вершинами удалением m рёбер, 0 <  m <  n - 2, инцидентных одной вершине. Оказывается, что для всех таких графов значение функции ω ₂ равно нулю. Доказательство состоит из двух шагов: сначала мы показываем, что значение функции ω ₂ не зависит от вложения графа в R ³ . Затем мы доказываем тривиальность функции ω ₂ , используя каноническое вложение полного графа в R ³ (также оно использовалось в [2, 5]).

1.    Независимость функции го2 от вложения

Далее через G n _m будем обозначать пространственный граф, который получается из полного графа с n вершинами удалением m рёбер, инцидентных одной вершине, V ( G n _m ) - множество вершин этого графа, E ( G _{n m} ) - множество его рёбер, Г ( G n _m ) - множество гамильтоновых пар циклов в графе G _{n m} . Пусть a , b е E ( G _{n m} ). Обозначим L _ab ( G _{n m} ) множество гамильтоновых пар циклов в графе G _{n m} , одна из компонент которых проходит по ребру a , а другая - по ребру b .

Теорема 1. Пусть G _nm - редуцированный полный пространственный граф, n >  8, 0 <  m <  n - 2. Тогда для любых двух рёбер a , b е E ( G _nm ) мощность | L ab ( G _nm )| чётна.

Доказательство. Пусть v . , - , v _n е V ( G n _m ) - вершины графа G _nm , и пусть этот граф получается из полного пространственного графа удалением m рёбер, инцидентных вершине v . . Обозначим A s с L ab ( G n _m ), s = 3,4, множество, состоящее из гамильтоновых пар циклов, в которых найдётся компонента, являющаяся s -угольником и проходящая по ребру a и через вершину v . . Можно считать, что если ( а , в ) е A s , то компонента а удовлетворяет этому условию. Заметим, что для каждой такой компоненты а пары циклов ( а , в ) е A s существует ровно ( n - 5)! различных компонент в , если а - треугольник, и ровно ( n - 6)! различных компонент в , если а -четырёхугольник. Следовательно, так как n >  8, то множества A 3 и А ₄ чётны. Аналогичным образом чётными являются множества B s с L ab ( G _nm ), s = 3,4, состоящие из пар циклов, в которых найдётся компонента, являющаяся s -угольником и проходящая по ребру b и через вершину v . .

Так как множества A₃, A ₄, B 3 и B ₄ попарно не пересекаются, то для доказательства чётности множества L ( G ) достаточно показать, что множество a , b n , fm

"М^ ) = L a , b ( G n , m ) \ ( A 3 U A 4 U B 3 U в 4 )

чётно. Для этого каждой паре циклов (а, в) е Lab (Gnm) сопоставим другую пару циклов (а',/П е La,b (Gn,m ) . Пусть а = (vl. , v2 , v3,-, vk ) и в = (vj. , vj 2, vj3,-, vj, ) .

Такая запись означает, что компонента а образована последовательным обходом вершин v . p v 1 ₂ , v i ₃ , - , v i k е V ( G _nm ), а компонента в образована последовательным обходом вершин v j . , v j ₂ , v j ₃ , - , v j / е V ( G _nm ), где k + / = n и k , I > 3. Без ограничения общности можно считать, что ребро a е E ( G _nm ) инцидентно вершинам v . ,v i 2 , а ребро b е E ( G _nm ) инцидентно вершинам j v j 2 .

Рассмотрим два случая.

Случай 1. Пусть ( а , в ) е L ab ( G _nm ) , причём компонента а проходит через вершину v . и v . ё { v i . , v i 2 , v i ₃ , v, }. В этом случае построим новую пару циклов ( а ¹, в ') с помощью операции переключения :

^а ' =⁽ v p v., v j 3 , - , v j / ) ^{и в} ' =⁽ j v j 2 , ^v ^ , - , v )•

Так как максимальный подграф графа G _nm , натянутый на вершины v ₂, - , v n , является полным, значит он содержит рёбра, соединяющие пары вершин ( v i 2 , v j -3 ),( v i . , v j l ),( v j -2 , v i ₃ ) и ( v j . , v i k ). Непосредственно проверяется, что так как n >  5, то ( а ¹, в ') е L _a , _b ( G n , m ) и пары ( а ¹, в ') и ( а , в ) различны.

Математика

Случай 2. Пусть теперь компонента а пары ( а , в ) е L ab ( G n _m ) проходит через вершину v 1 и v 1 = v, , где s е {1,2,3, к }. С точностью до переобозначений можно считать, что v 1 = v i 2 или v 1 = v i 3 . В этом случае также с помощью переключения построим новую пару ( а ', в ')е М^г ) :

^а ' = ⁽ v i , ^v 2 , v i 3 , v i 4 , v j 3 , - , j ) ^{и в} = ⁽ j v j 2 , v S ’ - ’ ^v k ).

Непосредственно проверяется, что ( а ¹, в ') е L a , _b ( G n , _m ) и пары ( а ¹, в ') и ( а , в ) различны.

Аналогичным образом рассматривается случай, когда компонента в пары (а, в) е La,ь (Gn,m) проходит через вершину v1 и v1 = vj, где s е {1,2,3, I}, I > S. Таким образом, всё множество La,ь (Gn,m) разбито на пары, следовательно оно является чётным. Тогда чётным является и множество La,ъ (Gn,m). Теорема 1 доказана.

Следствие 1. Пусть G n , _m и G ' n , _m - два редуцированных полных пространственных графа, n >  8, 0 <  m <  n - 2. Тогда m ( G n , m ) = « г ( G ' n , m )•

Доказательство. Пространственный граф G ' _n , _m получается из пространственного графа

G n , _m с помощью изотопии и операций переброски , каждая из которых состоит в преобразовании выбранного перекрёстка, содержащегося в некотором шаре, в противоположный перекрёсток (верхнее ребро становится нижним и наоборот, рис. 1, также см. [2]). При изотопии коэффициент зацепления не меняется, следовательно достаточно проверить, что при переброске, применённой к некоторой паре рё-

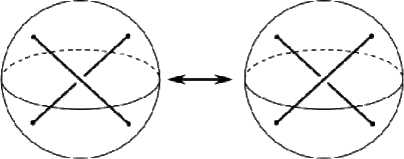
Рис. 1. Операция переброски

бер a , b е E ( G n , _m ), значение функции m 2 не изменится.

Заметим, что при такой переброске для всех пар ( а , в ) е L _a , ь ( G n , _m ) коэффициент зацепления ik₂( а , в" ) меняется на единицу. Для всех остальных гамильтоновых пар циклов из множества Г ( G n , _m ) \ L _a , ь ( G n , _m ) коэффициент зацепления не меняется. В силу теоремы 1 множество

L _a , b ( G n , _m ) чётно. Следовательно, при переброске значение функции m 2 не меняется. Следствие 1

доказано.

2.    Тривиальность функции ю2

Пусть { e 1 , - , e _l } с E ( K n ) - набор рёбер в полном пространственном графе K n с n >  6 вершинами. Как и раньше, будем обозначать Г ( K n ) множество всех гамильтоновых пар циклов в графе K n . Обозначим Г _е 1 _{e i} с Г ( K n ) множество гамильтоновых пар циклов, проходящих по всем выбранным рёбрам е 1 , — , e i . Также для произвольного подмножества L с Г ( K n ) определим значение функции s ₂ ( L ) как остаток от деления на 2 суммы

£ ^l k 2^{( а} , ^{в )} .

( а , в )е L

Отметим, что s ₂ ( Г ( K n ) ) = m ^ ( K n ).

Полный пространственный граф будем называть каноническим , если он получается следующим образом (такой граф рассматривался в [2, S], также см. рис. 2):

• 1.    Располагаем вершины v 1 , - , v n в вершинах правильного n -угольника, лежащего в плоскости Oxy пространства R ³;

• 2.    Опускаем каждую вершину v i , i = 1,..., n на i - 1 единиц вниз;

• 3.    Соединяем все вершины попарно между собой прямолинейными отрезками.

Лемма 1. Пусть е е E ( K n ) - ребро полного пространственного графа K n , n >  8. Тогда s ₂ ( Г _е ) = 0 .

Доказательство. Пусть редуцированный полный пространственный граф G n 1 получается из полного пространственного графа K _n удалением ребра e . Тогда

® 2 ⁽ G n ,1 ) = ® 2 ⁽ K n ) + ^s 2 ^{( Г} е ) , где сложение осуществляется по модулю 2.

Из теоремы 1 и [2, Теорема 1] следует, что значения ^ 2 ( G n 1 ) и to 2 (K n ) не зависят от пространственных вложений. Следовательно, для вычисления значения s ₂( Г _е ) можно считать, что пол-

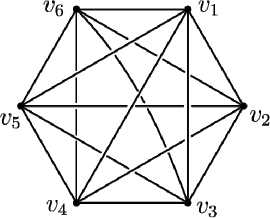
Рис. 2. Канонический полный пространственный граф с шестью вершинами

ный пространственный граф Kn является каноническим. Также будем считать, что ребро е ин- цидентно вершинам v1 и v2 .

Рассмотрим инволюцию т: Kn ^ Kn, индуцированную следующим отображением вершин графа Kn: все вершины v3,...,vn остаются неподвижными, а вершины v1 и v2 меняются места- ми.

Пусть ( а , в ) е Г _е . С точностью до переобозначений можно считать, что компонента а проходит по ребру е . Рассмотрим гамильтонову пару циклов ( а ¹, в ) е Г _е , где а ' = т ( а ). Если ( а ¹, в ) = ( а , в ), то компонента а является треугольником, причём образующие её рёбра (кроме ребра е ) проходят выше всех остальных рёбер графа K n . Тогда lk ₂ ( а , в ) = 0.

Если (а1,в) * (а,в), то из построения следует, что при инволюции т индексы двойных то чек, образованных рёбрами компонент а и в, сохраняются (рис. 3). Тогда lk2 (а,в) = lk2(а',в) •

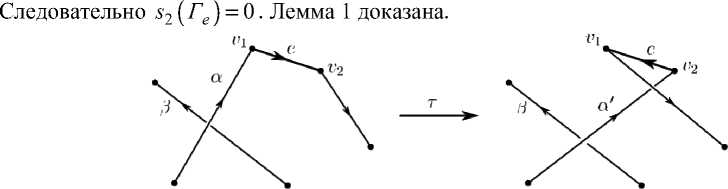
Рис. 3. При инволюции т индексы двойных точек, образованных рёбрами компонент а и в , сохраняются

Лемма 2. Пусть е 1 , е ₂ е E ( K n ) - два смежных ребра полного пространственного графа K n , n >  8. Тогда s 2 ( Г 1 , е 2 ) = 0.

Доказательство. Пусть редуцированный полный пространственный граф G _{n ,2} получается из полного пространственного графа K _n удалением смежных рёбер е ₁, е ₂ . Тогда

® 2 ( G n ,2 ) = ® 2 ^{( K}n ) ^{+ s} 2 ( ^Г е 1 ) ^{+ s} 2 ( ^Г е ₂ ) ^{+ s} 2 ( ^Г е 1 , е ₂ ) , где сложение осуществляется по модулю 2.

Из того, что значения ^ 2 ( G n ₂) и ffi ^ ( K n ) на зависят от пространственных вложений графов и из леммы 1 следует, что значение s ₂ ( Г _е 1 _е^ ) также не зависит от конкретного пространственного графа K n . Поэтому будем считать, что этот граф K n является каноническим. Также будем считать, что ребро е 1 инцидентно паре вершин ( v 1 , v ₂), а ребро е ₂ инцидентно паре вершин ( v ₂, v з ). Рассмотрим инволюцию т : K n ^ K n , которая индуцирована следующим отображением

Математика

вершин графа K n : все вершины v ₄, . , v n и вершина v ₂ остаются неподвижными, а вершины v ₁ и

• v ₃ меняются местами.

Пусть ( а , в ) е Г _е . Без ограничения общности можно считать, что компонента а последовательно проходит по рёбрам е₁ и е ₂. Рассмотрим пару (а',в), где а ' = т ( а ). Если ( а ¹, в ) = ( а , в ), то из построения следует, что компонента а является четырёхугольником, проходящим через вершины v 1 , v ₂, v ₃ и некоторую вершину v i . Тогда, так как рёбра графа K n , инцидентны парам вершин ( v 1 , v i ) и ( v ₃, v i ), проходят выше всех остальных рёбер, то lk ₂ ( а , в ) = 0.

Если ( а ¹, в ) * ( а ,в), то из построения следует, что lk ₂ ( а , в ) = lk ₂( а ', в ) (см. рис. 3). Следовательно $ ₂ ( Г^ _е 2 ) = 0. Лемма 2 доказана.

Теорема 2. Пусть G n m - редуцированный полный пространственный граф, n >  8, 0 < m < n - 2. Тогда m 2 ( G _nm ) = 0.

Доказательство. Пусть редуцированный полный пространственный граф Gn m получается из полного пространственного графа Kn удалением рёбер е1,е2,...,em е E(Kn), инцидентных одной вершине графа Kn . Тогда из принципа включения-исключения следует, что m

®2 (Gn,т ) = ®2 (Kn ) + ^$2 (Ге, ) +    £    $2 (Ге,1,е,2 ) + .+ i=1                {ii, i 2}g{1,., m }

• ⁺         ^        $ 2^{( Г е} ₄,..., ^е ,_{т - 1} ^{) +} $ 2⁽ ^i,...,^е т )»

{ ii,..., im-1}C{1,., m} где сложение осуществляется по модулю 2.

Заметим, что Г _е , , = 0 при к >  3. Следовательно, соотношение принимает вид

m

®2( Gn, m ) = ®2( Kn ) + £$ 2 ( Ге, )+     ^    $ 2 ( Ге,1, е,2 )• i=1                {ii, i 2}g{1,., m} m, и $2 (Ге е, ) = 0 для всех

Из лемм 1 и 2 следует, что $ ₂( Г _е ) = 0 для всех i = 1,

{ i ₁, i ₂} с {1,..., m }. Также из теоремы 2 работы [2] следует, что m ₂(K _n ) = 0 при n >  8 . Следовательно т 2 (G _n , _m ) = 0 . Теорема 2 доказана.

Можно показать, что существуют различные редуцированные полные пространственные графы, получающиеся из полного графа с шестью вершинами удалением одинакового числа рёбер, для которых значения функции m 2 также различны. Для этого рассмотрим канонический полный пространственный граф K ₆. Пусть V ( K ₆) = { v ₁,..., v 6 } (рис. 2). Этот граф содержит единственную пару циклов ( а , в ), для которой lk ₂ ( а , в ) = 1:

а = ( v 1 , v 3 , v 5 ) и в = ( v 2 , v 4 , v б ).

Тогда, если удалить из графа K ₆ ребро, инцидентное паре вершин ( v ₁, v ₂), то получится пространственный граф G ₆₁, для которого значение функции m 2 равно 1. Если же удалить ребро, инцидентное паре вершин ( v ₁, v ₃), то получится пространственный граф G '₆₁, для которого значение функции m 2 равно 0. Аналогичным образом строятся графы G _{6 2} и G _{6 3}, для которых значение функции m 2 равно 1. Эти графы получаются из K 6 удалением семейств рёбер {( v ₁, v ₂),( v ₁, v ₄)} и {( v ₁, v ₂),( v ₁, v ₄),( v ₁, v ₆)} соответственно. Графы G '₆₂ и G '₆₃, для которых значение функции m 2 равно 0, получаются из K ₆ удалением семейств рёбер {( v ₁, v ₃),( v ₁, v ₄)} и {( v ₁, v ₃), ( v ₁, v ₄), ( v ₁, v 5 )} соответственно.