Задача коррекции прикуса в зубочелюстной системе человека

Изменения зубочелюстной системы связаны с процессами питания, дыхания, глотания и речи, но они влияют и на весь организм человека. Зачастую не строятся взаимосвязи между патологическими процессами, происходящими в зубочелюстной системе и других системах организма человека, которые, на первый взгляд, не имеют ярко выраженных причинных связей [7–13]. Анализ изменений зубочелюстной системы предполагает персонифицированный подход ( patient specific ) в рамках концепции виртуального физиологического человека ( virtual physiological human ).

Основным из параметров, определяющих состояние зубочелюстной системы, является прикус (взаимное расположение верхней и нижней челюстей) (рис. 1). Предполагается проследить более подробно влияние изменений прикуса на состояние диска височнонижнечелюстного сустава и качественно оценить возможность биомеханического влияния изменений диска височно-нижнечелюстного сустава на мозговое кровоснабжение.

При коррекции прикуса зубочелюстной системы, связанной с потерей зубов, их повышенной стираемостью, травмами и переломами челюстей, стоматологи опираются на свой опыт и используют методики оценки взаимного положения верхней и нижней челюстей на основе геометрических расчетов, производимых в результате диагностики (рис. 2). Стоматолог, опираясь на диапазоны нормальных значений параметров, определенных в процессе диагностики [14], корректирует прикус, изменяя высоту и характер смыкания зубов верхней и нижней челюстей, применением различных ортопедических конструкций и ортодонтического лечения (см. рис. 1) [1, 14, 15, 18]. В ходе процедуры коррекции прикуса стоматолога устраивает случай попадания параметров, определяющих состояние прикуса, в диапазон нормальных значений [14]. Он выбирает ортопедическую конструкцию, руководствуясь своим опытом. Таким образом, при коррекции прикуса оцениваются только геометрические параметры его состояния, которые косвенно позволяют установить, какие усилия возникают в элементах зубочелюстной системы. При этом косвенно, на основании опыта стоматолога, оценивается, сможет ли применяемая ортопедическая конструкция нести нагрузку, которая возникает в ней у конкретного пациента.

Состояние прикуса определяет нагружение всей нижней челюсти и височнонижнечелюстного сустава, поэтому необходимо биомеханическое сопровождение такой коррекции. Для объективизации методики коррекции прикуса нужны количественные оценки состояния диска височно-нижнечелюстного сустава и костной ткани нижней челюсти. В качестве количественной оценки предлагается рассматривать величины усилий, возникающих в диске височно-нижнечелюстного сустава и в самой нижней челюсти. Для этого поставлена задача управления коррекцией прикуса, в которой при определяемых параметрах прикуса напряжения в диске сустава, мыщелке и теле нижней челюсти не должны превышать заданных пределов для интенсивности напряжений.

Большинство стоматологов не применяет каких-либо измерений и методов диагностики для оценки состояния зубочелюстной системы человека. В настоящее время зубочелюстная система рассматривается как специализированная, многоблочная, многофункциональная биомеханическая [11–13]. Применение современных

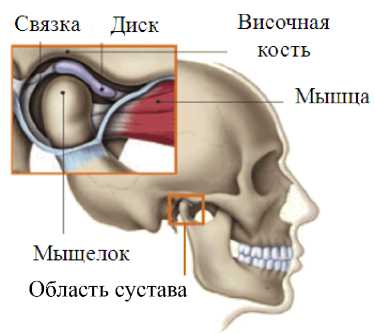
Рис. 1. Область височно-нижнечелюстного сустава

Сравнение с нормой

Работа с артикулятором

Временные конструкции

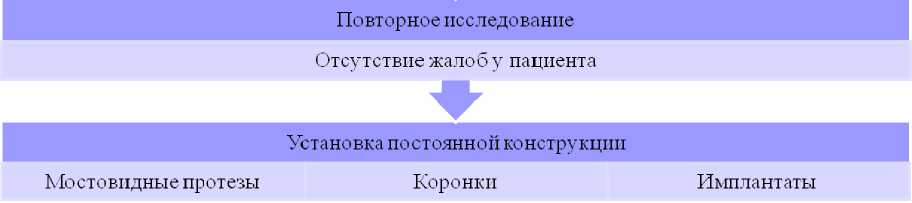
Рис. 2. Методика коррекции прикуса зубочелюстной системы [14]

методов диагностики состояния зубочелюстной системы не позволяет в полной мере оценить усилия, возникающие в ней. Ортопантомография (панорамный снимок), телерентгенография (фронтальный и боковой снимки), конус н о-лучевая и компьютерная томографии (трехмерная виз у ализация) позволяют оце н ить геометрические соотношения только костных элементов зубочелюстной сист е мы. Благодаря рентгеновским методам представляется возможным оце н ить геометрические размеры суставной щели височно-нижнечелюстного сустава между суставными поверхностями: суставным бугорком и ямкой височной кости и суставным мыщелком нижней челюсти.

Магнитно-резонансная томография применяется стоматологами реже по сравнению с вышеупомянутыми рентгеновскими методами по временным затратам. Она позволяет увидеть не только костные, но и мягкотканые структуры: мышцы, связки. А самое главное, магнитно-резонансная томография позволяет оценить положение диска височно-нижнечелюстного сустава относительно суставных поверхностей.

Для полного анализа состояния зубочелюстной системы недостаточно зн а ния только геометрии ее структур. Необходимо знать усилия, возникающие во в сей зубочелюстной системе, так как при превышении предельных значений появляются патологические изменения.

Для определения усилий в зубочелюстной системе необходимо поставить задачу определения напряженно-деформированного состояния нижней челюсти и диска височно-нижнечелюстного сустава под дей с твием усилий жевательных м ы шц, приводящих в движение нижнюю челюсть. На данный момент не существует метода, позволяющего количественно оценить усилия каждой мышцы in vivo [3, 16, 21, 24, 26].

П араметры зубочелюстной системы , анализируемые ПРИ РАСШИФРОВКЕ ТЕЛЕРЕНТГЕНОГРАММЫ

Телерентгенография – рентгеновский метод, основанный на получении фронтального и бокового снимков. Наибольший интерес представляет боковой снимок, благодаря которому можно оценить взаимоотношение верхней и нижней челюстей, положение и наклон зубов по отношению к челюстям, а также размеры суставной щели височно-нижнечелюстного сустава.

При анализе бокового снимка телерентгенограммы стоматолог отмечает ряд точек, отражающих геометрические аспекты зубочелюстной системы. При знакомстве с различными методиками расчета телерентгенограммы и подходами стоматологов (выделение на снимке тех или иных точек, определение линейных и угловых параметров) выяснилось, что каждый стоматолог выбирает удобный для себя метод и важные и необходимые для него параметры для коррекции прикуса.

При анализе телерентгенограмм основными показателями, характеризующими геометрию и состояние зубочелюстной системы, являются углы. В литературе описано, что линейные размеры челюстей и расстояния между специальными точками сильно варьируются, а угловые параметры имеют меньшие пределы, и для них в течение многолетних исследований установлена норма.

В ходе анализа телерентгенограмм были выделены три независимых параметра (угла), отвечающие за положение нижней челюсти относительно верхней (черепа):

• 1.    Угол ANB – угол, отвечающий за взаимное расположение челюстей (перекрывание челюстей) и характеризующий, на сколько нижняя челюсть позади или впереди верхней челюсти (в норме 2 ± 2º) (рис. 3).

• 2.    Угол FH–ML – угол, отвечающий за наклон нижней челюсти по отношению к верхней (черепу) (в норме 24 ± 3º) (рис. 4).

• 3.    Угол DoA – угол, отвечающий за наклон нижней челюсти по отношению к верхней (черепу) (в норме 43 ± 2 º) (рис. 5). На рис. 6 показан способ определения положения точки Xi .

Проанализируем, как координаты точек влияют на изменение вышеуказанных углов.

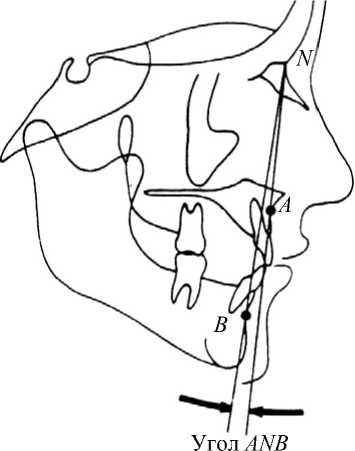
Рис. 3. Угол ANB , отвечающий за переднезаднее положение нижней челюсти относительно верхней (черепа)

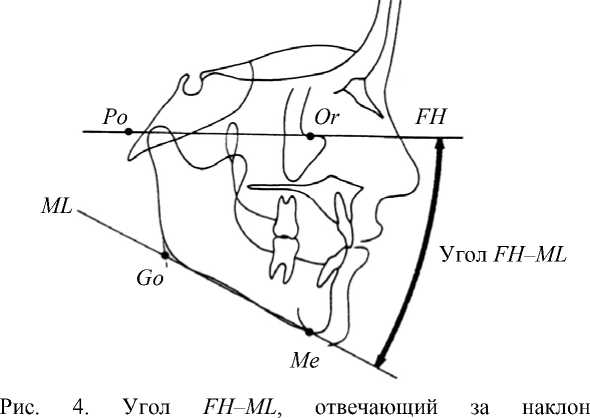
нижней челюсти относительно верхней (черепа)

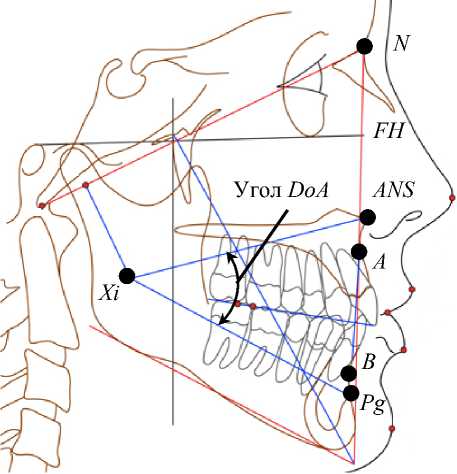
Рис. 5. Угол DoA , отвечающий за высоту нижней трети лица

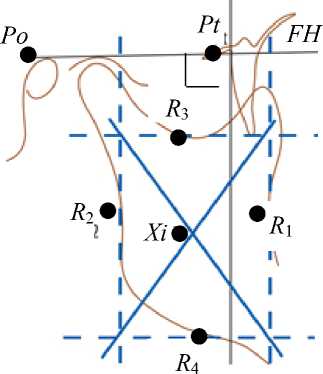
Рис. 6. Определение положения точки Xi

За изменение угла ANB отвечают координаты точек A , N , B . Точки A и N принадлежат верхней челюсти и черепу, соответственно, они жестко связаны. Расстояние между точками A и N является фиксированным, и его можно изменить только хирургическим путем. Точка B принадлежит нижней челюсти, и расстояние между ней и точками A и N может варьироваться. Соответственно, изменением только координат точки B можно повлиять на изменение угла ANB при коррекции нехирургическим путем.

За изменение угла FH–ML отвечают координаты точек Or , Po , Me , Go . Расстояния между двумя точками Me и Go , принадлежащими нижней челюсти и являющимися основой для прямой ML , и двумя точками Or и Po , принадлежащими черепу и являющимися основой для франкфуртской горизонтали (прямой FH ), являются постоянными.

Изменение угла DoA определяется изменением координат точек Xi и Pg относительно точки ANS верхней челюсти (положение которой жестко связано с точками A , N и другими точками верхней челюсти), при условии, что расстояние между точками Xi и Pg является фиксированным (принадлежат нижней челюсти) (см. рис. 5).

Выбор переменных, определяющих положение прикуса

Движение твердого тела в общем случае описывается системой из шести уравнений. Таким образом, при первоначальной постановке прикуса есть шесть независимых переменных, управляя ими можно привести нижнюю челюсть в нужное положение. В ходе коррекции прикуса стоматолог приводит стоматологические параметры в норму, которая является не набором конкретных значений параметров, а диапазонами их изменения.

Биомеханическое моделирование позволяет выбрать вектор значений, т.е. из диапазона каждого из параметров выбрать конкретное значение. При выборе конкретных значений необходимо учитывать усилия в мышцах, напряжения и деформации, возникающие в мыщелке нижней челюсти и диске височнонижнечелюстного сустава.

Рассмотрим случай центральной окклюзии при выборе прикуса стоматологом для симметричного случая (нижняя челюсть имеет плоскость симметрии xOz ). Будем рассматривать коррекцию прикуса в сагиттальной плоскости. При этом движение нижней челюсти можно считать плоскопараллельным, при нем положение нижней челюсти будет определяться системой из трех уравнений, включающих изменение координат точки А (полюс) и изменение угла поворота φ вокруг полюса:

' Уа = у ⁽ t ) ,

^ - = ^ ( t ) , ⁽¹⁾ _ ф = ф ( t ) .

Через параметры системы (1) можно выразить стоматологические параметры, определяемые при помощи телерентгенографии. Стоматолог на получившемся боковом снимке телерентгенограммы отмечает реперные точки (например, точка A ) и производит вычисления и анализ параметров (например, угол ANB ) (см. рис. 3). Далее, на основании полученных значений параметров выбирается план ортопедического лечения, который заключается в выборе конкретных значений параметров, входящих в диапазоны физиологических значений, и методов достижения этих выбранных величин (применение тех или иных ортопедических конструкций).

Стоматологи стремятся изменить не только параметры таким образом, чтобы они входили в диапазоны нормальных значений, но и их значения, чтобы они были как можно ближе к средним значениям.

Из анализа вышеупомянутых параметров и литературного обзора методик рассмотрения состояния зубочелюстной системы следует, что в этих работах напрямую не затрагивается состояние и положение диска височно-нижнечелюстного сустава. Наверное, это связано с тем, что рентгеновские методы практически не способны визуализировать мягкотканые и хрящевые структуры. Соответственно, они не могут даже качественно дать информацию о состоянии и патологических процессах в диске височно-нижнечелюстного сустава.

Опосредованно о положении диска височно-нижнечелюстного сустава можно судить по анализу состояния суставной щели височно-нижнечелюстного сустава между суставными поверхностями мыщелка нижней челюсти и суставной ямки и бугорка височной кости. В литературе описаны размеры суставной щели в норме. Компьютерная томография (как наиболее современный рентгеновский метод) позволяет четко увидеть размеры суставной щели, но не позволяет оценить состояние и положение диска в отличие от магнитно-резонансной томографии.

На боковом снимке магнитно-резонансной томографии можно оценить положение и состояние диска височно-нижнечелюстного сустава, а также выделить точку приложения реакции в суставе [2, 17, 19, 20, 25]. Она находится путем определения кратчайшего расстояния между суставными поверхностями при условии, что принадлежит поверхности мыщелка и диску височно-нижнечелюстного сустава. В этой точке будут прикладываться реакции при определении усилий мышц в процессе смыкания челюстей (рис. 7).

Рассматривая нижнюю челюсть в первом приближении как абсолютно твердое тело, можно сказать, что углы ANB , FH–ML и DoA описывают положение нижней челюсти относительно верхней (черепа), а также положение точки приложения реакции.

Таким образом, за положение нижней челюсти, а также точки приложения реакции по отношению к верхней (черепу) можно выбрать координаты точки B (или Pg ) и угол поворота вокруг точки B (или Pg ), т.е. три параметра (координаты полюса и угол поворота вокруг полюса, описывающие плоскопараллельное движение нижней челюсти).

Анализ стоматологических параметров, которые были упомянуты выше, позволил понять, что для однозначного описания положения нижней челюсти при плоскопараллельном движении достаточно этих трех параметров.

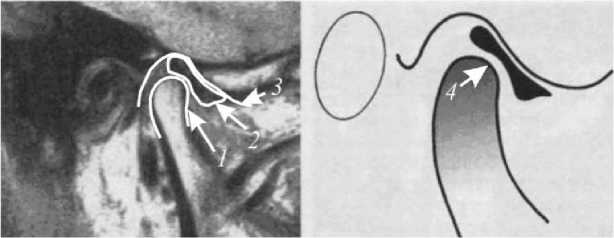
Рис. 7. Магнитно-резонансная томография височно-нижнечелюстного сустава в кососагиттальной проекции (проекция, выполняемая под углом к сагиттальной): 1 – мыщелок; 2 – диск; 3 – суставная ямка и бугорок; 4 – центральная зона диска и вектор жевательной нагрузки, которая противоположна и равна по величине реакции в височно-нижнечелюстном суставе. Нормальное взаиморасположение суставных структур при центральной окклюзии [14]

Постановка задачи биомеханического сопровождения коррекции прикуса

В практике стоматолог в процессе анализа состояния зубочелюстной системы с использованием расчетов на телерентгенограмме отмечает большое количество точек и анализирует множество параметров. Не все выделяемые стоматологом параметры являются независимыми. Многие из них зависят от других и путем применения математических операций выводятся друг из друга.

В данной работе авторы выделили те независимые параметры, которые оказывают влияние и на геометрию, и на напряженно-деформированное состояние зубочелюстной системы.

В качестве параметров, определяющих положение нижней челюсти, были выбраны углы ANB , DoA и FH-ML , т.е. U = { Z ANB , Z DoA , Z FH-ML } . Для каждого из них существуют диапазоны нормальных физиологических диапазонов: 0 ANB < 4 ° ,41 ° DoA < 45 ° ,15 ° FH-ML <  25 ° , со средними (физиологическими) значениями: Z ANi = 2 ° 2 ° , Z DoA_aver = = 43 ° , Z FH - ML_aver = 2= 20 ° . average                  average                          average

Координаты точки B (или Pg ) и угол поворота вокруг этой точки задают положение нижней челюсти относительно верхней (черепа). При изменении координат этой точки и повороте изменяются координаты точек крепления жевательных мышц к нижней челюсти и углы наклонов этих мышц по отношению к франкфуртской горизонтали.

Прикус, определенный стоматологом, задает положение статического равновесия нижней челюсти по отношению к верхней. Это положение челюсти определяется набором параметров U = { u 1 ,u ₂,..., u m }. Физиологическая норма прикуса - диапазоны значений ni < u i <  й i , т.е. физиологическая норма представляется m -мерным параллелепипедом П _m . При центральной окклюзии m = 3, а при отсутствии симметрии m = 6.

Задача коррекции прикуса состоит в следующем. Когда стоматолог назначает положение прикуса, тогда, согласно изложенному выше, определены конкретные значения U еП _m , принадлежащие диапазону физиологической нормы для данного пациента. Обычно повторные обращения пациента к врачу связаны с коррекцией прикуса в этом диапазоне. Поставим задачу коррекции прикуса методами биомеханики.

Будем варьировать значения U еП _m в физиологическом диапазоне. Каждый набор таких параметров с помощью решения статически неопределенной задачи вычисления усилий мышц и реакций височно-нижнечелюстных суставов позволяет найти значение целевой функции, равное M ^* , отражающей напряженность жевательных мышц, M * е M = [0,1] . Задача построения целевой функции рассмотрена ниже. Для каждого набора U имеется точка M ^* , принадлежащая множеству M . Тогда будем искать такой набор параметров прикуса U ^* , при котором достигается минимум значений целевой функции Ф = min M * .

U еП m

Таким образом, задача биомеханического управления коррекцией прикуса выглядит следующим образом.

Найти

Ф = min M * ,                               (2)

U еП m при ограничениях

^C i res ,                                         (3)

^C i <^C col .                                         ⁽⁴⁾

Здесь C i - интенсивность касательных напряжений; C _res - максимальная интенсивность напряжений, при которых не наблюдается резорбция костной ткани в мыщелке нижней челюсти; C co - максимальная допустимая интенсивность напряжений в диске височно-нижнечелюстного сустава. Для выполнения ограничений (3)–(4) требуется при построении множества M решение задач теории упругости для определения напряженно-деформированного состояния диска височнонижнечелюстного сустава и нижней челюсти. При различных значениях U еП m будут получены различные усилия мышц и реакции сустава. Критерий (2) устроен таким образом, что позволяет избежать перенапряжения мышц зубочелюстной системы, доступных и не доступных при пальпации стоматологом, что может приводить к болевым ощущениям, перегрузке диска, неправильному процессу открывания и закрывания рта.

При заданном положении прикуса определим величины усилий мышц и реакцию в височно-нижнечелюстном суставе с помощью раскрытия статической неопределенности при использовании критерия оптимизации. Его выбор обсуждается в работах [3, 9, 22, 24].

При заданном положении прикуса имеет место статическое равновесие нижней челюсти. Условия статического равновесия можно записать в виде уравнений (5) и (6):

N 2

2 F i + 2 R + F b = 0 ,                      (5)

i = 1            j = 1

N 2

наименьшего предела текучести для стержней вся несущая способность осуществляется вторым стержнем, имеющим больший предел текучести.

Определим вектор значений мышечных сил X = { F 1 , F 2,... , F N } и функции

F fl (X) = L’ гДе i е[1,2,-’N] и F,max i ,max

– максимальная мышечная сила i -й мышцы,

которая определяется как

F _m = к KA,. . i , max          i

Здесь K – удельная мышечная сила, определенная экспериментально для того типа мышц, к которому относятся мышцы зубочелюстной системы, K к 37 Н - см^-2 [15]; A i - физиологическое поперечное сечение i -й мышцы.

Определим множество Q, образованное теми значениями X , при которых выполняются уравнения равновесия (5) и (6). Тогда требуется найти точку X * eQ (значения усилий мышц), для которой

max f ( X * ) = min max f ( X ) . i e [1,2, _ , N ] i ^{x 7} X Q i e [1,2, _ , N ] ' ^{X 7}

Таким образом, точка X * , определенная критерием (8), разыскивается как

минимум

наиболее системы.

Из

F среди максимальных значений отношений i , что обеспечивает

F i ,max равномерное вовлечение в действие всей группы мышц зубочелюстной

вида целевой функции следует, что необходимо осуществлять поиск

минимума среди континуума максимальных значений (задача на минимакс). Целевая функция для данной задачи является дискретной функцией номеров мышц. Но данная дискретная функция может быть преобразована в линейную целевую функцию (9) с N дополнительными линейными ограничениями (10) и (11).

Введем функцию ц ( X ) = i max N f ( X ) . Очевидно, значение максимума принадлежит ограниченной области 0 <  ц < 1 . Тогда будем решать следующую задачу.

Найти такой вектор усилий X * , при котором достигается min ц ( X ) XeQ   ^{Х 7}

при ограничениях

f ( X ) < Ц, 0 <  ц <  1 ,

где i е [1,2, _ , N ] .

Для каждого найденного вектора усилий X * значение целевой функции (9) определяет величину M * , т.е. M * = min ц ( X ) . При изменении управляющих параметров U строится множество M , что и позволяет в дальнейшем найти Ф = min M * и тем самым решить задачу управления (2)-(4).

U еП m

Таким образом, от первоначальной дискретной задачи оптимизации с шестью ограничениями осуществляется переход к линейной задаче оптимизации с целевой функцией (9), в которой целевая функция ц ( X ) должна быть минимизирована, удовлетворяя условиям N + 6 линейных ограничений уравнений (5), (6) и (10), (11) с двумя дополнительными условиями.

• 1.    Мышечная сила должна быть больше нуля или равняться нулю. Данное ограничение обусловлено следующим обстоятельством: с точки зрения механики сухожильно-мышечные комплексы следует рассматривать как односторонние связи, так как они способны сопротивляться растяжению и, подобно гибким нитям, выключаются из работы при появлении в них сил осевого сжатия.

• 2.    Можно использовать экспериментальные данные о том, что суставные реакции по оси x должны действовать в заднем направлении; суставные реакции по оси z должны действовать в нижнем направлении [14, 23, 24]. Данное ограничение может быть использовано, потому что при сжатии наибольшее число мышц действует вперед и вверх, таким образом суставная реакция должна противодействовать мышечным силам, чтобы поддерживать статическое равновесие. Это ограничение не является обязательным.

Целевая функция (9) ограничена сверху, а ограничения (5), (6) и (10) линейны. Так как переменные задачи заданы на пересечении замкнутого отрезка (ограничение для величины ц ), плоскости (для реакций) и полуплоскости (для величины усилий в мышцах) (выпуклые множества), то ввиду линейности ограничений, а значит их непрерывности, область, заданная ограничениями, является выпуклой и замкнутой. Такая задача является классической задачей линейного программирования и имеет единственное решение, поэтому она может быть решена симплекс-методом для линейного программирования.

Окончательно решаемая задача может быть сформулирована следующим образом: найти

min u. ( X ) XeQ ^V '

при ограничениях

N 2

• У    Fix + У Ri,+ Fbx = 0, ixjxbx i=1

N 2

Z F i y ■ Z R j , + F b y = 0.

i=1

N 2

• У    Fz + У Ry + Fb = 0, izjzbz, i=1

  
  

N 2

Ум +y м, +m, =o ixjxbx i=1

N 2

Z Miy + Z M,y + Mby = 0 i=1

N 2

• У    Mi_z + У m i + M_h = о i z

i=1

0 < u < 1 ,

F i ^ 0,

F i

< ц ,

F i, max где Fi – усилие, развиваемое i-й мышцей (i = 1, …, N); Rj – реакция височнонижнечелюстного сустава (j = 1, 2); Fb – сила сжатия челюстей; Fi ,max – максимальное усилие, развиваемое i-й мышцей.

В результате решения находятся мышечные усилия и реакции в суставах.

В итоге решаются две связанные задачи: определение усилий мышц и реакций в височно-нижнечелюстных суставах в процессе смыкания челюстей (приложена сила сжатия) и определение напряженно-деформированного состояния нижней челюсти и диска височно-нижнечелюстного сустава при двух фиксированных значениях параметров и при изменении третьего (например, величины углов DoA и FH–ML фиксируются и меняется величина угла ANB в диапазоне нормальных значений). Далее фиксируются величины углов ANB и DoA и меняется величина угла FH–ML . В последнем случае фиксируются величины углов ANB и FH–ML и меняется величина угла DoA . Набор этих углов составляет вектор управляющих параметров U = { u 1 , u 2 , u 3 } , по которым ищется минимум целевой функции (задачи (2)–(4)).

В каждом случае для каждого значения варьируемого параметра определяется точка приложения реакции височно-нижнечелюстного сустава, находятся усилия мышц и реакция височно-нижнечелюстного сустава, вычисляются напряжения в нижней челюсти и диске височно-нижнечелюстного сустава, а также сравниваются с предельными значениями. Важно   также,   что определяется значение

F ц (X) = max ft (X) , где X = { F1, F^,_, F^}, функция f (X) = —---, i e[1,2,..., N ] и е[1,2,^, N ]

i ,max

F – максимальная мышечная сила i -й мышцы. i ,max

При решении всех задач для вышеупомянутых случаев фиксируемых и варьируемых параметров определяется множество значений µ, т.е. ц = ц ( Z ANB , Z DoA, Z FH-ML ) . Каждой точке с координатами ( Z ANB , Z DoA, Z FH-ML ) соответствует некоторое значение ц, являющееся элементом множества M (11). Нас интересует минимальное значение µ при условии, что напряжения при этом ц = M * не превышают заданных пределов (задача (2)-(4)).

Окончательно решение последовательности поставленных задач составляет методику биомеханической коррекции прикуса, результатом применения которой является объективизированный набор параметров, определяющих прикус. Это позволяет ввести в практику стоматологии количественные соотношения, что должно привести к уменьшению числа повторных посещений стоматолога. На рис. 8 представлена схема применения методики [6].

Таким образом, поставленная задача управления коррекцией прикуса заключается в следующем. У заданного стоматологом положения прикуса имеется физиологический диапазон, в котором меняются управляющие параметры U. Для каждого такого набора решается задача определения усилий мышц и реакций в суставах (задача (12), (13)). Для каждого решения имеются различные значения целевой функции (12), которые позволяют построить множество M и решить задачу (управления (2)–(4)).

Визуальный осмотр

Граница улыбки

Па льпация Анамнез ( жалобы, мышц       заболевания)

Рентгеновский метод исследования

.омпьютерная томография

Уртопантомо-   Телерентгенография          гравия

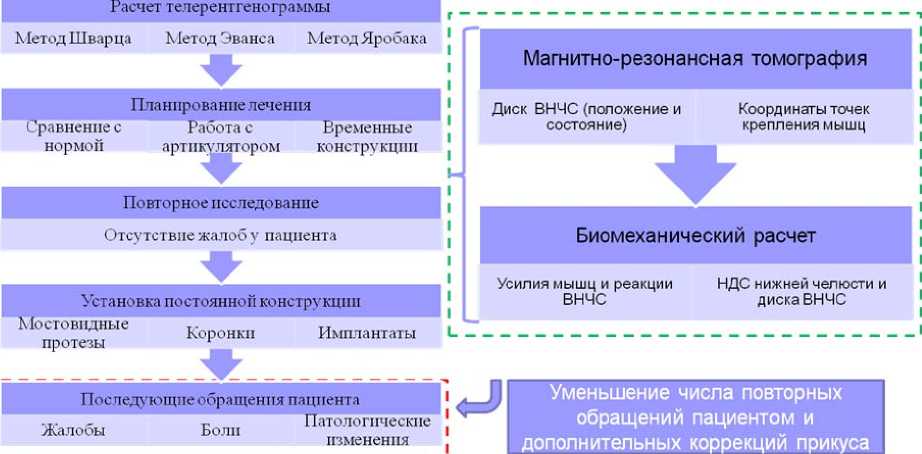
Рис. 8. Методика биомеханического сопровождения коррекции прикуса: ВНЧС – височно-нижнечелюстной сустав, НДС – напряженно-деформированное состояние

Заключение

Возможно, стоматолог выскажет мнение, что на практике сложно достичь значений углов ANB , DoA и FH–ML , которые рекомендуются авторами для данного пациента, тогда он сможет рассмотреть те случаи, в которых значения близки к рекомендуемому на основании биомеханического моделирования. Реализовать их можно, применив те или иные ортопедические конструкции.

Полученные результаты позволяют дать объективные количественные оценки усилий, возникающих в нижней челюсти и диске височно-нижнечелюстного сустава для конкретного пациента, и дать долговременный прогноз возникновения патологических процессов, связанных с коррекцией прикуса.

Благодарности

Работа выполнена при финансовой поддержке РФФИ (грант № 15–01–04884–а, «Биомеханическое моделирование формирования и развития трабекулярной костной ткани в различных отделах скелета человека в норме и при патологии»).