Задача Коши для уравнения изгибных колебаний нелинейно-упругого стержня бесконечной длины

В области (x, t) € R¹ х R +, R¹ =] - то, +то[, R + =]0, +то[, рассмотрим уравнение, описывающее изгибиые волны в нелинейно-упругом стержне¹ (см. [1, с. 55], [2, с. 189], обзор и подробную библиографию, приведенные в монографии [2]):

du — dSc + a' £ = в£ ^

где заданные числа a € R+, в € R¹.

Полагаем, что д ^ - начальные функции задачи Коши:

^u| t=0 = Д^(х), u t|t=o = W^{x )}, ^{x € r1},                         (2)

и искомое классическое решение² u = u(x, t), (x, t) € R¹ XR +, R + = [0, +то [, уравнения (1) для всех значений временной переменной t по переменной x принадлежат банахову про

странству C [-то, +то] = C [R¹] ³ непрерывньix функций g = д(х), для которых существуют пределы при х ^ ±то, и норма определяется по формуле kg(x)kc = sup_xGRi |д(х) |.

Будем обозначать C ^[R¹ ] = ^{д(х) G C [R¹] : g' (x),... ,g^(k)(x) G C [R¹]}.

Наша цель — для случая в = 0, т. е. для соответствующего (1) линейного уравнения, найти явный вид решения задачи Коши в пространстве C [R¹], а в случае в = 0 - найти временной отрезок существования классического решения задачи Коши и оценить норму в C [R¹] этого локального решения, далее рассмотреть условия существования глобального (определенного для t G R^) решения уравнения (1) и разрушения его решения на конечном временном отрезке.

• 2.    Задача Коши для линейного уравнения изгибных волн

Рассмотрим линейное однородное уравнение, соответствующее (1):

d²u    д ⁴и      ₂ д⁴ и

+ а²

dt2   дx2дt2     дх4

Наличие при А > 0 резольвенты днффореипиалыюго оператора, d2/dx2 позволяет существенно преобразовать уравнение (3), разрешив его относительно производной по времени. Именно, пусть и = u(x,t) — классическое решение задачи Коши (1), (2), для которого частные производные uxx, uxxt непрерывны при t > 0. Введем новую неизвестную функцию v = и - Uxx. (4)

Из замены (4) можно единственным образом определить начальные значения v|t=₀ = ^(х) - ^' (х), v_t |t=₀ = ^(х) - ^''(х) при условии, что функции ^(х), ^(х) принадлежат C ⁽²⁾ [R¹] и выразить [3, с. 682] решение u(x,t) задачи Коши (1), (2) через новую неизвестную функцию v(x,t):

и(х, t) = I -

d2 А dx2 )

v

+ ^

(^t)=I /

e

^|r|v(x + r, t) dr.

-∞

В результате подстановки (4) уравнение (3) в пространстве C [R¹] можно записать в виде абстрактного обыкновенного дифференциального уравнения

V tt = GoV, t G R+, ( 6 )

где V = V(t) : t R v(x,t) - искомая вектор-функция, определенная для t G R+, со значениями в пространстве C [R¹]. Операторный коэффициент в уравнении (6) - линейный оператор G_o = -а² (I - d²/dx²)^-1d⁴/dx⁴ - определен на, функциях д(х) G C ⁽⁴⁾[R1] и его можно продолжить до оператора G = A + o?I + B, где A = a²d²/dx², B = -а²(I - d²/dx²) 1.

Таким образом, получим эквивалентное (3) интегро-дифференциальное уравнение utt = a2(uxx + u — h * u),                              h)

в котором h = e^-|x|/2 ii через h * ш обозначен а свертка: (h * ш)(—) = f+^ h(— — d)ш(d)dd Оператор A, D (A) = D (d² /d—² ), в C [R¹] [5, c. 92] является производящим оператором косинус оператор-функщш C (t; A). t E R¹. клащса C_o. для которс>й при всех g(—) E C [R¹] справедливо представление

C(t; A)g(—) = ^ и(at; — j + U\. — at; —

g(x) = 2 [g(— + at) + g(— — at)]

ii опенка нормы ||C (t; A) k 6 1. t E R¹.

Возмущенный оператор A + a²I. D (A + a² 1 ) = D (d²/d—²). также по рождает в C [R¹] [5. c. 1G9] косинус оператор-функцию C(t; A + a² 1 ). t E R¹. класса C_o. для которой справедливо представление

C (t; A + a² 1 )g(—) = C(t; A)g(—) + at

t j I1^apt2-s2) C (s; A)g(—) ^d— s2 , o

+ ^ ( z/ 2) 2^{k +1}

где g(—) — произвольныи элемент из C [R¹], a 11(z) = k =o= o k !( k +1)! модифицированная функция Бесселя [6, с. 729], и оценка нормы |C (t; A + a²I)|| 6 ch(at), t E R¹.

Ограниченный оператор B. D(B ) = C [R¹]. порождает косинус оператор-функцию

C (t; B). t E R¹. класса C_o. которая для npoirзволыюго элемента g(—) Е C [R¹] представ

ляется [5, с. 142] степенным рядом, равномерно сходящимся по t на каждом конечном отрезке из R1:

C (t; B)g(—)

+ ^

= X n=0

(—1)n(at)2n (2n)!

I

-

d2 \ d—2

- n

g(—).

Откуда, применяя оценку нормы резольвенты (I — d²/d—²)^-1, выводим |C(t; B )| 6 ch(at), t E R¹. Используя формулу [3, с. 664], выражающую степени резольвенты (I — d²/d—²)^-n через полугруппу, порождаемую оператором d²/d—²:

I

-

d2 \ d—2

- n

g^(—) = щ-( n

1)!

+ ^

/ sn-1 o

2 e-sU( s;

d—2

g() ds,

преобразуем представление косинус оператор-функции C (t; B ):

C (t; B )g(—)= g(—) — (^t^ [ e^-s o F 2 (;³, 2; — (^s )ufs; -d²,) g(—) ds,    (10)

2                 2       4            d— /

o где 0F2 (; 3/2, 2; —z/4) = 2 P+=°o П-^^, - обобщенная гипергеометрическая функция [7, с. 437]. Далее, применяя интегральное представление полугруппы U(s; d2/d—2), формуле (10) можно придать вид

C (t; B )g(—) = g(—) —

2 ⁺“

(at)- j F ((at)²,e²) g(— + ^) d^,

-∞

t E R¹,

(И)

где обозначено F (z,^²)= J^^ e ^s ^2^/(4s)_oF₂ (; 3/2, 2; —z/4s)ds/Vs-

Возмущение ограниченным оператором B сохраняет способность оператора A + a21 порождать косинус оператор-функцию класса C0 [5, с. 169], поэтому оператор G является производящим оператором сильно непрерывной косинус оператор-функции класса C0, для которой на, элементах g(x) G D(G) = D(d2/dx2) справедливо представление t2

C (t; G)g(x) = C (t; A + а² 1 )g(x) + —

У 31 (tp1 - Z ², A + a²I )c (tz ; B)g(x) dz, 0

t G R¹,

где 31 (t, A + a² 1)g(x) = 4/n /1 p1 — n² C(tn; A + a² 1)g(x) dn-

Используя формулы (8), (9), (И), косинус оператор-функция, порождаемая оператором G. записывается в явном виде на. функциях g(x) G D (d²/dx²):

C(t; G)g(x) = 2 [g(x + at) + g(x

t

+ аГ /11 (aPt² — s2) [g(x + as) + g(x ' о

— at)]

^^^^^^^^r

ds as) .          :

Pt^—s2

21       1

+tn У dZ У P1 — n² g (x + atnp1 — Z ²) + g (x

^^^^^^^^r

atnpl — Z ²)

^^^^^^^^r

(4^ У F (^(atZ)2, ^€2) g (x ⁺ € ^{+ a}tnp1 ^{— z2})

-∞

+ g x + € —

atnp 1 — Z ² ) d€ + atnp 1 — Z ²

У   I1 (apt²n² (1 — Z ²) — s²)

о

x g(x + as) + g(x — as)

r

+∞

^ /f (^)2,€2⁾

4 yn

x [g(x + € + as) + g(x + € —

-∞ as)] d€ —,        s----

^J J Pt²n²(1 — Z ²)

r

s 2 ^dη

и для нее справедлива оценка, нормы

||C (t; G)| 6 ch(at) + a ²sh (at(p2 — 1))sh (at(p2 + 1)), t G R¹.

С косинус оператор-функцией (12) ассоциируют [5, с. 91] синус оператор-функцию:

t

S (t; G)g(x) = j о

C (r; G)g(x) dr,

g(x) g C [R¹],

и линейное многообразие C1[R1] = {g(x) G C [R¹] : C (t; G)g(x) G C ⁽¹⁾(R1; C [R¹])}, t. e. подмножество C1[R1] пространства C [R¹] состоит из тех элементов пз C [R¹]. для которых функция C (t; G)g(x) : R¹ ^ C [R¹] является непрерывно дифференцируемой функцией переменной t.

Очевидно, что D (G) = D (d²/dx²) С C1 [R¹].

Используя оценку (13), имеем

t l№ G)k 6 j kC(s; G)k ds

6 |s^h(at) | + α

sh(2atV2)    sh(2at)

-

4a3 V2       4a3

, t E R¹.     (15)

Таким образом, приходим к абстрактному дифференциальному уравнению, обобщающему уравнение (6) в банаховом пространстве C [R¹]:

V tt = GV, t E R+,

в котором операторный коэффициент G порождает сильно непрерывную косинус опера-тор-фмиктшю класса C0. Начальные' условия в C [R¹] для уравнения (16) перепишутся в виде

V U = Ф, V lt=o = Ф, (17)

где Ф = ^(x) - ^' (x). Ф = ^(x) - ^"(x) - элементы пространства, C [R¹].

Для того чтобы задача Коши (16), (17) была равномерно корректной⁴ на R+, необходимо и достаточно, чтобы оператор G был производящим оператором сильно непрерывной косинус оператор-функции класса C0, при этом классическое⁵ решение задачи Коши (16), (17) дается [5, с. 91-92] формулой V(t) = C (t; G)Ф + S (t; G) Ф, t E R¹, для любых Ф E D (G) 1i Ф E C1 [R¹].

Теперь, производя обратную замену (5) и используя перестановочность резольвенты (I - d2/dx2)-1 с косинус оператор-фупктщей. порождаемой оператором G. находим решение задачи Коши для уравнения (3):

u =

2 -1

(I -        V(t) = C (t; G) у + S(t; G) ^.

dx2

Таким образом, имеет место утверждение6:

Теорема 1. Пусть начальные функции y(x), ^(x) вместе с производными до четвертого порядка включительно принадлежат пространству C [R¹]. Тогда задача Коши для линейного однородного уравнения (3) равномерно корректна, классическое решение

4 Задача. Коши

u⁰ (t) = Au(t), t E R+; u(0) = u⁰, u (0) = u¹,

(*)

в банаховом пространстве E называется равномерно корректной [5, с. 89], если найдется плотное подмножество Ei С E такое, что при u⁰. u¹ E Ei существует сдинственное решение на. R. и это решение равномерно устойчиво по t на. любом компакте K С R. т. е. из условия um — 0 К E Ei. m = 0,1) при n - у следует сходимость соотвстствугощих решение! u„(t) — 0 равномерно по t E K. где 4™° (0) = um. m = 0,1.

• ⁵    Дважды непрерывно диффсрсицирусмая функция u(t) : R^ - E. т. е. u(t) E C ⁽²⁾ (Ry; E) называется классическим решением абстрактной задачи Коши (*), если u(t) E D (A), Au(t) E C (Ry; E) при t E R+ и удовлетвориютея равенства (*).

• ⁶    От пачальпой функции ^(x) требуем заведомо большую гладкость, чем нужно для существования решения задачи Коши для уравнения (3), чтобы не заниматься описанием подмножества Ci[R¹] пространства C [R¹ ].

дается формулой (18) или в подробной записи

t

1                                  1

u(x, t) = = [v(x + at) + v(x — at)] + =   [^(x + ar) + ^(x — ar)] dr

t

⁺ у j I i (^apt^{2 —} s²) ^[V^{(x + as) +} V^{(x — as)] p} t ₂ d — s ₂

tr ds pr2 — s2

⁺ 2 / rdr / 11 ,. ,     s) _Wx ^{+ as) +} ^x - ^as)]

t2

+

π

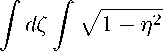
| V (x + atnpl — Z ²) + V (x

— atn pl — Z² }

—

₂ + ∞

^{( a}р Л j F (^(at^Z)2,p) [v (x ^{+ € + a}tnV1 ^{— Z2}) ⁺ V (^{x + €}

-∞

— atn pl — Z²} ] d€

⁺ t^v^ у I¹ ( ^p _W — ^z 2 ) — s²) |^v(x+as)+V(x —^as) 0

—

₂ + ∞

(^ j F (^(atZ)2,P) ^[v(x ^{+ € + as)+ V(}x ^{+ € — as)]} d^€    , _t 2 _n 2_{( 1}^ds _z 2 )

-∞

—

s2 dη

^^^^^^^^^

+1/ 0

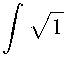
x

- arn 1 - Z2

(arZ ) 2 4РП

j F ((arZ) 2 , € 2 ) [^(x + € + arnpl — Z ²) + ^(x + € —

arn V 1 — Z ²   d€

-∞

rη 1 -ζ²

+ arqp 1 — Z ² У    I1 (ap r²n² (1 — Z ²) — s²)

x ^(x + as) + ^(x — as) —

+ ∞

(> /F ((«rZ) 2 .€ 2)

-

x [^(x + € + as) + ^(x + € — as)] d€

∞ ds

p r²n²(1 — z ²)

^^^^^^^^^

s2 dη dr

и для него справедлива, оценка sup |u(x,t)| 6 ch(at) + a-2sh(at(p2 — 1))sh(at(p2 + 1)) sup |v(x)| x∈R1                                                                   x∈R1

+— |sh(at) | + 4— 2 p= Jsh(2atp2) — p2sh(2at)| sup |^(x)|, t G R¹.

Замечание 1. Хотя изначально ставилась цель найти решение u(x,t) линейного однородного уравнения изгибных колебаний на полуоси t € R-, формула (18) определяет u(x,t) на всей числовой прямой t € R¹, что естественно вытекает и из самого задания уравнения, так как оно не меняется при замене t ^ —t.

Замечание 2. Так как классическое решение V(t) абстрактной задачи Коши (16), (17) принадлежит C ⁽²⁾(R-; C [R¹]) и для него GV (t) € C (R1-; C [R¹]), то значения решения u(x,t) = (I — d²/dx²) 1V (t) уравнения (3) принадлежат C ⁽⁴⁾[R1] для всех t € R-.

• 3.    Локальное решение задачи Коши для нелинейного уравнения изгибных волн

Применив к обеим частям уравнения (1) линейный ограниченный оператор (I — d²/dx²) , получим эквивалентное (1) нелинейное интегро-дифференциальное уравнение — нелокальное уравнение Клейна — Гордона:

u_tt — a² u_xx = a²u — ви³ + h * (ви³ — a²u).                    (19)

Уравнение (19) в пространстве C [R¹] можно записать в виде абстрактного полулинейного уравнения

V tt = GV + F (V), t € R-, (20)

где оператор G такой же, как и в уравнении (16), а F (V) — заданный нелинейный оператор. действующий в пространстве C [R¹]: F (g) = в[(I — d²/dx²)-¹ — I ]Q(g). здесь Q - оператор суперпозиции: Q(g) = f (g(x)), g(x) € C [R¹], f (s) = s³.

Отметим, что из непрерывной дифференцируемости оператора суперпозиции Q в пространстве непрерывных функций [8, с. 406] и ограниченности линейного оператора (I — d²/dx²)^-1 — I следует непрерывная дифференцируемость по Фреше нелинейного оператора F (V) в пространстве C [R¹].

Из непрерывной дифференцируемости отображения F (V) следует, что F (V) удовлетворяет локальному условию Липшица. Поэтому существует промежуток [0,t*[, в котором задача Коши (20), (17) имеет [9, с. 87] единственное обобщенное решение V = V(t), т. е. единственное непрерывно дифференцируемое решение интегрального уравнения

t

V (t) = C (t; G)Ф +

S(t; G')Ф + У о

S(t — т ; G)F (V(т)) dT,

t € R-,

для любых Ф € D (G) 11 Ф € C1[R1 ].

Применяя оценки (13), (15) норм оператор-функций (12), (14), записанные, используя элементарные неравенства. sh(t)sh(т) 6 ch(t + т)/2. |sh(t)| 6 ch(t). t,т € R1. в виде kC(t; G) k 6 ^ch(2atV2) = p(a,t). kS(t; G) k 6 P^. и учитывая, что для элементов пространства C[R1] справедливо соотношение Ц ФФkC 6 ||Фкс|| ФkC. в силу него, с ним можно работать как с алгеброй [10, с. 120], из интегрального уравнения (21), учитывая оттенку ch(t — т) 6 ch(t)ch(т). выводим интегральное неравенство kV(t)kC 6 P(a,t) ^(a, ф ф) +

|β| aV2

t j ch(2aтV2)kV(т)kCdT , о

t € R-,

где H(a, Ф, Ф) = ||Фкс + 1/(2aV2)kФ||c- Из неравенства (22) следует [11, с. 13] оценка нормы обобщенного решения kV(t)|c 6 H(a,Ф,^p(a,t)(1 - q(a,e)^2(a,ф, W(a,t)) 2, где 6(a,t) = 3atV2 + sh(4atV2) + sh(8atV2) /8. на времен!юм отрезке t Е [0,t*]. длина, которого ограничивается величиной t* = sup{t Е [0,t*[: 6(a,t) < 1/(q(a,e)H2(a, Ф, Ф))} Здесь q(a,e) = |в|(2a2 + 1)3/(64a8).

Итак, на отрезке [0, t*] существует обобщенное решение абстрактной задачи Коши (20), (17), для которого справедлива оценка, нормы (22). Это обобщенное решение V(t), t Е [0,t*], будет классическим решением задачи Коши (20), (17), если оно дважды непрерывно дифференцируемо по t, что является следствием [9, с. 91] непрерывной дифференцируемости по Фреше нелинейного оператора F(V), при условии Ф Е D(G) л Ф Е C1[R1],

Таким образом, имеет место

Теорема 2. Пусть начальные функции y(x), ^(x) задачи Коши (1), (2) принадлежат пространству C[R¹] вместе со своими производными до четвертого порядка включительно ⁷. тогла при t Е [0, t*]. где

64a8 t*=supГ: (a,t) < ie^+w^ay^yI,

^^У,^) = sup Их)| + -—= suP Mx)!, xeR1          2av 2 xeR1

существует единственное классическое решение u = u(x, t), (x, t) Е R¹ x [0, t* ], этой задачи в пространстве C[R¹], для которого справедлива оценка

1                                   |в |(2a2 + 1)3 Q2(a,y,C)r/ ,    1

sup |u(x, t)| 6 x ∈ R¹

1 + д-^-) H^ty^ch^oitV2) 1--—--------d(a,t)

2a2                                      64a8

• 4.    Существование глобального решения уравнения изгибных волн и разрушение его решения на конечном отрезке

Как известно [12], если функция g(x), принадлежащая пространству C[R¹], также принадлежит пространству Соболева. W^R¹). т. о. g(x),g⁰(x) Е L₂(R¹). то справедлива оценка.

+∞ kgkc = sup |g(x)| 6 kgkw1 = x∈R1                 2

j [⁽g^{(x))2 + (}g^0(x))2]

dx,

-∞ причем, если к тому же g(x) Е C (2)[R1], то пре дел при x ^ ±то функций g(x), g0 (x) равен нулю.

Полагая, что для всех t > 0 классическое решение u = u(x,t) уравнения (1) принадлежит перееенешпо пространств C [R¹] П W21(R1). исследуем так называемый интеграл энергии

+∞

y^(t) = kukWi = у cu²⁺ux) dx,

-∞ в котором u = u(x,t) — решение уравнения (1).

Применяя к равенству y⁰(t) = 2(u,u_t) + 2(ux,u_xt) неравенство Кош ii - Буняковского⁸ и используя элементарное неравенство 2ab 6 a² + b², выводим оценку

y⁰(t) 6 hi2 + kuxk2 + ku t k2 + kuxtk2,

из которой, обозначая z(t) = ||ut || W21 = ||utk2 + ||uxtk2, имеем

y'^{(t) 6} y^{(t) + z(t)}.

Аналогично из равенства, [y⁰(t)]² = 4[(u,u_t)² + 2(u,u_t )(u x ,u_xt) + (ux,u_xt)²] получаем оценку

[y0(t)]2 6 4y(t)z(t).

Используя уравнение (1), представление u_xu_xtt = (uu_xtt )_х частям, из соотношения

- uuxxtt

+∞

+∞

2 y⁰⁰(t) = j u2 dx + У u Xt dx — в У uX dx - a² У uXx dx

-∞

-∞

-∞

-∞

выводим первое энергетическое равенство

2 yo0(t) = z(t) - ^ux^

-

a2 lluxx^2-

uxtuxtt частям, из представления производной z0(t):

= (u t U xtt )_x

- utuxxtt

+∞

- β   u4 dx

4x

-∞

-

α2    u2xx dx ,

-∞

следует второе энергетическое равенство

z(t) = So - 2в kuxk2

-

α kuxx k2,

где So = H|W + а2|Д0k2 + e||(Д)212.

Пусть в уравнении (1) параметр в > 0. Тогда из соотношений (23) и (26) следует, что

У0(т ) 6 у(т) + S0. т > 0. II. значит, по лемме Гронуолла

y(t) 6 [y(0) + tSo] et,    t >  0.

Из неравенства (27) следует, что при выполнении начальными функциями ^(x), ^(x)

Щ),Щ) е ИДМ); W(x)fM (x) e L2 (R1),             Os)

классическое решение u = u(x,t) уравнения (1) принадлежит пространству Соболева W21 (R1) и, значит, справедлива оценка sup |u(x,t) | 6 x∈R1

+∞

У [(u(x,t))2 + (ux(x,t))2]

-∞

dx 6 рУ(0) + tSo e ²,

t >  0,

обеспечивающая существование глобального решения уравнения (1).

Таким образом, имеет место

Теорема 3. Пусть в уравнении (1) параметр в > 0. а иачальиью функции ^(x) ^(x) удовлетворяют условию (28). Тогда, существует единственное глобальное классическое решение задачи Коши (1), (2), для которого справедлива оценка (29) или в подробной записи sup x∈R1

Hx,t)| 6 У IMW+ t (k^kWi+ а2 1ин2+ 2 и(^0 )2k2) e2,

t >  0.

Исключая из энергетических равенств (25), (26) слагаемое с параметром в, имеем y^M(t) — 6z(t) + 4S_o = 2a2ku_xxk2, откуда, в силу оценки (24), вытекает дифференциальное неравенство для интеграла, энергии

y(t)y00(t) — |[y0(t)]2+ 4Soy(t) > 0(30)

Сравнивая (30) с основным дифференциальным неравенством для интеграла энергии из [13], заключаем, что если потребовать выполнение условий k^kw1 > 0, M ^^НО/,f) > 0, So

то имеет место

оценка снизу интеграла энергии: y(t) > (IMI

-1/2

W21

- Nt

—2

, и оценка сверху

времени T* существования классического решения уравнения (1):

T* 6 N—11И|Д, тле N = k^kW)/2^M2 — SoH^kWi.

Таким образом, имеет место

Теорема 4. Пусть параметры а, в и начальные функции у (x), ^(x) задачи Коши (1), (2) подчинены условиям (31). Тогда, не существует глобального по времени классического решения уравнения изгибных колебаний нелинейно-упругого стержня, т. е. решение разрушается за конечное время T*, причем имеет место оценка (32) для времени существования решения.

Замечание 3. Оценку (29) можно существенно улучшить, если воспользоваться при в > 0 неравенствами, вытекающими из энергетических равенств (25) и (26): 1/ly⁰⁰(t) 6 z(t) 6 So- откуда, шгтегрируя. имеем y(t) 6 y(0) + y⁰(0)t + Sot².