Задача линейного программирования со случайными входными данными

Задачи оптимизации в конечномерных пространствах могут быть охарактеризованы некоторым числом фиксированных входных параметров, которые определяют ее структуру и методы решения. В задачах линейного программирования такими фиксированными параметрами являются коэффициенты целевой функции, матрицы ограничений и правых частей ограничений. Решение таких оптимизационных задач состоит в поиске оптимального решения для заданных входных фиксированных параметров.

Входные данные моделей линейного программирования часто точно неизвестны или (и) носят случайный характер. В этих условиях для целей моделирования нередко берутся «средние» величины коэффициентов, а далее получается некоторое решение, оптимальное в данной модели, но которое не всегда является оптимальным в исходной задаче [1].

Одним из подходов, который работает с неточными коэффициентами в задачах линейного программирования и «пытается встроить» влияние неточности коэффициентов в модель, является стохастическое линейное программирование. Прогресс в этой области начался в 1960-е и 1970-е гг. и связан с именами Дж. Уэтса, А. Прекопа и К. Кала.

Существующие подходы и методы стохастического программирования имеют определенные недостатки. Прежде всего, это связано с численным преобразованием задачи стохастического линейного программирования в детерминированную задачу нелинейного программирования. Хорошо известен тот факт, что алгоритмы нелинейного программирования на практике применимы к задачам с относительно небольшой размерностью [1].

В тех случаях, когда известны функции плотности вероятности для стохастических данных, можно с успехом использовать метод Монте–Карло [2].

При всех его положительных качествах этот метод обладает рядом недостатков. Одни из самых существенных — низкая скорость сходимости и большой объем вычислений.

В статье рассматривается численный метод решения задачи линейного программирования со случайными входными данными, основанный на численном вероятностном анализе, предметом которого является решение различных задач со стохастическими неопределенностями в данных с использованием численных операций над плотностями вероятностей случайных величин и функций со случайными аргументами. Такие задачи, как правило, характеризуются высоким уровнем неопределенности своих показателей и отсутствием необходимой информации о них.

Постановка задачи

Сформулируем общую задачу линейного программирования со случайными данными в следующем виде:

(c, x) ^ min,

Ax=b,x>0,(2)

А g A, b g b, c g c, где A - случайная матрица, b, c - случайные векторы размерности n .

Точка x * - решение задачи (1) - (2), если

(c, x *= inf( c, x ), где

U = {x | Ax = b, x >  0}.

Множество решений (1) - (3) определим следующим образом:

X = { x | ( c , x ) ^ min , А = b , x >  0 , А g A , b g b , c g c } .

Заметим, что x * - случайный вектор, поэтому в отличие от детерминированной задачи для x * необходимо определять функции плотности вероятности для каждой компоненты x * как совместную плотность вероятности.

Расширим отношение порядка * g { <,<,>,> } на случайные переменные:

x * у о x * у для всех x g x , у g у .

Если носители x , у пересекаются, можно говорить о вероятности x * у :

P ( x * у ) J = ( x , у ) dxdy ,

Q где Q {(x, у) | x * у}, p(x, у) - совместная плотность вероятности x, у .

Известно, что x * достигается в угловой точке множества U .

Теорема 1 . [3] Пусть множество U определено условиями (5), Для того чтобы точка x = ( x 1 ,..., x_n ) g U была угловой, необходимо и достаточно существование номеров J 1 ,... j_r:

A_;x_; +...+= A_;x_; b ;= 0 , j * j ,= 1 ,..., r ,

J\ J\                Jr Jr        j j причем столбцы Aj ,..., Aj линейно независимы.

Пример 1. Пусть U определяется матрицей А и вектором b :

<113 1)<

А =               , b = ,

(1 -1 1 2)( тогда столбцам матрицы А1, А2 соответствует угловая точка с координатами (2, 1, 0, 0), А1, А3 - (0, 0, 1, 0), А2, А4 - (0,5/7, 0,4/3).

Заметим, что из n столбцов можно выбрать r линейно независимых не более чем C n способами. Следовательно, число угловых точек множества U конечно.

Это значит, что каноническую задачу (1)-(2) можно попытаться решить следующим образом:

• 1)    найти все угловые точки x множества U ;

• 2)    вычислить значение функции ( c , x ) в каждой из угловых точек и определить наименьшее из них.

Однако такой подход практически не применяется, так как даже в задачах не очень большой размерности число угловых точек может быть очень большим. Тем не менее идея перебора угловых точек множества U оказалась весьма плодотворной и послужила основой ряда методов решения задач линейного программирования. Одним из таких методов является симплекс метод [3].

Решение задачи случайного линейного программирования

Для задачи (1)-(3) построим совместную плотность вероятности вектора x * . Для этой цели воспользуемся одним из способов решения детерминированных задач линейного программирования, например симплекс методом.

Рассмотрим вспомогательную задачу:

(ct, x) ^ min,

AtX=bt,x>0,(5)

AteA,bteb,Ctec.(6)

Для нее найдем решение x * и соответствующую ему угловую точку с номерами j 1 ,... j_r . Решим случайную систему линейных алгебраических уравнений [4]:

⁽ A _к- A j r ) x = b.

Совместная плотность вероятности найденного решения будет соответствовать _x* . Если носители входных параметров достаточно малы, то _x* будет совпадать с x* . В случае произвольных носителей входных параметров процедуру выбора A_t e A,b_t e b,c_t e c следует повторить, используя подходы метода Монте–Карло или генетических алгоритмов. Если при этом будут получены разные решения _x* , то их можно сравнить, вычисляя вероятностные расширения целевой функции f _t = ( c , _x * ) [5].

Численный пример

В качестве численного примера рассмотрим следующую задачу:

(c, x) ^ min,

Ax=b, x>0,(8)

A g A, b g b, c g c, где A = (a j) - равномерная случайная матрица, каждый элемент такой матрицы - равномерная случайная величина с носителем [a j, aj];

• b , c - равномерные случайные вектора.

Носители заданы следующим образом:

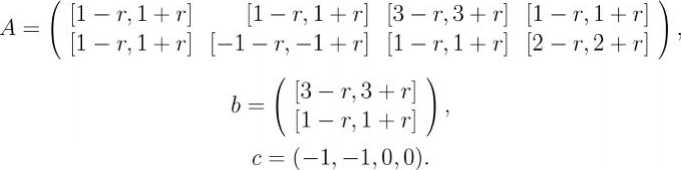
При r = 0, что соответствует детерминированному случаю, x *= (2 , 1 , 0 , 0), столбцы матрицы A 1 , A 2 соответствуют угловой точке.

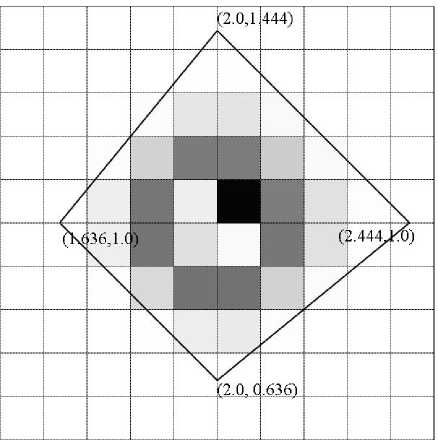
Рис. 1. Совместная плотность вероятности вектора решения на плоскости ( x 1 , x 2 )

На рисунке 1 приведена совместная плотность вероятности вектора ( x 1 , x 2 ) при r = 0 . 1, компоненты x 3 = 0 , x 4 = 0. Сплошная линия - граница множества решений на плоскости ( x 1 , x ₂). Множество решений X - четырехугольник с вершинами (2.0,0.636), (2.444,1.0), (2.0,1.444), (1.636,1.0). Как видно из рисунка, плотность вероятности распределена крайне неравномерно, самая большая в центре, в окрестности точки (2.0, 1.0).

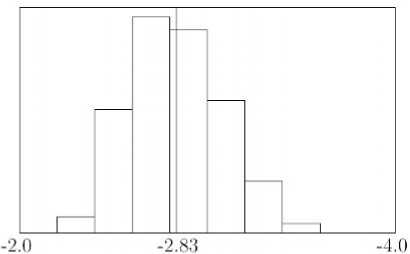
Рис. 2. Гистограмма целевой функции

На рисунке 2 приведена гистограмма целевой функции c 1 x 1 + c ₂ x ₂, математическое ожидание целевой функции в точке –2.834.

Площадь области X сильно зависит от величины r . С увеличением r она растет и уже при r = 1 становится бесконечной. Это определено тем, что среди матриц

/ о 0 X    / [0,2]    [0.2] \

0 о / \ [0,2] [-2.0] ) есть линейно зависимые столбцы.

Заключение

С целью снижения уровня неопределенности входных параметров задачи линейного программирования и повышения эффективности численных процедур метода в рамках численного вероятностного анализа применяется подход, реализующий идею использования гистограммных, вероятностных и естественных расширений для представления функций плотности вероятностей случайных величин.

Показана эффективность использования численного вероятностного анализа для решения задач линейного программирования со случайными данными. Метод основан на нахождении угловых точек и решении соответствующих им случайных систем линейных алгебраических уравнений. Приведенный пример показывает, что данный метод позволяет на основе численного и визуального представления совместной плотности распределения определить границы множества решений на плоскости ( x ₁ , x ₂), а также получить информацию о характере распределения вектора решений и его наиболее (наименее) вероятных значениях, что существенно повышает качество анализа возможных решений рассматриваемой задачи.