Задача Маркушевича в классе автоморфных функций в случае произвольной окружности

• 1.    Постановка задачи

• 2.    Решение задачи Маркушевича

Пусть Г: cr₀(z) = z, o_k^z\ £ = 1,2,... - конечнопорожденная фуксова группа второго рода, оо - обыкновенная точка группы. Очевидно Г* =Т°Г°Т, где Т \z* = z₀ + r₀² i^z-z^ - преобразование симметрии относительно главной окружности Ц . Известно, что такая группа является группой дробно-линейных преобразований первого класса [4]. Пусть Rq - фундаментальная область Форда, р - род фундаментальной области, S - область инвариантности группы, D_± - соответственно внутренность и внешность главной окружности, R_±=R_or>D_±, L, - множество дуг главной окружности, получаемой из L удалением всех предельных точек группы.

Задача Маркушевича в классе автоморфных функций ставится следующим образом: требуется определить кусочно-аналитическую, автоморфную относительно группы дробно-линейных преобразований Г функцию ^(z), если на контуре Lq = L о Rq ее краевые значения связаны соотношением

Ф₊ (Z) = a(t>_ (Z) + b(t)ip₊ (t) + /(f),                              (1)

где a(f), b(f) и /(Z) удовлетворяют условию Гельдера, a(z)*0, Z>(Z)*O, 6(Z) +1 ^ О, функция a(Z)/(/>(Z) +1) аналитически продолжима в область D_ и автоморфна относительно Г в области D_ . Если /(Z) = 0, то имеем однородную задачу Маркушевича. Решение ищется в классе функций, исчезающих на бесконечности.

Перепишем (1) в виде

⁽²⁾ Z>(z) + 1          Z>(z) + 1               b(t) + X

• и, считая Re^/₊(Z) известной, рассмотрим соотношение (2) как краевое условие задачи Римана в классе автоморфных функций относительно группы Г. Тогда ее решение относительно функции

( фДг), если zeD₊, a(z) / з            п

—ф_ (z), если z g D_ Z>(z) + 1

определится формулой [5]

ОД=~ if                           + У c_k£_k(z,«) + c₀ ,        (3)

2ni Ь(т) +1            Ь(т) + 1)

Математика

, х                       f к, если |Z>(7)|<1,/б£п, к = Ind, a(t\ кх^ Ind. UAt^ X V к( = ^------= s

¹               ’ ^{0 k} b^ + \           если 16(7) |>l,?eZ₀.

Автоморфный аналог ядра Коши J(z,r) имеет вид [3]

A(z, т) = K(z, т) - ^ (t)K(z, о, ) -... - сор (т^К (z, ар ), р - род фундаментальной области Ro ,

”   cr,'(r)

i

fy^r-ajiz) T-or_y(oo)J’

№r) = 2   V-

™‘0

^k(z,oo) = / + ^ ^j (z) - o^k

Р to^k *(оо)

V —-----K(z,aA, к = 1,...,к₀

являются коэффициентами разложения ядра A(z, т) в окрестности т = оо. В точках aj gRq\L₀, Oj *z₀, j = \,...,p и в точках, конгруэнтным им, функция ^(z,oo) имеет простые полюсы. Подберем числа с_к таким образом, чтобы вычеты функции Q(z) в точках a^j = \,...,р, были равны нулю, что обеспечит аналитичность функции в этих точках. То есть должны выполняться равенства:

_ 1 Г Г 2Z)(r) / c_kd, _k —--I ------- ы ^Л 2»^ад+1

Rey/+(r) +

/(Г)

6(т) + 1

СоДтУт, j = \,

2тР

r 26(r)            /(т)

/ Ь(т) +1           b(j^ +1

A)

toj^dr = 0, j = 1,

Если г (0 < г< min{/),/c₀ -1}) - ранг матрицы коэффициентов системы (4), то при выполнении этих условий разрешимости решение зависит от к₀ - г произвольных постоянных над полем С.

На основании формул Сохоцкого из равенства (3) имеем на контуре L_o

^(0 = — J

2.Л1 ;

Ч)

^~т^е<рДт) + Ь(т) +1

/(г)

Z>(r) +1

A(z,T)dr +

b

С другой стороны, заметим, что функция vp₊ (z) определяется в области R₊ с точностью до мнимого постоянного через значение своей действительной части на контуре Lq [2]:

ip₊(z)- — J Re^^T)^(z,T)<^T + 2y yy_K(z,<2,)-/?-Hc,

Р = ~ ^Кеу^А^т^т, Yj=— jRe^₊(T)<9_y(r)j = L

Ч)

если выполняются p условий разрешимости

2p,

J Re^₊(r) ®Дт) +

Ц L

(oj-zof

^-zof

Юр+р) dr = Q, j = \,...,p.

Точки QjJ = X,..., р выбираем таким образом, чтобы выполнялись равенства *      *           г²

ap+j = Qj ’ °j* = z0 + —°™, j ^,2,-.,Р.

Тогда из соотношения (7) имеем на контуре L_Q

1г                  2/7

у/₊(0 - Re^₊(0 ⁴—; J Re^₊(r)^(z,T)Jr + 2^ yjK^t^p-P-v ic.

7=1

Следовательно, на основании формул (6), (9) приходим к сингулярному интегральному уравнению

WPP 1 г Rey<₊(r) _  /(/)

6(0 + 1 Tri) Ь(т) + \      ^;     2(6(Z) + 1)

I             Е сб^(г°°)+«(0+^

2тп Д Ь(т) + \

2р d = P-ic + cQ, ait^-l^yjKit^j).

Здесь Rei/л (/ ) должна удовлетворять р комплексным условиям разрешимости (8). Для однозначной кусочно-голоморфной функции

1 г 2Re^ (г)-/(т) ^{y + v} ■ A(z, zAdr 2тл /     6(т) +1

приходим к односторонней краевой задаче для автоморфных функций, решение которой записывается в виде [1]

W) =

к0-1

T«ck^z^*a

6=1

(Ю)

Ф (z),

Z £ D_, где ср"^ - произвольная аналитическая, автоморфная относительно группы дробно-линейных преобразований Г функция в области D_, исчезающая на бесконечности. На основании (10) имеем

Reip,(t) Ir^¹_x           /(0

"^^ = 3V^c^k

6(0 + 1 2 “                  6(0 + 1

Учитывая, что в левой части выражения (И) имеется функция Re^+(0, приходим для функции

к краевой задаче Гильберта в классе автоморфных относительно группы Г функций:

Re{-/[6(Z) + 1> (Z)} = Im (6(0 + 1)* d + a(t)+ ^         +

k=\                    + \

Каноническая функция данной задачи, удовлетворяющая краевому условию, хЧО Kt)+i определится формулами [2]:

zGO=zo(zWA

_Zo(z) = e^rl^z^4z,<»,0_o)J^ 7=1              7=1

Xj = M, [6(0 + 1], T(z) = —^— ( AXz,T)ln(6(r) + l)<6r,

Z,0

cr_x(z\...,cr_n(z') - порождающие преобразования группы Г; 0_jeR_o\L_o, 0j*0_o, j = \,...,p, где 0_O - фиксированная точка области R/, m ,j = \,...,n - целые числа. Функция

Математика

е

E^z,0,9(y)-exp

^K{z,r)dT , 0_О е Rq\L₀

Л> J берется вдоль пути, целиком расположенного в 5. Она однозначна в этой области и в случае неконгруэнтных между собой точек 90 и 9 имеет в этих точках простой полюс и нуль кратности 1 соответственно. Если точки 90 и 9 между собою конгруэнтны, то £^,9,9^ на множестве S ограничена и нигде не обращается в нуль.

Так как 7₀(cr_A(z)) = Z₀^e^Hk,\/zgS\L, где

!                                     9j               р 9j               п

Н_к=-— ^П_к(.т)\п(Ь(т) + \^т-к_х ^_k(T)dr ^^т^т + ^т, J П_к(т^т, к = 1,2,..,

21711 Lq                                e0              7=1 e0              7=1 0O то для автоморфности канонической функции %(z) необходимо потребовать, чтобы все

Нк = 0 (mod 2/п). То есть целые числа mj,j-\,...,n и точки 9j gRq\L0, 9j ^9Q,j ~\,...,р опреде- z ляются из проблемы Якоби обращения интегралов

SVkI^еj) + Е^mj^Tlk,j + »k^i = -T— J Пк0")НШ)*\W*K_Xф_к0»\

7=1           7=1                        2711 Lq где nk, к = l,...,p - некоторые целые числа,

<7/(Ро)

9kj=^k(^CTj(^z))-z) = J 9к(тЖ j = l,...,«.

So

Функция /0(z) автоморфна относительно группы дробно-линейных преобразований Г, имеет в точках 9ь...,9т, образующих частное решение проблемы обращения Якоби, нули кратности

^,...,Л_т соответственно, а в точке 9₀ имеет порядок ^ - р.

Решение этой задачи запишется в виде [2]

-z^(z) = Z(Z)№) + ^^

где

Г c(t)

J [ft(r) + l]Z+«

Lo

1 Г с(т^

A^z, T)dz =--- ------------X-----K(z, T^dT -

2л-/ J [Z>(r) + 1]^ (r)

d f........-............--У——codT^di, j = \,...,p, Й ^{J j j} 2^/ J[6(r) ₊ l]_Z⁺(r) ⁷

т ^q

^=1 И=1

СЛ^ = Х j=0

(cry(z)-^r

(сг^со)-9дУ

Для того, чтобы краевая задача (12) имела решения в классе функций, исчезающих на бесконеч- ности, необходимо выполнение следующего условия:

f                   + С + 4^0) + ^(z0) = 0 .

^"QbW l]z ⁺(г)

Постоянные c_{q v}, c_v при к_х> р должны удовлетворять неоднородной системе линейных уравнений

9=1 v=l                  r0                      r=l                 r0

(5--zo)2

2 ^UP*p

F

в которой

J 4лг /

Lq

Z+(06(0 + 1

toj^dr.

Если к_х< p, то кроме системы (15), где все c_v = 0, должны выполняться еще р-к_х комплексных условий:

,у-1               -----------,                          ,/-1 г          --------- г ад*^*) I ^ЬрЬ^--— F^ + Fo^ \z^,j = \,...,p-Kx.   (16)

dz^J L                J                 dz^Jl              J

Известно [2], если к_х > p, k_q > 0, функция ф^ с учетом условия разрешимости (14) содержит 2аГ[ -2/? + 2х"₀ + 1 произвольных вещественных постоянных; если к_х< р, к₀ >0, то число этих постоянных равно Тр + 2к"₀ +1. При этом, если к_х< р, лг₀ > 0, то эти постоянные должны удовлетворять системе 2р-2к_х вещественных линейных уравнений (16). Система (16) неоднородна. Как известно, ее разрешимость эквивалентна выполнению следующих 2/7 -2к_х -г_х вещественных условий (Г[ - ранг матрицы системы (16)):

Р~КХ

У (и._k Reb.•' + и , Im6.') = 0, к = 1,...,2р-2к_х -г_х,

r0-l

ImU6(r) + l]   У с_к^(т,оо) + у(т) >

S14) = -^ J

4тп /

k=K'0-rl+l

A(z,T)d(r),

№)»№

y(r) = tz(T) + d + -^^-, b(r) +1

где p_{x k},...,p_{3p 2k k}, к = \...,2р-2к_х -г_х,- полная система линейно независимых решений соответствующей однородной транспонированной вещественной системы.

При выполнении этих условий, также учитывая условие разрешимости (14), задача Гильберта имеет решение, которое содержит 2рА-2к₀ +1-^ произвольных вещественных постоянных. Если г, = 2р + 2лг₀ +1, решение будет единственным.

Пусть теперь Kq<0. Тогда имеем: при к_х >р функция ^(z) содержит 2к_х -2/э + 1 произвольных вещественных постоянных, а при ^ < р число этих постоянных равно 2/7 + 1, если выполняются р комплексных условий (8). При этом, если к_х< р, то эти постоянные должны удов-

Математика

летворять неоднородной системе 2р-2к_х вещественных линейных уравнений (16). Разрешимость системы (16) эквивалентна выполнению следующих 2р - 2^ -Г] вещественных условий

^(^Re^+yU Im6) = 0, к = \,...,2р-2к_х-г_х,         (18)

где р_хк,...,ц_{гр к}, к = \,...,2р-2к_х -г_х - полная система линейно независимых решений соответствующей однородной транспонированной вещественной системы.

При выполнении этих условий, учитывая условие разрешимости (14), задача Гильберта имеет решение, которое содержит 2/70+1-Г! произвольных вещественных постоянных. Если Г] = 2/7 + 1, решение будет единственным.

На основании формул (11), (13) на контуре Zo имеем задачу Римана г0-1

⁺   КО+1

у ЛО* НО 2 Q^^-^OW +/W>(0-

4=1

-ад%"да^о+f^o+ад+ад+т, (/)+^ (/)]+

o(z) + l

Решение задачи (19) запишется в виде

2тп

jW) X Q^(n°°)+«(7)+tZ ^fAWV

4Z>(r)Z4r)mr) + F0+(r) + 4Vr^^

о(т) + 1

+с₀ + X ^Ск№<»\

Тогда общее решение неоднородной задачи Маркушевича определится формулой

Q(z),     z&D₊,

--------12yZJ, Z € L'_.

Условия разрешимости (4), (5), (8) в этом случае будут выглядеть следующим образом:

Г0-1                 ,             K-Q-1

£ ^ck^dj,k = -т— fWtXE c_fc^(T,«>) + o_:(T) + cZ + /(T)-i^"(T)[F₀"(T) +

4=1                   L_o k=\

+F0V) + 4Vr) + 4Vr) + ^(r) + 4Vr)]) + 7~^]®,W^^

Z>(r) + 1 v

— J 1Н0(а<Л)^{+d +}/(^r) - ^(т)[ЛГК)+Fq (t)+

+Ч'о(г) + ЗД + Ч'1(г) + ВД])+-^-]щу№г = О,у=:1,...,/7,^о<О, г [6(r) +1], v~t    „ ,    ,     , . , f(.A

--;--(E c4^(n=o) + «(r) + t/ + -7—7-

4Z4r)№) + № + ^0(r) + W^                    (23)

(a, -z₀) -------

.(T)]dT-0, ; = l,...,p.

K-z0)2

Таким образом, в случае | b(t) | < 1 (так как тогда к_х = 0, к_й=к), если к > 0, то неоднородная

Патрушев А.А.                          Задача Маркушевича в классе автоморфных функций

______________________________________________________в случае произвольной окружности задача Маркушевича имеет решение, которое содержит 2р + 2/г +1 - гх - 2г произвольных вещественных постоянных, если выполняются 2р-гх вещественных условий разрешимости (16), 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23) (гх -ранг матрицы коэффициентов вещественной системы (16), г - ранг матрицы коэффициентов системы (21)). Если к<0, в случае |6(Z)|<1, то задача имеет решение, которое зависит от 2р-гх+1 произвольных вещественных постоянных, если это решение, в свою очередь, удовлетворяет р комплексным условиям разрешимости (22) (при этом Ч^(z) = 0) и -к +1 условиям разрешимости

/м(оо) = 0,у = 0,...,-к- + 1,                                    (24)

где /^(оо) - коэффициенты разложения функции

J WXd + а(г) + /(т) - iz"(T)\_Fo (т) + Fy (г) +Т0(т) + Ч,0(т)]) + -~^-]Л(г, т^т ч> в ряд Лорана в окрестности бесконечно удаленной точки. То есть мы приходим к неоднородной системе линейных уравнений относительно 2р-гх +1 неизвестных, число же уравнений над полем R будет 2/Э-2/С + 2. Полученная система будет разрешима лишь при выполнении 2р - 2к + 2 - г2 необходимых и достаточных условий

2Д-21С+2

2 А./Л =0, Z = l,...,2^-2r + 2-r2,                    (25)

k=\ где Р\р...,Р1р-гк*гь I -^---Др-^к + 2-г2 - полная система линейно независимых решений соответствующей однородной транспонированной системы, г2 - ранг матрицы коэффициентов системы, полученной объединением систем (21), (22)

У к = 7" / №)№) + d + f^ - I^CtW (т) + Fq (т) +

+^0 (т) + Т_о (г)]) +                  к =1,..р,

о(т) + 1

УгР^р\= !кЙ^. j = 0,.--K + V

В случае |Z>(0| > Ъ к₀>0, к_х> р, неоднородная задача содержит 2к-2р-2г + 1 произвольных вещественных постоянных, если выполняются 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23). Если же | Ъ^ | > 1, к₀ > 0, к_х< р, то задача имеет решение, которое содержит 2р + 2к-₀ - 2r +1 - г_х произвольных вещественных постоянных, если выполняются 2р-2к_х-г_х вещественных условий (17), 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23).

Рассмотрим теперь случай | b^ | > 1, к₀< 0, к_х > р. Неоднородная задача имеет решение, которое линейно зависит от 2к_х -2р + 1 произвольных вещественных постоянных, если выполняются 2р вещественных условий разрешимости (23), 2р вещественных условий разрешимости (22) и -к_й +1 условий

/^\оо) = 0,у = 0,...,-к-0 + 1,                                    (26)

где /(у\°о) - коэффициенты разложения функции

J IMrXd + а(т) + /(г) - ^"(HlX (^г) + ^ (^г) + Аз

+Т₀ (г) + Ч^?) + Yi (г) + Ч^]) +         туг

о(т) +1

в ряд Лорана в окрестности бесконечно удаленной точки. Следовательно, мы приходим к неод-

Математика

нородной системе уравнений относительно 2^-2/9 + 1 вещественных неизвестных, число же уравнений равно 4/?-2л;0 + 2. Полученная система будет разрешима лишь при выполнении 2/9 - 2/с0 + 2 - г3 необходимых и достаточных условий

2/7-2г0+2

X А,/Л=О,7 = 1,...,2р-2^о+2-г3,                  (27)

к=\ где Д              ^ = 1,-",2/7-2к"0+ 2-г3 - полная система линейно независимых решений соответствующей однородной транспонированной системы, г3 - ранг матрицы коэффициентов вещественной системы (22), (26),

Ук = “ J VWW) + d + /(г) - 1%Чт(\Н7 ^ + Fg (т) +

+4Vr) + W + 4'₁(r) + ^]) + -^^>_t(^ к = \,...,р,

о(т) + 1

У_Р*^\ =/^и)(оо),у = 0,...,-/с₀+1.

И, следовательно, неоднородная задача в случае 16(f) | > 1, к₀< 0, к_х > р имеет решение, которое линейно зависит от 2к_х -2/7 + 1 -г₃ произвольных вещественных постоянных, если выполняются 4/9 —2/с₀ + 2-г₃ вещественных условий разрешимости (27) и 2р вещественных условий разрешимости (23).

В случае | b(t) \>1, к₀<0, к_х< р задача при выполнении 2/9 - 2к_х - г_х условий разрешимости (17) имеет решение, которое линейно зависит от 2р-г_х +1 произвольных вещественных постоянных, если это решение, в свою очередь, удовлетворяет 4/7-2(к:-/с_]) + 2 вещественным условиям разрешимости объединенной системы (22), (24), где 4^,₁(z) = 0 и 2/7 вещественных условий разрешимости (23). Произведя аналогичные выкладки, как и в случае | bit) |< 1, к< 0, имеем, что неоднородная задача в случае 16(f) | > 1, к₀< 0, к_х< р имеет решение, которое линейно зависит от 2/9-Г] -г₂ +1 произвольных вещественных постоянных, если выполняются 4р-2к_х-г_х вещественных условий разрешимости (17), 2р вещественных условий разрешимости (23) и 4/9 - 2(к* -/q) - г₂ + 2 вещественных условий (25), где г₂ - ранг матрицы коэффициентов вещественной объединенной системы (21), (24).

В итоге справедлива

Теорема. Пусть коэффициенты a(f), b^, /(f) g H(Lg), a(t) * 0, b(t) * 0, b(t) +1 ^ 0, f g L_o неоднородной задачи Маркушевича такие, что функция a(t)/{b(t) + \) аналитически продолжи-ма с контура Lg, лежащего в фундаментальной области Fg группы преобразований Г, в область D_ и автоморфна относительно Г в D_. Тогда неоднородная задача в классе автоморфных функций относительно группы Г ;

• 1)    при к>0, |6(f)| < 1 имеет решение, которое содержит 2р + 2к-2г-г_х произвольных вещественных постоянных, если выполняются 2р — г_х вещественных условий разрешимости (16), 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23) (р - род фундаментальной области, г_х - ранг матрицы коэффициентов вещественной системы (16), г - ранг матрицы коэффициентов вещественной системы (25));

• 2)    при к<0, 16(f) | < 1 задача имеет решение, которое линейно зависит от 2р-г_х-г₂ произвольных вещественных постоянных, если выполняются 2р вещественных условий разрешимости (23), 2р-г_х вещественных условий разрешимости (16), 4р-2кА-2-г₂ вещественных условий разрешимости (25) (г₂ -ранг матрицы коэффициентов вещественной объединенной системы (22), (24));

• 3)    при к₀ >0, к_х > р, |6(f)| > 1 имеет решение, которое линейно зависит от 2к-2р-2г

Патрушев А.А.                          Задача Маркушевича в классе автоморфных функций

________________________________________________________в случае произвольной окружности произвольных вещественных постоянных, если выполняются 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23);

• 4)    при k₀>Q, к_х<р, |А(/Д>1 имеет решение, которое линейно зависит от 2к₀ + 2р-2г -г_х произвольных вещественных постоянных, если выполняются 4р-2к_х-г_х вещественных условий (16), 2р вещественных условий разрешимости (21) и 2р вещественных условий разрешимости (23);

• 5)    при к₀<0, к_х>р, |6(/)|>1 имеет решение, которое линейно зависит от 2к_х-2р-г₃ произвольных вещественных постоянных, если выполняются 4р — 2к₀ + 2 — г₃ вещественных условий разрешимости (27) (г₃ -ранг матрицы коэффициентов вещественной объединенной системы (22), (26)) и 2р вещественных условий разрешимости (23);

• 6)    при Kq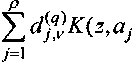 к_х<р, |6(Z)|>1 имеет решение, которое линейно зависит от 2р-г_х-г₂ произвольных вещественных постоянных, если выполняются 4р-2к_х-г_х вещественных условий разрешимости (17), 2р вещественных условий разрешимости (23) и 4р-2(к-к_х)-г₂ + 2 вещественных условий (25) (г₂ - ранг матрицы коэффициентов вещественной объединенной системы (22), (24)).