Задача моделирования коррелированных многомерных данных

Автор: Ширкунова К.С., Кокин И.В.

Рубрика: Естественные и технические науки

Статья в выпуске: 7 (16), 2018 года.

Бесплатный доступ

Данная статья посвящена рассмотрению задачи моделирования многомерных данных. Данные при этом являются коррелированными, следовательно, моделирование проводится с учетом вектора средних и ковариационной матрицы. Также смоделированные данные должны иметь аналогичное распределение. Анализ смоделированных данных проводится с помощью методов машинного обучения.

Машинное обучение, ковариационная матрица, печатные платы, моделирование данных

Короткий адрес: https://sciup.org/140263762

IDR: 140263762

Текст научной статьи Задача моделирования коррелированных многомерных данных

Технической диагностикой называется наука о распознавании состояния технической системы. Техническая диагностика решает обширный круг задач, многие из которых являются смежными с задачами других научных дисциплин.

Основной задачей технической диагностики является распознавание состояния технической системы в условиях ограниченной информации.

При решении основной задачи технической диагностики объекта с применением машинного обучения проводится бинарная классификация состояния объекта: объекты подразделяются на исправные и неисправные с помощью моделей, полученным по обучающим выборкам. Качество классификации, которое определяет эффективность машинного обучения, зависит от ряда факторов: объема исходной выборки, метода машинного обучения, способа разделения выборки на обучающую и контрольную части, отбора значимых показателей и других.

Однако, в некоторых ситуациях, объем выборок далек от необходимого числа данных. Например, для качественного машинного обучения требуется более 1000 данных по всем исследуемым показателям и далеко не каждое производство производит такое количество замеров при контроле качества.

Рассмотрим производство печатных плат, в ходе которого сточные воды загрязняются химическими веществами (кислотно-щелочной баланс pH, аммиак NH 4 , нитриты NO 2 , фосфаты P, железо Fe, медь Cu и нефтепродукты). Мониторинг химического состава сточных вод производится 2-3 раза в неделю в контрольной точке (канализационном колодце). При мониторинге необходимо следить не только за неожиданными выбросами (резким повышением или понижением концентрации вещества в воде), но и за допустимыми концентрациями каждого вещества (для рН – 8 мг/л, NH – 100, NO – 0,5, P – 1,1, Fe – 2, Cu – 0,05, н/прод – 0,7).

При этом, по результатам замеров за 2 года наблюдений имеется около 200 данных по каждому из 7 показателей химического состава, что явно недостаточно для машинного обучения. Поэтому встает задача о моделировании данных с распределением, аналогичным исходным данным, а также с соответствующим вектором средних и ковариационной матрицей.

Для моделирования многомерных данных обладающих свойствами реальных многомерных статистических данных нельзя использовать несколько раз процедуры моделирования одномерных данных, потому что в этом случае будут созданы независимые признаки и совместный анализ таких данных теряет смысл.

Многомерная совместная нормальная функция плотности является обобщением двумерного случая. Для многомерной случайной величины f = (f1, ^,fm) многомерная нормальная плотность определяется по формуле:

f(fi.....fm) = (2л-)т/2 |^|1/2 еХР(- 2 (f — Й^ — ^ — A)

где f = (f1, ^,fm) - многомерная случайная величина, которая математически представляет собой вектор-столбец:

! - вектором математических ожиданий многомерной случайной величины I :

-Г) Цт/

(I — j!) - разность двух векторов дает вектор-столбец:

I.pv'')

' ^ т ^Ц т'

В результате выполнения операции транспонирования получим вектор- строку

(f ^—!) = ^[|1 ^— Ml, -Лт

—

М т ]

2 - ковариационная матрица:

/ а^

2 = ( ^а 2 ² 1 ^а т1

где ^а 2 = M[⁽^_q ^— M_q)⁽^_t ^— M_t)] ,

^а 22

гт2

^а т2

а1т \ а2т атт/

q =1,2,3,... m , t =1,2,3,^, m ; (а^-а т™ ) -

диагональные элементы представляют собой дисперсии признаков; m - размерность многомерной случайной величины (количество признаков);

Вектор f = (fi, ^,^_т) произвольной нормально распределенной случайной величины можно получить специальным линейным преобразованием вектораM = (Mi, ^,М_т) , компоненты которого есть независимые нормально распределенные случайные величины с параметрами, ц = 0, а = 1 .

Преобразование п в ^ производится по формуле:

<^ = Лту + !

В преобразовании участвует некоторая треугольная матрица A:

/ 0-110

I °21

\ °mi omm

Коэффициенты aij могут быть определены с помощью рекуррентной процедуры. Общая рекуррентная формула имеет вид:

^o qt

—

2 r=1 ° qr ° tr

VOt"

у t-1 ^r=1

² ^o tr

где индексы изменяются в диапазоне 1≤t≤q≤m, а суммы с верхним нулевым приделом равны нулю.

Рассмотрим описанный выше алгоритм моделирования данных. Пусть имеется 159 значений по 7 показателям качества. Необходимо смоделировать еще 1041 значение по каждому из показателей.

Для начала необходимо вычислить вектор средних и ковариационную матрицу исходных данных (рис. 1 и рис. 2 соответственно). Все расчеты производятся в Excel.

вектор средних


7,842	72,11	0,395	0,915	1,577	0,022	0,285

Рис. 1. Вектор средних исходных данных

1		1 . •		4	1	*	7
1	оостов	•омом	61	\| ■■	0.10220	0.00007	6000*
2	0.200*	1126.» 1502	LhW	мет	МЛ17	o^uuv	U>l>M
1	61	i.nwi	ошм	6MW1	660027	600116	МХЫ1
4	босом	AM»»	A0W1I	6 04410	0.06161	AC00I1	6,00447
1	0 10020	617117	0,61021	606*1	гак»)	0,01771	0 00142
*	0 0000 7	Q.1MI7	600110	А00011	6017П	0.0010,	000017
	С 00000	1.01571	0.00007	600*7	0.001*2	600017	602М1

Рис. 2. Ковариационная матрица исходных данных

Далее необходимо сгенерировать вектор ту объемом 1041 х 7. Для этого воспользуемся пакетом «Анализ данных». Т.к. исходные данные не соответствуют нормальному распределению, то вектор ту будем генерировать при условии, что математическое ожидание и дисперсия этих векторов отличаются от 0 и 1, но достаточно близки к ним. Получаем произвольно сгенерированные столбцы вектора т (рис. 3).

ее*юр мормеленой<8 ЦлумеАми cre*^pnpoeeH««wAj

01	h2	л)	М	61	"6	*1
амты	» И 7*61174	А,1М5ЦШ	0,47461 И	0.11112051#	UH4M31D	1.0) 116411
O.WlM	М*7467Я	О^ЮТМОК»	L1162206	0,7107*0421	0,0150561)4	0.1425016»
0,107115	i_t 169*21644	0,170121ZJ7	L4204 7717	1,100157414	0,471611144	1.19)7452»
0.4ЭК1	0JJM01MI	О.17МММ5	0.064)1*0	ММ675.Ю	OJ191O7W1	0.5Ю00415
L7J6W	0,171199729	1,004110644	1,4/137*1	0.99 2 2964/1	1110452021	1.52911167
О.МЛ)	1_гМО2М0П	(1.124 900401	о.о mtn	0 54/4160 2 51	1,1195)7414	0.1610011
0.10W11	0.42/4141)	1,241649011	0.6191492	1.М41ХМЛ/	0^5615 mot >	134111446
0,1 токе	<МЮЛ2«Ю	0,111110175	0.55/41944	1,20214 НМ	1,0402/5/14	0..1ММЛ)
июли	0.412ЛИМ5	0,001503446	1,/еобО/4	1,001 МО 259	О, 744huew	2.14012544
l,0J 1М	MIDMII1	2,14206 ИИ/	41,0101 М	0645494617	1371511371	0.7/4.144/
azwin	Z11WHW1	0,1Л)ШЛ	L ЗВ 1Л155	0,15-161.1771	■ l,iiooi*oe	0,7100915

Рис. 3. Вектор Т случайной величины, распределение которой близко к нормальному

Так же необходимо рассчитать матрицу А (рис. 4).

teerpw^i А 1			1	4		6 У
1	О-ОЫОв"	с осоос	0О0ООС-	ClQOOOO	0.0000»	C00OOD	0.OODOD
2	-1.09971	МЗЖ2	Охта»	0.00000		сооопо	0.00000
S	<102135	■:.ойбс>	0.42391	0.00000	0,00000	С 00000	оосоос
4	6,00461!	0,01915	-0,04505-	0.20415-	оооооо		0.00000
5	L11644	01)054	0.04406	4101440	-0,47025
6	00601/	02)03601	О.ООЖ»	Aoaus-	002197	(L0J061	0^0000
У	0 009^7	АШ7И	0.0UM	ОиШЖ!	O.CHUC	0.00146	амяа

Рис. 4. Матрица преобразования

Теперь есть все данные, необходимые для моделирования новых значений с учетом вектора средних и ковариационной матрицы (рис. 5).

смоделированные значения
pH	аммиак	нитриты	фосфаты	железо	медь	нефтепроду
7,764077061	69,63069	0,223294	0,8278838	0,680131	0,0320497	0,4374978
7,881163463	92,34819	0,026275	0,7339362	2,0109141	0,0307658	0,2051637
7,851039645	114,2831	0,732872	1,1864087	1,1470297	0,0440688	0,0604161
7,803661249	64,84405	0,321486	1,0559895	0,2088294	0,0512114	0,3802101
7,987906313	52,98347	0,87609	0,5700028	3,0453575	0,0222696	0,0208099
7,796309884	131,4354	0,362405	0,9214862	0,7621463	0,0136732	0,2060312
7,85083789	56,25079	0,11002	1,089813	2,8433403	0,0176159	0,1240987
7,873638423	100,1104	0,203225	1,062166	1,3074708	0,0736371	0,2064887
7,833361459	90,31652	0,371347	0,6652116	2,2070665	0,0141964	0,606874
7,756163609	52,80175	0,734947	1,0131565	0,5732404	0,0270907	0,390778
7,866105593	155,654	0,134656	1,260059	2,4293045	0,0202632	0,1370673
7,782977798	16,43259	0,28411	1,0628007	0,5012019	0,009696	0,4566754

Рис. 5. Смоделированные значения по 7 показателям качества сточных вод при производстве печатных плат

Для проверки правильности смоделированных значений, рассчитаем вектор средних (рис. 6) и сравним его с вектором средних исходных данных (рис. 1). Видим, что значения среднего для каждого показателя достаточно близко к истинному.

средние I 7,844896153 73,34393 0,47753 0,90589Б7| 1,7956183 0,0317889 0,2888539

Рис. 6. Вектор средних для смоделированных данных

Для машинного обучения необходимо самостоятельно сгенерировать столбец Y, который определяет исправность (Y=1) или (Y=0) неисправность системы. Если хотя бы один из показателей приближается к своему предельно допустимому значению концентрации, то система считается неисправной.

Далее проведем предобработку данных с помощью методов машинного обучения, реализованных в разработанной программе на языке Python.

Г №«w»w

			ч
i	^<Л	rtx	же	ЬЖ1	1 ж	ие		1»
Г	и	МВ	Ж4	aw	вл	ТЖ*	ахя<	ап
.1!	и	fN	•	am	1М	ат	ажж	и¹
	и	TS	Н5	ам	ал	11	wre	ам
	ы		• I	LW
*	1*	гл	ем	14В		аж	1Я6Ж
7	и			а*	1.1	1В	АРП	U1
1	14		гл	ат		ip		им
*		741 МУ	774	ат	LT	иг	аги	343
T9		741 МУ	■и	здз	11		алп

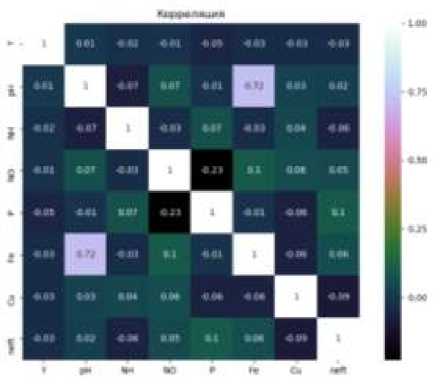
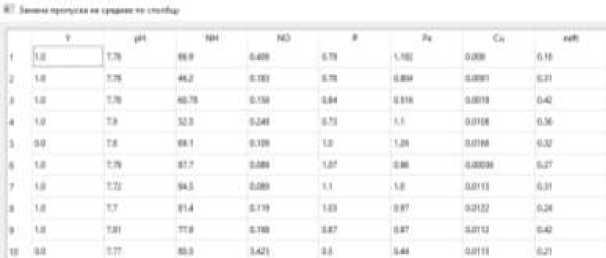
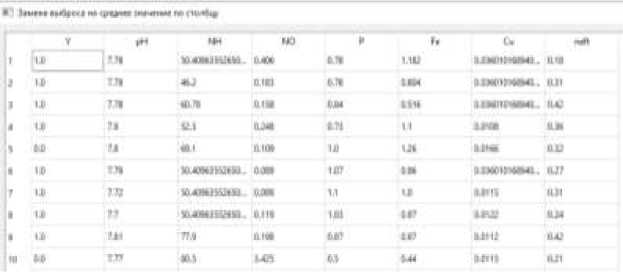
Рис. 7. Считывание данных

Первым этапом предварительного анализа данных является вычисление численных характеристик показателей качества – математическое ожидание, дисперсия, ско (рис. 8).

: .w* • ипмслт. umnwt wenrtwt ажчжмым irrhirww ммаммжж 1лмшеж i rw w «I*. i mwn* tufXjwin. гиимм* меиеша. nemuw. идолы tcj—nn-

nx "wewesx- «м»*ыше1 r« i—гт’чм сгштж iwwi амгчжмш- e ^ 'w«»tn жеяыпмям с —пчтлэ irotTinM 'urinna ■ —!?>—?ж utmnM’V r nx •wewev't* жпеав". tmwnm iiit'MiL цашчшв ваигаят. иехижж е wm,w ш * «vrw. s мп V и Mi и

Рис. 8. Подсчет числовых характеристик

По вычисленным значениям стандартного отклонения можно отметить, что третий и пятый показатели качества сточных вод имеют очень большой разброс значений, относительно их средних.

Далее необходимо определить коррелированность показателей между собой и коррелированность каждого из показателей с откликом. В реализованной программе таблица корреляций отображается с помощью цветовой схемы (рис. 9), где чем темнее цвет, тем меньше корреляция между значениями.

Рис. 9. Расчет корреляционной матрицы

Данные на производстве часто содержат пропуски и выбросы, связанные с неисправностями техники, ошибками оператора и другими причинами. В связи с этим, необходимо избавиться от пропусков и выбросов. Первым способом удаления пропусков является удаление строки, содержащей пропуск хотя бы в одном показателе. Однако данный способ может удалить данные, являющиеся важными для дальнейшего исследования. Второй способ - замена пропуска на соседнее по столбцу значение. Минус этого способа в том, что он может увеличить количество выбросов в данных. Последний способ, исследуемый в данной работе, -замена пропуска на среднее значение данного показателя (рис. 10). Данный способ является наиболее оптимальным среди всех, т.к. не оказывает влияния на другие показатели качества и не увеличивает количество выбросов в текущем показателе.

Для обработки выбросов так же возможно применение всех трех способов. На рис. 11 представлена замена выброса на среднее значение.

Рис. 10. Замена пропусков на среднее значение показателя

Рис. 11. Замена выброса на среднее по показателю

Далее необходимо нормализовать данные и перейти к главным компонентам. По нормализованным данным строим главные компоненты и график каменистой осыпи, с помощью которого определим, сколько компонент необходимо использовать (рис. 12-13).

Рис. 12. График каменистой осыпи

• Парашда пивным юыпсмжнгвм

। г э < 1 б ? ।

J 1Л -006781703747.. 0Л1 Л17В738О6_ 0515315477706- 0X4957^115.. О0013ЮС3176- 0 30016219721- 6JS604X4W-.

4 1.0 -0 0157139670». -051122657881. 0 004«147695 -0X34*115*17.. -МОТ1561П. -МО ЮТЫ». -0 000508996»

) ПО -007855 791064- -03X670547881- 001»7Ы66в4«_. -НШ5в67В114Б_. OJ0G4 5O58S221L. -000015472757... -ODXG4488Ha_.

i то Ч1мгд8эгт_ чюимпзбХ. олшв74Г1е«. -аштзмзг*.. олертмгот.. осгозатвок»- -оам^итм..

7 10 -0М1175 7В7Я- -ЛЛГ$ЗМв?4_ 0М114Пи^44. -ОаПЦТТщЧ- OjaK^VtiH.. ПДЖ$5 5Г¥74-. -OOGC6164№_.

I 1Л -0М379119ЮЗ. П4НЗв5Ы1812_ 0003712160193- -00X51773241 - 0^011393X14- О«1633й64171„ ОХИЧИТВ-

5 U -0 0*746114». -CJX56I7DO0C. Ой261йй1Ли aOXiB^OUS. C-XCW50M* -ОЮ17®66601. -0 0003*610680.,

10 ПО ODH197356H- О01П»153142_ 0031893609543- 0033071817940- 0X0447132129- й«П$963С5Г_ 000025607597-

Рис. 13. Переход к главным компонентам

Список литературы Задача моделирования коррелированных многомерных данных

Алексеева В.А. Использование методов машинного обучения в задачах бинарной классификации / В.А. Алексеева. - Automation of control Processes № 3 (41) 2015 С. 58-63
Биргер, И. А. Техническая диагностика / И. А. Биргер - М.: Машиностроение, 1978. - 240 с.
Жуков, Д.А. Задачи обеспечения эффективности машинного обучения при диагностике технических объектов / Д.А.Жуков, В.Н.Клячкин // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. - 2016. - № 1 (10). - С. 172-174.
Клячкин, В.Н. Применение методов машинного обучения при решении задач технической диагностики / В.Н.Клячкин, И.Н. Карпунина, Ю.Е.Кувайскова, А.С.Хорева // Научный вестник УВАУ ГА(И). - 2016. - Т. 8. - С. 158-161.
Кувайскова, Ю.Е. Прогнозирование состояния источника водоснабжения в целях обеспечения качества воды / Ю.Е. Кувайскова, Е.М. Булыжев, В.Н. Клячкин, Д.С. Бубырь // Справочник. Инженерный журнал с приложением. - 2016. - №5. - С.37-42

Статья научная