Задача о центральной продольной трещине нормального отрыва с наполнителем в полосе

Рассматривается задача о напряженно-деформированном состоянии полосы, содержащей прямолинейную трещину, параллельную границам полосы. В литературе рассматриваются два типа задач о продольных трещинах в полосе. К первому типу можно отнести задачи о трещине в полосе, границы которой свободны от напряжений, а к берегам трещины приложены нагрузки [1–7]. Ко второму – задачи о трещинах со свободными берегами с различными видами условий на границах полосы [1]. В вышеуказанных работах рассматриваются трещины типа разрезов, однако на практике трещины могут возникать в результате непроклейки слоистых элементов конструкций. Дефекты такого вида можно считать заполненными неким клейким веществом [8]. В данной статье рассматривается задача о центральной продольной трещине с наполнителем в полосе. В рамках этой модели предполагается, что скачки вертикальных перемещений на берегах трещины пропорциональны нормальным напряжениям на ее берегах [8].

Рассмотрим упругую полосу толщины 2h . Материал полосы будем характеризовать двумя упругими характеристиками: модулем сдвига ц и коэффициентом Пуассона v . Нижняя граница полосы жестко заделана, а к верхней границе приложена нормальная сосредо-ченная нагрузка. Введем две локальные декартовые системы координат Oixzi (i = 1,2) так, как показано на рис. 1.

На серединной плоскости полосы при z1 = h (z2 = 0), имеется продольная трещина с наполнителем, занимающая область x е(-a; a). Напряжения и перемещения, которые относятся к верхней половине полосы (x е (-~; +~), 0 < z1 < h ), будем обозначать нижним ин дексом 1, а к нижней (x е (-^; +то), 0 < z2 < h ) - 2.

Граничные условия:

^ _z 1 ( x ,0 ) = Q S ( x ) , T _xz 1 ( x ,0 ) = 0, u ₂ ( x , h ) = 0, w ₂ ( x , h ) = 0.                    (1)

Условия на серединной плоскости полосы:

Oz2 (x,0) = Oz 1 (x, h) , Txz2 (x,0) = Txz 1 (x, h) , u2 (x,0) = u1 (x, h), w2 (x,0) - w1 (x, h) =

A (x), |x| < a, 0,      |x| > a,

o z i ( x , h ) = cf ( x ) , | x | <  a ,

где A(x) = 4a2 -x2 f (x), f (x)e C2a a], f (±a)^ 0, c - коэффициент, который характеризует наполнитель.

Требуется определить скачок вертикальных перемещений на берегах трещины и коэффициенты интенсивности напряжений (КИН).

- xk   -   4   - a  A Q   г h      M- c

Введем безразмерные величины xk = —, zk = —, a = —, Q =—, h = —, Ц =—, k l     k   l l       lE       l        EE

ɶ

u

ɶ

w

ɶ

Tzk xz k

u =, w = —, Т к =---, l l xzk E

Ozk       , „                                         i ozk =---, где l, E - характерные величины ([l] = м, [E] = Па). В zE

дальнейшем тильды над функциями и переменными будем опускать, считая, что все преобразования выполняются над безразмерными величинами.

Метод решения

Для решения задачи воспользуемся интегральным преобразованием Фурье:

^^

f ( fl ) = J f ( x ) e ^s’ dx , f ( x ) = J f ( fl ) e- Sxd ^ .

2 n

^^

В пространстве трансформант компоненты напряженно-деформированного состояния полосы могут быть представлены в виде линейных комбинаций вспомогательных функций, которые связаны с напряжениями и перемещениями точек ее верхней границы такими формулами [9]:

« = oz (fl,0), e = MW(fl,0), Y=MS(fl,0), 5 = — i^fxz (fl,0),(4)

p где S = — iflu (fl, z), W = pw (fl, z), p =|fl|.

Трансформанты напряжений и перемещений полосы имеют вид [9]:

2 ц W ( fl , z ) = ( ( 2 — to ) sh pz — to pz ch pz ) a + 2 ( — to pz sh pz + ch pz ) в +

+2((1 — to)shpz — topzchpz)y — topzshpz5,(5)

2 ц S ( fl , z ) = to pz sh pz a + 2 ( ( 1 — to ) sh pz + to pz ch pz ) в +

+2 (to pz sh pz + ch pz) y +((2 — to) sh pz + to pz ch pz )5,(6)

o z ( fl , z ) = ( ch pz — to pz sh pz ) a + 2 to ( sh pz — pz ch pz ) в — 2 to pz sh pz y —

—((1 — to) sh pz + to pz ch pz )5,(7)

— —^_xz ( fl , z ) = ( — ( 1 — to ) sh pz + to pz ch pz) a + 2 to pz sh pz e +

+2to(sh pz + pz ch pz )y +(ch pz + to pz sh pz )5.(8)

Запишем условия (1)–(2), с учетом формул (4), в пространстве трансформант Фурье:

« 1 = Q , 5 1 = 0, « 2 = o z 1 ( fl , h ) , 5 2 = — ^{i fl}- T z _z 1 ( fl , h ) ,

p

Y2 = MS1 (fl,h), в2 — MW1 (fl,h) = MpM(fl), S2(fl,h) = 0, W2(fl,h) = 0, где M (fl)= jA(t)efldt.

— a

Антоненко Н.Н.                                Задача о центральной продольной трещине нормального отрыва с наполнителем в полосе

Используя формулы (5)-(8), из последних соотношений найдем Д , Y , а ₂, в ₂, / 2 , 5 2 .

Трансформанты нормальных напряжений в точках срединной плоскости полосы oz 1 (^, h) при- мут такой вид:

Oz 1 (^ h) =

PA1 (P)M(£)-QA2 (P) D(P)

где A 1 ( p ) =- иоД a 1 + a 2 e ^{2 P 1} + a 3 e ^{4 P 1} + a 4 e ^{6 P 1} - a 1 e ^{8 P 1} ) ,

A₂ ( p ) = b 1 e ^{- P 1} + b 2 e -3 ^{P 1} + b 3 e ^{- 5P 1} + b 4 e ^{- 1 P 1} , D ( p ) = a 1 + k e ^- 4 ^{P 1} + a 1 e -8 ^{P 1} , a 1 = 6 ² - 2 6 , a ₂ = 2 6 ( - 6 + 2 6 p 1 + 2 6 p 2 ) , a 3 = 8 p 1 ( 6 + 6 ² + 2 6 2 p 1 ² ) , a 4 = 2 6 ( 6 + 2 6 p 1 - 2 6 p 1 ² ) , b = - a 1 ( 1 + P 1 ) , b 2 = 2 6 + to + 3 6 P 1 + 4 6 P 1 , Ь з = 2 6 + to - 3 6 P 1 + 4 6 P 1 , b 4 = - a 1 ( 1 - P 1 ) , 6 = 0,5/ ( ( 1 - v ) ) , p 1 = ph , 6 = 1 - 6 , k = - 2 ( 2 + a 1 + 8 ® ² p 1 ² ) .

Используя связь между оригиналами и трансформантами нормальных напряжений (9) в точках срединной плоскости полосы и последнее из условий (2), получим интегральное уравнение задачи:

a

ncf (x)= j A(t)K(t-x)dt-QL(x),

- a x 7 PA1 (P)      Я \ 7 A2 (P)      Я где K (z) = —-——cospzdp, L(z) = —-—-cospzdp .

0 D (P)                  0 D (P)

Выделим в ядре интегрального уравнения регулярную K 1 ( z ) и сингулярную K ₂ ( z ) части:

a

a

ncf (x )= j A (t)K1 (t - x) dt - Ц6 j A (t) K 2 (t - x) dt - QL (x),

7 где K ₁ ( z ) = j P

- a

ОД + ^6 ] cos

- a

7                  A1 ( P )

pzdp , K ₂ ( z ) = I p cos pzdp , lim —-—- = - p.6.

0            P ^⁷ D ( P )

Интеграл K ₂ ( z ) расходится, поэтому его будем понимать в следующем смысле:

+7                   +7                            2   2

K ₂ ( z ) = [ p cos pzdp = lim [ p cos pze q^P dp = lim —--- z-^-

0               q ^ ^{0 + o} 0                     q ( q ² + z ² ) ²

1 z 2 .

a a (t) ,

Поскольку ----- -dt при x = t имеет неинтегрируемую особенность, то воспользуемся фор-

- a ( t - x ) 2

мальным равенством:

— J

A (t) t - x

a

a

+j

d (A (t))

a

- a

-

a

t

-

x

=j

-

a

A ‘ ( t ) dt

t

-

x

Математическое обоснование (11) приведено в [10]. В (11) использован тот факт, что берега трещины должны смыкаться, т.е. A ( ± a ) = 0.

Окончательно интегральное уравнение задачи (10) принимает вид:

aa

ncf (x)= j ya2 -12 f (t)R(t-x)dt + Ц6 j

- a                                   - a

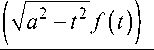
t - x

dt - QL ( x ) .

Неизвестную функцию f ( x ) будем искать в виде:

n f (x) = ^«U21 (x), i=0

где U 2 i ( x ) - полиномы Чебышева второго рода.

Для определения неизвестных ai раскладываем левую и правую части уравнения (12) в линейные комбинации полиномов Чебышева и приравниваем коэффициенты при полиномах одинакового порядка. Количество членов в линейных комбинациях выбираем из условия, чтобы решения, полученные на n -м и n + 1-м шагах, отличались на некоторую наперед заданную величи- ну.

‘

а (V a 2 -12f (t))

Используя асимптотические оценки, полученные в [8], для интеграла                   dt ,

J t - x

- a получаем цaf (a) 42a az 1 (x, h) =-------p--+ O (1), r = x - a, при x ^ a + 0.

2 r

Формула для вычисления коэффициентов интенсивности напряжений принимает вид:

K 1 = ^af (a)^na , где функция f (x) вычислена по формуле (13).

Численные расчеты проведены для трещины длины 2 a = 2 . Полоса находится под действием нормальной сосредоточенной силы Q = 1. Ниже в табл. 1-4 приведены результаты, которые иллюстрируют зависимость КИНов от упругих характеристик полосы, ее полуширины и наполнителя трещины.

Таблица 1

Зависимость коэффициентов интенсивности напряжения от толщины полосы ( v = 0,3 , ц = 1 )

ha	2	3	4	5	10	100
-K= , c = 1 Q V а a	0,11205	0,08416	0,06611	0,05408	0,02788	0,00282
-I4= , c = 0 Q n aa	0,30996	0,21577	0.16476	0,13299	0,06733	0,00676

Таблица 2

Зависимость коэффициентов интенсивности напряжения от модуля сдвига полосы ( v = 0,3 , ha = 10 )

Ц	1	2	3	4	5	10
~^=, c = 1 Q V a a	0,02788	0,03945	0,04577	0,04976	0,05250	0.05890
-I4= , c = 0 Q n aa	0,06733	0,06733	0,06733	0,06733	0,06733	0,06733

Таблица 3

Зависимость коэффициентов интенсивности напряжения от коэффициента Пуассона полосы ( ц = 1 , ha = 10 )

v	0,1	0,2	0,3
K I— , c = 1 Q V a a	0,02375	0,02563	0,02788
KIM= , c = 0 Q y a a	0,06697	0,06709	0,06733

Антоненко Н.Н.

Задача о центральной продольной трещине нормального отрыва с наполнителем в полосе

Таблица 4

Зависимость коэффициентов интенсивности напряжения от коэффициента, который характеризует наполнитель c ( v = 0,3 , ц = 1 , ha = 10 )

c	1	2	3	4	5	10
K I	0,02788	0,01757	0,01282	0,01009	0,00832	0,00443
Q П аа

Из табл. 1–4 можно сделать выводы:

• 1)    увеличение полуширины полосы и коэффициента c приводит к уменьшению КИНов;

• 2)    к увеличению КИНов приводят увеличение модуля сдвига и коэффициента Пуассона полосы;

• 3)    для случая трещины, берега которой свободны от напряжений ( c = 0), упругие характеристики полосы практически не влияют на КИНы.

• 1.    Murakami, Y. Stress intensity factors handbook: in 2 Vol. / Y. Murakami. – Pergamon Press, 1987. – Vol. 1. – 1566 p.

• 2.    Сметанин, Б.И. Некоторые задачи о щелях в упругом клине и слое / Б.И. Сметанин // Инж. ж. МТТ. – 1968. – № 2. – С. 115–122.

• 3.    Саврук, М. П. Двумерные задачи упругости для тел с трещинами / М.П. Саврук. – Киев: Наук. думка, 1981. – 324 с.

• 4.    Александров, В.М. Продольная трещина в преднапряженном тонком упругом слое со свободными границами / В.М. Александров, Б.И. Сметанин // ПММ. – 2005. – Т. 69, Вып. 1. – С. 150–159.

• 5.    Fichter, W.B. Stresses at the tip of a longitudinal crack in a plate strip / W.B. Fichter. – Washington: National Aeronautics and Space Administration, 1967. – 55 p.

• 6.    Александров, В.М. Продольная трещина в ортотропной упругой полосе со свободными гранями / В.М. Александров // Изв. РАН. МТТ. – 2006. – № 1. – С. 115–124.

• 7.    Пожарский, Д.А. Асимптотические решения смешанных задач для упругой полосы и клина / Д.А. Пожарский, А.А. Молчанов. – Вестник Донского государственного технического университета. – 2010. – Т. 10. – С. 447–454.

• 8.    Антоненко, Н.М. Моделювання тріщини нормального відриву з наповнювачем на межі багатошарового пакета та півплощини / Н.М. Антоненко, І.Г. Величко // Прикл. проблеми мех. і мат. – 2011. – Вип. 9. – С. 141–149.

• 9.    Ткаченко І.Г. Двомірна мішана задача термопружності для багатошарової основи / І.Г. Ткаченко // Прикладні проблеми механіки і математики. – 2005. – Вип. 3. – С. 70–78.

• 10.    Лифанов, И.К. Метод сингулярных интегральных уравнений и численный эксперимент (в математической физике, аэродинамике, теории упругости и дифракции волн) / И.К. Лифанов. – М.: Янус, 1995. – 520 с.