Задача о поиске оптимального количества стран на ограниченной территории

DOI:

Предположим, что мир состоит из двух континентов.

Нами рассматривается долгосрочный период – может включать в себя сотни, тысячи лет, или любой промежуток времени, в течение которого происходит изменение границ государств, разделение государств. Все курсы валют 1 : 1. Цены на товары везде одинаковые, как на внутренних рынках, так и на внешних, так как все государства мира находятся в ВТО. В силу этого цены на товары в различных валютах принимают одно и то же значение.

Пусть существует некий абстрактный континент со своей площадью территории L . На континенте производится некий абстрактный продукт (перечень каких-то жизненно необходимых товаров). Континент разделен на несколько государств со своими площадями их территорий S ⁱ , i = 1,..., n .

S ¹ + 5 ² +.... + S n = L S i >  0 i = 1, 2,..., n , n + const.                       (1)

Количество государств может меняться с течением времени.

В каждом государстве размещается «компрадорская» управляющая структура. Каждая структура самостоятельна и не подчиняется государству. Ее официальная функция – эмиссия национальной валюты государства [2], то есть сколько государств на континенте – столько и национальных валют – столько же «компрадорских» управляющих структур. Теневая функция «компрадорских» управляющих структур – ежегодно изымать из континента определенное количество ежегодно производимого абстрактного продукта. Реализация этой теневой функции излагается далее.

У компрадорских структур есть «хозяин», живущий на другом континенте. Он производит свой абстрактный продукт только для себя (в особенности авианосцы с бомбардировщиками), и никому его не продает, так как является «мировым паразитом», который потребляет больше, чем производит.

«Хозяин» ежегодно может печатать неограниченное количество своей валюты и скупать за нее абстрактный продукт, ежегодно производимый государствами «бедного» континента.

«Компрадорские» структуры в каждом государстве «бедного» континента ежегодно печатают ровно столько национальной валюты, сколько государство получило валюты «хозяина» в обмен на часть своего ежегодного абстрактного продукта (напоминаем, что все курсы валют 1 : 1). Эта валюта «хозяина» более уже не используется государством, направляется в золотовалютные резервы «компрадорской» структуры и из золотовалютных резервов отдается назад «хозяину» в обмен на казначейские векселя «хозяина» [5], платить по которым он никогда не будет, по той причине, что у него есть авианосцы с бомбардировщиками.

Национальная валюта каждому государству нужна для реализации оставшегося ежегодного абстрактного продукта внутри государства между его членами – реализация функции денег – средство обращения [3]. Напоминаем, что внутренние цены диктуются ВТО и равны внешним ценам, а также все курсы валют 1 : 1, так что для реализации оставшегося абстрактного продукта внутри отдельно взятого государства этому государству необходим объем национальной валюты, равный полученному объему валюты «хозяина». Проще говоря, для каждого государства важно, чтобы объем проданного продукта равнялся объему оставшегося.

Ежегодная доля абстрактного продукта, которая продается хозяину, зависит от площади территории государства, и с ростом площади эта доля уменьшается, так как «компрадорской» управляющей структуре и ее «хозяину» становится сложнее контролировать территорию с большей площадью и соответственно большей численностью населения, которое время от времени бунтует [6], что и затрудняет изъятие абстрактного продукта из государства. Обозначим эту долю за P_i ( Sⁱ ) . Она принимает значения из отрезка [0, 1].

Итак, по условию:

P_t ( S i ) e [0,1] , dPS! <  o , s i _{e (}o, l ] , i = 1, 2,..., n.           (2)

Не забываем, что n ≠ const.

Кроме того, на континенте действует экономическое правило роста эффективности производства абстрактного продукта каждого отдельно взятого государства с ростом площади терри- тории этого государства (эффект от масштаба производства [3]). Особенно этот эффект, в нашем случае от роста площади территории, ярко выражается, например, в аграрных государствах, ориентированных на производство сельскохозяйственной продукции, а также в государствах, ориентированных на добычу полезных ископаемых. Обозначим эту взаимосвязь коэффи-циентомKi(Si), зависящим от площади государства.

Итак, по условию:

K(S^ >  0 , dKdSSp- >  0 , S i e (0, L ] , i = 1, 2,..., n.            (3)

Условие появления государств: мы предполагаем, что при образовании на континенте нового n + 1 государства выполняется условие:

K n _{+ 1}( S^{n + 1}) = K i (S i ) и P n _{+ 1}( S^{n + 1}) = P ( S i ) при S n ^{+ 1} = S i для какого-то i e {1,2,..., n} .

Условие слияния государств: мы предполагаем, что при слиянии каких-то государств выполняется условие: новые функции P и K для нового государства, получившегося из нескольких государств, принимаются равными функциям P i и K i какого-то i -го государства, участвовавшего в слиянии.

Объем производства абстрактного продукта в каждом государстве определяется равенством:

S i e (0, L ] i = 1, 2,..., n.                                         (4)

,

При этом ясно, что с ростом площадей всех государств, какие-то государства вливаются в другие, так как L = const, и в одном государстве не может быть несколько национальных валют, и соответственно «компрадорская» управляющая структура тоже остается только одна.

Ежегодный объем абстрактного продукта, который отдается «хозяину», определяется выражением:

S i - K i (S^l) - P ( S i ) S i e (0, L ] i = 1, 2,..., n.                        (5)

,

Ежегодный объем абстрактного продукта, который остается в каждом государстве, определяется выражением:

S i - K ( S i ) • (1- P ( S i )) S i e (0, L ] i = 1, 2,..., n.                  (6)

,

С точки зрения «компрадорских» структур и их «хозяина» для ежегодного извлечения из континента максимально возможного объема абстрактного продукта необходимо найти максимум следующего функционала:

n

G ( S 1 , S ²,..., S n ) = ^ S i - K i ( S i ) - P ( S i ) l = 1

S ¹ + S ² +...+ Sⁿ = L = const                                        (7)

n ^ const.

Если n = const, то этот функционал есть функция от n переменных, и максимум ищется за счет взаимного изменения границ между государствами без их исчезновения. В этом случае задача сводится к поиску условных экстремумов на поверхности:

S ¹+ S ²+ + Sⁿ = L 0< S < L = 1, 2, ..., n. ^,

Поиск максимума для функционала (7) сводится к максимизации выгоды (сравнение предельных выгод и предельных издержек от изменения площадей государств) [3]. Все сводится к непрерывному попарному сравнению приращений (S^ - Ki (S^ ) • Pi (S^ )) ASi для l-х государств, где ∆Si есть изменение площади i-го государства. Приращение (Sξi ⋅Ki(Sξi ) ⋅Pi(Sξi )) ∆Si определяется по теореме Лагранжа о среднем приращении [1]. До тех пор, пока производная (Si ⋅ Ki(Si) ⋅ Pi(Si))' положительна, «хозяину» «компрадорских» структур будет выгодно увеличивать площадь i-го государства за счет территории других государств с меньшим значением производных. Если же производная отрицательна, то выгодно уменьшать площадь государства, либо увеличивая площади государств с положительными производными либо создавая новые государства по условию, обозначенному выше, и продолжая оперировать уже и с их территорией.

На рисунке 1 показан один из возможных сценариев процесса максимизации функционала (7) для каких-то i -го и j -го государств, где i ≠ j . Площадь фигуры ABCD есть приращение ежегодного продукта для «хозяина» в i -м государстве за счет изменения площади i -го государства на ∆ S ⁱ , ∆ Sⁱ >  0 . Площадь фигуры EFGH есть приращение ежегодного продукта для «хозяина» в j -м государстве за счет изменения его площади на ∆ S ^j , ∆ S ^j <  0 . Для сохранения равенства (1) предполагается, что ∆ Sⁱ = -∆ S^j .

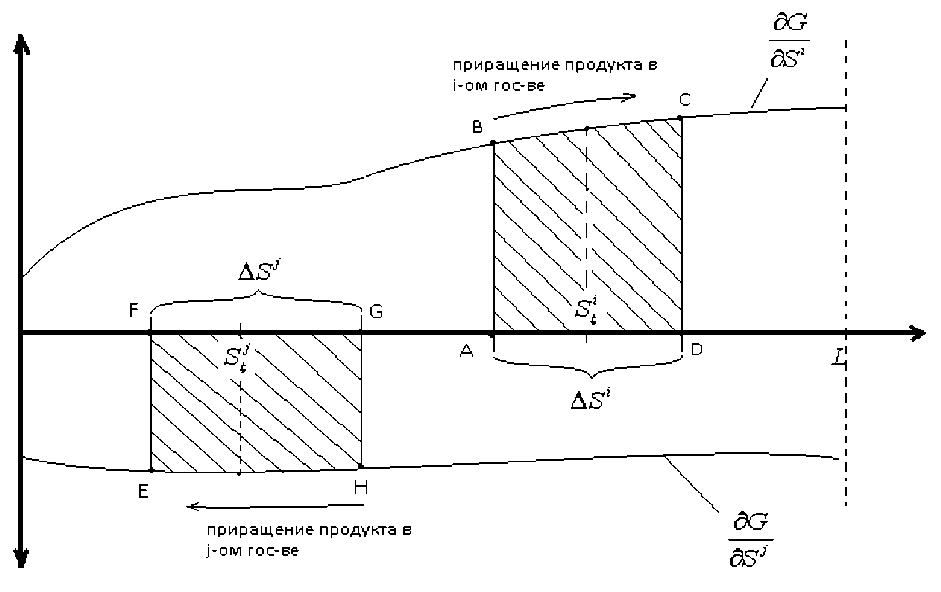
Рис. 1. Приращение продукта для «хозяина» за счет увеличения площади в i-м государстве и за счет снижения площади в j-м государстве

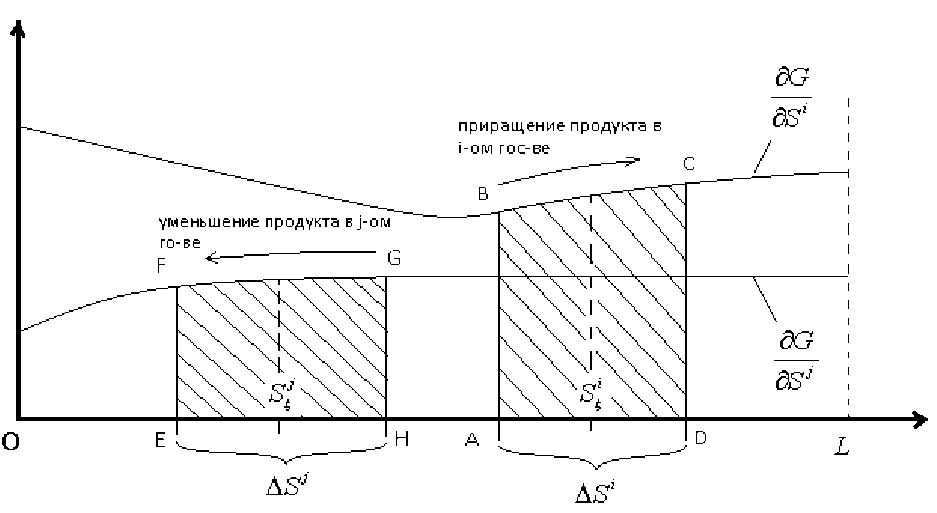
Рис. 2. Приращение продукта для «хозяина» за счет увеличения площади в i -м государстве и уменьшение продукта для «хозяина» за счет снижения площади в j -м государстве

На рисунке 2 показан еще один сценарий процесса максимизации для каких-то i -го и j -го государств, i * j . Здесь площадь фигуры ABCD есть также приращение ежегодного продукта для «хозяина» в i -м государстве за счет изменения площади i -го государства на A S‘ , A S i >  0 . Площадь фигуры EFGH есть теперь уменьшение ежегодного продукта для «хозяина» в j -м государстве за счет изменения площади j -го государства на A S j , A S^j<  0 . Для сохранения равенства (1) опять предполагается, что A S i = -A S^j . Подобное изменение площадей государств «хозяину» будет выгодно, если площадь фигуры ABCD будет больше площади фигуры EFGH или ( s ; • K i ( S - ) • P i ( S - )) ' A S i >  ( S / • K j ( S / ) • P j ( S ^T )' ( -A S^j ).

Приведем тривиальный пример для системы (7).

Пример 1. Пусть изначально на континенте было только одно государство.

Тогда по условию появления государств функции P i и K i равны во всех государствах «бедного» континента. Обозначим их за P и K . Пусть площади всех государств континента также всегда равны. Обозначим их соответственно за S .

Пусть P и K линейные функции

P(S) = a 1 • S — a 1 • L a1 = const < 0 S e(0, L]

K (S) = a2 • S a2 = const > 0 S g(0, L]

Тогда

G (S1, S2,..., S”) = G (S) = n • S • P (S) • K (S) = L • P (S) • K (S).

L

Приравниваем производную к нулю и получаем, что S = —.

То есть в этом случае «хозяину» выгодно делить континент на два государства.

Максимизация функционала (7) может оказаться невыгодной для «компрадорских» структур и их «хозяина» в том смысле, что если в первый год изъять из континента слишком много продукта (или несколько лет изымать продукт по максимуму), то во второй год (следующие года) больше некому будет снова производить этот продукт (из-за вымирания населения континента [4]).

Поэтому оптимальным для «хозяина» будет вариант, когда и население не слишком быстро вымирает, и соответственно продукт можно изымать очень долго. Лучше дольше, но больше, чем сразу, но меньше.

С точки зрения каждого отдельно взятого государства «бедного» континента для реализации внутреннего ежегодно остающегося продукта внутри государства (реализация функции денег – средство обращения) необходимо, чтобы для каждого государства объем его ежегодно отдаваемого продукта равнялся объему остающегося. Это также устраивает и «хозяина» ввиду вышесказанного. Для этого необходимо решить систему:

S1 • K i( S 1) • P1( S 1) = S1 • K i( S 1) • (1 - P1( S 1))

S2 • K2(S2)• P2 (S2) = S2 • K2(S2)• (1 -P2 (S2))

..................................... (8)

S" • K„ (S”) • P (S” ) = S” • K„ (S”) • (1 - P (S”))

S1 + S2 +... + S" = L = const

" * const.

Из этой системы следует система

S1 • K1(S 1)• P1(S 1) + S2 • K2(S2)• P2(S2) + ...+

+S" • K" (S") • P" (S" ) = S1 • K 1(S 1)x(1 - P1(S 1)) +

+S2 • K2(S2)x(1 -P2(S2)) + ... + S" • K"(S")• (1 -P"(S"))                      (9)

S1+S2+...+Sn =L=const

" * const.

Но из системы (9) уже не следует система (8). Системы могут оказаться неразрешимыми с математической точки зрения, но обязательно разрешимы при приближенном подборе площадей для приближенного выполнения равенств. Ежегодные объемы производств, вычисленные отдельно по каждой системе, могут оказаться разными. Если все государства «бедного» континента вычисляют свои площади по системе (9), то в государствах могут возникнуть дисбалансы между объемом национальной валюты и оставшимся абстрактным продуктом, причем эти дисбалансы в отдельно взятых государствах образуют баланс на всем континенте. Дисбалансы в каждом государстве в этом случае решаются торговлей между этими государствами.

Пример 2. В условиях примера 1 системы (8) и (9) равносильны друг другу. И все сводится к равенству:

K (S) • P (S ) = K (S) • (1 - P (S)).

1 2La+1

.

Решаем его относительно S , и получаем, что S =---¹---

2     a1

0.51         L

Если, например, а 1 = ——, то S = —. То есть 51 государство.

Если же государства «бедного» континента решили обеспечить свое максимальное благополучие, то им необходимо максимизировать функционал:

F ( S ¹, S ²,..., Sⁿ )= ∑ ⁿ Sⁱ ⋅ K_i ( Sⁱ )×(1 - P_i ( Sⁱ ))

i = 1

S ¹ + S ² + ... + Sⁿ = L = const                                 (10)

n ≠ const.

Процесс максимизации этого функционала аналогичен процессу максимизации функционала G ( S ¹, S ²,..., Sⁿ ) , но с одним отличием – производные всех слагаемых функционала F ( S ¹, S ²,..., Sⁿ ) положительны.

Пример 3. Пусть изначально на континенте было только одно государство, которое с течением времени было разделено на несколько.

Тогда по условию появления государств функции P i и K i равны во всех государствах «бедного» континента. Обозначим их за P и K . Пусть площади всех государств континента также всегда равны. Обозначим их соответственно за S . Получим:

F ( S ¹, S ²,..., Sⁿ )= F ( S )= n ⋅ S ⋅ (1 - P ( S )) ⋅ K ( S )= L ⋅ (1 - P ( S )) ⋅ K ( S ).

Так как это возрастающая функция, то она достигает своего наибольшего значения тогда, когда S = L . То есть для государств континента в этом случае наиболее выгодно объединиться обратно в одно государство.

Пример 4. Если в условиях примера 3 предположить, что площади государств могут быть различными, то функционал (10) будет выглядеть следующим образом: n

F(S1,S2,...,Sn)=∑Si⋅K(Si)⋅(1-P(Si)), n ≠ const, i=1

S1+S2+....+Sn =L=const.

Если еще предположить, что вторая производная ( Sⁱ ⋅ K ( Sⁱ ) ⋅ (1 - P ( Sⁱ ))) '' положительна на всем полуинтервале (0, L ] , то максимум функционала также будет достигаться тогда, когда государства континента объединятся в одно государство.

Из примера 4 следует теорема.

_∂ 2 _F

Теорема 1. Если все вторые частные производные i 2 функционала (10) положи тельны, то максимум этого функционала достигается тогда, когда все государства континента объединятся в одно государство.