Задача о распространении акустических волн в пористой среде, насыщенной пузырьковой жидкостью

Исследование процессов распространения волн давления в насыщенных пористых средах связано не только с решением практических задач сейсмики, защиты объектов, неразрушающего контроля и т. д., но и с пониманием фундаментальных основ волновых процессов в таких средах.

Отметим работы посвященные исследованию динамики волн давления в насыщенной пузырьковой жидкостью пористой среде.

В ряде работ В.Е. Донцова [1–3] на установке «ударная труба» экспериментально изучена эволюция и структура волн давления в пористой среде, насыщенной жидкостью с пузырьками газа. Насыщающей жидкостью была вода, газом – воздух или углекислый газ. В качестве рабочей среды использовалась хаотическая упаковка из спеченных шариков оргстекла диаметром около 2 мм, запекаемых непосредственно в рабочем участке. Выявлено, что затухание «медленной» волны в пористой среде, насыщенной жидкостью с пузырьками углекислого газа, меньше, чем в той же среде, но с пузырьками воздуха. Показано, что именно колебания пузырьков обусловливают осциллирующую структуру переднего фронта «медленной» волны давления.

Шмельдерс с соавторами [4–5] экспериментально и теоретически исследовали эволюцию волн давления в пористой среде, насыщенной пузырьковой жидкостью. В качестве пористой среды использовались склеенные частицы песка или природный песчаник. Далее пористый образец насыщался пузырьковой жидкостью, которая готовилась в отдельной емкости. Показано, что, как и в работе [3], волна имеет осцилляционную структуру, связанную с наличием пузырьков. Обнаружены две продольные волны Био. Получено, что незначительное содержание газа в пузырьковой жидкости существенно влияет на динамику волн давления.

Динамика ударных волн в пористой среде, состоящей из частиц песка, склеенных эпоксидной смолой, экспериментально и теоретически исследовано в работе [6]. Рассмотрены три случая: поры, полностью насыщенные водой, поры заполнены воздухом и поры содержат смесь воды и пузырьков воздуха. Показано, что ударную трубу можно использовать для изучения отра- жения высокочастотных компонент ударной волны от пористой среды. Получено хорошее соответствие между линейной теорией и экспериментальными данными для случая, когда пористая среда насыщена водой. Когда среда насыщена частично, выявлено удовлетворительное соответствие.

В [7] численно исследовалось распространение волн давления в заполненной жидкостью цилиндрической полости в пористой среде, содержащей пузырьковую жидкость, с использованием двухскоростной, с двумя напряжениями модели пористой среды. Полученное авторами решение позволяет оценить, как влияют пузырьки газа в пористой среде на затухание и распространение сигнала в цилиндрическом волноводе.

Однако остается мало изученным вопрос распространения акустических волн в пористой среде, насыщенной газожидкостной смесью, с учетом теплообмена между газом и жидкостью. Что и сделано в данном исследовании в рамках двухфазной системы.

Основные уравнения

Примем общепринятые допущения в волновой динамике для пористых сред, заполненных пузырьковой жидкостью, и запишем систему линеаризованных уравнений [8–15]:

В p l       du l  n ^dp g       du l      Bp s

^U = 0, d x

+ Pq    — 0,+ Pq    — 0,+ Pq dt 10 dx       dt   Pg 0 dx       dt d nb      du л       4 з0

^a g 0 ^{+ a} l 0 ^{+ a} s 0 ^{— 1}

b + ⁺ n b 0     ^{— 0} , ^a g 0 ^— ~ ^na n b ,   P j ^— P j ^a j ,

6t       dx3

(«10P№ + ag0P00 ^ — К0 + al0 ^ - F, F — Fm + FM + FB , d t г 1       / о         о XI du   du I г 9   (          \\ -2

Fm — “ПЛ0 (a10Pl0 + ag0Pg0 )l "TT - "Us I,FM — “^ (a10 + ag0 )as0Ml Ul - U )a0 , d td

t

-

_x dr ^u s h=

F B ^— 6 П в ( ^1 0 ^{+ a} g 0 ) ^a s 0 a 0 ^ⁿ P l M l J — ( ^P l

-да i       0 ,         0 \dpl            I

( ^a l 0 ^p l 0 ^{+ a} g 0 ^p g 0 ) ^ ^{+ a} s 0 ^p s

0 BP s ^{s 0} 8 t

d p * d x

-

d P i d_P^

Вx ’ В t

-

—^{1 0 — 1 +} P l ^{( P} i ^{- P} i 0 ) , ^P l 0

—s ^{0 — 1 +} P s ( ^Ps ^{- P} s 0

P s 0 ) , P s ^— Pl

-

3Y Pg gw b0

*

^s as 0,

-

b0

d b q , w ^— "^, d t

**

Be 1 Bo„Bo„ ao — —--+—- s 0 В t   Es d t Ms

Be _ Bus

’ ”Bt          ’

( , d wR   3  2 I w — wR + wa, Pl 0 l b^- + -wR I — Pg I    dt    2    /

-

w

P l - ⁴Ml^ T b

⁺ 4 ⁿ M

b

\ 21

v a 0 7

, w a

Pg- Pl 0    ,„1/3 ■ pl 0 ClVg 0

Здесь Пь - число пузырьков в единице объема в j фазе; a0 , b0, w - средний радиус пор, размер пузырьков газа и радиальная скорость пузырьков, q – интенсивность теплообмена, βj – сжимаемость j фазы, пм — эмпирический параметр, фд0 - объемная доля газа в пузырьковой жидкости. Нижний индекс j = l,s относится к пузырьковой жидкости и скелету пористой среды.

Остальные обозначения соответствуют обозначениям в работе [13].

Запишем уравнение теплопроводности и граничные условия в линейном приближении [16]

ВТ            ВТ 1 Вп

P0о c. -TT — r   ^ r2 -TT +JPg, (r < b),(2)

g g dt          g    dr v7

'                     '

T g ^{— T} l , q ^{— -} ^ g

d Tg dr

7 b0

,     ( ^r <  ^b 0 ) ;

'

-T ^ — 0,   ( r — 0 ) .

d r        ^{v     7}

Ситдикова Л.Ф., Гималтдинов И.К.

Решение системы уравнений ищем в виде [8]:

р 0 , u j , p j , a j , T = A j exp Г i ( Kx - m t ) 1 , K = k + i S . j j j jg    j

После решения уравнений (1)–(3) получено дисперсионное соотношение. Ввиду его громоздкости оно не приводится. На основе полученного решения вычислены фазовая скорость и декремент затухания линейных волн.

Результаты расчета

В расчетах взяты следующие параметры при Т₀ = 300 К и р₀ = 10 5 Па. Для воздуха: p g ₀ = 10 5 Па, у = 1,4, p g ₀ = 1,17 кг/м³, p g = 1,86 - 10 ^{- 5} Пахс, X g = 0,027 Дж/(мхсхК), e g = 1006 Дж/(кгхК). Для песчаника: р ^ = 2560 кг/м³, p _s = 10 ⁸ Пахс, E_s = 3,7 - 10 ¹⁰ Пахс. Для воды: p _Z Q = 1000 кг/м³, p l = 10 ³ Пахс, C l = 1500 м/с.

Как известно пузырьковая жидкость является средой с уникальными акустическими свойствами [16]. Добавление в жидкость пузырьков газа, объемное содержание которых порядка 1-2 % кардинально меняет его акустические свойства. Из-за аномальной сжимаемости, связанной с сжимаемостью пузырьков, скорость распространения звуковых волн может уменьшиться до значения 100 м/с. Кроме этого из-за неравновесного теплообмена и акустической разгрузки импульсные сигналы в пузырьковой жидкости затухают [16]. В [16] получен закон дисперсии:

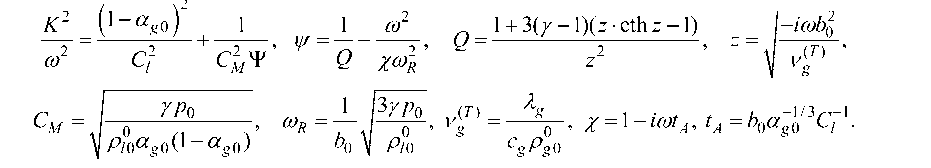
■ imb 2

1 + 3( у - 1)( z • cth z - 1)

- t m b0

(T) vg m    Cl    C2M У,    Q XmR

, %  ¹   i ^{m t} A , t A   ^b 0 ^a g 0   C l

P^^a g 0^{(1 - a} g 0 )

c g ^P g 0

На рис. 1 показаны декремент затухания S и фазовая скорость С_р для случая воды с пузырьками воздуха при b ₀ = 10 ^{- 3} м, a l ₀ = 0,99, a _{g 0} = 0,01.

На графиках видно существование трех характерных частотных отрезков, в которых существенно различается количественная и качественная картина дисперсионных кривых. Из анализа выражения (5) следует, что эффект дисперсии звука в низкочастотной области m <  m _R ( m _R -частота собственных колебаний пузырьков, частота Миннаерта [8]) определяется межфазной температурной неравновесностью. Промежуток m _R <  m < т _с ( т _с = m _R ^1 + a g ₀ р ° C l ^ P₀ ) соответствует полосе непропускания, в нем декремент затухания и фазовая скорость принимают аномально высокие значения. Величина, обратная декременту затухания, соответствует расстоянию, на котором амплитуда волн уменьшается в e раз, где e - основание натурального логарифма. Из рис. 1 видно, что при частоте, равной частоте собственных колебаний пузырьков, фазовая скорость звука минимальна и составляет приблизительно 60 м/с, а значение логарифмического декремента затухания максимально.

В работе [17] получено дисперсионное соотношение для пористой среды, полностью насыщенной жидкостью, следующего вида:

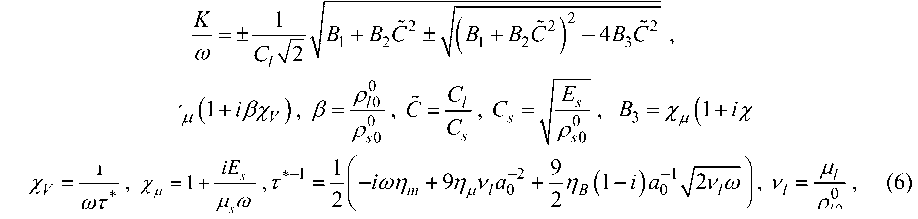
m"-ClV’)   -3-  , р0  с         ЕЁГ

B 1 = ¹ + i Z v ^a s 0 , B 2 = X p ( 1 + i PX v ) , ^в = "^т , С = 7Г , C s =. -f , B 3 = X p ( 1 + i X v ( ^a s 0 ⁺ P ^a l 0 ) ) ,

P n       C.         n.

s

^ 7 p                   7             cs тт         psm       2

где C l , C_s - фазовые скорости волны в жидкости и в скелете пористой среды соответственно.

На основе выражения (6) построены зависимости декремента затухания δ и фазовой скорости C_p «быстрой» и «медленной» волн от частоты ω на рис. 2.

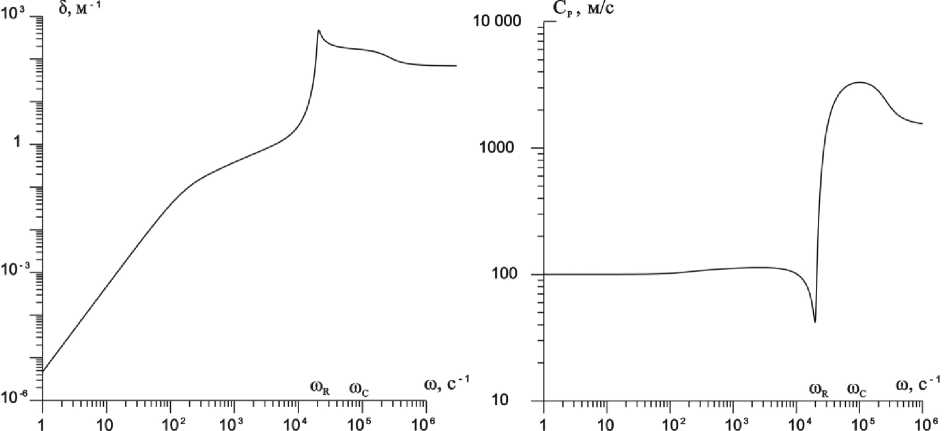
Рис. 1. Зависимость фазовой скорости C и декремента затухания δ от частоты ω для случая воды с пузырьками воздуха при b = 10^–3 м, α = 0,99

Из графиков видно, что декремент затухания для обоих типов волн увеличивается с увеличением частоты, кроме этого, коэффициент затухания «быстрой» волны для частот ω < 2 ⋅ 10 ⁵ c ^{- 1} больше, чем декремент затухания «медленной» волны. Также следует, что для частот ω < 2 ⋅ 10 ⁵ c ^{- 1} гармоническая волна затухает на расстоянии порядка 100 м. Из графика зависимости фазовой скорости от частоты следует, что для обоих типов волн с увеличением частоты скорости возрастают. Для частот ω > 10³ с^–1 оба типа волн и «медленная», и «быстрая» скорости волн стремятся к постоянным значениям. Скорость «быстрой» волны стремится к скорости звука песчанике, а скорость «медленной» – к скорости звука в воде.

На рис. 3 показано влияние теплообмена на декремент затухания δ и фазовую скорость C_p для пористой среды, заполненной газожидкостной смесью. Линии 1 построены без учета теплообмена, линии 2 – с учетом теплообмена. Характерные параметры системы a ₀ = 10 ^{- 3} м , b ₀ = 5 ⋅ 10 ^{- 3} м, α _{l 0} = 0,6, α _{s 0} = 0,39, α _{g 0} = 0,01.

Отметим, что в работе [7] показано, что при частоте собственных колебаний пузырьков и более низких частотах скорость «быстрой» и «медленной» волн в пористой среде, насыщенной пузырьковой жидкостью, ниже, а затухание выше, чем в пористой среде, насыщенной жидкостью при отсутствии газовых пузырьков. С ростом частоты скорости волн достигают тех же значений, что и в пористой среде полностью насыщенной жидкостью. Из рис. 3 также следует, что в диапазоне частот 0 < ω < ω _R скорости волн ниже, а коэффициент затухания выше для обоих типов волн, для частот ω > ω _R скорости достигают значений, соответствующих значениям заполнения пористой среды «чистой» жидкостью. Характер зависимости для «медленной» волны для пористой среды заполненной пузырьковой смесью такой же, как для «свободной» пузырьковой жидкости, полученной в работе [16], характерные диапазоны частот также разделяют «поведение» кривых коэффициента затухания и фазовой скорости. Отметим, что наиболее отчетливо теплообмен влияет на затухание «медленной» волны в диапазоне 0 < ω < ω ^{( T )} , где ω ^{( T )} = ν _g ^{( T )} I a 0² ( ν g ^{( T )} = λ g] c_g ρ _g ⁰ ₀ ). На рис. 3 данные величины соответствуют значениям ω ^{( T )} = 10 с^–1, ω _R = 4∙10³ с^–1, ω _C = 480∙10³ с^–1.

Коэффициент затухания «быстрой» волны до частоты ω имеет вид такой же, как для случая пористой среды, насыщенной «чистой» жидкостью, а при частоте ω ≈ ω происходит резкое

Ситдикова Л.Ф.,                                Задача о распространении акустических волн

Гималтдинов И.К.                    в пористой среде, насыщенной пузырьковой жидкостью уменьшение коэффициента затухания, что соответствует неустойчивому состоянию системы. На коэффициент затухания «быстрой» волны влияние теплообмена практически не влияет.

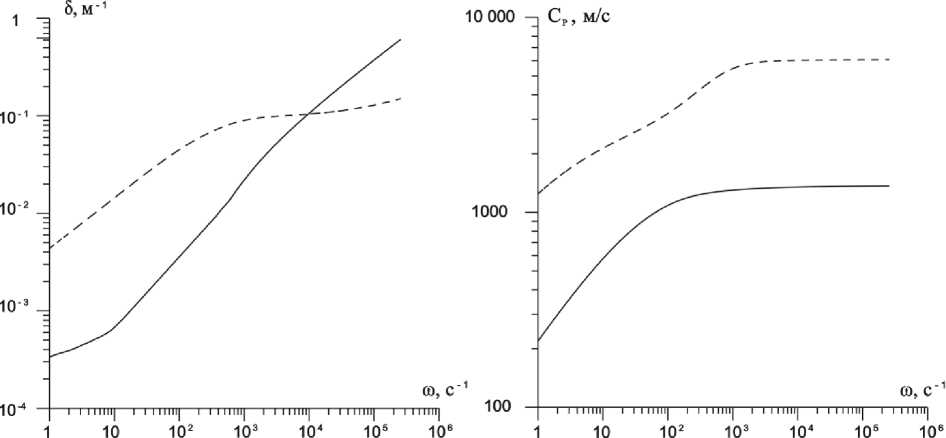
Рис. 2. Зависимости декремента затухания 5 и фазовой скорости С «быстрой» (пунктирные линии) и «медлен ной» (сплошные линии) волн от частоты го для системы песчаник-вода. Параметры: a0 = 10-3 м, al0 = 0,6, as0 = 0,4

Скорость «быстрой» волны для пористой среды, заполненной пузырьковой смесью, увеличивается в диапазоне частот 0 < ω < 103 c–1 до значения скорости звука в песчанике. Скорость «медленной» волны в диапазоне частот 0 < го < год не изменяется и составляет около 60 м/с, это значение меньше скорости звука для «свободной» пузырьковой жидкости в этом диапазоне частот. Дополнительное уменьшение скорости звука происходит из-за межфазного трения между жидкостью и скелетом пористой среды. Для диапазона частот roR < го < гоС (полоса непрозрачности) скорость «медленной» волны повышается до значения скорости в «чистой» жидкости (Ci = 1500м/с), при этом учет теплообмена приводит к более высоким значениям скорости для этого диапазона.

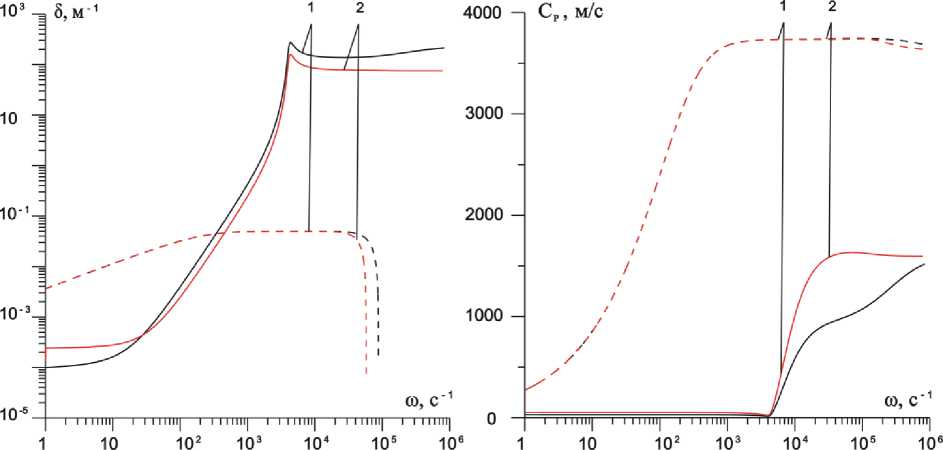
Рис. 3. Зависимости декремента затухания 5 и фазовой скорости Ср «быстрой» (пунктирные линии 1,2) и «мед ленной» (сплошные линии 1,2) волн от частоты го для системы «песчаник -пузырьковая жидкость». Линия 1 построена без учета теплообмена, линия 2 – с учетом теплообмена. Характерные параметры системы (пористая среда+пузырьковая смесь) a0 = 10-3 м, b0 = 5^10-3 м, al0 = 0,6, as0 = 0,39, ag0 = 0,01

Заключение

Теоретически исследовано распространение акустических волн в пористой среде, заполненной газожидкостной смесью, с учетом теплообмена между пузырьком и жидкостью. Установлено, что в таких средах для обеих волн характер зависимости декремента затухания и фазовой скорости такой же, как для «свободной» пузырьковой жидкости, полученный в работе [2]. Показано, что учет теплообмена влияет на декремент затухания «медленной» волны в основном для низких частот, а для «быстрой» волны учет теплообмена не влияет на процесс затухания. Стоит отметить, что во всем диапазоне частот на скорость «быстрой» волны межфазный теплообмен между жидкостью и газом влияет несущественно. Для частот 0 <  го <  ^ скорость «медленной» волны не зависит от учета теплообмена, а в области полосы непропускания учет теплообмена приводит к более высоким значениям скорости звука.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-31-60015.