Задача об образовании гидрата в слое снега при нагнетании холодного газа

DOI:

Природный газ – первичный топливно-энергетический ресурс России. В последнее время довольно актуальной и перспективной является проблема подземного хранения газа в связи с неравномерностью и сезонностью его потребления, а также ростом объемов добычи газа. В естественных условиях довольно привлекательным представляется создание хранилищ с законсервированным газом в виде газогидратов, поскольку в 1 м3, например, гидрата метана содержится около 180 м3 газа и 0,8 м3 воды [5]. Возможность создания таких газогидратных хранилищ в реальных условиях подтверждается геологическими и экспериментальными исследованиями [11; 20]. Примером таких хранилищ в реальных условиях могут служить гидратные образования в породах криолитозоны, а также на суше и шельфе Арктики. Таким образом, технология подземной консервации газа в газогидратном состоянии может обеспечить высокий уровень безопасности хранения и транспортировки газа, не требуя больших экономических затрат [2; 3; 7; 12].

В экспериментальных работах [11; 21–24] показано, что основным механизмом гидратооб-разования, в диапазоне отрицательных температур, является диффузия газа через формирующуюся корку газового гидрата к границе контакта лед – гидрат. Диффузионная теория образования гидрата из ледяного порошка представлена в работе [1]. В существующих на сегодняшний день моделях процесса образования гидрата [1; 18; 19] имеется довольно много эмпирических параметров, которые отвечают за кинетику гидратообразования. В работе [18] выявлено, что на интенсивность роста гидратной пленки влияют качество и состав льда и газа, наличие различных солей, а также примесных частиц и капиллярных добавок. Из экспериментальных работ [21–24] известно, что при образовании гидрата метана, в диапазоне отрицательных температур, из поли-дисперсного порошка ледяных сферических частиц наблюдается зарождение гидратных пятен, с их последующим ростом, на поверхности ледяных сферических частиц и дальнейшее увеличение гидратного слоя, лимитирующегося диффузией газа через гидратную оболочку к ледяному ядру. Работы [10; 14; 17] посвящены математическому моделированию процесса образования гидрата в пористых пластах при нагнетании газа. Например, модель образования гидрата с использованием диффузионной кинетики рассматривается в работе [14]. Численные исследования образования газогидрата в равновесном режиме, с учетом фазовых переходов, были проведены в работах [9; 10; 17]. Ввиду этого, большой интерес представляет изучение таких вопросов, как описание кинетики и установления механизмов процесса гидратообразования, а также создание технологий консервации газа в гидратное состояние, являющееся довольно выгодным и безопасным.

Целью данной работы является построение и развитие математической модели процесса нагнетания холодного гидратообразующего газа в массив снега, насыщенный тем же газом.

Постановка задачи и основные уравнения

Пусть имеется горизонтальный снежный массив в начальный момент времени ( t = 0) насыщенный снегом и газом, при температуре T ₀ и давлении p ₀, удовлетворяющие условиям фазового равновесия системы «газ + снег + гидрат» T₀ = T s ( p ₀ ) . Причем начальная температура массива находится в отрицательной области, а исходное давление меньше нагнетаемого. В некоторый момент времени ( t >  0) через левую границу массива происходит нагнетание газа при температуре T_e и давлении p_e , соответствующие термобарическим условиям образования гидрата.

Для определения зависимости равновесной температуры T_s ( p ) от текущего значения давления примем выражение [4; 13]

T s ( Р ) = T 0)

( „ ^

+ T. ln -p l Р(s0) )

где T _{( s 0)}, p _{( s 0)} – равновесные значения температуры и давления системы «газ + снег + гидрат»; T _* – эмпирический параметр [3].

В рамках принятых допущений запишем уравнения сохранения масс для снега, газа и гидрата в виде [6]

—(Р0 S,) = - J, dt a „ a „

- (P°S) + -(PSgU) = - J,(2)

д' tX

I (Ph Sh)=Jh, о t где pj,Sj (j = i,g, h) - соответственно истинные плотности и относительная объемная насыщенность фаз; υg – скорость газа; Ji, Jg – интенсивности расхода снега и газа, которые идут на образование гидрата с интенсивностью Jh в единице объема среды. Здесь, и в дальнейшем, нижние индексы j = i, g, h соответствуют параметрам, относящимся к снегу, газу и гидрату.

В связи с тем что газогидрат метана имеет клатратную структуру, с массовым содержанием газа G , для интенсивностей J_i , J_g и J_h должны выполняться следующие условия

J g = GJ h , J= (1 - G ) J h .

Пренебрегая баротермическим эффектом и полагая равными температуры составляющих фаз ( T_g = T_h = T = T ) , запишем уравнение притока тепла в следующем виде

a t    o a t pc^:+P SPs U ^ = dt    g g g g dx

⁺ J h l h ,

pc = р , Sc + P h S h C h + P g S g C g , X = S i X i + S h X h + S g X g .

Здесь l_h – удельная теплота образования гидрата из снега, отнесенная на единицу его массы; ρc и λ – удельная объемная теплоемкость и теплопроводность системы «газ + снег + гидрат» соответственно; c j , X j ( j = i , g , h ) - соответственно удельная теплоемкость и теплопроводность фаз.

Полагаем, что снег и гидрат несжимаемы, а газ – калорически совершенный

P i ⁰, P h = const , p = p _g ⁰ R g T .                                    ⁽⁵⁾

Процесс фильтрации газа подчиняется закону Дарси

S g υ g

kg d p p_g a x ’

где µ_g и k_g – динамическая вязкость газа и коэффициент проницаемости массив а.

Из уравнения сохранения масс (2) для снега и гидрата с учетом условия (3) получим

S i P i + ( 1 - G ) S h P 0 = const .                                 (7)

В исходном состоянии ( t <  0) примем S_h = 0 и S i = S i ₀, тогда из (7) имеем

Sh =

ρ i ⁰

P h ( 1 - G )

( S o - S ) .

Для насыщенностей фаз должно выполняться следующее условие

S i + S h + S g = 1.

Подставляя выражение (8) в кинематическое условие (9), получим

1 - S. - SГ,

Sh =    n 0 i 01 A Si= Si0 - P (1 - G) Sh.(10)

1 - Ph (1 - G) ,

^ρ i ⁰

Здесь через текущее значение газонасыщенности S_g однозначно определяются текущие величины гидратонасыщенности S_h и снегонасыщенности S_i .

Диффузионная кинетика гидратообразования

Пусть слой снега представляет собой сферические частицы льда с исходным радиусом a_{i 0}. Будем полагать, что интенсивность гидратообразования лимитируется диффузией газа через гидратную корку, образующуюся на границе контакта лед – гидрат.

Рассмотрим некоторую одиночную гидратно-ледяную частицу сферической формы, с внешним радиусом ai0 и внутренним радиусом ah ледяного ядра, изменяющимся в процессе образования гидрата из газа и снега. Текущее значение внутреннего радиуса ah гидратной частицы определяется через текущее значение снегонасыщенности ah = a 3 Si! S .

Так как скорость образования гидрата определяется диффузией газа через образовавшийся гидратный слой между газом и снегом, то такой газ со средней плотностью р g в гидрате будем называть подвижным газом, не входящим в состав гидрата (диффундирующим газом). Запишем уравнение диффузии [14; 15]

д р g = D g д д t r ² д r

( r 2 д р д V д r

( a h <  r <  a ) .

Квазистационарное решение уравнения (11), полагая, что дрg ]бt = 0, при следующих граничных условиях р g=pg (.),r=a^;P g=0, r=ah,                                 (12)

имеет вид

, _ ^p g(s) ^{( r} - ^a h ) ^p g

r 1

V

—

,

ah- ai 0 )

где p g ( _s ) - плотность насыщения подвижного газа в составе гидрата.

Запишем выражение для определения потока массы подвижного газа к поверхности контакта между льдом и гидратом, отнесенного к единице площади ледяного сферического ядра в виде [6]

j g

^- D g

(дрк ^ V дr 0 ah

.

Подставляя в (14) решение (13), получим выражение для интенсивности потребления газа, который идет на гидратообразование, отнесенной к единице площади ледяной частицы

js =

D g ρ g ( s )

ah

1 -

ah

a i 0 V

Как показывает численный анализ, результаты, полученные с учетом уравнения диффузии в полном его виде, достаточно хорошо совпадают с его аналитическим решением [16].

Чтобы определить интенсивность расхода газа J_g , отнесенного на единицу объема, необходимо определить число ледяных сфер с радиусом a_{i 0} (в единице объема) как

n =

3 S i 0 4 πa_i ³ ₀ ^,

а также удельную площадь поверхности контакта, между фазами льда и гидрата в виде

S = 4na 2 n .

Подставляя в выражение для потока массы (14) решение уравнения диффузии (13), с учетом количества ледяных сфер (15) и удельной площади поверхности контакта (16), получим выражение для интенсивности расхода газа, отнесенную на единицу объема

J g

3 S i 0 Dρ

g

^a i ² 0

a i 0

—

л

1 ,

D =

D₈ ^p g ( s )

.

к

ah

V

ρ

g

Здесь D – эмпирический параметр, приведенный коэффициент диффузии для газа, отвечающий за кинетику образования гидрата.

Принятая в работе предельная схема образования гидрата описывает процесс перехода снега в состав гидрата путем введения лишь одного эмпирического параметра – приведенного коэффициента диффузии D . Рассматриваемая кинетика, с точки зрения описания качественной и количественной картины процесса образования гидратной частицы из газа и снега, довольно хорошо согласуется с экспериментальными данными и расчетами, проведенными в работах [18; 21–24].

Равновесный режим гидратообразования

Пренебрегая диффузионным сопротивлением, в выражении (17) будет иметь место равновесная по фазовым переходам T = T_s ( p ) фильтрация. Это будет соответствовать предельному случаю, когда приведенный коэффициент диффузии стремится к бесконечности ( D ^ да ) . Следовательно, интенсивность фазовых переходов будет определяться из уравнения энергии (4).

Из уравнения сохранения масс для гидрата (2) интенсивность гидратообразования Jh в единице объема среды запишем как т _   дSh

^Jh    ^P h д.

д t

Наибольший практический интерес представляют случаи, когда слагаемыми, отвечающими за конвективный и кондуктивный перенос тепла, можно пренебречь [14]. Тогда уравнение баланса тепла (4) с учетом (18) можно записать в следующем виде

д , _    1 9S

— ⁽ PcT ) ^_ Р . 1 .— .

д t                д t

Пренебрегая переменностью объемной теплоемкости ρc всей системы, получим

S h _ -^Pc - ( T s ( P ) — T o ) ,( P 0 <  P <  P e ). ρ_hl_h

Выражение (20) определяет гидратонасыщенность как функцию от текущего давления в области отрицательных значений температур (T <  T ⁽⁰⁾).

Второе уравнение для сохранения массы газа системы (2), с учетом условия фазового равновесия (1), закона Дарси (6), выражения (19) и уравнения состояния газа (5), можно привести к виду

д

Г SgP

\

д11 RgTs (P)

+

pcG дTs (P) __d

p   kg ^д p

l h      д t      д x V R g T s ( P ) P g д x ₇

Отметим, что соответствующее значение распределения температуры связано с давлением условием фазового равновесия (1).

Уравнение сохранения масс для снега с учетом уравнения для газа системы (2) и соотношений (3) приведем к виду p° ^SL _—(1 — G ) ph0 ^Sh i д t       V h     д t ’ которое на основе кинематического условия (9) запишется как

дSg _ д t

^ ph(1 — G)

—

\

1® h

V     P i

дt .

Если в исходном состоянии ( t <  0) гидратонасыщенность равна нулю ( S_h = 0), а газонасы-щенность равна исходной S_g = S_{g o}, а также, интегрируя выражение (22), получим соотношение для текущей газонасыщенности

S g _ S g о

—

(

V

—

ph(1 — G)

Pi    7

^S h .

Предположим, что снег полностью перешел в состав гидрата, то есть в уравнении (8) S_i = 0, то получим выражения для определения максимальной гидратонасыщенности S_{h (max)}

^u h (max)

ρ i ⁰

P 0 ( 1 — G )

^S i 0 .

Подставляя (23) в выражение (20), получим максимально возможный нагрев системы «газ + снег + гидрат» за счет тепла, выделяемого в результате гидратообразования

ρhlh

■^шах)    pc Sh(max), где

A T (max) _ T s ( P (max) ) — T

Тогда значение давления, при котором снег полностью переходит в гидратное состояние p _(max), определим согласно выражению (1):

P (max) = P 0 e ^X P ^{( A T} (max) / ^T * )•

Отметим, что давление нагнетаемого газа не должно превышать равновесного значения давления p s (T ⁽⁰⁾), которое соответствует температуре плавления льда (T ⁽⁰⁾ = 0⁰ C ) ( p_e <  p s (T ⁽⁰⁾)). Иначе, для получения непротиворечивого решения, необходимо будет рассматривать область, насыщенную газом, гидратом и водой. Если значение давления нагнетаемого газа p_e меньше максимально возможного давления p (mx) ( p e <  p _(max)), то в массиве будет возникать зона, насыщенная газом, снегом и гидратом, то есть будет происходить частичное гидратообразование. Если давление нагнетаемого газа p_e больше максимально возможного p _(max) и при этом меньше равновесного значения p s ( T ⁽⁰⁾) ( p _(max) <  p_e <  p s ( T ⁽⁰⁾)), что соответствует случаю полного гидра-тообразования, то возникнет подвижная фронтальная граница x = x _{( n )}, разделяющая массив на две области: область, примыкающая к левой границе x = 0, насыщенная фазами газа и гидрата, в которой снег полностью перешел в состав гидрата, и область, состоящая из снега, газа и гидрата. Следовательно, на подвижной границе x = x _{( n )} должны выполняться следующие граничные условия:

_х = _х   у о) = _р⁽²⁾        j ⁽¹⁾ _/'■'' __т    _^д^дp₊ kK LE— ₌ о

Х X( n ) : p p     p(max),                (max), ^ dx         dx     , где верхние индексы (1) и (2) соответствуют двум областям.

Численная реализация

Образование гидрата по диффузионной кинетике

Рассмотрим процесс фильтрации газа в слое снега протяженностью x 0 (0 <  x <  x ₀) в начальном состоянии, который насыщен газом метаном. В исходном состоянии давление p ₀ и температура T ₀ в слое снега удовлетворяют условиям фазового равновесия системы «газ + снег + гидрат». В некоторый момент времени ( t >  0) через левую границу слоя снега ( x = 0) происходит нагнетание газа при давлении p_e и температуре T_e , соответствующие условию гидратообразования.

Тогда начальные условия можно записать в виде

T = To, p0 = ps (To ), S,= Si0, Sh = 0, Sg = 1 - Si0, (t = 0,0 < x < x0).(24)

Полагаем, что потоки массы и тепла через правую границу ( x = x ₀) отсутствуют [14; 16]

— = 0, ^P = 0,(t > 0, x = x0).(25)

dxd

Условия на левой границе ( x = 0) имеют вид

T = Te, p = pe, (t > 0, x = 0).(26)

Система уравнений (1)–(17) с начальными (24) и граничными условиями (25) и (26) была решена методом конечных разностей с использованием явной схемы [8].

Образование гидрата в равновесном режиме

Рассмотрим случай, когда начальное давление p ₀ и температура T ₀ находятся на линии фазового равновесия. Полагая, что температура нагнетаемого газа T_e равна равновесной температуре фазовых переходов T_s ( p_e ) для давления p_e , тогда условия на левой границе ( x = 0) запишем в виде

T = T e = T s ( Р е ) , P = P e ,( t >  0, * = 0).                             (27)

Уравнение (21) с начальными (24) и граничными условиями (25) и (27) решено также методом конечных разностей по явной схеме.

Результаты численных расчетов

Для теплофизических параметров системы «газ + снег + гидрат» приняты следующие значения: G = 0.12, R g = 520 Дж/(кг^К), p° 0 = 910 кг/м³, p° i = 900 кг/м³, c i = 2100 Дж/(кг^К), c g = 1560 Дж/(кг-К), c h = 2050 Дж/(кг-К), X g = 0.03 Вт/(м-К), X i = 2.21 Вт/(м-К), X h = 0.5 Вт/(м-К), k g = 10 ^{- 9} м², p_g = 10 ^{- 5} Па-с, l_h = 1.45 ■ 10 5 Дж/ кг, D = 10 ^{- 12} м²/с.'

Значения параметров, входящие в условие фазового равновесия (1), принимались равными: T _* = 30 К, T _{( s 0)} = 263 К, p _{( s 0)} = 1,86 МПа [3; 4].

Величины, характеризующие исходное состоянии системы «газ + снег», температура, давление и снегонасыщенность массива принимали значения: T ₀ = 200 К, p ₀ = p_s ( T ₀) = 0,23 МПа, S_{i 0} = 0,3. Протяженность снежного слоя составляла x ₀ = 10 м. Нагнетание газа происходило при температуре T_e = 200 К и давлении p_e = 2,5 МПа, соответствующих условиям образования гидрата.

На рисунке 1 показана динамика давления ( а ), температуры ( б ), гидратонасыщенности ( в ) и снегонасыщенности ( г ) в точке массива x = 5 м при различных начальных значениях снегонасы-щенности. Из графика видно, что снег полностью переходит в состав гидрата, при этом увеличение исходной доли снега в массиве приводит к более интенсивному его переходу в состав гидрата, что обусловлено ростом потребления газа, необходимым для гидратообразования, при заданной интенсивности его нагнетания.

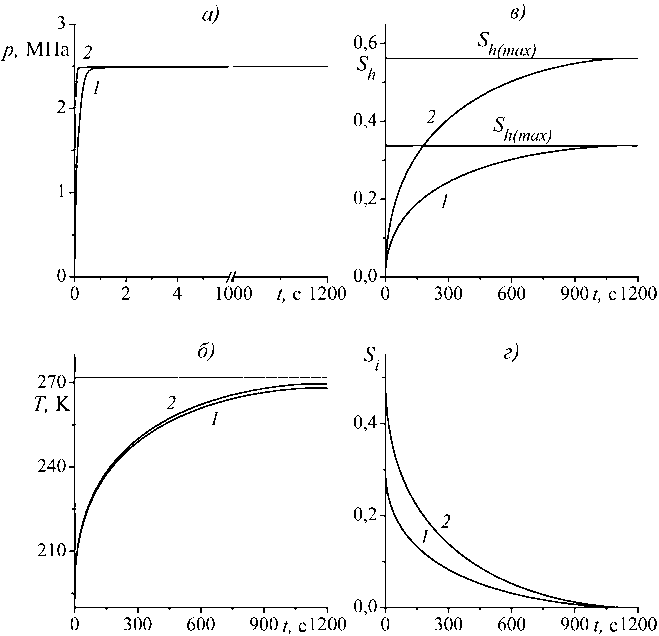
Рис. 1. Динамика давления, температуры, гидратонасыщенности и снегонасыщенности в точке х = 5 м при различных начальных значениях снегонасыщенности ( 1 – S_{i 0} = 0,3 и 2 – S_{i 0} = 0,5)

На рисунке 2 показана динамика давления ( а ), температуры ( б ) и гидратонасыщенности ( в ) в точке x = 5 м при различной проницаемости массива. Справа представлены увеличенные фрагменты начального этапа образования гидрата. Линия 1 соответствует значению проницаемости к = 10 ^{- 9}м², а линия 2 - к = 10 ^{- 10}м². Установлено, что чем ниже значение проницаемости, тем интенсивнее происходит гидратообразование. Установлено, что при проницаемости k_g = 10 ^{- 10}м² давление в снежном массиве достигает граничного значения p_e практически одновременно с процессом полного гидратообразования.

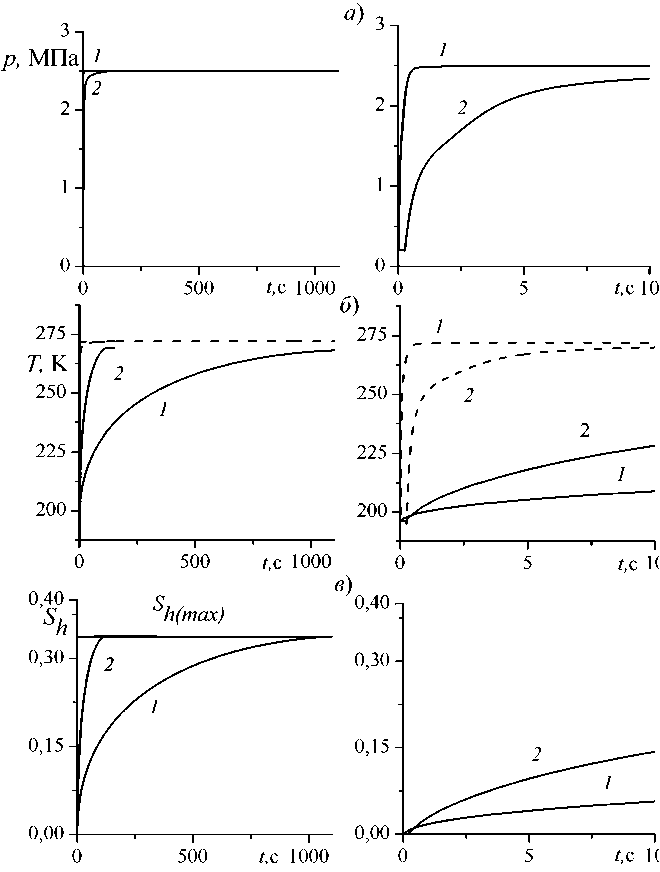
Рис. 2. Динамика давления, температуры и гидратонасыщенности в точке х = 5 м для диффузионного режима при различных значениях проницаемости газа (1 – kg = 10–9 м2 и 2 – kg = 10–10 м2)

На рисунке 3 представлена динамика давления (а), температуры (б) и гидратонасыщенно-сти (в) в точке массива x = 5 м при отмеченных выше параметрах, определяющих начальное состояние снежного массива и нагнетаемого газа. Линии 1 и 2 соответствуют диффузионному режиму, линия 3 – равновесному режиму. В случае диффузионной схемы для приведенных коэффициентов диффузии были приняты следующие значения: D = 10–11 м2/с (линия 1) и D = 10–12 м2/с (линия 2). Часть фрагмента на первых секундах гидратообразования представлена справа. Интенсивность процесса образования гидрата характеризуется приведенным коэффициентом диф- фузии D. Равновесный режим формально реализуется в том случае, когда приведенный коэффициент диффузии стремится к бесконечности. Из рисунка 3 следует, что с ростом D система стремится к равновесному по фазовым переходам режиму, что обеспечивает наиболее быстрый темп перехода снега в гидратное состояние.

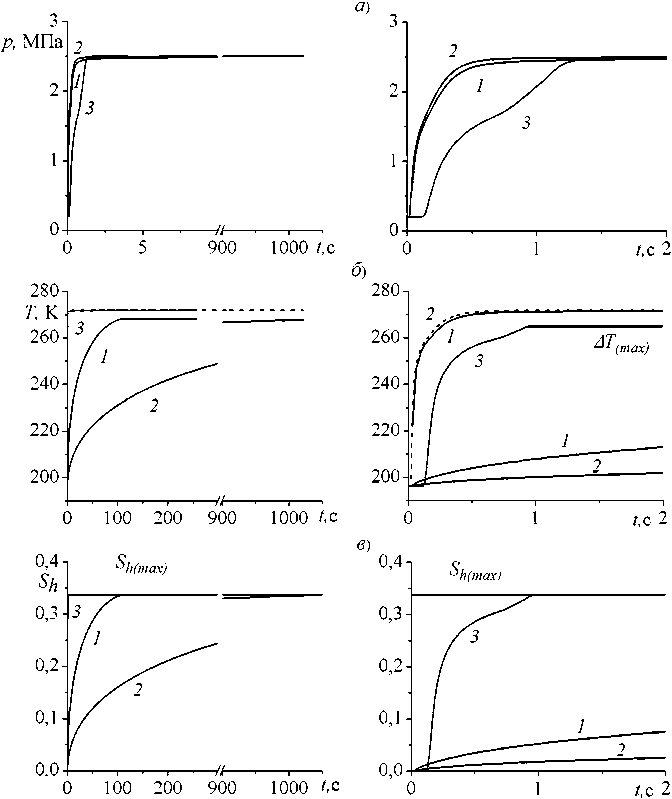
Рис. 3. Динамика давления, температуры и гидратонасыщенности в точке х = 5 м для диффузионного (линии 1 – D = 10–11 м2/c и 2 – D = 10–12 м2/c) и равновесного (линия 3) режимов

На рисунке 4 представлена аналогичная зависимость, что и на рисунке 1, при различных начальных значениях снегонасыщенности и проницаемости для равновесного режима. Начальная температура и давление принимались равными T0 = 200 К, p0 = ps(T0) = 0,23 МПа, нагнетание газа происходило при температуре Te = 272 К и давлении pe = ps(Te) = 2,5 МПа. На рисунке линия 1 соответствует значению начальной снегонасыщенности Si0 = 0,3 и проницаемости kg = 10–9 м2. Линия 2 характеризует динамику процесса гидратообразования при начальной снегонасыщенности Si0 = 0,5 и проницаемости kg = 10–9 м2. Линия 3 соответствует значениям Si0 = 0,3 и kg = 10–10 м2. Видно, что чем выше начальное значение снегонасыщенности, тем больше гидрата образуется в массиве. Из рисунка 4 следует, что в случае равновесного режима при более высоких значениях проницаемости увеличивается интенсивность гидратообразования. Видно, что при достижении давления p(max) возникает подвижная граница, разделяющая массив на две зоны: зона, насыщенная газом и гидратом, и зона, состоящая из снега, газа и гидрата. Следует отметить, что при достижении границей x(n) правой границы массива (x = x0) процесс гидратообразования прекра- щается, и в последующем будет происходить только изотермическая фильтрация газа, пока давление в массиве, насыщенном газом и гидратом, не принимает граничного значения давления pe.

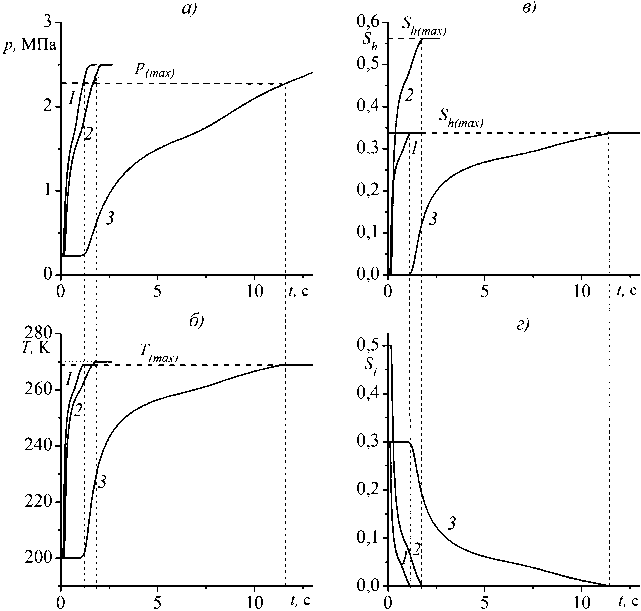
Рис. 4. Динамика давления, температуры, гидратонасыщенности и снегонасыщенности в снежном массиве для равновесного режима при различных начальных значениях снегонасыщенности (1 – Si0 = 0,3 и 2 – Si0 = 0,5) и различной проницаемости газа (1 – kg = 10–9 м2 и 3 – kg = 10–10 м2)

Заключение

В работе построена математическая модель нагнетания гидратообразующего газа в массив снега, который частично насыщен тем же газом. Определено, что процесс гидратообразова-ния может протекать как в диффузионном, так и в равновесном режимах. Получена динамика давления, температуры, гидратонасыщенности в массиве, при полном переходе снега в гидратное состояние. Был проведен анализ влияния таких параметров, как исходная снегонасыщен-ность, проницаемость массива и приведенный коэффициент диффузии на процесс гидратообразо-вания. Выявлено, что с увеличением начальной снегонасыщенности происходит интенсивный переход снега в гидратное состояние. Установлено, что с ростом приведенного коэффициента диффузии D система стремится к равновесному по фазовым переходам режиму, что обеспечивает наиболее быстрый темп перехода снега в гидратное состояние.