Задача определения ядра в одномерном уравнении третьего порядка Мура - Гибсона - Томпсона с памятью

The Moore–Gibson–Thompson theory was developed beginning from a third order differential equation, constracted in the context of some consideration related fluid mechanics. Subsequently the equation was considered as a heat conduction equation because it has been obtained by considering a relaxation parameter into the type III heat conduction [1–4]. Since the apparition of the Moore–Gibson–Thompson theory, the number of studies on this theory has increased considerably. The Moore–Gibson–Thompson equation also modifies and defines equations for thermal conduction and mass diffusion that occur in solids.

Inverse problems for integro-differential equations are important mathematical problems in science and engineering. They hav e wide applications in computed tomography, biology,

• ^# The research was executed at North-Caucasus Center for Mathematical Research of the Vladikavkaz Scientic Center of the Russian Academy of Sciences with the support of the Ministry of Science and Higher Education of the Russian Federation, agreement №075-02-2024-1379.

(О 2024 Boltaev, A. A., Durdiev, D. K. and Rahmonov, A. A.

mineral exploration, acoustics, communication theory, signal processing, medical imaging and many other fields. Fundamentals of the theory of inverse problems for mathematic physical equations were developed by many authors, especially the works [5–9] (see also the references in them).

Inverse convolution kernel problems for linear parabolic and hyperbolic integro-differential equations of the second order were considered in a number of papers (see, for example, [10– 16]). In [10–12], the authors have discussed the local existence and global uniqueness of the recovering convolution kernels in hyperbolic integro-differential equations. The works [13, 14] deal with the problems of identifying the one-dimensional kernel of the hyperbolic integrodifferential equation with a source of explosive type. A wide class of inverse problems for identifying one- and multidimensional convolution kernels in second-order hyperbolic integrodifferential equations was studied in the recently published monograph [15]. The paper [16] studies the global solvability of two kernels determination problems in the parabolic integrodifferential equation. For close problems related to other models, we refer to [17–20].

In the work [21], it is considered the derivation of the MGT equation and the list of references therein. These equations are the sub ject of several recent research due to their wide range of applications in the medical and industrial fields of high intensity ultrasound waves. The well-posedness of linearized MGT equation and the uniform decay of its energy is studied under suitable functional setting and initial-boundary conditions in [22]. Inverse coefficient problem for MGT was treated in [23], where it is proved uniqueness and also showed stability by Carleman estimates.

In the works [24, 25], the authors investigate the inverse problems of determining kernel function and three unknown parameters by using the Laplace transform. The research method in these papers is local, but it uses the fact that the direct problem is considered with the Neumann type boundary conditions.

In this paper, we propose a method for studying the determination of the convolution kernel in MGT equation using the Fourier spectral method and the method of integral equations. The results obtained are of a local nature. However, we can prove local solvability theorem for inverse problem, taking into consideration that the nonlinearity has a convolution structure (see [26, 27]).

We consider the one-dimensional MGT equation:

u ttt + u tt - u xxt

- u xx

t

+ У g(t - т)u xx (x,T ) dT = 0 ,

in the domain

D = (0 , 1) x (0 ,T ] , where T >  0 is an arbitrary fixed number with initial conditions

u(x, 0) = a(x),   u _t (x, 0) = b(x),   u _tt (x, 0) = c ( x ) ,   x G [0 , 1] ,               (2)

and boundary conditions

u(0,t) = u(1,t)=0, t G [0 ,T ] .                              (3)

The problem of determining a function u(x, t) G C 2^?3 (D) П C°t ( D ) that satisfies (1)—(3) with known functions a(x), b(x), c(x) and g( t) will be called the direct problem.

In the inverse problem, it is required to determine the function g (t) , t G [0 , T ] , using overdetermination conditions about the solution of the direct problem (1)–(3):

where x o G (0 , 1) is fixed number and h ( t ) is sufficiently smooth given function.

The rest of this paper is organized as follows. In Section 2, we present our investigations on the direct problem (2)–(4). We find differential properties and stability estimates for the solution of this problem. Section 3 devoted to the formulation and proof of the main results of this work, which are the theorems of local existence and uniqueness for solution of inverse problem. Section 4 contains the conclusion.

2. Investigation of Direct Problem

As we shall use separation of variables methods, let us denote by λ _n its eigenvalues and eigenfunctions by X _n ( x ) , i.e.,

Х П ‘ ( х ) + A n X n ( x )=0 in (0 , 1) ,

X n (0)=0 , X n (1)=0 ,   n = 1 , 2 ,...

It is know that

An = (nn)2, Xn = sin(nnx), and the set {Xn}n^i is a basis for L2(0,1).

The solution u ( x,t ) , can be written as

∞

u(x,t) = ^Un(t)Xn(x) in L2(0,1), n=1

where

u _n (t) =2 У u(x,t)X _n (x) dx.

Multiply (1) by X _n ( x ) and integrate over (0 , 1) , we have

2 У u ttt (x,t)X n (x) dx + 2 У u_tt(x,t)X n (x) dx

t

- 2    u xxt ( x, t ) X n ( x ) dx

- 2 У U xx (x,t)X n ( x ) dx + 2 у g(t -

т ) J U xx (x,t)X n (x) dxdT = 0 ,

which reduces to the functional equation. Used to (5), (6) and (8), we get

t un(t) + u'n(t) + Anu'n(t) + AnUn(t) = An У g(t - т)ип(т) dT.

From the initial conditions (2), we arrive at the following

A n := u n (0) = 2 У a(x)X n (x) dx, B n := и П (0) = 2 J b(x)X n (x) dx,

C n := u n (0) = 2 У

c ( x ) X n ( x ) dx,

n >  1 .

Let us consider the third-order ordinary differential equation (9) with the right-hand side of the form A n / 0 g(t — т)u _n (r ) dT with the Cauchy data (10), (11). Solving this problem for each fixed n ^ 1 , it is easy to conclude that it is equivalent to the following Volterra-type integral equation:

¹ u n ^(t) — ,     .

^A n + ¹

T ^ n ^{( A} n + B n ) + 7= ⁽ B n + C n ) ) sin TT i t λ _n

+ A—+1 [(AnAn + Cn) e t + (An — Cn) cos T^ntj tτ

+ T“nT I F n (t — T ) [ g(r — s)u n (s) ds dr,    (12)

^A n ^{+ 1} J          J

where

F n ^{(t) —} e t +

λ n

sin y/Xnt

— cos y/Ant.

We now obtain sufficient conditions for the given functions a ( x ) , b(x) , c(x) and kernel g(t), under which the integral equation (12) has a unique classical solution.

Estimating each function u _n (t), for t G [0 ,T ] , we get the following integral inequalities

t

1            3

^{| u} n ^{( t ) |} C ^{2 | A} n | +

A= | B n | + ~ | C n | + ²ll gll J^(t - ^T)lu n ^{(r ) | dT}, nn   ₀

where ||g || — max _{t e} [Q ,T ] | g ( t ) | . Applying the Gronwall lemma here, we obtain

| u n ( t ) | C

^{2 | A} n | +

1                3

7= | B n | + -| C n |

e ll g ll t ² ,

t G [0 ,T ] .                (13)

Calculating the first derivative of (12) and using (13), we find an estimate for u' _n (t) :

\ ^u n ^(t) \ ^{C 2} | ^A n | ⁺ | B n | ⁺

7= i C n ¹

+ ^ A n ^ g ^ t ^{2 2} | A n | +

1                3

7 A = | B n | + - | C n |

e ^ g ^ t ² ,

t G [0 , T ] .

As above the second derivative of (12) taking into account (13), u'n ( t ) estimated as follows:

\ ^u n ^{( t )} I ^{C 3} V ^A n \ A n \ + 7 ^A nn | B n | + ³ | C n |

+ ^2A n \\ 9 \\ t 2 [^{2 | A} n | +

λ n

I B n | + I- I C n ll e^ λ_n

t G [0 ,T ] . (15)

Estimate for u n ( t ) is obtained by the equation (12) using (13). It has the form

\ ^u n ^(t) \ ^{C 2 A} n | A n | + ^A n | B n | + ² T ^A n | C n |

+ An llgllt [1 + TTit)  2 |An| +--77= |Bn| + 7“\Cn\  e llgllt2, t G [0,T].       (16)

λ n        ^λ n

Combining the (13)–(16), we get

Lemma 1. The following estimates are valid t G [0 ,T ] and for each n G N :

| u n ( t ) I С ^e0 ( | A n | +-- 1 B n | +-- dC n l^ ^{,    | u} n ^{( t ) |} ^ ^в 1 fn l A n l + I B n l ^{+ | C} nP) ,

\ П      П2    J               \              nJ lun(t)l С в2 (n21Anl + п|Bnl + |Сп|) ,   lun‘(t)l С в3 (n3lAnl + n21Bnl + nlCnl) , where ei, i = 1, 2, 3, are positive constants independent of a(x), b(x), c(x), g(t) and number T.

Formally termwise differentiating the series in formula (7), we get the following series:

∞∞

U tt = ^ u n ( t ) sin л/A n x, u ttt = ^ u 'n (t) sin yAn x, n =1                        n =1

u _xx

∞

^ A n U n (t) sin yAnx, n =1

u _xxt

∞

^ A n u '_n (t) sin yAn x.

n =1

In view of Lemma 1 series (7) and (17), (18) with any ( x,t ) G D are majorized by the series

∞ в E (n3lAnl + n2|Bn| + n|Cn|) , в := max ei• n=1

Here is the following auxiliary lemma:

Lemma 2. If the conditions are met

a ( x ) G C ³ [0 , 1] ,    a^IV ( x ) G L ₂ (0 , 1) ,   a (0) = a (1) = a ‘‘ (0) = a ‘‘ (1) = 0 ,

b ( x ) G C ² [0 , 1] ,   b ‘‘‘ ( x ) G L 2 (0 , 1) ,   b (0) = b (1) = b ‘‘ (0) = b ‘‘ (1) = 0 ,

c(x) G C 1[0,1],   c‘‘(x) G L2(0,1), c(0) = c(1) = 0, then the following representations are valid:

An =        An4), Bn =        Bn3),   Cn =   Cn2);

λn λn             λn λn here An3, Bn3 and Cnn2 are coefficients of the expansion of functions a(x), b(x) and c(x) in series with respect to the function system {2; cos VAnx} and {sin vAnx}, such that

∞∞∞

E lAn4)l2 С |a(IV31к(0,1), ЕКА С 1Г1Ь(0,1), \ С Hc"llL2(0,1),(21)

n=1                          n=1

where -d z a ( x ) := a IV ( x ) .

Integrating by parts in the integral for An four times, Bn three times and Cn two times (see (10) and (11)) taking into account the conditions of Lemma 2, we obtain equalities (20). Inequalities (21) are based the Bessel inequalities for the coefficients of the Fourier expansions of the functions aIV(x), b‘‘‘(x) and c’’(x) in the system of cosines {2; cos \/Xnx} and sines {sin \/Anx} on the interval [0,1], respectively. If the functions a(x), b(x), and c(x) satisfy the conditions of Lemma 2, then, due to representations (20) and (21), series (7) and (17), (18) converge uniformly in the D, therefore, function (7) satisfies equation (12). Under the conditions of Lemma 2 and g(t) G C[0, T], this is a classical solution of the Cauchy problem (9)–(11).

The proven assertion implies the next theorem.

Theorem 1. If a ( x ) , b(x), c ( x ) satisfies conditions of Lemma 2 and g(t) G C [0 ,T ] , then problem (1) - (3) has a unique solution, which is defined by series (7) and belongs to class u(x,t) G C^^D ) n C£ D).

Now, we will give some estimates for the solution and its first derivative of the direct problem (1)–(3).

Let u _n be solution of the integral equation (12) corresponding to the functions A n , B n , C _n , and g . Let us derive an estimate for the norm of the difference between the solution of the original integral equations (12) and the solution of this equation with functions A _n , B _n , C _n , and g . After making obvious estimates, we have

^{| u} n | C ² | A n | +

1 I D I 3 | /— | 7== ¹ B n ¹ + 7 ^{1 C} n ¹ λ n ^λ n

+ 4

_e 2 HffH t 2

| A n | + —,— λ _n

^B . | + ^C . II — I    ■        ,

λ _n

^{| u} n ^{| C 2} | A n | ⁺ | B n | ⁺

² И I r= | C n| + λ_n

^{2 | A} n | +

1               3

—= | B n | + - | C n |

II—II t2eW2

+

. ^{2| a} n ^{| +} t dB n ^{| +} £^{|C n |}

+ [ 2 | A n | + —= | B n | + £ | C n |] t ²|| s||||—||e ²⁽ll^gll + l№ ²

t ²|| g'||e^{2||g|| t}2

where A n = A n - A n , Bl n = B n - B n , C n = C n - C n ,g = g - g. Indeed, the inequality (22) is stability estimate for the solution to the integral equation (12). The uniqueness of this solution follows from (22).

3.    The Local Existence and Uniqueness Theorem for the Inverse Problem

From (7) and taking into account conditions (4), we get the following equality:

M

h(t) = ^ u n ( t )sin \ ' A n x o , t G [0 ,T ] .

n =1

Substituting the right side (12) instead of u _n ( t ) in (24) and then differentiating four times, after simple transformations, we obtain an integral equation with respect to g(t) :

=    ' ^{h (IV} '

M

¹ V ¹

a" ^{( x} 0 ) n = A n + ¹

-

^{( A} n x/A n ^{( A} n ⁽ A n + B n ) + B n + ^C n ) ^sin y/^ nt ^sin y/^ n xo ⁽²⁵⁾

1               1

o^E A n+т [^( A n ⁺ C “ ^{) e} n =1

t + ^A 2 ^{( A} n ^v

1 a ‘‘ ( x o )

∞ ^t

^ An sin \Anxo   д(т) [un(t - т)+ Un(t - т)] dT n=1              0

tτ

1          An a‘‘(x ) £ A + 1 sin vAnxo   I g(v v s)un (s)Fnv (t v т) ds dr,

⁰ n =1 ⁿ                _{0 0}

where a ‘‘ ( x o ) = 0 .

We require the fulfillment of the following matching conditions

h (0) = a (0) ,    h'(0) = b (0) ,    h " (0) = c (0) .

Rewrite (26) in the form of the operator equation

g = ^Л g ^,

where Л is defined by the right side of equation (26):

^(Л g') ^{( t}') = g o ^{( t ) v}

1 a ‘‘ ( x o )

1 M a‘‘(xo)

n =1

λ n

^A n + ¹

∞t

^2 An sin y/Xnxo   д(т) [un(t v т) + Un(t v т)] dT n=1              0

tτ sin ^Anxo У У д(т v s)un(s)Fnv(t — т) ds dт,

where

'     = a      ^{h lV} '

1 a ‘‘ ( x o )

1 a ‘‘ ( x o )

∞ E n =1

∞

E n =1

^A n + ¹

( A n y/X n ( A n ( A n + B n ) + B n + C n ) sin y/An t sin ^A ^ x o

T-- [ ^A n ^{( A} n + C n ^{) e} t + ^A n ( A n ^A n + ¹ L

The main result of this work is the following theorem:

Theorem 2. Let the conditions of Theorem 1 are satisfied, besides a ( x ) G C 5 [0 , 1] , b ( x ) G C 4 [0 , 1] , c ( x ) G C 3 [0 , 1] , a ^IV (0) = a ^IV (1) = c ‘‘ (1) = 0 , a ‘‘ ( x o ) = 0 and matching condition (27) hold. Then there exists a number T * G (0 , T ] , such that there exists a unique solution g(t) G C [0 ,T * ] of the inverse problem (1) - (4) .

• <1 For simplicity, we denote

ao = llall c ⁵ [0 , 1],    bo = llbll c ⁴ [0 , 1],    co = llcll c ³ [0 , 1],    ho ^:= llhll c ⁴ [0 ,T ]•

We consider the functional space C [0 , T ] with the usual norm given by the relation ||gl| = max _{t e} [o ,T ] |g ( t ) | . Direct calculations show that we have the estimate

1Ы <

1 | a ‘‘ ( x o ) |

In the space C [0 ,T ] , by B ( g o , ||g o||) we denote the ball with the center g o and radius ||g o|| , i. e.

B ( g o , Ilg olD := { g ^{( t )} £ C ^{[0 ,T ]}: llg - g o II C ||g o II} -

The fact that the function g ( t ) belongs to the ball B(g o , | g o ||) implies the inequality

llgll C 2 | go | .

Let us show that Л is a contraction operator in the ball B(g o , | go||) provided that T is sufficiently small number.

Let us verify the first condition of a fixed point argument. After making obvious estimates from (29) based on (13), (14) and (30) for g ( t ) £ B(g o , | g o ||) , we get

^{| л} g - g o I ^C

1 ^M                t

——- ^ An sin VA^xo  g(T) [un(t - т) + un(t - т)] dT a (xo) n=i               o

+

1 a" ( x o )

M

E n=1

λ n

^A n + ¹

tτ sin ^Anxo У У g(T

— s ) u _n ( s ) F n ⁴⁾ ( t — т ) ds dT

C |a"(xo)| (ao + bo + ^^oI (t + t2e2Mt2 + t3||go||e2||g0^2) := |go|Kimi(t), where C is positive number, Ki = |a‘‘(X0)|(ao + bo + co). By T1 we denote the positive root of the following trancendent equation:

m i ( t ) =: t + t ² e ^{2|g o |t} 2 + t ³ | g o | e ^{2|g 0 ¥}2 .

Note that m 1 ( t ) is positive monotonically increasing function of t, and m 1 (0) = 0 . It follows that the equation m i ( t ) = K i have unique positive root. If we choose t £ (0 ,T i ] , then ^л g ^£ B ⁽ g o , IlgolD-

We now check the second condition of a fixed point argument. Further

+

Л — A g c

+

^{1 E A} a"( x o ) n = A n + 1

1    “           a„(xo) ^2 An sin VAnxo J (g(T)un(t — т) — д(т)un(t — т))d 0 n=1

1    “          az/(xo) 52 An sin VAnxo J (я(т)un(t — т) — д(т)u'n(t — т)) dт

0 n=1

t

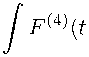
τ

τ

т — s ) — g ( s ) u _n ( т — s )) ds dт

^X | a" ( x o ) |

M

E (Ant (1 + Ant) |gun n=1

— gu n | + A n t | gu n — gu n| (

The integrands in the integral can be estimated as follows:

I gu n — gU n| = | ( u n — U n )g + U n (g — g ) I C 2 | g o | ||U n|| + | U nII Ill'll -

Thus, we get

л — A g| c K 2 [te ^{4||g o ||t} 2 + t ² e ^{8||g o ||t} 2 + t ³ | g o | e ^{8|g 0 ||t 2}] ЦЯ

where K2 = । ,,C   (ao + bo + co) • Therefore, if T2 is the positive root of the equation la'(x0)| te4lg0bt2 + t2e8||go||t2 + t3^   ||e8||go||t2 = 1

K 2

then for t G (0 , T 2 ] the operator Л contracts the distance between the elements g(t), g (t) G B(g o ; | g o | ) . Consequently, if we choose T * <  min { T i , T 2 } C T , then the operator Л is a contraction in the ball B ( g o ; | g o||) . However, in accordance with the Banach theorem [28], the operator Л has unique fixed point in the ball B(g o ; | g o ||), i. e., there exists a unique solution of equation (28). Theorem 2 is proven. >

4.    Conclusion

In this work, inverse problem was considered for determining the kernel g ( t ) included in the equation (1) by using additional condition (4) of the solution of problem with the initial and boundary conditions (2), (3). Sufficient conditions for given functions are obtained, under which the inverse problem has a unique solution for a sufficiently small interval. Interesting problems arise in the case when, simultaneously in addition to the convolution kernel g ( t ) , some of initial functions a ( x ) , b(x), c(x) in (2) is also to be determined. Then, it is clear that two additional conditions must be specified, so far such a problem is open.