Задача оптимального измерения с учетом резонансов: алгоритм программы и вычислительный эксперимент

Динамические измерения приобретают все большее распространение в технике и научных исследованиях. Изменение требований к результатам измерений является следствием выдвигаемых требований к качеству испытаний и эффективности производства. Так, одной из наиболее значимых в теории динамических измерений является проблема восстановления измеряемого сигнала. Отметим, что эта задача математически некорректна, поэтому для ее решения А.Л. Шестаковым и его учениками были предложены технически обоснованные гипотезы [1 – 3], решения которых были ≪ воплощены в металл ≫ . Затем А.Л. Шестаковым и Г.А. Свиридюком впервые для решения задачи восстановления динамически искаженого сигнала было предложено использовать методы теории оптимального управления [4], а полученную задачу называть задачей оптимального измерения . Полученная математическая модель – модель Шестакова-Свиридюка – позволила начать численные исследования задачи оптимального измерения [5, 6].

Однако искажение измеряемого сигнала часто случается не только из-за механической инерционности ИУ, но и в следствие механических же резонансов. В реальной ситуации в ИУ встраиваются фильтры, которые ≪ вырезают ≫ резонирующие частоты измеряемого сигнала. Иногда эти фильтры тоже резонируют, но уже на другие частоты, поэтому устанавливают дополнительные фильтры, которые устраняют возникшие резонансные частоты и т.д. В [7] А.Л. Шестаковым и Г.А. Свиридюком предложена модель оптимального измерения, где измерительное устройство обладает не только механической инерцией, но и резонансами. Итак, рассмотрим модель Шестакова – Свиридюка с учетом резонансов.

Пусть № = {x G L2((0,t), Rn : x 6 L2((0,t), Rn)} - пространство состояний, U = {u G L2((0,t), Rn) : u(p+1) G L2((0,t), Rn)} - пространство измерений и Y = C[№] - пространство наблюдений при некотором фиксированном т G R .. Выделим в U замкнутое и выпуклое подмножество U∂ – множество допустимых измерений. Требуется найти оптимальное измерение v G Ud почти всюду на (0,т), удовлетворяющую системе леонтьевского типа

Lx = Mx + Du(1)

y = Nx(2)

при начальных условиях Шоуолтера – Сидорова

[(^L - M)-1 L]p+1 (x(0) - xo) = O, минимизирующую значение функционала

• ^{1    T}ll                       112 P^{+1 T}

  J(v) = min J(u) = min u ∈ U ∂         u ∈ U ∂

  
  

E / | s“ ( t ) - y 0,q' t ) dt + E /(F q u ^{(q )}W,u ^(q) ( t»dt

. q=0 0q=

Здесь x = ( x i , X 2 ,..., x _n ) и X = ( X i ,X 2 ,...,X _n ) — вектор-функции состояния и скорости изменения состояния измерительного устройства соответственно; u = ( u i , U 2 ,..., u _n ) и У = (y 1 ,y ₂ ,... ,y n ) — вектор-функции измерений и наблюдений измерительного устройства соответственно; y 0 ( t ) = ( У 01 ( t ) , У 02 ( t ) , • • • , y 0n ( t )) — наблюдение, полученное в ходе натурного эксперимента; n – число параметров состояний системы; L и M – квадратные матрицы порядка n, представляющие собой взаимовлияние скоростей состояния и состояния измерительного устройства соответственно, D и N – квадратные матрицы порядка n, характеризующие взаимовлияние параметров измерения и связь между состоянием системы и наблюдением соответственно, u : [0 ,T ] ^ R ⁿ , F q G L ( U ) — самосопряженные положительно определенные операторы, q = 0 , 1 , ..., p +1 , || • || и (• , •) — евклидовы норма и скалярное произведение в R ⁿ соответственено.

Заметим, что системы леонтьевского типа являются конечномерным частным случаем уравнений соболевского типа . Поэтому, при изучении их мы будем использовать идеи, методы и результаты общей теории [8], адаптированные к конечномерной ситуации. В общем случае det L = 0 , матрица M - ( L, р ) -регулярна, т.е. существует число a G C такое, что det( aL — M ) = 0 , существует число p G { 0 } U N равное нулю, если в точке С5О L-резольвента ( ^L — M ) ^-1 матрицы M имеет устранимую особую точку; и равное порядку полюса в точке С5О матриц-функции ( ^L — M ) ^-1 в противном случае.

Несколько слов о начальном условии Шоуолтера-Сидорова (3), рассматривается оно при некоторых X 0 G R n , где a G p ^L (M ) = { д G C : det (^L — M ) = 0 } , R ^ (M ) = ( aL — M ) ^-1 L - правая L -резольвента матрицы M . В случае det L = 0 оно совпадает с начальным условием Коши. Однако использование условия Шоуолтера – Сидорова при численных исследованиях прикладных задач, сводящихся к системам леонтьевского типа или использующих их, позволяет снять ограничения на размер матриц, входящих в состав системы [9, 10]. При использовании начального условия Коши необходимо согласование начальных данных, проверка которых вызывает значительные трудности и накладывает ограничения при численном решении как начальных задач, так и задач оптимального управления. Кроме того, по мнению ряда авторов [11, 12], задача Шоуолтера – Сидорова более естественна для уравнений соболевского типа, чем задача Коши, наконец, укажем еще полезное обобщение [13] задачи Шоуолтера – Сидорова.

Функционал качества состоит из двух слагаемых, его минимизация позволяет находить такое оптимальное измерение, при котором 1) достигается наименьшее расхождение как значения выходного сигнала к выходному сигналу модели датчика, так и их производных,

• 2) нивелируется воздействие резонанса. Таким образом, второе слагаемое играет роль резонансных фильтров.

Для проведения вычислительных экспериментов авторами предлагается использовать следующий вид функционала качества:

1 T                      „                  в т

J ( u )= в £ / \ \ y ( ^q ) (t) - у <^) | | dt + (1 - в ) £ ( f . u^(t),u ( ^q\t)}dt,        (5)

q=0 О                                  q=0 0

где в E [0 , 1] и 1 — в — весовые коэффициенты двух целей функционала качества, вариация которых позволит оценить взаимосвязь точности измерений и нивелирования резонансов, 0 <  p +1 . Возможность использования величины 0 показана в [14].

Статья, кроме введения, содержит две части и список литературы, который не претендует на полноту, а отражает лишь вкусы и пристрастия авторов. В первой части статьи описан алгоритм программы нахождения решения задачи оптимального измерения с учетом резонанса, а во второй – представлены результаты вычислительного эксперимента.

• 1.    Алгоритм программы

Программа предназначена для нахождения решения задачи оптимального измерения с учетом резонансов, написана на языке C++ с использованием компилятора visual studio. Он является современным языком программирования, позволяющим удобно писать эффективные программы. Большинство известных компиляторов других языков значительно проигрывают в скорости выполнения программ известным компиляторам C++.

В основе программы лежат методы решения задач оптимального управления для систем леонтьевского типа с начальным условием Шоуолтера-Сидорова [9]. Прежде всего заметим, что по построению пространство U сепарабельно. Значит, существует последовательность {U1} конечномерных подпространств Ul С U монотонно исчерпывающих пространство U, м т.е. Ul С Ul+1 и U Ul плотно в U. Поэтому ulk = ulk(t) будем искать среди векторов вида

1=1

l

l

l

u^l = col    £ a ji sin jt, £ a j ₂ sin jt, ..., £ a jn sin jt ,

j =0

j =0

j =0

где l E N , l > p . Для простоты алгоритм излагается в предположении о том, что существует точно одна частота ω , при которой измерительное устройство (ИУ) резонирует (заметим, что как алгоритм, так и программа позволяют рассматривать несколько частот). Пусть амплитуда резонанса ИУ равна A ω (амплитуда A ω снимается с реального ИУ, поэтому считаем A w E (0 , +^о)). Теперь построим одно из слагаемых функционала J из формулы (5)

( F o u^l,u^l ) = ( col I £ a ji sin jt + A w a wi sin wt,

\ j=0 j =w

£ a j2 sin jt + А _ш a w2 sin wt, ..., £ a j_n sin jt + A w a wn sin wt I , u^l ) .

j =0                                        j =0                                  I

• j = w                              j = w

Опишем логическую структуру программы. В ее состав входят следующие модули: – ввод данных;

– расчет решения;

– операции над матрицами.

Для представления чисел используется вещественный тип двойной точности (double). Для величин такого типа под порядок и мантиссу отвводится 11 и 52 разряда соответственно, длина мантиссы определяет точность числа, а длина порядка – его диапазон.

Ввод данных осуществляется из конфигурационного текстового файла, задающего параметры расчета и имена файлов, из которых загружаются необходимые массивы. В качестве входных являются следующие данные:

• –    индекс выбранной задачи управления, т.е. определяется вид функционала качества, который будет принят для рассчета;

• –    имена файлов, в которых записаны массивы, входящие в состав системы и функционала качества - матрицы L , M , B , C , F q , q = 1 , 2 , ...,p + 1 , размера n х n , матрицы коэффициентов тригонометрических многочленов u ( t ) , число строк которых равно числу компонент n, а число столбцов равно l + 1 , массив данных наблюдения Y 0 , массив X q начальных значений состояния системы, значения амплитуды резонанса A ω и частоты резонанса ω ;

• –    значения параметров расчета – минимальный h _mi_n и максимальный h _max шаги изменения элементов матрицы (a ij ) вектор-многочленов u^l(t) , r — коэффициент изменения шага;

• – константы β – весовой коэффициент в функционале качества задачи оптимального управления, τ – правая граница отрезка, на котором рассматривается задача, η – порядок квадратурной формулы Гаусса, θ – параметр второго слагаемого функционала качества, d – радиус шара в пространстве R ^l+1 , взятый в качестве U ^l _∂ .

На рис. 1 представлена обобщенная схема алгоритма решения.

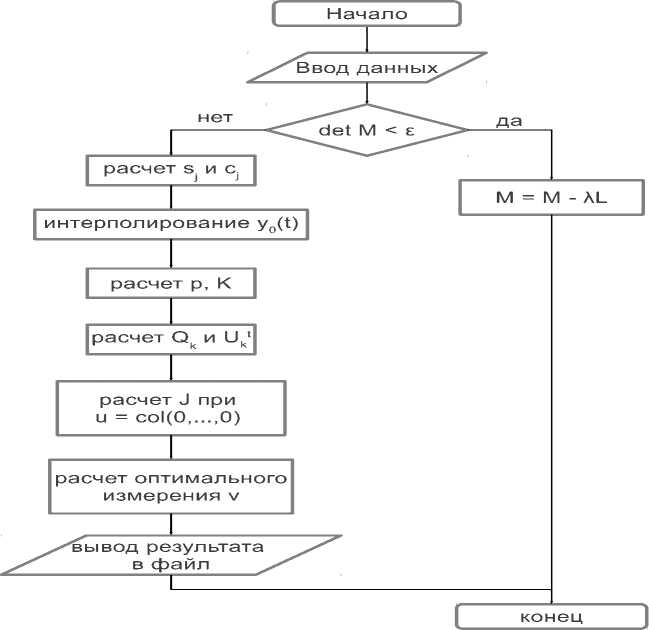
Рис. 1. Обобщенная схема алгоритма расчета решения задачи оптимального измерения

В схеме расчет s j и ω j представляет собой обращение к библиотеке класса С++ для расчета узлов и весов квадратурной формулы Гаусса.

При интерполировании y o ( t ) использован метод Лагранжа.

Приближенное значение состояния измерительного устройства, в предположении (L,p)-регулярности матрицы M и det M = 0, находится по формуле p                           m ττ

τ

2 s j ' △ c j ,

Xk(t)=£HM-1(In-Qk) (Duk)(q)(t)+Ukxo + 2£r| — 2sjQkDuk(T + q=0                                         j=0

где S j и C j - узлы и веса квадратурной формулы Гаусса соответственно, S j € [0 , T ] , j = 0 , m, m + 1 - количество узлов, H k = M ^—1 (Q k - I n ) L — нильпотентная матрица со степенью нильпотентности p ,

/ /         t        \ —1 \ k⁽ p ⁺¹⁾

° k=( (l - _k. ■ M) l)     • Qk = ^M¹ )) ^p+1 -

// т т X -1 \^k (P ⁺¹ )^-V     т т X -1

R —2sj = L-~sm} L) L- -      m} k y\   k(p +1) / J \   k(p + 1) J причем k = max {k1, k2}, где

n k1 > - £ |ai| + 1, l=q+1

t € [0 , т ] , a >  max

1q - k2 > |aq| (n - q)n-q Ц0 ।al । (n - q + 1Г l + 1, Itl < 1

{1,Ы-1 (£Ja^L

Далее при условии, что все коэффициенты тригонометрических многочленов в (6) равны нулю, т.е. u = col(0,..., 0), находятся значения вектор-функций состояния измерительного устройства x в каждой из m + 1 точек, затем вычисляются соответствующие им значения у и, наконец, значение J при найденном y и начальном u. Процедура оптимизации подробно представлена на рис. 2. Отметим используемые в блок-схеме обозначения:

о a - матрица коэффициентов многочленов из (6), используемая в начале циклов;

о A - матрица, аналогичная а , создаваемая для промежуточных расчетов внутри циклов;

о A j - матрица, аналогичная а , для элементов которой в цикле достигается минимум функционала при изменении коэффициента с индексами (i,j ) ;

о A ik - матрица, аналогичная а , для элементов которой в строке i достигается наименьшее значение функционала, при этом фиксируется номер столбца k в этой строке;

о J ( A ) , J ( а ) - значения функционала при коэффициентах полиномов из (6), образующих соответственно матрицы A и a ;

о h _max , h min , А - максимальный, минимальный и промежуточные шаги оптимизации.

В результате реализации процедуры оптимизации определяется значение измеряемого сигнала v и значение функционала J .

При создании программы были использованы методы оптимизации кода и вычислений. Для упрощения написания программного кода была использована такая возможность языка программирования С++ как перегрузка операций. Создав класс с собственным типом

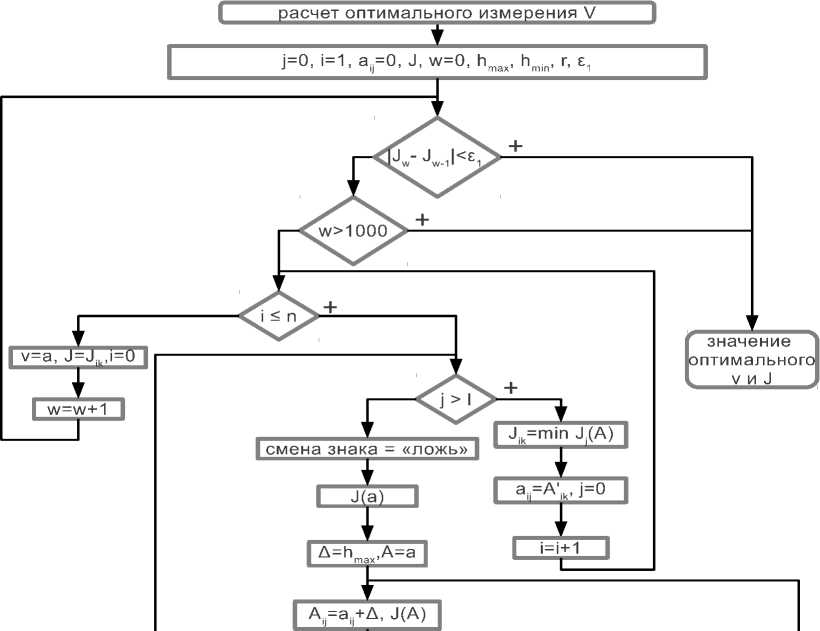
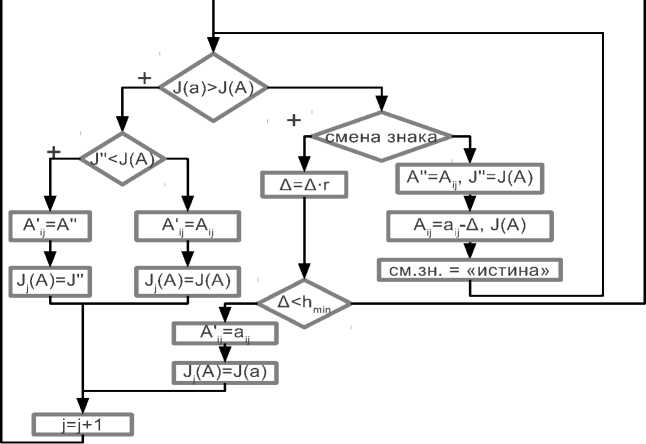
Рис. 2. Блок-схема процедуры оптимизации данных, по сути содержащий в себе двумерный массив как представление матрицы, получили возможность скрыть в классе реализацию математических операций над матрицами. Таким образом формулы расчета в тексте программы выглядят наиболее естественно, что сказывается на понимании программного кода и легкости его модификации.

Так же программа была подвергнута оптимизации скорости вычислений. Вследствие того, что при вычислении многих процедур программы значения функции необходимо получать не для бесконечного количества значений переменных, а в основном только для узлов интегрирования, то с учетом максимум двойного интеграла в формуле функционала качества достаточно сохранить для m ² количества значений, где m + 1 количество узлов интегрирования. При выборе даже 101 точки получаем порядка 10000 значений, умножив которое на 8 байтовое представление числа, получим около 80 Кбайт на один кэш. В основной процедуре рассчитываются до 20 функций, максимальный кэш для функции интегрирования составляет 212 Мбайт, а суммарный кэш примерно составляет 0,5 Гбайт оперативной памяти. При современном оснащении компьютеров такой расход памяти и является допустимым, а в то же время позволяет на порядок повысить производительность расчетов. Для реализации кэша в языке С++ была использована возможность статического объявления переменных, когда они размещаются не в стеке, а в отдельно выделенной для нее памяти, и доступна на все время выполнения программы.

Программа эксплуатируется на персональном компьютере платформы Intel ( 80 х 86 ), работает под управлением Microsoft Windows. Вывод результатов расчета осуществляется в текстовый файл. Кроме того в ходе работы программы выводится подробный протокол расчета.

2. Вычислительный эксперимент

В качестве примера рассмотрим модель датчика, передаточная функция которого имеет вид

_W              80000000000

^{W d ( p ) =} ( p ² + 140 p + 10000) ( p + 200) ^{3 .}

Тогда, модель измерительного устройства будет представлена системой

/ о          1           о х =      0         0           1 х + (0 02 • 106) и,(1)

\-2 • 10 6 - 3 , 8 • 10 4 - 3 , 4 • 102/

У = (1 0 0) х,(2)

причем в начальный момент времени вектор-функция состояния измерительного устройства равна нулю.

Представим систему (3.1)-(3.2) в виде системы уравнений (1.1)-(1.2), построив матрицы L , M , N и D следующим образом

/ 1 0 0 \             / L = 0 1 0 , M = 001        - / 1 0 0 \ N = 0 0 0 , 000 Кроме того, пусть известна частота ω = Реализовав первый шаг алгоритма при l

0           1            0      \ 0             0              1 , 2 • 10 6 - 3 , 8 • 10 4 - 3 , 4 • 102/ / 0  0    0 \ D =  0  0    0     . У0  0  2 • 106/ 4000 и амплитуда A = 0 . 03 резонанса. = 31 , получили p = 0 , K = 88796 .

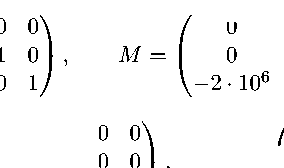
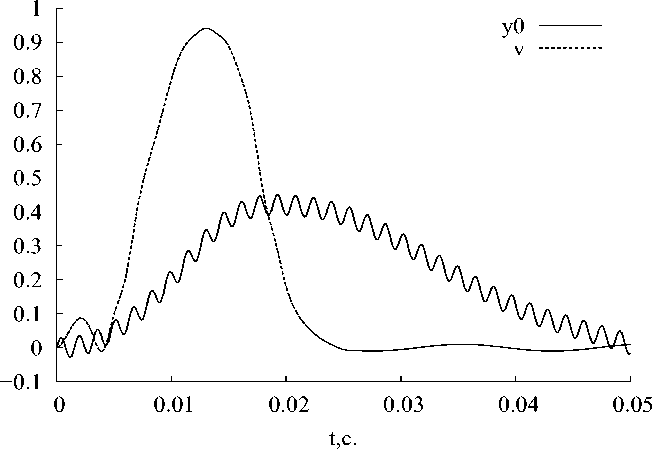
Рис. 3. Восстановленный сигнал v = v ( t ) и значения наблюдения y ₀ = y o ( t )

Построим множество U ^l _∂ . Вектор измерений u полностью определяется своей третей компонентой, следовательно, для его нахождения можно ограничиться пространством R l ⁺¹ . Пусть, далее, имеется информация, что значения измеряемого сигнала не превосходят 2, поэтому в качестве U d можно взять замкнутый шар в пространстве R l ⁺¹ радиуса 2 с центром в начале координат. График функции восстановленного сигнала и значения выходного сигнала, полученного в результате натурного эксперимента, представлены на рис. 3.

Различия представленных графиков отражают инерционность измерительного устройства, проявляющуюся в сглаживании ≪ пикообразного ≫ сигнала и запаздывании выходного сигнала датчика.