Задача оптимального распределения ресурса между составляющими центра обслуживания вызовов

Индустрия центров обслуживания вызовов (ЦОВ) или контакт-центров, являющихся эффективным инструментом взаимодействия компаний с клиентами, развивается стремительно как по производительности, так и по экономическим показателям [1-2]. Несмотря на широкий размах отрасли за рубежом, где доходы от использования ЦОВ исчисляются миллиардами долларов, в России многие компании, взаимодействующие с большим числом клиентов, не имеют собственных ЦОВ, опасаясь больших расходов на их содержание [3].

Оптимальным решением в этой ситуации является аутсорсинг ЦОВ, т.е. аренда на определенный период некоторых из его функций [4]. При этом возникает задача оперативного расчета количества арендуемых каналов связи, числа операторов, обрабатывающих заявки клиентов, и номенклатуры технического персонала, удовлетворяющих заявки по устранению возникших проблемных ситуаций, с учетом выделяемых финансовых ресурсов на аренду ЦОВ. Решение данной задачи сводится к максимизации прибыли от использования ЦОВ, косвенным показателем которой выступает вероятность удовлетворения заявок клиентов.

Несмотря на неоднородность структуры ЦОВ для расчета показателей их функционирования использовались простейшие аналитические модели, построенные на базе формул Эрланга [5-6]. Однако применение в качестве целевых функций известных моделей ЦОВ в виде однофазных систем массового обслуживания (СМО) затрудняет решение задачи. Поэтому необходи-

мо рассмотреть ЦОВ как сложную систему, состоящую из трех подсистем: канальной (КПс), операторской (ОПс) и технической (ТПс). Учитывая последовательность прохождения и обработки заявок клиентов через указанные подсистемы, моделью ЦОВ является трехфазная СМО с различными частными моделями на каждом этапе обслуживания.

Модель канальной подсистемы ЦОВ

Канальная подсистема ЦОВ содержит n ка-

налов связи, за которыми закреплен один телефонный номер дозвона в клиент-центр. Предполагается, что звонки абонентов равномерно

распределены на исследуемом интервале времени T (свойство стационарности потока заявок) и вероятность появления двух и более звонков

в один и тот же момент времени ничтожно мала (свойство ординарности). Если к тому же интенсивность звонков в будущем не зависит от их ко-

личества в прошлом, то их можно рассматривать как простейший поток заявок λ ₁ , а функционирование КПс исследовать с помощью Марковс-

ких процессов.

Каждый поступивший звонок переводит

КПс из j -го состояния S

(1) j

в состояние

S

где j = 0, 1, 2,..., n , при этом состояние S

j+ 1

со-

ответствует случаю незанятости всех каналов,

состояние S ^{( 1 )}

– занятости одного канала (ос-

тальные свободные) и т.д., а состояние

S П¹ ) - за-

нятости всех каналов. Среднее время занятости

канала τ ₁ определяет интенсивность обслуживания заявки в первой системе μ ₁ = 1 τ ₁ . Так как при занятости всех каналов заявка на обслужи-

вание не принимается, то моделью первой подсистемы ЦОВ является n -канальная СМО с отка-

зами, для которой вероятность отказа заявки на обслуживание определяется по первой формуле Эрланга [7]:

p .

отк 1

n

= (щ Unn!) Z (i lux )4j!. ,

n

j=0

Вероятность того, что заявка будет обслужена (относительная пропускная способность КПс) определяется из выражения (1) [7, 8]:

^q1 = ¹ - Р отк 1 = ¹

-

( i n ₅ ni ) . £( i/^ y/j ! . (2)

j =0

Модель операторской подсистемы ЦОВ

Если в течение заданного времени T на вход КПспоступило N заявок,то на выходе первойпод-системы будет N • q i = M заявок. Следовательно, интенсивность обработанных заявок, поступающих на операторную подсистему ЦОВ:

2 2 = M/T = q 1 N/T = 2 1 • q 1 .

Так как значение τ об значительно больше, чем в предыдущих подсистемах, то заявки покидают систему с интенсивностью v = 1Тдоп ,, где Тдоп -математическое ожидание допустимого времени пребывания заявки в системе, являющееся случайной величиной τ доп с экспоненциальной плотностью вероятности. Уходы заявок возможны либо из очереди, если время ожидания tож > тдоп, либо из канала обслуживания, если tож < тдоп, что отражается в двух потоках уходов с интенсивностями соответственно vож и vоб .Таким образом, в ТПс потери заявок возможны либо в форме отказа вследствие переполнения СМО, либо в фор-

Интенсивность обслуживания заявки оператором ^ 2 , при этом, как правило, число операторов m гораздо меньше числа обслуживаемых каналов связи n , но даже при занятости всех операторов (состояние S j² второй подсистемы) «необслу-женные» каналы дожидаются своей очереди. В этом случае моделью ОПс является m -канальная СМО с ограниченной очередью, для которой относительная пропускная способность [7]

ме ухода нетерпеливых заявок из системы.

Вероятность отказа Р_{отк 3} определяется как ве-

роятность нахождения системы в состоянии

S

k+r

[8]. Тогда вероятность обслуживания заявки в

ТПс:

q 3 = 1 - Р отк З = 1 - p k + r = 1

^^^^^^в

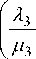
q 2 = 1 -

n

^2 I ( 2 ) n-m । ⎜ ² ⎟ ⋅ p m ^{n m} m ⎜_{⎝μ 2} ⎟_⎠ 0

x^ k !

k

1+^1

⎜_{⎝     μ 3} ⎟_⎠

r

■ П“

1 =1 L v

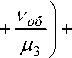
lν ож

л -1

μ ₃

где вероятность отсутствия заявок в ТПс [8]:

где предельная вероятность состояния отсутствия заявок во второй подсистеме

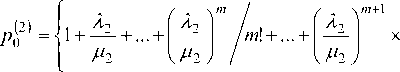
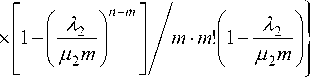
Модель технической подсистемы ЦОВ

После уяснения содержания заявки абонента оператор делает запрос в техническую подсистему, соответствующую уровню выполнения заявки. Интенсивность поступления заявок в ТПс:

1 з = q 2 ^ 2 = q^ i • (5)

Частной моделью ТПс является СМО,содержа-щая k однотипных каналов обслуживания (технических работников одинаковой квалификации) и характеризующаяся экспоненциальным временем обслуживания со средним значением т ^ или, что эк-вивалентно,с простейшим потоком обслуживания с интенсивностью ^ 3 = 1 т_ы , независимо от типа обслуживаемой заявки.Дисциплины ожидания в очереди длиной r и обслуживания – бесприоритетные.

k

P 0^{3 )} -| 1 + z-

I i =1

rl

^zn l=1 i=1

(^з /^з ) i    +    ⁽Л /^з ) k     _х

4^{1 + V} об /^ 3 ) i    ^{k! ( 1 + v} об /^ 3 ^{) k}

1 -1

^3 /^             .

^{+ v} об/^ 3 ) ^{+ iv} ож /^ 3 ^] "

Формулировка задачи распределения ресурса в ЦОВ

Заявки клиентов будут полностью обслужены в ЦОВ, то есть произойдет событие А , если они будут обслужены во всех подсистемах, что соответствует событиям А 1 , А 2 и А ₃ с соответствующими вероятностями q i , q 2 и q 3 . Известно [9], что вероятность произведения нескольких событий

Р ( А ) = Р ( А 1 А 2 А з ) = Р ( А 1 )• Р ( А 21 А 1 )• Р ( А з | А 1 А 2 ) , где p ( A d | A 1 ... • A d -1 ) - вероятность события A d при условии, что все предыдущие события имели место. Данные условные вероятности легко получить при выражении интенсивностей входных заявок в ОПс и ТПс с учетом зависимостей (3) и (5). Тогда полная вероятность обслуживания заявки в ЦОВ Р обсл = Р ( А ) :

^Р обсл = q i ( ^ 1 , n )- q 2 ( ^ i q i , m )- q 3 ( ^ i q i q 2 , k ) •    (7)

При этом каждый из частных показателей оп- ределяется по соответствующим моделям СМО вида (2), (4) и (6) и имеет прямую зависимость от количества обслуживающих элементов (ОЭ) – каналов n, операторов т и техников k. Однако рост количества ЭО ограничен суммарным ресурсом n

С ₂ , выделяемым на аренду каналов связи ^ c j ’ m                    j =1

оплату труда операторов ∑ c b и технического

k персонала ^cl ■ l =1

b=1

Обозначим числом xd количество обслужи- вающих элементов в d-ой подсистеме ЦОВ (в данном случае d = 1, 3); qd (xd) - вероятность обслуживания заявки в d-ой подсистеме; nd (xd)

– стоимость ОЭ в количестве xd в d-й подсис- теме. Полученные при расчете в соответствии с моделями (2), (4) и (6) данные, содержащие сведения о показателях обслуживания заявок q d и стоимостях подсистем cd, заносятся в таблицу 1, где Λ – некоторое число дискретных значений распределяемых ресурсов (причем n, m, k≤ Λ).

Таблица 1. Вероятности обслуживания заявок q_d и стоимости c_d подсистем ЦОВ при различных количествах ОЭ x_d

xd	Подсистема ЦОВ
	КПс (d=1)		ОПс (d=2)		ТПс (d=3)
1	9 1 ( 1 )	П 1 ( 1 )	q 2 ( 1 )	« 2 ( 1 )	q 3 ( 1 )	« 3 ( 1 )
2	q i ( 2 )	« 1 ( 2 )	q 2 ( 2 )	« 2 ( 2 )	q 3 ( 2 )	« 3 ( 2 )
Λ	q 1 ( Л )	« 1 ( Л )	q 2 ( л )	« 2 ( Л )	q 3 ( л )	« 3 (л)

Задача распределения ресурса между подсистемами ЦОВ формулируется следующим образом: требуется найти вектор параметров *      *    *    *

X = ( x 1 , Х 2 , Х 3 ) такой, что показатель ЦОВ

Р обсл = q i ( x i ) • q 2 ( x ) • q 3 ^{( x} 3 ) ^ max       ⁽⁸⁾

при условии, что

⎛ n m k ⎞ ^⎜ ∑ c j + ∑ c b + ∑ c k ^⎟ I j = 1 b = 1 l = 1 )

^ C ^ .

Решение задачи методомдинамического программирования

Учитывая мультипликативность целевой функции (8), решим оптимизационную задачу с помощью метода динамического программиро- вания, используя процедуру обратной прогонки (начиная с последней подсистемы — ТПс) [7]. При этом d                            d теме, состояние zd выражает суммарные затраты на содержание обслуживающих элементов подсистем с номерами d, d + 1,..., п (в рассматриваемом частном случае π = 3), а вариант решений xd представляет собой число ОЭ в d-й подсистеме.

Обозначим f _d максимальное значение вероятности обслуживания заявки в цепочке из последовательного соединения подсистем с номерами d , d + 1,..., п при заданной стоимости ОЭ. Тогда рекуррентное соотношение, связывающее f _d для значений индекса d , может быть представлено в виде:

f n ⁽ z n ) =    max ^{{ q} n ^{( x} n ^{)} ;} "■;

xπ cn (xn )— zn                        (9)

f d ( z d ) = max ^{ q a ( x d ) • f d + 1 [ z d - c d ( x d )]} .

xd cd (xd ^ zd

Промежуточные результаты расчета для d-го шага заносятся в таблицу 2, где значения условного выигрыша f d (zd) определяются в соответствии с выражением (9) для каждой строки при распределении ресурса в количестве zd, а условное оптимальное решение xd (zd)=arg max{qd (xd) •f d+1 [zd - cd (xd)]}. xd

Таблица 2. Форма представления результатов промежуточных расчетов условных (по ресурсу) оптимальных параметров на d -ом шаге динамического программирования

zd	qd ( xd ) х х fd + i [ zd - cd ( xd ) ]			f d ( z d )	x d ( z d )
	х=1		х=Λ
z d min
z d max

При этом для п -го шага величина f _{d + 1} = 1 , а для первого шага переменная z 1 соответствует величине ресурса, распределяемого между всеми подсистемами, то есть z 1 = C ^ .

Для решения задачи необходимо предварительно определить границы зна чен ий каждой из переменных состояния Z d , d = 1, п .

Для третьего шага наименьшее значение Z3min = С3 (хз = 1) равно затратам на содержание одного техника. Наибольшее значение z3 выбирается из условия обеспеченной работоспособности центра обслуживания вызовов при минимальном числе элементов в первой и второй подсистеме (то есть при xi = 1, Х2 = 1). При этом Z3max = CS - [ci (Х1 = 1)+ С2 ^2 = 1)], ГДе cl (x1 = 1) и c2 (x2 = 1) — затраты на аренду одного канала связи и заработную плату одному оператору.

Переменная z ₂ представляет собой часть ресурса, который должен быть распределен между второй и третьей подсистемами. Поэтому z _{2 m}in = С 2 ( x 2 = 1 ) + С 3 ( х з = 1 ) ■ Максимальное значение ресурса, которое может быть выделено для второй и третьей подсистем, определяется минимальными затратами на первую подсистему:

^z 2max = C S “ c l ^{( x} 1 = 1 ) ■

Значение условного выигрыша на первом шаге (в первой подсистеме – КПс) определяет искомое решение (8), то есть f 1 ( C _x ) = max Р обсл , а также оптимальное число каналов в КПс: x * ( C _z ) = n . Значения остальных составляющих искомого вектора X * = ( x * , x * , x * ) определяются на этапе прямой прогонки, который разворачивается в последовательности, обратной первому этапу (9), используя готовые рекомендации, представленные в таблицах вида 2 для различных шагов предварительного расчета.

Выводы

Центр обслуживания вызовов представляет собой сложную систему, состоящую из последовательно соединенных канальной, операторской и технической подсистем, поэтому для ее моделирования целесообразно использовать многофазную СМО. Частными моделями составляющих ЦОВ являются: для КПс – n -канальная СМО с отказами; для ОПс – т -канальная СМО с ограниченной очередью; для ТПс – k -канальная СМО с ограниченным временем ожидания.

Определение числа обслуживающих элементов в подсистемах ЦОВ (соответственно n , т и k )

осуществляется при решении оптимизационной задачи распределения ограниченного ресурса, а целевой функцией является максимизация произведения условных вероятностей обслуживания заявки в подсистемах центра.

Использование метода динамического программирования предполагает дискретизацию распределяемого ресурса С _Σ , число градаций которого зависит отстоимостиединицы ОЭвкаждойподсистеме и влияет на объем вычислительных операций на первом этапе решения задачи оптимизации.