Задача отсечения и произвольное выпуклое окно

сто обобщением задачи с треугольным окном.

Для определения принадлежности некоторой точки (x0,y0) внутренней области треугольника с вершинами A(x1,y1), B(x2,y2) и C(x3,y3) воспользуемся следующим кодом:

ВЕСТНИК Мордовского университета | 2014 | № 1-2

Задача о выпуклом окне известна, и подходы к ее решению упоминаются во многих публикациях [1; 3-5]. Если использовать идею с кодами, которые вычисляются для случая «правильного» четырехугольного окна [2], то задача о выпуклом окне окажется про- function Znak(xx1,yy1,xx2,yy2,x,y: real): integer;

var f : real;

begin

f:=(yy2-yy1)*x+(xx1-xx2)*y +(xx2*yy1-xx1*yy2);

if abs(f) < 1e-6 then Znak := 0

else if f < 0 then Znak := -1 else Znak := 1

end;

Построим код для некоторой тельно заданного треугольника точки (x0,y0) плоскости относи- (m=3):

function KOD (x0,y0: real) : string;

var i : integer;

v : string;

begin v : = ‘’;

for i : = 1 to m-1 do case Znak (fig [i]. x, fig [i]. y, fig [i+1]. x, fig [i+1]. y, x0, y0) of

• -1: v : = v+’-’;

• 0: v : = v+’0’;

• 1:    v : = v+’+’

end;

case Znak (fig [1]. x, fig [1]. y, fig [m]. x, fig [m]. y, x0, y0) of

• -1: v : = v+’-’;

• 0: v : = v+’0’;

• 1:    v : = v+’+’

end;

result : = v end;

Серия «Естественные и технические науки»

Визуализируем некоторую точку (x0, y0) на плоскости относительно заданного треугольного окна. Символьное представление кода показано на рис. 1. Обозначим такой код через КОД (x0, y0). Заметим, что на основе этого кода возможно построение его числового аналога. Полученный код далее можно использовать для определения принадлежности некоторой точки плоскости внутренней области заданного треугольника.

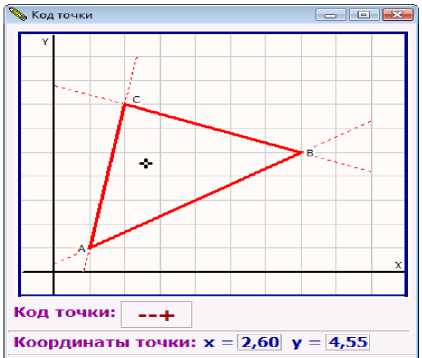
Рис. 1. Символьный код точки

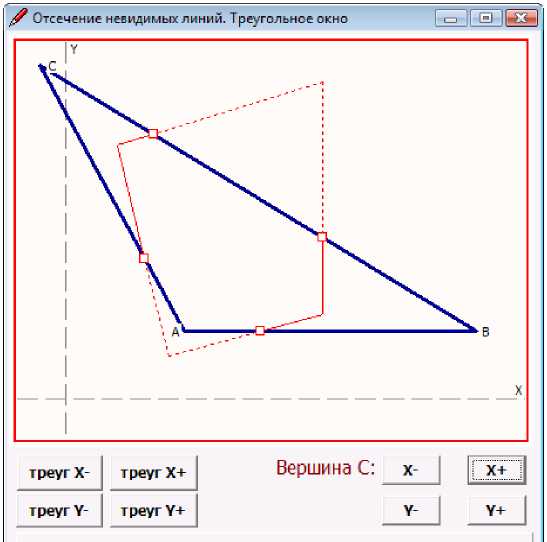
Р и с . 2. Результат работы компьютерной программы, треугольное окно

С целью выявления и устранения возможных ошибок в создаваемой программе необходимо проделать следующие действия: вывести только видимые части сторон произвольной плоской фигуры относительно треугольного окна (рис. 3); вывести только невидимые части сторон произвольной плоской фигуры относительно треугольного окна (рис. 4).

ВЕСТНИК Мордовского университета | 2014 | № 1-2

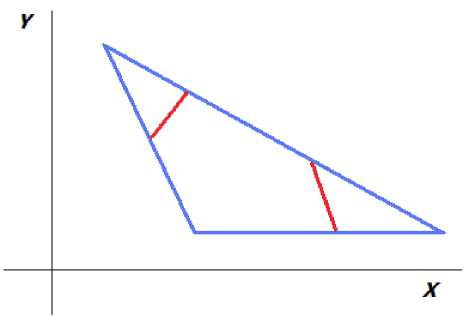
Р и с . 3. Отображение видимых линий

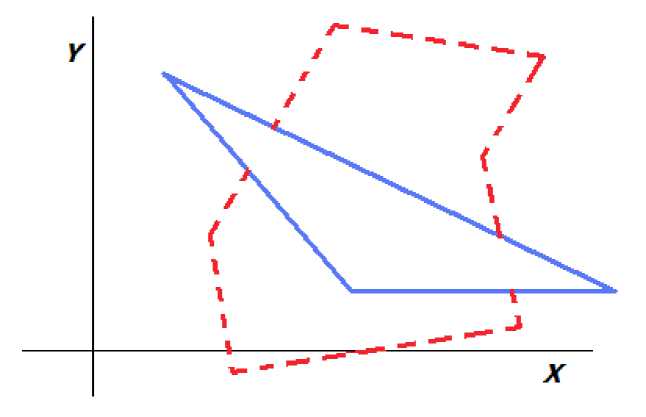
Р и с . 4. Отображение невидимых линий

Серия «Естественные и технические науки»

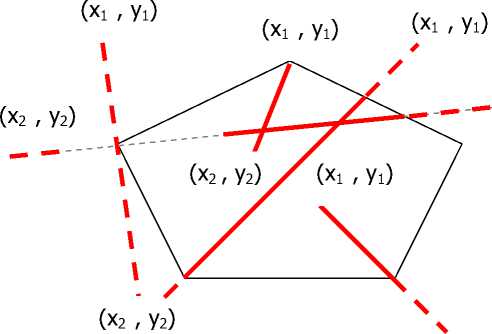
С точки зрения алгоритмизации, в рамках данной задачи нет проблем с переходом от треугольного окна к произвольному выпуклому окну. При рассмотрении произвольного выпуклого окна выделим ряд ситуаций, показанных на рис. 5–8. На первом из них не- которая вершина выпуклого окна лежит на прямой, образованной одной из сторон (x1,y1)-(x2,y2) произвольной фигуры. Назовем эти случаи ситуациями «одного нуля». Для их обработки достаточно проанализировать коды КОД(x1,y1) и КОД(x2,y2). 1 1

(Х1 , У1)

(xi , У1)

(X2 , У2)

Р и с . 5. Ситуации «одного нуля»

На рис. 6 показаны случаи 1–4, когда на прямой линии, определяемой стороной (x1,y1)-(x2,y2) произвольной фигуры, лежат две соседние вершины заданного выпуклого окна. По аналогии эти случаи назовем ситуациями

«двух соседних нулей». Для выявления этих ситуаций достаточно обращения к функции ZNAK(x1,y1,x2,y2,Fx,Fy), где (Fx,Fy) – одна из двух соседних вершин заданного выпуклого окна, лежащих на указанной прямой.

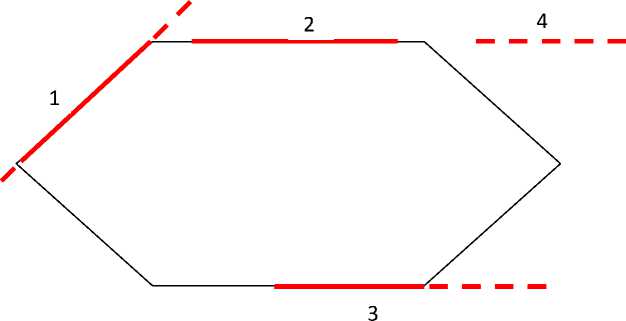
Р ис . 6. Ситуации «двух соседних нулей»

На рис. 7 показаны случаи 1–4, когда на прямой линии, определяемой стороной (x1,y1)-(x2,y2) произвольной фигуры, лежат две не соседние вершины заданного выпуклого окна. Эти случаи назовем ситуациями «двух несоседних нулей». Для выявления этих ситуаций вновь достаточно обращения к функции ZNAK(x1,y1,x2,y2,Fx,Fy), где (Fx,Fy) – одна из двух несоседних вершин заданного выпуклого окна, лежащих на указанной прямой.

ВЕСТНИК Мордовского университета | 2014 | № 1-2

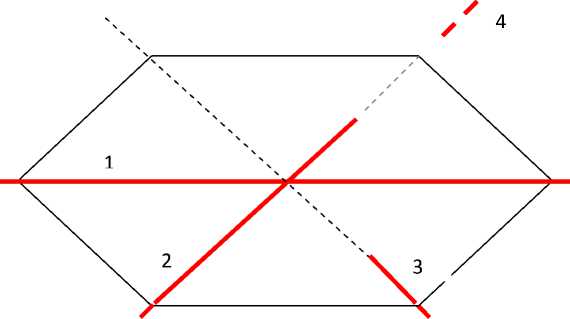
Р и с . 7. Ситуации «двух несоседних нулей»

фигуры, не лежат вершины заданного выпуклого окна. Эти случаи объединим в ситуации «ноль нулей».

Рис. 8 иллюстрирует случаи 1–5, когда на прямой линии, определяемой стороной (x1,y1)-(x2,y2) произвольной

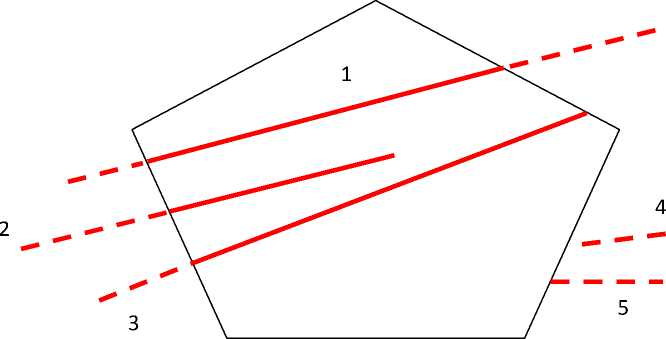
Р и с . 8. Ситуации «ноль нулей»

Серия «Естественные и технические науки»

В итоге получаются четыре незави- работы программы в случае произвольно-симые алгоритмические ветви. Результат го выпуклого окна представлен на рис. 9.

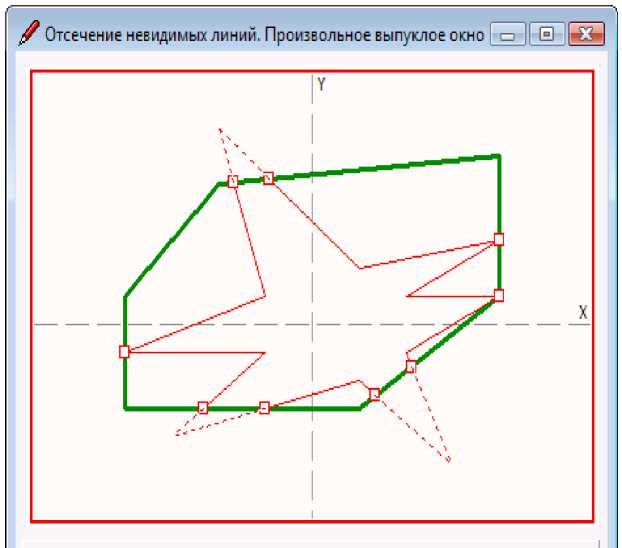
Р и с . 8. Произвольное выпуклое окно