Задача потери устойчивости тонкостенных конструкций из композиционных материалов, свойства которых зависят от типа нагружения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2019PNRPU MECHANICS BULLETIN

Использование композиционных материалов позволяет снизить вес тонкостенной конструкции, но затрудняет выбор надежных методов для прогнозирования потери устойчивости и моделирования при дальнейшем деформировании после локальной потери устойчивости [1–11]. Одной из проблем является корректный выбор свойств композиционного материала для расчетов, упругие характеристики которого зависят от типа нагружения. Например, разница в модуле Юнга при одноосном растяжении и сжатии у некоторых слоистых композитов может достигать 30–40 % [12]. Модели разномодульных материалов разрабатываются уже в течение длительного времени [12–18], однако в современных расчетных комплексах (ANSYS, ABAQUS и др.) их численная реализация для практического применения до сих пор отсутствует. Возможной причиной этого является необходимость проверки обеспечения в моделях фундаментальных принципов (выпуклость упругого потенциала, единственность решения), что в противном случае приводит к проблемам сходимости при численной реализации [19–20]. Кроме того, требуется постановка определенных дополнительных экспериментов для подбора параметров модели. На практике анализ потери устойчивости обычно предполагает сжатие конструкции, и выбор модулей упругости, полученных в испытаниях на сжатие, приводит к более точным результатам, но не гарантирует хорошей корреляции с экспериментами в случае анализа закритического поведения из-за игнорирования некоторых областей с преобладающим состоянием растяжения. Другим важным эффектом является нелинейность диаграммы при сдвиговом нагружении [21–24]. Учесть восприимчивость к виду НДС возможно при использовании моделей материалов, учитывающих изменение жесткости в зависимости от типа нагружения. Дальнейшим развитием нелинейно-упругой модели в задачах, связанных с анализом потери устойчивости и последующим деформированием вплоть до разрушения, является внедрение модели деградации жесткости композиционного материала, учитывающей снижение свойств материала вследствие повреждения в сочетании с нелинейной упругостью [28–29].

Определяющие соотношения, представленные в этой работе, основаны на использовании параметра трехосности, который характеризует напряженное состояние в материале [25–27]. Основными целями данной работы являются внедрение нелинейно-упругой модели в программное обеспечение МКЭ, тестирование ее на инженерных задачах устойчивости тонкостенных композитных конструкций и сравнение полученных результатов с моделью линейной упругости. Предлагаемый подход отличается от традиционной постановки задачи об устойчивости конструкции и заключается в численном решении задачи определения напряженно- деформированного состояния материала конструкции при продолжении деформирования в закритическом состоянии в прямой динамической постановке с учетом всех инерциальных сил. Отметим также, что рассматриваемые задачи подразумевают геометрическую нелинейность, в том числе с использованием линейно -упругого материала. Поэтому вне зависимости от учета геометрической нелинейности в дальнейшем использование модели линейно-упругого материала будем сокращенно называть линейной моделью.

1.    Модель анизотропной упругости с учетом нелинейности при сдвиговых нагрузках и зависимостью от вида нагружения

Рассматривается модель нелинейной упругости, предложенная в работе [25], основанная на использовании параметра вида напряженного состояния (или параметра трехосности) Е :

е о / Сто, где а - среднее напряжение, о = 1 / 3о„; о0 - интенсивность напряжений, о0 = ^(3/2) Sy Sy ; Sy — девиатор напряжений, Sy = о у - об-2.

Для учета нелинейности под действием сдвига вводится параметр Q в виде

Q = D y ^о у ,                    ⁽¹⁾

где компоненты тензора D имеют следующее выражение в системе координат, совпадающей с ориентацией материала:

	■ 0	1/2	а"
D J =	1/2	0	0	.                     (2)
	_ 0	0	0 ]

Упругий потенциал предполагает зависимость от параметров трехосности и сдвига:

Ф = 1 J (Е , Q Н о к, .            (3)

В случае плоского напряженного состояния параметр Е ограничен - 3/2 < Е <  3/2, а определяющие соотношения на основе потенциала (3) принимают форму

^Е 11 = A 1111 ^(Е) ° 11 + A 1122 ^(Е) ° 22 +

+

13)3

— + -Е о--Еоп

3Е 2 J    2

^ф 1 О д ²,

Г      ,     ,       1 8A1212 (Е, Q))

е₁₂ = М121 г(Е, Q )о_п+--------- —Е^ф1 О₀² о,₂,

12          1212            11                                      1  012

^              2    dQJ

^Ф 1 = 2 [ A 1111 ^(Е)о 11 ⁺ A 2222 ^(Е)о 22 ⁺

+ 2A1122 (Е)опо22 + A1212 (Е)о22 ], где штрихом обозначена производная по параметру Е и, согласно уравнениям (1) и (2), зависимость от параметра Q остается только у коэффициента A212 (Е, Q).

Если задать коэффициент A ₂₁₂ (Е, Q ) в виде полинома    А ₁₂₁₂ ( Е , Q ) = ^ С ( E ) Q n   и сделать замену

n

B_n (Е) = ( 1 + п /2 ) С „ (Е) , то соотношение для деформации сдвига примет вид

^Е 12

B ( Е , Q ) ---Фо   о 12 ,

где функция B (Е , Q ) может быть приближена произвольным полиномом.

Определение функциональных зависимостей для коэффициентов A _Н(Е , Q ) является сложной задачей и требует трудоемких экспериментов на комбинированное нагружение. На практике можно использовать кусочно-линейные функции, и в целях уменьшения количества параметров модели принять

A 1111 ( ^Е ) = « 01 ^{+ С}11 ^Е ,

A 2222 ( Е ) = « 202 + c 22 Е ,                   (6)

A1122 (Е) = «12 + С12Е с постоянными а0 и су .

Коэффициенты A_ijk, (Е) в общем случае не произвольные. В частности, коэффициенты должны обеспечивать положительную определенность упругого потенциала (3). Положительная определенность потенциала может быть проверена численно для значений Е между -2/3 и +2/3 в случае плоского напряженного состояния.

Для случая чистого сдвига Е = 0 соотношение (5) принимает вид е₁₂ = B (0, Q )о₁₂. Если далее сделать предположение о независимости функции B (Е , Q ) от Е , т.е. B (Е , Q ) = B ( Q ) , и представить B ( Q ) как полином третьей степени по аналогии с работой [21], получится следующее соотношение для сдвиговой деформации:

+

--1--

3 Е 2

—

³     л _- 2

2 ^Ео 22 ^Ф 1 ^О 0 ,

^Б 12

2 у ^{+ ао} 12   3^ЕФ 1 ^о0

^о 12 ,

где G – постоянный модуль сдвига на начальной стадии деформирования, а коэффициент α подбирается исходя из нелинейной сдвиговой диаграммы.

С учетом сделанных предположений и выведенного на их основе выражения (7) остается сделать выбор параметров в (6).

2.    Эксперимент по нагружению тонкостенной цилиндрической оболочки с ребрами жесткости

Экспериментальная работа [30] по нагружению на сжатие цилиндрической оболочки с ребрами (рис. 1) до разрушения выбрана в качестве демонстрационной задачи. Испытываемая оболочка имеет внутренний диа- метр 700 мм и общую длину 700 мм, включая кольцевидные утолщения сверху и снизу для закрепления в испытательном оборудовании. Конструкция жестко зафиксирована через кольцевидные утолщения и нагружена сжатием до разрушения. Рабочая длина ограничена в пределах центральной части высоты цилиндра и равна 540 мм. Оболочка усилена восемью уголками L-сечения, равномерно распределенными в окружном направлении. Свободный край ребра жесткости имеет длину 25 мм, а фланец, прикрепленный к цилиндрической оболочке, имеет длину 32 мм. Размеры конструкции представлены в табл. 1. Оболочка из углепластика на основе тканевой ленты имеет свойства, указанные в табл. 2.

б

в

Рис. 1. Конструкция из композиционного материала для демонстрационной задачи [30]: а – вид внутри; б – зона ребра жесткости снаружи; в – общий вид установленной конструкции перед испытанием

Fig. 1. Composite structure for the demonstration problem: a – is an inside view; b – is an area of stiffener from outside; c – is an general view of setup before test

Таблица 1

Характеристики цилиндрической оболочки и ребер жесткости [30]

Table 1

Characteristics of the cylinder shell and stiffeners

Параметр	Значение
Диаметр цилиндра, мм	700
Длина цилиндра, мм	700
Ребра жесткости:
Количество	8
длина, мм	700
размеры L сечения, мм	25×32
Укладка:
Оболочка	[+45°/–45°]
Оболочка (усиления)	[+45°/–45°/0°/+45°/–45°]
Ребра	[0°/90°] 2S
Кольцо:
высота, мм	40
Укладка	[0°/90°] 2S

Таблица 2

Свойства материала монослоя [20]

Table 2

Layer properties

Параметр	Значение
Модуль Юнга, E11, МПа	57 765
Модуль Юнга, E22, МПа	53 686
Модуль сдвига, G12, МПа	3065
Коэффициент Пуассона, ν12	0,048
Плотность, ρ, кг/м3	1510
Толщина монослоя, мм	0,33

3.    Конечно-элементная модель

На основе экспериментальных данных, приведенных в предыдущем подразделе, была разработана конечно-элементная модель цилиндрической конструкции для моделирования процесса деформирования с использованием расчетного комплекса ABAQUS. Модель содержит около 18 000 оболочечных элементов S4R со средним размером 10 мм (рис. 2). Оба края оболочки с ребрами закреплены по всем степеням свободы для обеспечения фактической рабочей длины 540 мм между кольцами утолщения, за исключением степени свободы для нагружения края. Задача о нагружении конструкции рассматривается в динамической постановке, и для анализа был выбран решатель ABAQUS Implicit с неявной схемой интегрирования. Использование динамической постановки обусловлено проблемами сходимости при реализации численных методов статического анализа при закритическом поведении конструкции. При этом период времени нагружения конструкции подобран достаточно большим, так что его дальнейшее увеличение не оказывает влияния на результат ( T = 3 с). Кроме того, размер сетки был подобран с условием несущественного влияния на результат при ее дальнейшем измельчении для обеспечения сходимости. Используется нелинейная упругая модель материала, представленная в разд. 1, численно реализованная с помощью подпрограммы UMAT.

Рис. 2. Конечно-элементная модель цилиндрической оболочки с ребрами

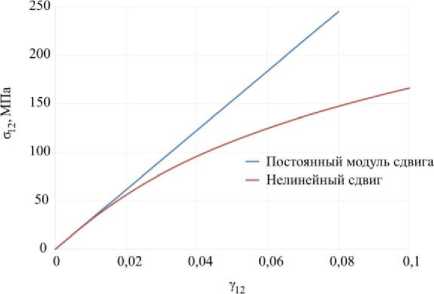
Рис. 4. Нелинейная диаграмма сдвигового нагружения (7) с α= 10 ^{- 8} (МПа^–3), γ ₁₂ = 2 ε ₁₂

Fig. 4. Nonlinear shear diagram with α= 10 ^{- 8} (MPa^–3), γ 12 = 2 ε 12

Fig. 2. Finite element model of the cylinder shell with stiffeners

4.    Анализ результатов

На рис. 3 показаны экспериментальная диаграмма нагружения сжатия цилиндра, диаграмма, полученная с использованием линейной упругой модели, и диаграмма, полученная с использованием определяющих соотношений, рассмотренных в разд. 2. Для определяющих соотношений использованы коэффициенты, представленные в табл. 3. Для сдвиговой деформации (7) подобран параметр α= 10 ^{- 8} (МПа^–3), реализующий диаграмму, показанную на рис. 4. Значения из табл. 3 определены неоднозначно из-за наличия экспериментальных данных только лишь на одноосное нагружение. Но эти значения хорошо согласуются с имеющимися одноосными испытаниями (см. табл. 2) и экспериментальной диаграммой сжатия всей конструкции (см. рис. 3). Отметим существенное расхождение с линейной моделью даже на начальном этапе нагружения.

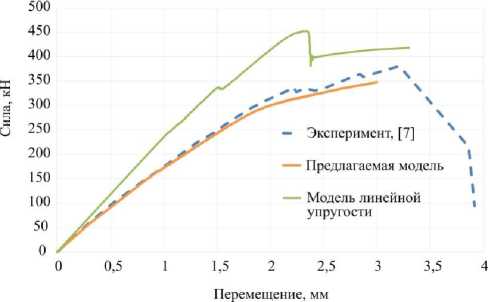
Рис. 3. Диаграммы нагружения

Fig. 3. Loading diagrams

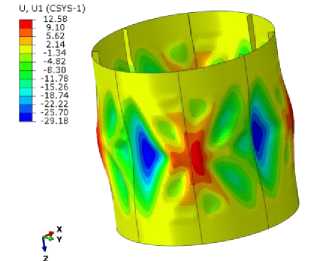
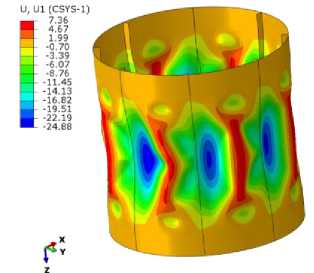
На рис. 5 показаны прогибы цилиндрической оболочки в нормальном направлении к поверхности (т.е. радиальные перемещения) перед полным разрушением, что соответствует перемещению захватов 3 мм. Предложенная в разд. 1 модель позволила получить формы прогибов, гораздо более близкие к экспериментальным, чем рассчитанные на основе линейной модели [30].

Таблица 3

Значения коэффициентов для определяющих соотношений (6) (МПа–1)

Table 3

The values of the coefficients for the defining relations (6) (MPa–1)

α 101	α 22	с 11	с 22	0 α 12	0 с 12
3,85E-03	3,85E-03	-4,4E-03	-4,4E-03	-2E-3	2E-3

б

Рис. 5. Перемещения оболочки (мм) в радиальном направлении перед разрушением (отображены в масштабе): а – модель линейной упругости; б – предложенная модель

Fig. 5. Displacements of the shell (mm) in a radial direction before failure (scaled to factor 2): ( a ) is a linear elasticity model, ( b ) is the proposed model

Согласно результатам испытания, в материале оболочки не было обнаружено повреждений вплоть до разрушения, вызванного потерей устойчивости ребер жесткости. На этом основании для рассматриваемой задачи нет необходимости вводить модель повреждения материала оболочки.

На рис. 6 представлено распределение параметра трехосности на внешней поверхности оболочки с использованием линейной и предложенной модели для уровня 20 и 100 % от разрушающей нагрузки. Для случая 20 % нагрузки еще не проявились эффекты, связанные с потерей устойчивости оболочки, и распределение параметра трехосности примерно одинаково.

Перед разрушением же картина абсолютно различная. Для линейно-упругой модели материала распределение параметра трехосности качественно различается на разных уровнях нагрузки (рис. 6, а , в ) в силу локальных прогибов оболочек, связанных с учетом геометрической нелинейности. Отметим также, что в случае предложенной модели основные области поверхности оболочки лежат вблизи предельных значений, соответствующих двухосному сжатию ^ = - 2 / 3 и двухосному растяжению ^ = + 2 / 3 . Это означает, что использование экспериментальных данных на двухосное нагружение необходимо для точного моделирования.

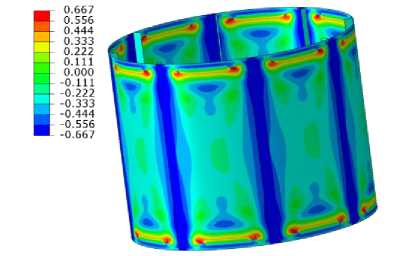
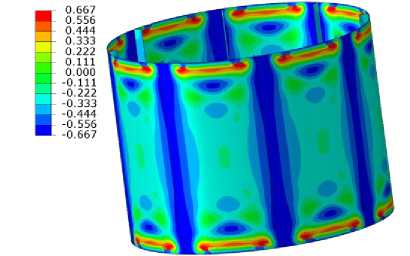
а                                                 б

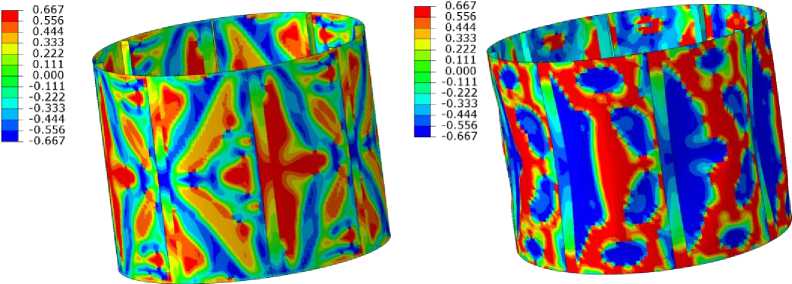
г

Рис. 6. Распределение параметра трехосности ^ : а - модель линейной упругости, 20 % от разрушающей нагрузки;

б – предложенная модель, 20 % от разрушающей нагрузки; в – модель линейной упругости перед разрушением;

г – предложенная модель перед разрушением

Fig. 6. Triaxiality parameter distribution before failure ^ : (a) is the linear elastic model, 20% of failure load, (b) is the proposed model, 20% of failure load, (c) is the linear elastic model, before failure, (d) is the proposed model, before failure

Заключение

Численная реализация модели анизотропного упругого материала, восприимчивого к виду напряженного состояния и нелинейному сдвигу, показала хорошую корреляцию моделирования с экспериментом для демонстрационной задачи о потере устойчивости тонкостенной конструкции. Дальнейшая разработка модели для случая трехмерного напряженного состояния в сочетании с моделью повреждаемости выглядит перспективным и эффективным инструментом для инженерных приложений.

Работа выполнена при финансовой поддержке РФФИ (грант № 18-31-20026).

Acknowledgment

The work has been made with the financial support of The Russian Foundation for Basic Research (Grant No. 18-31-20026).

Библиографический cписок

• 1.    COCOMAT–improved material exploitation of composite airframe structures by accurate simulation of postbuckling and collapse / R. Degenhardt [et al.] // Composite Structures. – 2006. – Vol. 73. – No. 2. – P. 175–178.

• 2.    Babaei H., Kiani Y., Eslami M.R. Geometrically nonlinear analysis of shear deformable FGM shallow pinned arches on nonlinear elastic foundation under mechanical and thermal loads // Acta Mechanica. – 2018. – Vol. 229. – P. 3123–3141.

• 3.    Effect of material nonlinearity on buckling and postbuckling of fiber composite laminated plates and cylindrical shells / S.S. Wang [et al.] // Composite Structures. – 1995. – Vol. 33. – No. 1. – С. 7–15.

• 4.    Zhang L., Gao Q., Zhang H.W. An efficient algorithm for mechanical analysis of bimodular truss and tensegrity structures // International Journal of Mechanical Sciences. – 2013. – Vol. 70. – С. 57–68.

• 5.    Bruno D., Lato S., Zinno R. Nonlinear analysis of doubly curved composite shells of bimodular material // Composites Engineering. – 1993. – Vol. 3. – No. 5. – P. 419–435.

• 6.    Li Z.M., Liu T., Yang D.Q. Postbuckling behavior of shear deformable anisotropic laminated cylindrical shell under combined external pressure and axial compression // Composite Structures. – 2018. – Vol. 198. – С. 84–108.

• 7.    Patel B.P., Khan K., Nath Y. A new constitutive model for bimodular laminated structures: Application to free vibrations of conical/cylindrical panels //Composite Structures. – 2014. – Vol. 110. – P. 183–191.

• 8.    Khan K., Patel B.P., Nath Y. Dynamic characteristics of bimodular laminated panels using an efficient layerwise theory // Composite Structures. – 2015. – Vol. 132. – P. 759–771.

• 9.    Khan K., Patel B.P., Nath Y. Free and forced vibration characteristics of bimodular composite laminated circular cylindrical shells // Composite Structures. – 2015. – Vol. 126. – P. 386–397.

• 10.    Yao W., Zhang C., Jiang X. Nonlinear mechanical behavior of combined members with different moduli // International Journal of Nonlinear Sciences and Numerical Simulation. – 2006. – Vol. 7. – No. 2. – P. 233–238.

• 11.    Fraternali F., Spadea S., Ascione L. Buckling behavior of curved composite beams with different elastic response in tension and compression // Composite Structures. – 2013. – Vol. 100. – P. 280–289.

• 12.    Jones R.M. Stress-strain relations for materials with different moduli in tension and compression // AIAA Journal. – 1977. – Vol. 15. – No. 1. – P. 16–23.

• 13.    Lomakin E.V., Rabotnov Yu. N. A theory of elasticity for an isotropic body with different moduli in tension and compression // Mechanics of Solids. – 1978. – Vol. 13. – No. 6. – P. 25–30.

• 14.    Medri G. A nonlinear elastic model for isotropic materials with different behavior in tension and compression // Journal of Engineering Materials and Technology. – 1982. – Vol. 104. – No. 1. – С. 26–28.

• 15.    Ambartsumyan S.A., Khachatryan A.A. Theory of weak-moment shells made from varying-modulus material // International Applied Mechanics. – 1969. – Vol. 5. – No. 5. – С. 447–454.

• 16.    A new computational framework for materials with different mechanical responses in tension and compression and its applications / Z. Du [et al.] // International Journal of Solids and Structures. – 2016. – Vol. 100. – P. 54–73.

• 17.    Vijayakumar K., Ashoka J.G. A bilinear constitutive model for isotropic bimodulus materials // Journal of Engineering Materials and Technology. – 1990. – Vol. 112. – No. 3. – P. 372–379.

• 18.    A review on the research of mechanical problems with different moduli in tension and compression / J. Sun [et al.] // Journal of Mechanical Science and Technology. – 2010. – Vol. 24. – No. 9. – P. 1845–1854.

• 19.    Convergence analysis of a finite element method based on different moduli in tension and compression / X. He [et al.] // International Journal of Solids and Structures. – 2009. – Vol. 46. – No. 20. – P. 3734–3740.

• 20.    An efficient finite element formulation for nonlinear analysis of clustered tensegrity / L. Zhang [et al.] // Engineering Computations. – 2016. – Vol. 33. – No. 1. – P. 252–273.

• 21.    Hahn H.T., Tsai S.W. Nonlinear elastic behavior of unidirectional composite laminae // Journal of Composite Materials. – 1973. – Vol. 7. – No. 1. – P. 102–118.

• 22.    Sabik A. Direct shear stress vs strain relation for fiber reinforced composites //Composites Part B: Engineering. – 2018. – Vol. 139. – P. 24–30.

• 23.    Van Paepegem W., De Baere I., Degrieck J. Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part II: Model development and finite element simulations // Composites Science and Technology. – 2006. – Vol. 66. – No. 10. – P. 1465–1478.

• 24.    Mechanisms of shear deformation in fiber-reinforced polymers: experiments and simulations / E. Totry [et al.] // International journal of fracture. – 2009. – Vol. 158. – No. 2. – P. 197–209.

• 25.    Lomakin E.V., Fedulov B.N. Nonlinear anisotropic elasticity for laminate composites // Meccanica. – 2015. – Vol. 50. – No. 6. – С. 1527–1535.

• 26.    Lomakin E.V., Fedulov B.N., Melnikov A.M. Constitutive models for anisotropic materials susceptible to loading conditions // Mechanics and Model-Based Control of Advanced Engineering Systems. – Vienna: Springer, 2014. – P. 209–216.

• 27.    Lomakin E.V. Constitutive models of mechanical behavior of media with stress state dependent material properties // Mechanics of Generalized Continua. – Berlin: Heidelberg, Springer, 2011. – P. 339–350.

• 28.    Failure analysis of laminated composites based on degradation parameters / B.N. Fedulov [et al.] // Mechanica. – 2018. – Vol. 53. – No. 1–2. – P. 359–372.

• 29.    Nonlinear shear behavior and failure of composite materials under plane stress conditions / B. Fedulov [et al.] // Acta Mechanica. – 2017. – Vol. 228. – No. 6. – P. 2033–2040.

• 30.    Bisagni C., Cordisco P. Post-buckling and collapse experiments of stiffened composite cylindrical shells subjected to axial loading and torque // Composite Structures. – 2006. – Vol. 73. – No. 2. – P. 138–149.