Задача стартового управления и финального наблюдения для системы уравнений Фитцхью-Нагумо с условием Дирихле-Шоуолтера-Сидорова

Пусть Qc Rⁿ - ограниченная область с границей 3Q класса C ” . В цилиндре Q = Qx (0, T ) рассмотрим вырожденную систему уравнении Фитц Хью - Нагумо:

'0 = «jAv + Д w - П1 v + fi,(1)

‘ d w      „ оз

— = « 2 ^A w ⁺ p _Tw ^- % v ^{- w + f} 2

l О t с краевым условием Дирихле

v(s,t) = 0,w(s,t) = 0,(s,t)e dQ x(0,T)

и начальным условием Шоуолтера-Сидорова w (s ,0) = u (s), s eQ.(3)

Искомые функции w=w(s,t) и v = v(s,t) описывают динамику мембранного потенциала и поведение натриевого и калиевого токов; в2 e R- , «,в1,«1,«2,П1,П2 e R + - характеризуют порог возбуждения, скорость порога возбуждения, электропроводность и реполяризацию среды; f = ( f1, f 2) - источник возбуждения. Первоначально в работах [1, 2] была получена невырожденная система уравнений Фитц Хью-Нагумо, зависящая от двух искомых функций v и w, мо- делирующих поведение химических элементов в мембране. Скорость искомой функции w увеличивается по мере ее роста, что привносит в систему сильную нелинейность. Невырожденная система уравнений Фитц–Хью в двухкомпонентном и многокомпонентном случаях изучалась подробно в работах [3-5]. Нулевое решение невырожденной системы при в2 < 0 асимптотически устойчиво, а при в2 > 0 неустойчиво [6]. В связи с тем, что скорость искомой функции w существенно превосходит скорость изменения v, в случае устойчивости решения (при в2 < 0) в работе [7] было предложено рассматривать именно вырожденную систему уравнений вида (1). Нами будет рассмотрен случай асимптотически устойчивой задачи, когда в2 < 0 и Р1 = п2 .

Начально-краевая задача (2), (3) для системы уравнений (1) в специальным образом подобранных функциональных пространствах редуцируются к задаче Шоуолтера–Сидорова для абстрактного полулинейного уравнения

Lx + Mx + N ( x ) = f , ker L Ф {0}                             (5)

и относится к широкому классу уравнений соболевского типа [8, 9]. При рассмотрении классического условия Коши в случае уравнений соболевского типа решение задачи существует лишь при начальном значении u ( s ) взятом из фазового пространства уравнения (5). Рассматриваемое в работе условие Шоуолтера–Сидорова (4) является более общим по сравнению с условием Коши и позволяет снять данное ограничение. Впервые задача управления для уравнений соболевского типа была поставлена и изучена в конце XX века, задачи же стартового управления и финального наблюдения исследуются сравнительно недавно. Задачи управления для полулинейных уравнений соболевского типа с условием Шоуолтера–Сидорова рассматривались в [10, 11]. В работе [12] была исследована задача оптимального управления для вырожденной системы уравнений (1), а также рассмотрены и доказаны существование и единственность решения задачи (1)–(3) в слабом обобщенном смысле. Впервые задача стартового управления и финального наблюдения для системы уравнений (1) рассматривалась в работе [13].

Данная работа посвящена исследованию задачи стартового управления и финального наблюдения

J ( x ( T ) ,u ) ^ inf                                     (6)

решениями задачи (1)–(3) в слабом обобщенном смысле [8, 14]. Задача стартового управления и финального наблюдения моделирует ситуацию, когда после кратковременного управляющего воздействие ожидается требуемый результат за некоторый период времени, т. е. в начальный момент времени посылается импульс большой мощности в систему нервов и ожидается требуемое состояние системы через некоторое установленное время. В работах [15–17] изучались задачи стартового управления и финального наблюдения для различных математических моделей, основанных на уравнениях соболевского типа.

• 1.    Задача стартового управления и финального наблюдения o

Положим H i = W ₂ 1 ( Q ) и B i = L ₄ ( Q ) , i = 1,2. Рассмотрим гильбертово пространство A = L ₂ ( Q ) x L ₂ ( Q ) со скалярным произведением

^{[ x Z ]} = vV , ^ l 2 ( q ) ⁺ ( ^w , ^ L 2 ( Q ) , где ^x = ⁽ v , w ), ^Z = ^ ).

Определим пространства H = H 1 x H ₂ и B = B 1 x B ₂ , а через H * , B * обозначим сопряженные пространства к пространству H , B относительно скалярного произведения в A , соответственно. В силу теоремы Соболева в случае n <  4 имеют место плотные и непрерывные вложения

H с B с A с B * с H *, причем вложение H с A компактно согласно теореме Реллиха-Кондрашева.

Определим операторы L,M,N следующим образом:

[ Lx,Z ] = к w,n ) ,x,Z g H ,

Замечание 1. Операторы L,M e L ( H;H * ) линейные непрерывные операторы. Справедливость данного утверждения является классическим результатом.

Рассмотрим пространство

X = { x | v e L 2 ( 0, T ; H 1 ) , w e L _ ( 0, T ;coim L ) n L ₄ ( 0, T ; B 2 ) }.

Определение 1. Вектор-функцию x e X при T e R₊ назовем слабым обобщенным решением задачи Шоуолтера-Сидорова (1)-(3), если она удовлетворяет

T

И t ) I LdX ^, 0 VL d

^Z + l Mx +

T

Теорема 1. [13] Пусть a ₁, a ₂, Р ₁, П ₁ e R ₊ , P ₂ e R - и n - 4 , тогда при любых x ₀ e H , T e R ₊ f _ e L ₂ ( 0, T ; H _w * ) , f , e L ₄ ( 0, T ; B 2 ) , u e H ₂ существует единственное решение x e X задачи (1)-

(3), причем

IIw (t )l IL 2W

t

t

t

⁺ C W f Ll ^{V T} )| Hh , ⁺l l ^{w (Т} )| B ₂ ] ^{d T -} C 2 fl k w ^Т )| H * ^{d T +} C 3 ill ^f 2 ^{Т )}| I B ₂ ^{d T +} l l u l ^( П ) ,

' 2

C i > 0 ,i = 1 , 3 .                                                  (7)

Пусть J ( x ( T ) ,u ) - ограниченный снизу, полунепрерывный снизу, коэрцитивный функционал; u e U ad , где U ad - некоторое замкнутое и выпуклое множество в пространстве управлений U = H ₂ . Рассмотрим задачу стартового управления и финального наблюдения (6) решениями (1) - (3) в слабом обобщенном смысле.

Определение 2. Пару ( x ( T ) ^U ) e X х U ad будем называть решением задачи (1)-(3), (6), если J (, x ( T ), Ui) = inf J ( x ( T ), u ),

( x , U )

и пары ( x,u ) удовлетворяют задаче (1)-(3) в смысле определения 1. Вектор-функцию и будем называть стартовым управлением задачи (1)-(3), (6).

Теорема 2. Пусть a ₁, a ₂, Р ₁, П ₁ e R ₊ , Р ₂ e R - , T e R ₊ и n - 4 , тогда существует решение ( 5с ( T ) ,й ) задачи (1)-(3), (6).

Доказательство. В силу теоремы 1 для задачи (1)-(3), (6) для любого u e U ad существует единственное слабое обобщенное решение. Следовательно, можно считать, что

J (x (T) ,u) = J (u).

• I.    Множество значений функционала ограничено снизу, значит, существует минимизирующая последовательность {u m } с U ad , такая что

• lim J (um ) = C,

m ^^

где C - точная нижняя грань множества значений функционала J ( x ( T ) ,u ) . Последовательность { J ( u_m ) } [ m = ₁ ограничена в R, следовательно, в силу коэрцитивности функционала J ( u ) , последовательность { u_m } [ m = ₁ ограничена в U. Согласно теореме Банаха-Алаоглу из { u_m } можно извлечь слабо сходящуюся подпоследовательность u_m ^ й в U. В силу теоремы Мазура точка ui e U ad .

• II.    Обозначим за x_m=x ( u_m ) = ( v_m,w_m ) = ( v ( u_m ) ,w ( u_m ) ) последовательность слабо обобщенных решений задачи

Lx^ m ^{+ Mx}m ⁺ N ( ^xm ) = f , ^L ( ^xm ( ⁰ ) ^{- u}m ) = ⁰ .

Гаврилова О.В.

В силу теоремы 1 и оценки (7) и, ввиду рефлексивности бохнеровских пространств L4 (0,T; B*), L* (0, T; H1) и L4 (0, T; B*) существуют слабые пределы vm ^ V слабо L* (0, T; H1), Wm ^ W *-слабо L_(0, T; L*(Q)), wm ^ W слабо L4 (0, T; B*).

В силу ограниченности операторов L и M получим

^[ Um ⁽ t ) , x m ⁽ t ) ] < | Lx m ⁽ t )| H* ||^xm ⁽ t )| H <  C L || x _m ⁽ t )| H ,

[Mm (t ), xm ( t)] < |Mxm ( t)|H* ||xm (t )|H < CM ||xm ( t)|H , значит {Lxm},{Mxm} ограничены в L„ (0,T;H ).

По построению оператора N получим, что

TT

J[N(xm ),xm ] dT = j||wm|B*|wm ||B* dT и {N(xm)} ограничена в L4 (0,T;B*) следовательно,

N ( x m ) ^ M слабо в L 4 ( 0, T ; B *) .

• III.    Покажем, что ц = N ( X ) , где X = ( V,w ) . Так как пространство H c A компактно, то последовательность w m ^ w в пространстве L * ( 0, T ; L * ( Q ) ) . Получим, что

• в силу единственности предела.

• IV.    Так как пространство A сепарабельно, то выберем в нем счетную всюду плотную орто-нормированную систему функций { ф } } = { ( ф 1 , ф * ) } . Тогда в силу основной леммы вариационно-

• го исчисления

T

Зафиксируем j и перейдем к пределу при m ^ +^

T

Тогда получим, что

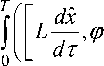
Следовательно, 5c = x (й) и в силу полунепрерывности снизу функционала J, получим lim inf J(um) > J(й). Значит u есть стартовое управление в задаче (1)-(3), (6). Таким образом, m ^” Uad теорема доказана.

Рассмотрим задачу стартового управления и финального наблюдения (1)–(3), (6), где функционал штрафа задается формулой

^{J ( X ( T} ) , u ) = ^|| v ^{( T ) -} vf ||H 1 ⁺ ^| w ^{( T ) -} w f I B * ⁺ M u i H * .                      ⁽⁸⁾

Здесь X f ( s ) = ( V f ( s ) ,W f ( s ) ) - требуемое состояние системы, которого достигается при минимальном начальном воздействии по прошествии времени t = T .

Лемма 1. Функционал J ( x ( T ) ,u ) , заданный в виде (8), является ограниченным снизу, полунепрерывным снизу, коэрцитивным функционалом.

Доказательство. Покажем, что функционал J ( x ( T ) ,u ) , заданный в виде (8), является коэрцитивным

• ⁵ C l ( T ) - ” / 1 , 1 + C 2I I » ( T ) - » / 1 С 2 + C з +1 м H 2 =- , и С 2 + C i ^ ,¹- иt 2 =

• = C , ( , V ( T ) - V y|, + , » ( T ) - » y|, 2 + ( 1 - в )| и , 2 ) + C 6 = C , ( J ( x , u ) ) + C 6 , C, > 0, i = 1,6, C 3 >  3 при C 2 = 4| »_z|_s 2 .

Очевидно, что функционал J ( x ( T ) ,u ) непрерывный, а значит, и полунепрерывный снизу. Таким образом, лемма доказана.

В силу теоремы 2 и леммы 1 справедлива

Теорема 3. Пусть а , , а ₂, в ₁, П ₁ ^е R ₊ , Р ₂ ^е R - , T ^е R ₊ и n 5 4 , тогда существует решение (. x ( T ) /ui ) задачи (1)-(3), (6), где функционал J ( x ( T ) ,u ) принимает вид (8).

Автор выражает признательность профессору Н.А. Манаковой за постановку задачи и плодотворные дискуссии, а также профессору А.В. Богомолову за интерес к работе. Кроме того, считает своим приятным долгом поздравить профессора А.В. Богомолова с юбилеем.