Задачи оперативного управления проектами

Задачи оперативного управления проектами возникают на стадии анализа и регулирования проекта. Необходимость корректировки предметной области (целей и состава работ) или календарного плана появляется либо по требованию заинтересованных лиц, либо с целью снижения потерь (штрафов) при отклонении состояния проекта от плана. Суть задачи оперативного управления заключается в снижении продолжительности работ проекта за счет проведения ряда мероприятий. В непрерывном случае, когда затраты на снижение продолжительности работ являются выпуклыми функциями величины снижения, задачи рассматривались в работах [1, 2] для линейных зависимостей, в [3] для выпуклых зависимостей и существуют эффективные алгоритмы их решения. В дискретном случае, когда затраты на снижение продолжительностей работ являются дискретными функциями величины снижения, задача является сложной (NP-трудной) задачей дискретной оптимизации. В работе предложен эффективный алгоритм решения задачи для случая, когда функции затрат являются дискретными, а сетевые графики являются деревьями или агрегируемыми сетями [4]. Для общего случая предложен метод ветвей и границ.

Постановка задач (дискретная модель)

Рассмотрим сетевой график, содержащий n работ (работы изображаются вершинами). Обозначим т i - продолжительность работы i 6 X ( X - множество всех работ). Для каждой работы i задана величина Δ i возможного сокращения ее продолжительности и затраты s i на это сокращение. Обозначим T – длину критического пути при продолжительностях работ τ _i j , T ₀ – требуемая продолжительность проекта ( Q = T – T 0 – требуемое сокращение). Обозначим x i = 1, если продолжительность работы i сокращается на Δ i , x i = 0 в противном случае.

Задача 1 . Определить { x i } , i 6 X, так чтобы продолжительность проекта была не больше T 0 , а суммарные затраты на снижение продолжительностей работ

S ( x ) = S t 6 х s t X i                                                                                     (1)

были минимальными.

Частный случай сетевого графика (дерево)

Пусть сетевой график является деревом (рис. 1)

Краткие сообщения

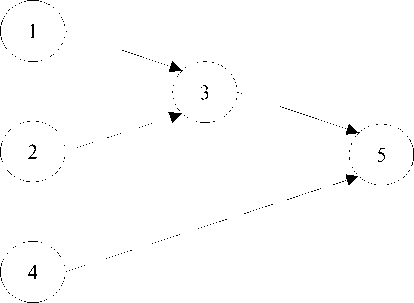
Рис. 1. Сетевой график в виде дерева

Примем, что вершины, соответствующие работам, имеют правильную нумерацию (дуги идут от меньших номеров к большим).

Рассмотрим две ситуации.

Ситуация 1 (веер) . Имеются k независимых работ, у которых общая непосредственно следующая вершина (рис. 2).

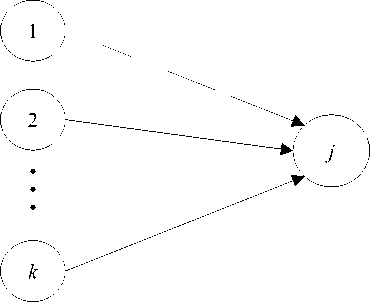
Рис. 2. Сетевой график с общей непосредственно следующей вершиной

Задача заключается в определении минимальных затрат, при которых продолжительность подпроекта (рис. 2) не превышает некоторой величины ξ.

Алгоритм решения задачи

• 1.    Определяем множество R работ, таких, что T i < ^. Полагаем x i = 0 для i 6 R.

• 2.    Для остальных работ (τ i > ξ) полагаем x i = 1.

Решение задачи, очевидно, существует для ^, удовлетворяющего условию ^ > max ; (т i - A i ).

Пример 1 . Рассмотрим сетевой график на рис. 1. Данные о работах приведены в табл. 1.

Таблица 1

i	1	2	3	4	5
τ i	10	9	8	14	6
Δ i	4	5	5	8	3
S i	6	8	4	9	7

Рассмотрим работы 1 и 2. Это независимые работы с общим конечным событием (ситуация 1).

Имеем ξ ≥ 5. Меняем ξ от 6 до 10. Получаем зависимость минимальных затрат S от суммарной продолжительности ξ (табл. 2) .

Таблица 2

ξ	10	9	5
S	0	6	14

Ситуация 2 . Имеются две последовательные работы i и j , для которых заданы зависимости S i ^(E i ) и ^Sj (E j ) ( d i < E i , d j <  ^ j ).

Требуется определить зависимость минимальной суммы затрат s (ξ), при которых сумма продолжительностей этих работ не превышает ξ . Решение существует для ξ, удовлетворяющих условию d i + d j ≤ ξ .

Алгоритм решения

Построим таблицу, нижняя строка которой соответствует парам ( S i ; E ii ) в очередности возрастания E ii , а левый столбец соответствует парам ( S j ; E jj ) в очередности возрастания E jj . В клетках ( i , j ) таблицы помещаем пару ( S i + S j ; E i +E j ). Строим зависимость S (E), выбирая из всех клеток с одинаковыми E клетку с минимальной суммой s = S i + S j .

Пример 2 . В примере 1 была получена зависимость S j (E I ) обобщенной работы I = (1, 2) от суммарной продолжительности ξ I (табл. 1). Рассматриваем работу 3 и обобщенную работу (1, 2). Строим табл. 3.

Таблица 3

4; 3	4; 13	10; 12	18; 11	22; 9
0; 8	0; 18	6; 17	14; 16	18; 14
3 I	0; 10	6; 9	14; 8	18; 6

Итоговая табл. 4 имеет вид

Таблица 4

S 123	0	4	10	18	22
ξ 123	18	3	12	11	9

Из таблицы удалены заведомо не оптимальные варианты. Так, вариант (6; 17), безусловно, проигрывает варианту (4; 13), поскольку при меньших затратах получаем меньшую суммарную продолжительность. Аналогично, варианту (4; 13) проигрывают варианты (14; 16) и (18; 14).

Таким образом, алгоритм решения задачи состоит в последовательном рассмотрении либо ситуации 1, либо ситуации 2. Так, после получения табл. 2 для обобщенной работы II = (1, 2, 3) мы снова получаем ситуацию 1 с обобщенной работой (II) и работой 4.

Применяя алгоритм для ситуации 1, получаем таблицу зависимости минимальных затрат от продолжительности выполнения подсети III, состоящей из работ (1, 2, 3 и 4) (табл. 5).

Таблица 5

S III	0	4	13	19	27	31
ξ III	18	14	13	12	11	9

Обобщенная работа (III) и работа 5 образуют последовательную цепочку (ситуация 2). Решение приведено ниже (табл. 6).

Таблица 6

7; 3	7; 21*	11; 17	20; 16	26; 15	34; 14	38; 12
0; 6	0; 24	4; 20	13; 19*	19; 18*	27; 17*	31; 15*
5 III	0; 18	4; 14	13; 13	19; 12	27; 11	31; 9

Окончательная табл. 7 зависимости минимальных затрат от сокращения продолжительности проекта до величины T ₀ приведена ниже.

Таблица 7

S	0	4	11	20	26	34	38
T o	24	20	17	16	15	14	12

Краткие сообщения

Частный случай (агрегируемый сетевой график)

Рассмотрим другой частный случай, когда сетевой график является агрегируемым. В данном случае более удобным является представление сетевого графика в виде «работы – дуги». Множество дуг сетевого графика, у которых общие начальные и конечные события, называется параллельным множеством. Это соответствует ситуации 1. Поэтому множество таких дуг можно заменить одной дугой, решая задачу ситуации 1. Множество дуг, образующее путь в сетевом графике, при условии, что степени захода и исхода всех вершин пути (за исключением начальной и конечной) равны 1, называется последовательным множеством дуг. Это соответствует ситуации 2. Поэтому множество таких дуг можно заменить одной дугой, решая задачу ситуации 2. Если сетевой график является агрегируемым, то, решая задачи для ситуации 1 и (или) 2, мы сводим его к одной дуге. А это значит, что задача оперативного управления решена.

Определение. Сетевой график, который путем замены параллельных и (или) последовательных множеств дуг одной дугой, можно свести к одной дуге, называется агрегируемым.

Теорема 1 . Для того чтобы сетевой график был агрегируемым, необходимо и достаточно отсутствие в нем структур типа «мост» (рис. 3), при этом каждая дуга может быть последовательным множеством.

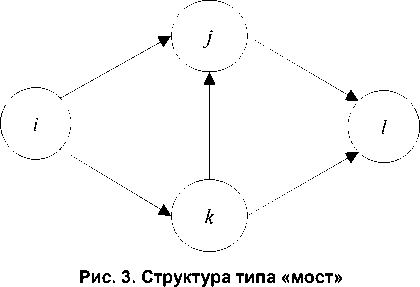
Доказательство . Необходимость очевидна, поскольку «мост» является неагрегируемым сетевым графиком.

Докажем достаточность. Пусть задан произвольный сетевой график без «мостов». Заменяя последовательные и (или) параллельные множества дуг одной дугой, сводим его к сетевому графику без параллельных дуг, степени исхода вершин которого больше 1. Пусть в полученном сетевом графике найдена вершина, отличная от конечной, степень захода которой больше 1 (рис. 4, вершина 5). Но в этом случае, как легко видеть, в сетевом графике появляется «мост», что противоречит предположению. Таким образом, все вершины сети, кроме конечной, имеют степени захода, равные 1. А такой сетевой график всегда является агрегируемым. Теорема доказана.

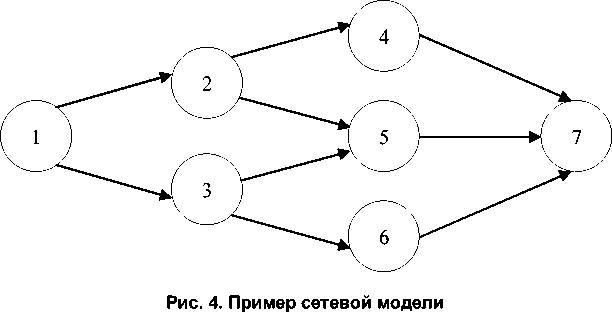
Пример 3 . Рассмотрим сетевой график на рис. 5.

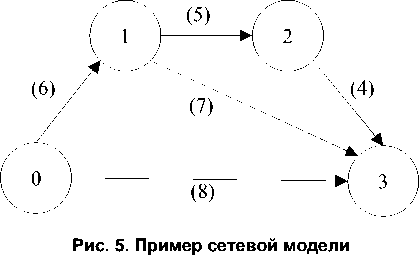
Данные о работах приведены в табл. 8.

Таблица 8

( i , j )	(0, 1)	(0, 3)	(1, 2)	(1, 3)	(2, 3)
τ ij	6	8	5	7	4
A- Δ ij	3	4	2	5	1
c ij	9	8	6	10	3

Примем T 0 = 12.

1 шаг . Рассматриваем последовательное множество дуг (путь (1, 2, 3)). Решение приведено в табл. 9. Результаты сведены в табл. 10.

Таблица 9

1	8; 3	6; 9
0	9; 0	7; 6
(2, 3) (1, 2)	0	1

Таблица 10

Вариант	0	1	2
Т	9	8	6
S	0	3	9

2 шаг . Рассматриваем параллельное множество дуг (1, 3) и (1, 3). Решение приведено в табл. 11.

Таблица 11

Вариант	0	1	2	3
Т	9	8	7	6
S	0	3	9	19

3 шаг . Рассматриваем последовательное множество дуг (0, 1) и (1, 3). Решение приведено в табл. 12.

Таблица 12

3; 9	12; 9	11; 12	10; 18	9; 28
6;0	–	–	–	12; 19
(0,1) (1,3)	9; 0	8; 3	7; 9	6; 19

Поскольку T 0 = 12, то работу (0, 3) не сокращаем. Оптимальное решение находим методом обратного хода. Оптимальное решение определяется клеткой (12; 9). Ей соответствует сокращение работы (0, 1) на 3 единицы.

Краткие сообщения

Общий случай

Любой сетевой график можно превратить в агрегируемый путем разделения ряда вершин на несколько вершин. На рис. 6 приведен пример преобразования «моста» в агрегируемый сетевой график.

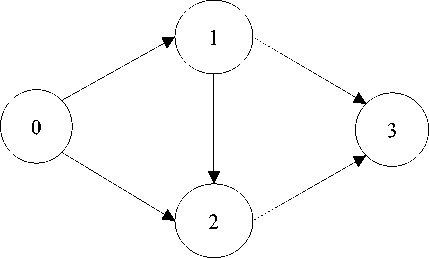
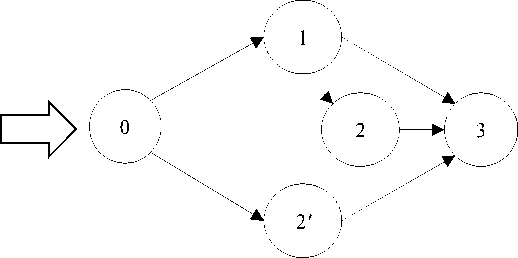
Рис. 6. Пример преобразования «моста» в агрегируемый сетевой график

При этом затраты S ij также делим на соответствующее число частей произвольным образом (в примере на рис. 6 на две части).

Теорема 2 . Решение задачи для преобразованного (агрегируемого) сетевого графика дает оценку снизу для исходной задачи.

Доказательство следует из очевидного факта, что любое допустимое решение исходной задачи является допустимым и для преобразованной задачи.

Следствие . Если в результате решения оценочной задачи получено допустимое решение, то оно является оптимальным.

Доказательство очевидно, поскольку в этом случае получена достижимая нижняя оценка.

Как отмечалось выше, деление затрат разделяемых работ является произвольным. Выбор значений этих переменных, максимизирующих нижнюю оценку, называется обобщенной двойственной задачей (ОДЗ).

Теорема 3 . Обобщенная двойственная задача является задачей выпуклого программирования.

Доказательство. Пусть Q - множество разделенных работ, и = {u^k j } - деление затрат работы ( i , j ) 6 Q , где k = 1, q 1 j - число работ, на которые делится работа ( i , j ). Пусть далее и ¹ и и ² - два допустимых решения ОДЗ, то есть

^_ки ^ = s_tj , ( i , j ) 6 Q .                                                                                (2)

Возьмем выпуклую линейную комбинацию u = α u1 + (1 – α) u2, 0 < α < 1.                                                                   (3)

Обозначим Ф( u ) значение целевой функции ОДЗ в зависимости от u , ( i , j ) ^k – k -го из разделенных работ работы ( i , j ) 6 Q, X^k j = 1, если продолжительность k -й работы сокращена, Х ц = 0, в противном случае, имеем

Ф (а и ¹ + (1 - а) и ²) = min x £_а ,_л 6 q S k [ а и^к ^ х^к/ + (1 - а)и^к х^к/] +

⁺ ^Ц.) 6 Q^Sij ^Xij >  ^а min x ^{[ S}(i,j) 6 Q ^Sk ^ j ^Xij ^{+ S}(i,j) 6 Q S ij ^Xij ^]+

^{+(1 - а)} min x ^{[ S}(i,j) 6 Q ^Sk ^{u k} f ^Xij ^{+ S}(i,j) 6 Q S ij ^Xij ^] = ^{а Ф и} 1 + ^{(1 - а) Ф ( и 2)} .

Пример 4 . Возьмем сетевой график на рис. 6. Данные о работах приведены в табл. 13. Возьмем U 23 = U 2₃ = 3 , Т 0 = 11.

Таблица 13

( i , j )	(0, 1)	(0, 2)	(1, 2)	(1, 3)	(2, 3)
τ ij	5	7	4	8	6
A- ij	2	3	1	4	3
s ij	10	12	18	9	6

1 шаг . Рассматриваем последовательное множество работ (2, 3), (1, 2). Решение приведено в табл. 14.

Таблица 14

3; 3	7; 3	10; 21
4; 0	8; 0	7; 18
(2, 3) (1, 2)	4; 0	3; 18

Результаты сведены в табл. 15.

Таблица 15

Вариант	0	1	2
Т	8	7	6
S	0	3	21

2 шаг . Рассматриваем параллельное множество работ (1, 3) и (1, 3). Решение приведено в табл. 16.

Таблица 16

Вариант	0	1	2
Т	8	7	6
S	0	12	30

3 шаг . Рассматриваем последовательное множество работ (0, 1) и обобщенную работу (1, 3).

Решение приведено в табл. 17.

Таблица 17

3; 10	11; 10	10; 22	9; 40
5; 0	–	–	11; 30
(0, 1) (1, 3)	8; 0	7; 12	6; 30

Оптимальное решение определяется клеткой (11, 10). Ему соответствует сокращение работы (0, 1) на 2 единицы.

4 шаг . Рассматриваем последовательное множество работ (0, 2 ' ) и (2 ' , 3). Решение приведено в табл. 18.

Таблица 18

4; 12	10; 12	7; 15
7; 0	–	10; 3
(0; 2 ' ) (2 ' , 3)	6; 0	3; 3

Оптимальное решение определяется клеткой (10; 3). Ему соответствует сокращение работы (2 ' , 3) на 3 единицы.

Полученное решение является недопустимым. Поэтому затраты 10 + 3 = 13 дают нижнюю оценку. Увеличим u |₃ до 6. Клетка (10, 6) по-прежнему определяет оптимальное решение. Оно является допустимым и поэтому оптимальным.

Окончательно сокращаем продолжительности работ (0, 1) (на две единицы) и (1, 3) (на 3 единицы) с затратами 16.

Заключение

Предложенные алгоритмы получения точного решения задачи оперативного управления либо нижних оценок являются эффективными, поскольку их вычислительная сложность определяется решением конечного числа задач с двумя дискретными переменными. Если не удалось получить точного решения, то нижние оценки можно использовать в методе ветвей и границ.

Краткие сообщения

Алгоритм естественным образом обобщается на случай, когда для каждой работы имеется несколько вариантов сокращения ее продолжительности.