Задачи пассивного поворота гусеничной машины (постановка, модель движения)

Теория поворота гусеничных машин развивалась сначала как теория управляемого криволинейного движения. Потребности практического проектирования скоростных машин и его научного обеспечения определили круг задач и методы их решения: расчёт тягового и мощностного балансов, условий заноса, устойчивости, управляемости и др. [3, 7, 14].

Развитие тракторного парка машин и современное производство тихоходных тяговых машин и агрегатов на их базе выдвигает необходимость постановки и решения проблем неуправляемого (пассивного) поворота со своими задачами и методами решений.

Пассивным поворотом будем называть криволинейное движение машины под действием внешних сил без управляющего воздействия со стороны водителя. Исследования пассивного поворота немногочисленны и, как правило, посвящены частным задачам [5, 11, 13], тем более, что они, в отличие от задач управляемого поворота, не всегда имеют однозначное решение.

Наибольший интерес из задач пассивного поворота представляют задачи страгивания и увода.

Под страгиванием в теории поворота понимается начало или конец движения, когда угловая скорость машины равна нулю [1]. Решение этой задачи позволяет определить тягово-сцепные качества машины при сдвиге ее внешней силой, а также возможные угловые ускорения для определения динамических нагрузок в самой конструкции машины [1].

Задача страгивания (сдвига) с изотропным и анизотропным трением была сформулирована и решена еще Ф.А. Опейко [И] на основе трудов Н.П. Шиллера и Н.Е. Жуковского о равновесии площадки с трением [6, 16]. Независимо от значения углового ускорения, для каждой линии действия сдвигающей силы задача страгивания имеет единственное решение относительно величины предельной силы и координат центра вращения.

Теоретические и экспериментальные исследования [2, 17] показали, что на деформируемом грунте задача страгивания гусеничной машины с места решается так же, как на твёрдом. Коэффициенты анизотропного трения в этом случае принимаются равными максимальным значениям продольных и поперечных коэффициентов сцепления гусеницы с грунтом.

Таким образом, задача страгивания гусеничной машины с места под действием внешней сдвигающей силы достаточно полно исследована, имеет теоретическое обоснование и экспериментальную проверку. Страгивание движущейся машины под действием внешней внецентренно приложенной нагрузки имеет некоторые особенности и является началом увода.

Уводом называется отклонение машины от заданного курса. Оценивается увод величиной отклонения, определяемого в результате построения траектории движения. Последняя формируется, как правило, в результате решения дифференциальных уравнений. Однако, для тихоходных машин, когда центробежные силы инерции малы, внешняя сила и силы от грунта можно считать уравновешенными, радиус кривизны траектории в этом случае изменяется крайне медленно, тогда общий случай нестационарного поворота можно рассматривать как квазистатический процесс.

Задача увода тихоходной гусеничной машины под действием внешней внецентренно приложенной силы на твёрдом основании с постоянными составляющими коэффициента трения решается однозначно только как задача страгивания с места. Если внешняя сила не превышает предельного значения для заданной линии её действия, машина движется прямолинейно без отклонения, в противном случае задача не имеет однозначного решения.

Позин Б.М., Трояновская И.П., Апанасик В.Г. Задачи пассивного поворота гусеничной машины______________________________________________________________(постановка, модель движения)

На деформируемом грунте задача увода решается однозначно. Рассмотрим эту задачу подробнее.

Для построения траектории увода в прямоугольной декартовой системе XY воспользуемся теорией криволинейного интеграла первого рода [15]:

Х = Х0 + j cos yds,                                                                 (1)

(s)

Y = Yo + Jsin \|/ds,                                                                            (2)

(S)

где \|/ - угол касательной к кривой в точке с осью X; ds - дифференциал дуги кривой в точке;

Хо, Yo - начальные координаты кривой.

Дуга S через радиус кривизны р и угол касательной у выражается соотношением:

ds = pd\|/.                                                                                                (3)

Таким образом, если известны р и w как функции какого либо параметра, то траектория может быть построена. В качестве параметра, при изучении движения, обычно принимают время т .

* V

Учитывая, что ds = Vdx и V = J ~ dx, формулы (1) и (2) при нулевых начальных условиях о Р запишутся в виде:

X = JVcos J—dx dt, Vo Р )

о

Y = jVsin J—dxldt,                                                               (5)

0 Vo P )

где t, T - время текущее и время процесса, соответственно.

Пусть гусеничная машина под действием внешней силы отклоняется от прямолинейного пути (рис. 1). При равных теоретических скоростях движения гусениц центры скольжения их опорных площадок совпадают (точка С на рис. 1). Радиус кривизны траектории точки С равен рс = хО+х (рис. 2). Таким образом, задача построения траектории сводится к нахождению величин хО и х в подвижной системе координат, связанной с машиной.

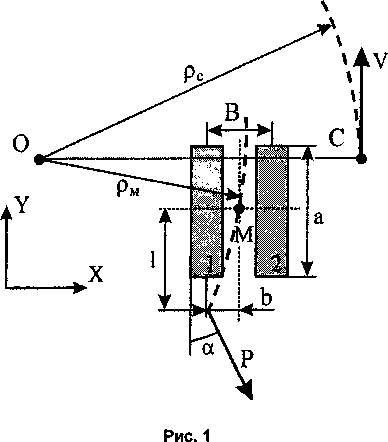
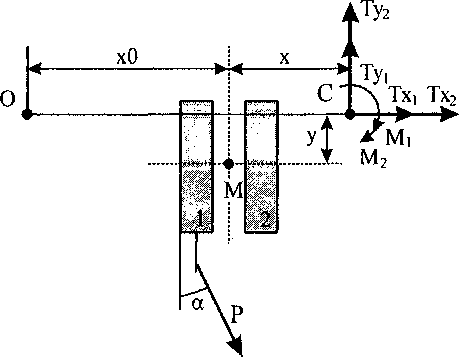
Рис. 2

Значения хО и х легко вычисляются при решении задачи страгивания, записанной в форме условий равновесия машины в различные моменты времени:

Psina + Тх, + Тх2 = 0;

' -Pcosa + Ту, + Ту2 = 0;

lPsina + bPcosa + x(Ty, +Ту2)-у(Тх, +Тх2)-М, -М2 =0.

Расчет и конструирование __________________________________

Входящие в уравнения силовые факторы, возникающие в контакте с грунтом, являются функциями координаты х [11] и учитывают деформативные свойства грунта. В связи с незначительной по сравнению с длиной, шириной гусеницы, последней, как правило, пренебрегают, что позволяет заменить двумерный интеграл при вычислении силовых факторов одномерным [12].

В таком случае силовые факторы, входящие в уравнения равновесия и приведенные к центру скольжения С (см. рис. 2) имеют вид:

0,5а

Тх1>2=- J Цф.

-0,5а

0,5а

ТУ1,2= J q

-0,5а

у-п , х I, „   'V ^’

W-n) +(х±0,5В)

х±0,5В,

,"-7=============^^’

°? (у-^^+^±0,56)^

М₁₂ = q—^у dq, ’ -0,5а ^G”¹!)² +(х±0,5В)²

где знак «+» соответствует отстающей гусенице (Тх,, Ту]3 Mj), а знак «-» - забегающей (Тх2, Ту2, М2); q, фх, фу - удельное давление, коэффициент сцепления в поперечном и продоль ном направлении гусеницы в точке, соответственно.

Поскольку все характеристики взаимодействия движителя с грунтом вводятся в точке, то автоматически учитывается форма и размеры самой площадки и закон распределения удельного давления.

Учёт деформативных свойств грунта в силах взаимодействия (7) производится путем использования переменных коэффициентов сцепления срх, <р . В теории активного поворота гусеничных машин при описании взаимодействия ходового аппарата с грунтом применяются разного рода зависимости, из которых наибольшее распространение в настоящее время получили формулы В.В. Кацыгина [9]:

Ф = фл (1 +---------)th(S5 / X).

1          ch(S8/X)7 v 5 7

где фд - коэффициент сцепления при полном скольжении; S5 - перемещение точки гусеницы; %, X - характеристики грунта.

Формула (8) используется, как правило, при описании установившегося поворота, т.к. её применение требует знания предыстории движения. Этот недостаток можно устранить, используя вместо перемещения S5 в качестве аргумента скольжение в точке к8 [4] (рис. 3):

Ф = ФД(1 +         )th(k5/X).                                                          (9)

ch(k8/X)

Скольжение в точке опорной площадки колеса определяется как отношение скорости скольжения этой точки по грунту к теоретической скорости колеса. Распространим эту' формулу для описания движения гусеницы.

Еще одной особенностью задачи увода являются малые боковые перемещения и скорости. Если при управляемом повороте боковые перемещения точек опорной площадки гусеницы, и связанные с ними деформации грунта, а также скорости относительного скольжения измеряются, соответственно, метрами и м/с, тогда как при уводе - миллиметрами и мм/с. Следовательно, при уводе мы находимся всегда на восходящей ветви коэффициента сцепления (см. рис.З), что позволяет воспользоваться упрощённой формулой [4]:

Ф = ФДФ^. (Ю)

Кроме того, имеет место некоторая неопределённость зависимости силы от скольжения в начальный момент движения или, строго говоря, ненулевого значения силы при нулевом скольжении (см. рис.З). Этот факт широко известен и отмечался еще в опытах В.П. Запольского [8], на базе которых получены формулы В.В. Кацыгина. Обычно это явление учитывается поправками или функциями с некоторыми специальными аналитическими свойствами [10].

Позин Б.М., Трояновская И.П., Апанасик В.Г. Задачи пассивного поворота гусеничной машины (постановка, модель движения)

Сохраняя структуру формулы (10), учтем описанное выше явление, введя в аргумент в качестве слагаемого дополнительный член 6, величина которого равна напряжению в грунте, соответствующему началу сдвига:

Силовые факторы (7) с учетом изложенного выше, имеют вид:

0,5а

Тх,,2=- J qv:

-0,5а

0,5а

'у-ц)2+(х±0,5В)2

ТУ1,₂= J чф_у

х ± 0,5В

7(у-лУ+(х±О,5В)2

(х0 + х)Х

Подставляя (12) в систему уравнений (6), получим квазистатическую модель криволинейного движения при уводе. Из решения системы (6) для каждого значения сдвигающей внешней силы Р(т) находим координаты центра скольжения гусениц х и радиус поворота хО, что позволяет при заданных начальных условиях построить траекторию движения машины, вычислив интегралы (1) и (2).

При дискретном задании времени получаемый в результате решения системы (6) радиус кривизны траектории, а также V можно аппроксимировать любой удобной функцией.