Задачи, приводящие к возмущениям
Автор: Акматов Абдилазиз Алиевич, Шакиров Кылычбек Курбанбекович, Камбарова Айсалкын Даминовна
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Физико-математические науки
Статья в выпуске: 12 т.8, 2022 года.
Бесплатный доступ
В работе исследуется решение однородных сингулярно возмущенных дифференциальных уравнений с начальными условиями. Здесь выполняются условия устойчивости. В качестве начальной точки возьмем точки смены устойчивости. В окрестности этой точки появится пограничный слой, которые изучаем с помощью метода регуляризации. Особенность и новизна работы заключается в том, что здесь применен метод регуляризации к исследованию решений сингулярно возмущенной задачи.
Устойчивость, регулярные и сингулярные возмущения, начальная точка, решение, биустойчивость, дифференциальные уравнения, бесконечно малые величины, малый параметр, коэффициент пропорциональности
Короткий адрес: https://sciup.org/14126019
IDR: 14126019 | УДК: 517.928 | DOI: 10.33619/2414-2948/85/03
Текст научной статьи Задачи, приводящие к возмущениям
Бюллетень науки и практики / Bulletin of Science and Practice
В работе рассматривается задачи приводящие к регулярным и сингулярным возмущениям. Для простоты рассмотрим случаи, когда математические модели были однородные дифференциальные уравнения первого порядка. Когда рассмотрим, задачи по возмущениям значительную роль играет, условия устойчивости. Поэтому мы в работе тоже рассмотрим устойчивости решений дифференциальных уравнений [1–6].
Учитывая, что малый параметр £ является безразмерной величиной, составим математическую модели некоторых задач. В первом примере покажем, условия устойчивости и асимптотические близости решений возмущенной и невозмущенной задачи. Во втором примере, что коэффициент пропорциональности определяют типы возмущений. Третьем примере, исследуем решение дифференциальных уравнений имеющая регулярные и сингулярные возмущение. Приводим примеры.
Задача однородная, исследование ведется в действительной области.
Цель исследования. В работе рассматриваются начальная задача Коши в регулярной области. Цель исследования — показать асимптотическую близость решений возмущенной и невозмущенной задачи.
Материалы и методы исследования
Рассмотрим dy(t, £)
£ X —— = a(t)y(t, £) dt
y(t,£) = y0, на полуоси [0, + да).
Уравнения (1) называется устойчивым (точнее, устойчивым вправо), если его решение ограничено на [0, + да ).
Решения уравнения (1), (2)
y(t, £) = y0 exp (-^ a(s)ds)
Формально взяв £ = 0 получим невозмущенные уравнения
a(t)y (t, £) = 0.
Если a(t) Ф 0 имеем решение
y(t,0) = 0.
Нули или полюсы функции a(t) определяют бисингулярность возмущенного уравнения (1). В этих точках появится пограничный слой, способы решения показаны в работе [7]. В общем случае, сингулярно возмущенные дифференциальные уравнения (1) называется бисингулярной однородным дифференциальным уравнением.
Невозмущенные уравнения алгебраической, поэтому оно не сможет удовлетворить начальному условию (2).
Пусть в области [0, + да ) решения уравнения (1) является устойчиво вправо. Тогда в окрестности точки t =0 появиться пограничный слой. Толщина пограничного слоя можно определить [7] и оценить используя методы которые изложены в этой работе. Но мы используем иные способы получение оценки [2] которые называются методом регуляризации решений.
Рассматриваемую область, делим следующим образом: t Е [-ап(£); ап(£)], где ап(£) ^ 0 , £ ^ 0 , и £ = о(ап(£)) , п Е N , а также t Е [ап(£), + да ) — которую можно называть устойчивой или регулярной областью [7].
Если рассмотрим область tЕ[ап(£),+ да) , то выполняются условия устойчивости вправо, поэтому решения задачи (1), (2) стремится к нулю по порядке £:
I y ( t , e )| <
t
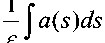
\
,
где t o = 0.
Выполняется предельный переход или решение (6) стремится к равенству (5)
/im|y(t,£)| =y(t,0), tE [an(£),+ да ).
£^0
В пограничном области t E [—ап(г),ап(г)\ , nEN решения (1), (2) применим метод регуляризации, которые отличаются от метода, которые использованы в работе [7]. Для этого составим функционал
(y(t, е),^))
ante) 1 t
= I exp I a(s)ds x y(s)ds
-ante) Е t o
Здесь функция y(t) — финитная функция
^(t)={exp(
^ П (^) аП^ — t 2
,t E [~а п (Е),а п (Е)],
0,t^ [-а п (Е),а п (£)].
Из (7) по модулю
|(y(t,£),^(t))| = lfttoexp( 1 ft T oa(s)ds) x ^(r)drl = fO^^exp ( ^ Re £ a(s')ds') x y(r)dr.
К последнему равенству применим теорема о среднем [8]
I(y(t,s),^(t))1 = |fttoexp( 1 ftToa(s)ds) x y(r)dr| = y^f-^^exp ( 1 Re f*^
Учитывая, что в области t E [—ап(г),ап(г)\, функция -ап(г) < Re f t a(s)ds < ап(е) t 0
тогда
t
l(y(t,E),y(t))l = || exp (-^ a(s)ds) x y(r)drl = y(0) ^
Jto \£ J t0 / —
o
o
ante)
exp
-a n ( £)
tel
a(s)ds) dr <
< Ф(0) f^ di = 2а п (гЫ0). a n (t)
Получим оценку ly(t,E)1 < (^ап(г) (8)
где ( — постоянные числа, ап(£) ^0, £ ^ 0 и £ = о(ап(е)), nEN.
Из (6), (8) видно для решения (3) имеет место оценка
( (£,t E [а п (£),+ да ),
I ёа п (Е),г E [-а п (£),а п (£)\.
Близость решений возмущенной и невозмущенной задачи зависит от пограничного слоя. Из (9) видно, что выполняется предельный переход решений (1), (2) и (4).
Рассмотрим примеры. 1) Пусть a(t) = —t , функция неустойчиво в интервале t E (— да, 0) , устойчива t E (0, + да) , t = 0 — точки перехода от неустойчивой к устойчивому
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №12. 2022 интервалу. В качестве начальной точку рассматривается в области t Е [0; + ю) . рассматриваемой области. Из (3) имеем
возьмем t = 0 тогда решения задачи (1), (2)
Решения задачи (1), (2) устойчиво вправо в
y(t, г) = у0 ехр (- J (-s)ds)
= у0 ехр (- ^ .
В области t Е [Ve, + ю ) имеем оценку
|y(t,£)| < Сг.
Если t Е [-Ve, Ve], то имеет место оценка
|y(t,£)| < CJF.
Учитывая полученные оценки (11), (12) для решения (10) получим оценку
|y(t,£)| =
(Ce,t Е [VC, + ю ), {eve, t е [о, ve).
Из равенстве (13) видно, что предельный переход возмущенной и невозмущенной задачи выполняется в области t Е [0; + ю ).
-
2) Найти закон изменения яркости света после прохождения через стеклянную пластину, если при прохождении через слой толщиной x 1 =2,5 мм яркость света B 1 составила 30 межд. ед. (Рисунок). Лучи падают на поверхность пластины под любым углом, а его изменение отражается на величине коэффициента k .
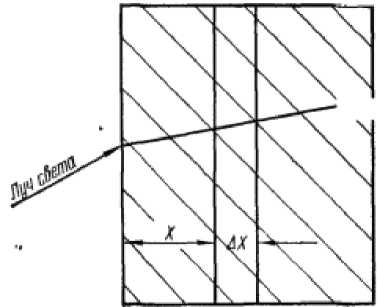
Рисунок.
Решение. Величина яркости света B , пропускаемого стеклянной пластиной, изменяется в зависимости от толщины пластины. Часть световой энергии поглощается стеклом, и сила света уменьшается. Так как яркость света зависит от толщины пластины, то силу света I будем рассматривать как функцию толщины x , т. е. I=I(x) . Если при толщине стеклянной пластины x мм сила света I межд. ед., то при увеличении толщины пластины на величину Δx получим уменьшение яркости света.
Пусть сила света на участке Δx уменьшается равномерно. Тогда условное уменьшение яркости после прохождения через слой толщиной Δx можно определить di = -Шх (14)
Где k — коэффициент пропорциональности, Δx=dx. Знак минус указывает на уменьшение яркости с утолщением стеклянной пластины.
Из дифференциального уравнения (14) после разделения переменных находим у = —kdx,
Откуда после интегрирования получаем
Ini = —kx + C.
Начальное условие: при x 0 =0, I 0 =100. Отсюда, согласно уравнению (15),
In100 = —kx0 + C,
и
C = In 100.
Подставляя найденное значение C в общее решение (15), получаем Ini = —kx + Ini 00, тогда
i
^n—— = 100
—kx
Дополнительное условие: при x 1 =2,5, I 1 =30, дает равенство
In— = —2,5k,
Откуда коэффициент пропорциональности
k = —2ln0,3 = 0,481.
Найденное значение коэффициента пропорциональности (17) подставляем в равенства
(16), после чего искомый закон принимает вид
i
In =
—0,481x
или i = 100e-0,481x
Из равенство (16) видно что, коэффициент пропорциональности k зависит от толщины стеклянной пластины т. е. переменной x . Если толщина пластины 0 < x < 3,4, то возмущения будет регулярной, если 3,4 < x < + да то возмущения будет сингулярной.
Вышеуказанном примерам видно, что типы возмущений также зависит от коэффициента пропорциональности. В свою очередь коэффициент пропорциональности — это безразмерная величина.
-
3) Моторная лодка движется в спокойной воде со скоростью d0 = 20 км/час. Течение воды постепенно увеличивается и направляется против направления лодки. Составьте уравнению и исследуйте решению.
Решение. На движущуюся лодку действует сила F = —kd , где к — коэффициент пропорциональности. По закону Ньютона сила равна произведению массы на ускорение
F
dd
= тх — dt
Откуда дифференциальное уравнение движения
тх — = —kd dt
С увеличением течение увеличивается коэффициент пропорциональности. Наивысшие коэффициент пропорциональности соответствует к большим, а наименьшим к медленным течением. В обоих случаях коэффициент пропорциональности не равен нулю или бесконечности.
Здесь масса m — постоянная, но размерная величина. Уравнения (18) является однородным дифференциальным уравнениям первого порядка.
Начальная условия: при t=0, d0 = 20 км/час. Если течение воды спокойная или малая то коэффициент пропорциональности k определяет регулярную возмущению. Противном случае с резким увеличением лодки определяет сингулярную возмущению.
Рассмотрим обе случаи. Пусть коэффициент пропорциональности определяет регулярную возмущению. Тогда из уравнения (18), формально взяв k=0 получаем невозмущенную уравнению dd(t) _ (19)
dt
С начальным условием
d(0) = 20 км/час. (20)
Решением уравнения (19)
Kt) = C+d0.
В этом случае со временем лодка сохраняет постоянную скорость. Учитывая условие (20)
d(t) = 20 км/час.
Решение (18) с условием (20)
d(t) = 20 exp (-k-t).
Предельный переход выполняется limd(t) = Kj)
k^0
Пусть 0 < к < + да. В этом случае уравнения (18) записываем в виде dd(t) d(t)(24)
-
8 X-----=--
- dtm
где 8 = 1 , 0 < 8 <1.
k
Формально взяв, 8 = 0 имеем невозмущенную уравнению
^(t) = 0.
Уравнения (25) является алгебраическим и не удовлетворяет начальному условию (20).
Основная задача показать асимптотическую близости решений сингулярно возмущенной и невозмущенной задачи, т. е. предельный переход limd(t) = ti(t).
£^0
d(t) = 20 exp (--^t).
Предельный переход решений (18) и (25) выполняется и решения устойчиво вправо.
Поэтому верна оценка (9) в области t Е [0, + ж ).
Результаты и обсуждение
Показано асимптотические близости решений возмущенной и невозмущенной задач. Приведены несколько примеров. Каждый из них иллюстрирует определенные особенности возмущений. Например, в первом примере конкретном значении функции a(t) сущность возмущенной задачи. Во втором примере показано, что в качестве малого параметра можно взять коэффициент пропорциональности. Последнем примере рассмотрено задача приводящие к устойчивости. Заметим, что устойчивость вправо одним из частных случаи биустойчивости.
Показаны методы получения оценки решений возмущенной задачи. Этот метод называется методом регуляризации решений.
Вывод
Задача однородная, поэтому исследования проводились в действительной области. Оценка пограничного слоя получилась с помощью метода регуляризации решений [2]. Новизна статьи — это применение метода регуляризации к пограничного слоя и приведенные прикладные примеры.
Список литературы Задачи, приводящие к возмущениям
- Акматов А. А. Метод регуляризации решений бисингулярно возмущенной задачи в пространстве обобщенных функций // Бюллетень науки и практики. 2022. Т. 8. №2. С. 10-17.
- Акматов А. А. Асимптотика решений однородного бисингулярно возмущенного дифференциального уравнения в теории обобщенных функций // Бюллетень науки и практики. 2022. Т. 8. No2. С. 18-25.
- Акматов А. А. Комплекстик тегиздикте френель интегралдарынын асимптотикалык ажыралмасы // Вестник ошского государственного университета. 2021. Т. 3. №1. С. 19-26.
- Акматов А. А. Сингулярдык козголгон маселенин чечимин изилдөө // Вестник ошского государственного университета. 2021. Т. 3. №1. С. 26-33.
- Барбашин Е. А. О построении функций Ляпунова // Дифференциальные уравнения. 1968. Т. 4. №12. С. 2127-2158.
- Каримов С., Акматов А. А. Исследование решений системы сингулярно возмущенных дифференциальных уравнений, когда собственные значения матрицы имеют мнимые части // Вестник Ошского государственного университета. 2021. Т. 1. № 1. С. 61-70.
- Тампагаров К. Б. Погранслойные линии в теории сингулярно возмущенных обыкновенных дифференциальных уравнений с аналитическими функциями: Дисс. … д-р физ.-мат. наук. Жалал-Абад. 2017. С. 180-280.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. М., 2016. С. 120-126.


