Задание скорости вытягивания при выращивании монокристаллов германия

Управление скоростью вытягивания кристалла V (х) в микропроцессорных установках вытягивания монокристаллов германия, внедренных на базе патента [1] на ФГУП «Германий», производится на основе выражения

V . ( x ) = V _n,₃ ( x ) + ZKv A y , (1) где K^ - пропорциональный коэффициент регулирования по скорости; V (х) - программное задание закона изменения скорости; Z- признак управления по диаметру на цилиндрической части кристалла.

Программное задание изменения скорости V (х) в микропроцессорных системах выращивания германия задается технологом за счет ввода в управляющую ЭВМ 24-кадровой системы управления параметрами вытягивания. После выращивания первых образцов заданной марки кристалла программное задание скорости корректируется на ЭВМ на основе анализа записи.

От закона изменения скорости вытягивания кристалла зависит получение заданной формы фронта кристаллизации вдоль оси кристалла (близкой к плоскому), что является актуальным для монокристаллов германия кристаллографического направления «100» и связано с получением нужной структуры и качества готовых слитков. Ниже приводятся математические выражения для формирования закона изменения скорости вытягивания V (х), которые позволяют автоматизировать процесс ввода задания скорости в систему управления установкой.

Совместный анализ уравнения [2], которое приравнивает вес массы столбика расплава (высотой h) силам поверхностного натяжения, действующим по окружности (для кристалла диаметром d), и выражения [3] высоты столбика расплава через уравнение теплового баланса на фронте кристаллизации, дает математическую зависимость величины среднего перегрева расплава X относительно температуры кристаллизации материала в виде выражения

X= C t L - CV .            (2)

d где Cv =рж —; Ct = 4; X = (T-T); И-ско-

Лтв        рж Хж g рость вытягивания кристалла; Тк - температура кристаллизации материала; Т- температура расплава в зоне фронта кристаллизации;L - линейный осевой градиент в твердом кристалле; Е - удельная теплота плавления материала; X - коэффициент теплопроводности расплава; Хтв - коэффициент теплопроводности кристалла; g - ускорение свободного падения; r - радиус столба расплава; о - поверхностное натяжение расплава; р - удельная плотность жидкого материала.

Величина среднего перегрева расплава X для германия лежит в пределах 0,2...2 °С. В общем случае средний перегрев X , согласно выражению (2), есть функция осевого градиента в кристалле L и скорости вытягивания кристалла V.

Рассмотрим процесс управления основными параметрами выращивания кристалла (рис. 1). Используя линейную аппроксимацию параметров на узловых участках выращивания кристалла, можно получить следующие выражения для определения задания скорости вытягива ния V (х) на конусной, цилиндрической части кристалла п.з и при формировании обратного конуса соответственно:

Vn.3 (x) = Vo - x [V0  V1], x1

Вестник Сибирского государственного а >рокосмического университета имени академика М. Ф. Решетнева

(x - x У - V

V з ( x ) = V —    ,       , ,            (4)

( ^x 2 ^{- x} 1 )

V„ ( x ) = V ^/: / ^:| ' V ,        (5)

( ^x 3 ^{- x} 2 )

где У₀ - начальная скорость вытягивания кристалла при включении режима «автомат»; У - скорость вытягивания кристалла при завершении формирования обратного конуса; У₂- скорость вытягивания кристалла при завершении формирования цилиндра; У₃- скорость вытягивания кристалла при завершении формирования обратного конуса; X j - завершение формирования прямого конуса кристалла; х₂- завершение формирования цилиндрической части кристалла; х₃ - завершение формирования обратного конуса кристалла; х - координата перемещения кристалла.

V 3 ^-

X d о р з

L1          ,

где L₀- осевой градиент в начале цилиндрической части кристалла; L₁ - осевой градиент в конце цилиндрической части кристалла; У_о, У₁, У₂, У₃ - узловые точки скорости вытягивания; d₀- диаметр вытягиваемой шейки кристалла; d - диаметр цилиндрической части кристалла.

Технологические поправочные коэффициенты Р. вводят ся для возможности корректировки скорости вытягивания, исходя из технологических требований (например, равномер ности легирования кристалла по его длине, при допущении некоторой величины прогиба фронта кристаллизации).

По выражению (6) построим область допустимых значений выбора скорости вытягивания для германия (скорость должна находиться в положительной области) (рис. 2).

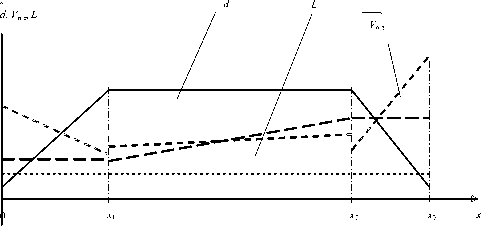
Рис. 1. График задания параметров процесса выращивания монокристаллов: d - задание диаметра выращиваемого монокристалла; У_пз - задание скорости вытягивания;

L - задание осевого градиента; х - ось кристалла;

х1 - координата завершения формирования прямого конуса кристалла; х2 - координата завершения формирования цилиндрической части кристалла; х3- координата завершения формирования обратного конуса кристалла

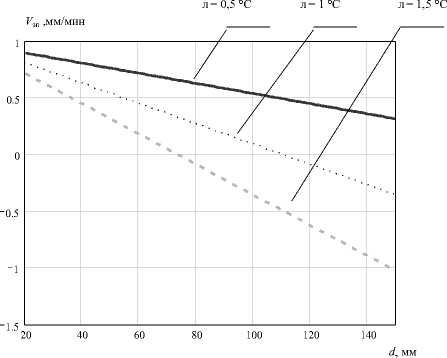
Рис. 2. Графики допустимой скорости вытягивания германия при осевом градиенте L = 20 °С/см

Для автоматического определения значений координат скорости вытягивания в узловых точках (У_о, У, У₂, У₃) преобразуем выражение (2), введя технологические поправочные коэффициенты Р _; :

V з ( d ) =

X d р i

Таким образом, разработанная математическая модель задания скорости на установке выращивания монокристаллов германия при контактном методе измерения и управления текущей площадью кристалла позволяет автоматизировать процесс ввода задания скорости в систему управления и сокращает цикл изготовления готовой продукции требуемого качества.

где У/d) - скорость вытягивания кристалла; d- диаметр кристалла; р . - технологические коэффициенты снижения скорости (0,9...0,2).

Из выражения (6) для узловых точек скорости вытягивания получим:

V - Т ^X d 0 Ро V O ^- L 0 ^-       ,.

v _Т Xd P i V 1 - L 0 , ,

V _ j Xd в2 V 2 = L1 .    ,