Задание температуры при выращивании монокристаллов германия

Рассмотрена математическая модель задания температуры на установке выращивания монокристаллов германия по способу Чохралъского, позволяющая автоматизировать процесс ввода программного задания температуры в микропроцессорную систему управления установкой.

В основу контактного метода измерения и управления выращиванием монокристаллов [1-5] по способу Чохральского входит управление текущей площадью (или диаметром при круглой форме) растущего кристалла на основе вычисления сигнала управления Д у как функции отклонения текущей площади кристалла от заданной, на базе вычисленных перемещений кристалла и тигля за период оценки сигнала управления Т_ц. Управление температурой боковой поверхности нагревателя Т (х) в микропроцессорных установках вытягивания монокристаллов германия, внедренных на базе патента [1] на ФГУП «Германий», производится на основе выражения

Т з ( x ) = T _n,₃ ( x ) + ZA_T /Д ydx ,           (1)

где А_Т - интегральный коэффициент регулирования по температуре; Т (х) - программное задание закона изменения температуры; Z - признак управления по диаметру на цилиндрической части кристалла; х - перемещение вдоль оси кристалла; Д у - сигнал управления.

Программное задание закона изменения температуры Т (х) в микропроцессорных системах выращивания германия задается технологом за счет ввода в программу управления 24-кадровой системы управления параметрами вытягивания. После выращивания первых образцов заданной марки кристалла, введенный выше программный закон изменения температуры корректируется на ЭВМ на основе анализа записи. При производстве

кристаллов германия удовлетворительным получается

процесс корректировки программного закона изменения температуры Т (х) после выращивания от четырех до пяти кристаллов заданной марки: Ниже приводятся математические выражения для формирования программного задания температуры нагревателя Т (х), которые позволяют автоматизировать данный процесс.

Совместный анализ уравнения [6], которое приравнивает вес массы столбика расплава (высотой К) силам поверхностного натяжения, действующим по окружности (для кристалла диаметром d), и выражения [7] высоты столбика расплава через уравнение теплового баланса на фронте кристаллизации, дает зависимость диаметра кристалла d от скорости вытягивания Г и температуры расплава Т в виде выражения

d = Ct

^[ L ^- C V • V 3 ] [ T - Тк ] ,

E где CV =рж —;

^ тв

C t = 4

°^ тв

р X g ж. ж.

; Г - скорость вытяги-

вания кристалла; Т - температура кристаллизации материала; Т- температура расплава в зоне фронта кристаллизации; L - линейный осевой градиент в твердом крис-

талле; Е - удельная теплота плавления материала; Х _ж -коэффициент теплопроводности расплава; X - коэффициент теплопроводности кристалла; g - ускорение свободного падения; г - радиус столба расплава; о - поверхностное натяжение расплава; р - удельная плотность жидкого материала.

На установках вытягивания монокристаллов германия на ФГУП «Германий» в контуре регулирования температуры применяется датчик с сапфировым светопроводом, который проецирует часть излучения с боковой поверхности нагревателя на радиационный пирометр, а в качестве программно управляемого регулятора температуры используется прецизионный регулятор температуры РИФ-101. В работе [8] подчеркнуто, что регулирование температуры расплава германия на основе датчика с сапфировым светопроводом производится не в абсолютной, а в относительной температуре на основе ЭДС радиационного пирометра в мкВ.

Для того чтобы в выражении (2) перейти к программируемой температуре Т (х) в мкВ, в установившемся режиме на цилиндрический части выращиваемого кристалла примем за основу линейную модель связи температуры расплава Т с температурой боковой поверхности нагревателя Т (х):

ТП З(х) = Т (x) Km,

.

Тм = Тк Km,(4)

т

Km =    ,(

^Т к где К_т - линейный коэффициент преобразования регулятора температуры; Т - температура боковой поверхности нагревателя, соответствующаятемпературе кристаллизации материала .

Объединяя выражения (2-5), получим выражение для управления нагревателем:

Т _П,3 ( X ) = Т к K m + C t K m ^[L - C V   ⁽ x ^{) ]} ,       (6)

d ₃ ( x )

где dз(х) - программное задание выращиваемого диаметра кристалла; Г (х) - программное задание скорости вытягивания кристалла.

Рассмотрим процесс управления основными параметрами выращивания монокристалла германия (рис. 1). Используя линейную аппроксимацию параметров на узловых участках выращивания кристалла, можно получить выражения для вычисления данных параметров микропроцессорной системой управления на всех участках выращивания.

Выражения по заданию диаметра d_з(х) и температуры Т (х) на прямом конусе кристалла примут вид: п.з

d ₃ ( x ) = d о + x ^[ d i d ^{0 ]} , ^x 1

T n.3 ( X ) = T K K m + C t K m

[ L - C V • V n.3 ^{( X ) ]}

x [ d i - d о ]

d 0 + —

L          xi     J где x - координата перемещения кристалла; Xj - координата завершения формирования прямого конуса кристалла; L0 - величина осевого градиента в кристалле на конусной части; d0- диаметр вытягиваемой шейки кристалла; d- диаметр цилиндрической части кристалла.

Выражения по заданию диаметра d (х) кристалла и температуры Т_пз(х) на цилиндрической части кристалла примут вид:

d ₃ ( x ) = di ,

T n.3 ( X ) = T k K m + C t K m

L 0 + [ x ^{- X} 1 ]       °t ^- C V V n.3 ^{( x} )

_: ( ^x 2 ^{- X} 1 ) _:

di где x2 - координата завершения формирования цилиндрической части кристалла; L1- осевой градиент в кристалле в конце цилиндрической части.

Выражения по заданию диаметра d (х) кристалла и температуры Т (х) на обратном конусе примут вид:

п.з d3(X) = di-(x-X2)[di -d0] (x3 - x 2 )

T n.3 ( X ) = T K K m + C t K m

[ L i - C V V n.3 ( X ) ] d    ( ^{X - X} 2 )[ d i ^{- d} 0 ]

. ‘       ( ^X з ^{- X} 2 )

где x3 - координата завершения формирования обратно го конуса кристалла.

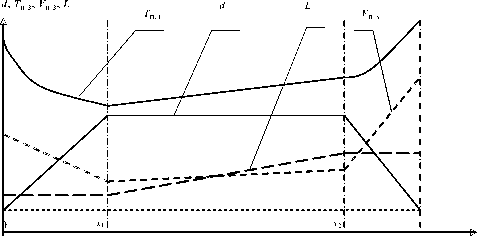
Рис. 1. График задания параметров процесса выращивания монокристаллов: d - задание диаметра выращиваемого монокристалла; Т_{п з} - программное задание закона изменения температуры; L - задание осевого градиента;

х - перемещение кристалла; х1 - координата завершения формирования прямого конуса кристалла; х2 - координата завершения формирования цилиндрической части кристалла; х3 - координата завершения формирования обратного конуса кристалла; V - программное задание закона изменения п.з скорости вытягивания

График изменения температуры боковой поверхности нагревателя Тз (T_sum) на работающей установке с вводом задания температуры по вышеприведенной модели приведен на рис. 2.

Моделирование программы задания температуры позволило без процесса предварительного вытягивания монокристалла в ручном режиме ввести задание температуры в систему управления установкой, что значительно сократило цикл изготовления готовой продукции. При автоматическом вводе расчетного задания температуры в микропроцессорную систему управления технологу остается функция корректировки трех коэффициентов процесса К_т, L₀ и L₁, по результатам вытягивания предыдущего кристалла.

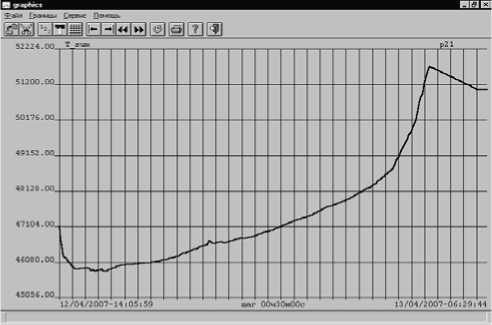
Рис. 2. График изменения температуры нагревателя Тз (T_sum)

Итак, разработана математическая модель задания температуры на установке выращивания монокристаллов германия при контактном методе измерения и управления текущей площадью кристалла. Данная модель позволяет при изготовлении готовой продукции автоматизировать процесс ввода программного задания температуры в систему управления установкой, что значительно сокращает время отработки закона управления температурой.