Закон Малюса в квантовой электродинамике

Закон Малюса экспериментально был установлен французским физиком Э.Л. Малюсом в 1810 году, который будучи сторонником корпускулярной теории света Ньютона, пытался объяснить его с помощью движущихся световых частиц. Однако состояние физической науки в то время не позволило это сделать. Закон Ма-люса связывает интенсивность I линейно поляризованного света, вышедшего из анализатора, с интенсивностью I ₀ линейно поляризованного света, падающего на анализатор:

I = 1 0 cos² 0 , (1) где 0 — угол между плоскостями поляризации падающего и вышедшего света.

Обычно запись закона (1) сопровождается замечанием, что поглощение света не учитывается, или в формулу (1) напрямую вводят некоторый коэффициент прозрачности вещества анализатора.

Вывод закона Малюса на основе волновой теории света абсолютно тривиален [1], и мы не будем на нем останавливаться. Однако результат этого вывода (1) обладает одним существенным недостатком. Дело в том, что давление света, т. е. создание продольного по направлению светового вектора импульса у рассеивающей частицы (атом, ион, молекула и т. д.), может быть объяснено как на основе волновой, так и корпускулярной теории света [2]. Под рассеиванием квантов мы будем иметь в виду их переиз-лучение частицей вперед. Однако в формуле (1) полностью отсутствуют какие-либо указания на существование светового давления, несмотря на то, что эта формула отражает процесс взаимодействия световой волны с частицей.

В действительности свет обладает квантовой природой, а квант света – продольным импульсом, который может быть передан частице. Поэтому с точки зрения квантовой теории света формула (1) принципиально неточная.

Представляет интерес найти поправки к формуле (1), обусловленные квантовой природой света. Вычисления будем проводить в рамках теории возмущений.

При выводе формулы (1) предполагается, что световая волна, в частности ее вектор напряженности электрического поля, может разделяться на две составляющие, одна из которых проходит через анализатор, другая через него не проходит.

Квантовая природа света не предполагает возможности разделения кванта света на две части, но квант сначала может поглотиться частицей (которая не должна быть полностью свободной), а затем излучиться с другой частотой и другой плоскостью поляризации. Если плоскость поляризации переизлученного кванта совпадает с плоскостью анализатора, то квант пройдет через анализатор. В противном случае он поглотится анализатором. В процессе переизлучения кванта существенную роль играют вероятностные процессы, т. к. направление плоскости поляризации отдельного переизлученного кванта зависит от множества факторов, в частности от © Волобуев А.Н., 2015

состояния частицы в момент перизлучения, возбуждаемой квантом степени свободы (электронной, колебательной), уровня симметрии строения переизлучающей частицы и т. д.

1. Взаимодействие кванта света с частицей вещества

Рассмотрим модель взаимодействия кванта света с заряженной частицей, например ионом массой m , в результате которого квант света при переизлучении на частице, с одной стороны, изменяет направление своей поляризации на угол @, а с другой стороны, сохраняет направление своего движения (рис. 1).

Вероятность перехода системы «фотон–частица» в единицу времени из начального состояния (до взаимодействия) в конечное (после взаимодействия) пропорциональна квадрату соответствующего матричного элемента взаимодействия H _вз оператора Гамильтона, т. н. «золотое правило Ферми» [3; 4]:

dW = — \Н вз| Pf d " ,                       (2)

где Pf — число конечных состояний системы «фотон–частица» , приходящихся на единичный интервал энергий конечного состояния [5]; d Q — телесный угол, характеризующий направление вылета переизлученного фотона; Й — приведенная постоянная Планка.

Пусть до взаимодействия с частицей импульс фотона был к = И = ^, c где toi — частота фотона; с — скорость света в вакууме. Импульс частицы pi = |pj.

После взаимодействия число конечных состояний переизлученного фотона импульсом k 2 = |k 21 = Й ® 2 / с в объеме V = 1, приходящихся на энергетический интервал фотонов, соответствующий импульсному интервалу dk ₂, равно р dk 2 , где

P       "' 2      = k

( 2л с ) Й ( 2- Й ) с

– число состояний фотонов, приходящихся на единичный интервал их энергий [4]. Естественно, число состояний переизлученных фотонов определит число состояний всей системы [5]:

Pf dE f = с р dk ,                               (3)

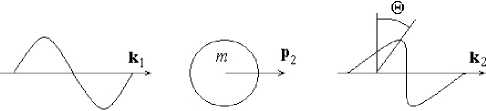
Рис. 1. Модель взаимодействия кванта света с переизлуча^ ющей частицей

где dE _F – энергетический интервал конечного состояния системы, соответствующий импульсному интервалу фотонов dk ₂. Следовательно:

д к

^{P f} = ^{c р} д E F .

Подставляя (4) в (2), найдем вероятность перехода системы «фотон–частица» в единицу времени из начального состояния в конечное:

2л     2   дк dW = H   ср — dQ,                 (5)

Й I ^вз      д E _F     ’

Используя (5), найдем дифференциальное эффективное сечение процесса. Квантово-механическое определение дифференциального эффективного сечения следующее [4; 6]: дифференциальное сечение рассеяния – это отношение числа рассеянных в единицу времени в элемент телесного угла квантов dNрас к плотности потока j0 падающих квантов:

dN d Q = —рас j0

.

Учитывая j o = Nc, где N — объемная концентрация фотонов, падающих на рассеивающую частицу в единицу времени, и полагая объем V = 1, найдем дифференциальное эффективное сечение процесса рассеяния квантов на частице:

dNрас dW d □ =---— =---,

Nc c где учтено dN dW =---рас .

N

Следовательно, дифференциальное эффективное сечение процесса с учетом k2

P =    23-

(2лЙ) с равно:

,     2л 2 дк dG=   H вз P TZ2 d" =

Й        д E f

₌ 2л      ²    k 2 ²     З к 2_

= Й ^H ( 2- Й ) ³ с aE F ^d ".

Производную дк2 / дEf по причинам, которые будут ясны в дальнейшем, найдем позже.

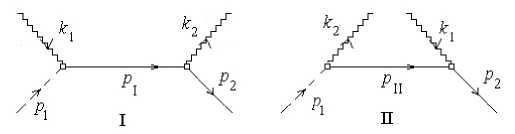
. 12nq2 i k1

Рис. 2. Диаграммы Фейнмана для взаимодействия ««фотон-частица». Модель взаимодействия кванта света с переизлу-чающей частицей

e ₁

– амплитуда вероятности поглощения фотона k ₁

с 4-вектором поляризации e ₁,

. 12nq2 i k2

e ₂

2. Нахождение матричного элемента оператора взаимодействия

Перейдем к нахождению матричного элемента H _вз. Воспользуемся диаграммной техникой Фейнмана [3]. В [7] данная задача решалась без использования диаграммной техники Фейнмана. Для удобства вычислений дальнейшие преобразования проведем в 4-векторной форме. Используем также т. н. рациональную систему единиц, в которой скорость света и постоянная Планка равны единице с = Й = 1. В этой системе единиц

– амплитуда вероятности излучения фотона k ₂ с 4-вектором поляризации e ₂, q – заряд частицы (частица может быть также электронейтраль-ной, что будет учтено далее), и * - амплитуда сопряженной волновой функции частицы. Использовано стандартное обозначение операто- 0

ров a = a y t - a ■ Y, так что оператор a связан с Y-матрицами Дирака.

Матричный элемент для второго пути процес-

са имеет вид

энергия импульс и масса имеют одну и ту же

. 2пq ²  [             1

i ,       1 u ₂ e 1  -----x-------- e ₂ u 1

у] kk [ p 1 - к 2 - m

размерность.

Возможны два пути, по которым может про-

исходить рассеяние фотона на частице (рис. 2).

Путь I: частица, имеющая импульс p ₁ в начальном состоянии с амплитудой волновой функции u ₁ взаимодействует с фотоном, имеющим импульс k ₁, поглощая его, приобретает импульс p I = Р у + к ^ . Затем частица излучает фотон импульсом k ₂ и переходит в конечное состояние с амплитудой волновой функции u ₂ и импульсом p ₂.

Путь II: частица, имеющая импульс p ₁ в начальном состоянии с амплитудой волновой функции u ₁ излучает фотон, имеющий импульс k 2 , приобретая импульс p _п = p 1 - к 2 . Затем частица поглощает фотон импульсом k ₁ и переходит в конечное состояние с амплитудой волновой функции u ₂ и импульсом p ₂.

Матричный элемент для первого пути процесса имеет вид [3]

Традиционно порядок сомножителей, отражающих стадии процесса в матричном элементе, записывается справа налево.

Суммарный матричный элемент процесса взаимодействия «фотон–частица» имеет вид:

2n q   I *           1

H вз = i /, ,  1 u2e 2”    ~ e 1U1 + кк [ p 1 + к 1 - m

. . *                  1

+ U2 e 1 —----x------ p 1 - к 2 - m

e ₂ u ₁

= i

2n q ²

*I 1

U 2 1 e 2 ~----------- e 1 +

[ p 1 + к 1 - m

~         1        ,

+ e 1 "x-----x-------- e 2 r U 1.

p 1 - к 2 - m

Проведем в (10) некоторые преобразования.

i

4п q ² i

2 k ₂

4п q ² i

2 k ₁

X

p 1 + к - m

( j3 1 + Z c 1 + m )

( j3 1 + Z c 1 - m ) ( j 3 1 + Z c 1 + m )

e ₂

p 1 + к 1 — m

e у и -

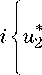
. 2п q ²

—\—~

V ^k 2

( j 3 1 + к 1 + m )    ( j3 1 + к 1 + m )

( j 3 1 + Z c 1 ) - m ^{2       2} ( ^Р1k1 )

e ₂

p 1 + к 1 - m

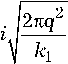
e ₁ u ₁

. 2nq ² [             1

= i ,     < u e ^ -----x------ e и

V k 1 k 2 [ 2 2 Р 1 + к 1 - m ^{1 1}

где

где использованы следующие соотношения для 4-векторов:

p ² = ( pp ) = EE - pp = E ² - |p 2 = m ², т. к.

E ² = |p| ² + m ² и ( кк ) = к 0 к 0 - kk = 0,        (12)

где E - энергия частицы; p - ее 3-вектор импульса; k ⁰ – энергия фотона; k – его 3-вектор импульса. В рациональной системе единиц E = |p| и к ⁰ = |k| . Таким образом:

( P i ⁺ k i ) 2

— m ²

= ( P i P i ) + 2 ( P i k i ) + ( k i k i ) — mm

P + m

R =------,

2 E

= m ² + 2 ( p i k i ) + 0

—

m ²

= ² ( P i k i ) .

так что

Аналогично:

^^

^^

p ₁

—

k ₂

—

m

( p i ^{— k} 2

( P i — k 2 + m )

—

m ) ( p 3 i — k 2 + m )

_ ( P i — k 2 + m ) _

^   2

(pi — k2 )

—

m ²

поскольку

( P i ^{— k} 2 ) 2

— m ²

Следовательно,

виду

-^

H

вз

= i

2n q ²

*

^— e i

= i

x

—

( P i — k + m )

² ( P i k 2 )     ’

^{— 2} ( P i k 2 ) .

формула (10) преобразуется к

k ₁ k ₂

u ₂

e ₂

( p + k + m )

² ( P i k i )

e ₁

—

( P i — k + m )

² ( P i ^k 2 )

n q ²

e ₂

- U i =

u2 x

*

{ ( P i ^k 2 ) e 2 ( p i ⁺ k i ^{+ m} ) e i

—

—

( P i k i ) e i ( p i

—

^^

k 2 + m

) e 2 } ^u i =

= i

n q ²

* u ₂ Mu ₁,

где обозначено

M = ( P i k 2 ) e 2 ( P i + k i + m ) e i — — ( P i k i ) e i ( P i — k 2 + m ) e 2 .

Найдем квадрат модуля матричного элемента H вз| .

Фотон при взаимодействии с частицей поворачивает плоскость своей поляризации. Но частица до взаимодействия может находиться в различных состояниях с амплитудой u , в том числе, согласно Дираку, в состоянии с отрицательной энергией [4]. Для того чтобы исключить состояния с отрицательной энергией, вводится т. н. проекционный оператор R [4], или матрица плотности [8]. Проекционный оператор для ча-

стицы вводится по принципу

R = E + E

2 E

i,   E > 0

0,   E < 0

где Е – энергия частицы. Переходя к операторам, найдем [9]:

12 mu ,   E > 0

up + m =            [3].

[ 0, E < 0

Используя проекционный оператор (18), мы мо-

жем при суммировании по состояниям частицы не обращать внимания на знак ее энергии.

Таким образом:

I H 4

24 n q

( P i k i ) 2 ( P i ^k 2 ) 2 k i ^k 2

E ( u * MU i ) 2 =

E

n² q ⁴          _x

( P i k i ) 2 ( P i ^k 2 ) 2 ^k i ^k 2

E ( U * R 2 Mu i )( U * R i M ⁺ U 2 ) =

E

-----q ⁴ m ₂ ----E ( U * R 2 MR i M ⁺ U 2 ) .

( P i k i ) ( P i ^k 2 ) ^k i ^k 2 E                      ⁷

Использовано условие нормировки амплитуд волновых функций частицы в виде uu * = 2 m [3], M ⁺ — эрмитово сопряженный оператор [4].

*

u Lu =Sp L

[5], а также проекционный оператор (18), най-

дем:

I H вз^ =

2n² q ⁴ m

,    _ .2 ,    _ .2 . . ^x

( P i k i ) ( P i k 2 ) ^k i k 2

x E ( u * R ₂ MR _i M ⁺ u ₂ ) =

E

_       n q m

2 ( P i k i ) ² ( P i k 2 ) ² E i E 2 k i k 2

Sp A ,

где A = ( -p 2 + m ) M ( -p i + m ) M ⁺ , E i и E 2

– энергии

частицы до и после взаимодействия с фотоном.

Прежде чем находить Sp A , сделаем существенное упрощение задачи. Предположим, что

первоначально рассеивающая частица находится в состоянии покоя, т. е. p i = 0. Фактически мы выбираем систему отсчета, связанную с частицей до ее взаимодействия с квантом. В этом случае ( P i k ) = p 0 k ⁰ — p i k = E i k = mk , где p ⁰ = E i = m . В рациональной системе единиц энергия неподвижной частицы равна ее массе. Следовательно, ( P i k i ) = mk i и ( p i k 2 ) = mk 2 .

Матрица (17) преобразуется к виду

M = m |^ k 2 e 2 ( j^ i + k c i + m ) e i

—

^— k i ^e i ( ^p i

^^

— k2

+ m ) e 2 ].

Формула (20) приобретает вид

I H вз2

---з q з Sp A .

2 m ³ k ₁ ³ k ₂ ³ E ₂

h вз = , ₃, l _F sp a = 2 m ³ k ₁ ³ k ₂ ³ E ₂

В (22) использовано E i = m . Обозначение М сохраняем для величины

16 з² q ⁴ mk ₁ k ₂ E ₂

( ^e i e 2 ) 2

1^{6 з} 2 ( Й с ) 4 q ⁴    ₂

—-—-— ---cos 0.

c E ₁ E ₂ k ₁ k ₂

M = k 2 e 2 (: P i + k i + m ) e i — k i e 1 ( i ^ i — k 2 + m ) e 2 ,

—

что не должно вызвать недоразумений.

Нахождение шпура Sp A довольно громоздко, но носит технический характер. При вычисле-

ниях нужно помнить, что шпур от произведения нечетного числа операторов равен нулю, а от произведения четного числа операторов его можно вычислить по формуле

В (28) использовано ( e i e 2 ) = cos 0, где 0 — угол поворота плоскости поляризации переизлучен-ного фотона относительно плоскости поляризации фотона, падающего на частицу (рис. 1). Кроме того, осуществлен обратный переход от рациональной к абсолютной системе единиц измерения СГС.

3. Интенсивность света после взаимодействия с веществом

Sp ft A j = £ ( —i ) n ( A i A n ) x j = i        n = 2

x

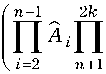
Подставляя (28) в (7), найдем дифференциальное эффективное сечение взаимодействия «фотон–частица»:

A

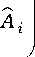
d G = 23 H вз^ Й

k ₂    d k 2

( 2з Й ) ³ c ^д E F

d Q

Результат вычислений Sp A можно найти в [9]:

Sp A = 32 m ² k 2 k 2 ( e i e 2 ) ² +

+ 8 mk^ ( kk ) ( k i — k 2 ) =                 (25)

= 8 m ² k 2’ k 2 ² [4 ( ee ) ² + ⁽ kk ^{)( k i —} k ²) .

mkk

= ^{4 q k 2} cos² 0 ^d 2 d q . E 1 E ₂ k 1       d E _F

Возвращаясь к 3-векторам и их модулям, найдем производную d k 2 / d E _F при отсутствии углового рассеяния фотона. Энергия системы «фотон–частица» в конечном состоянии равна:

Найдем в (25) отношение

(kik2) = (k0k0 — kik2) = k1k2          k1k2

( k 0 k 0 — k i k 2 cos a )

k ₁ k ₂

k ⁰ k ⁰

= ^{1 2} — cos a = i — cos a, k ₁ k ₂

где a — угол между начальным и переизлучен-ным фотоном.

Явление взаимодействия «фотон–частица» в законе Малюса не связано с отклонением пере-излученного фотона от первоначального направления, поэтому угол a = 0. Следовательно, отношение

⁽ k i k 2 ) = ₀

k ₁ k ₂

и формула (25) приобретают вид

Sp A = 32 m ² k i k 2 ( e _i e ₂ ) ² .                        (27)

Подставляя (27) в (22), найдем:

22   24

E f = ck 2 + E 2 = ck 2 + \ P 2 c + m c =

= ^ck 2 ⁺ V⁽ k i ^{— k} 2 ^{) 2 c 2 + E} 1 .

Использован закон сохранения 3-импульса в виде P2 = ki — k2. Все импульсы направлены по одной прямой (рис. 1), поэтому в законе сохранения используем алгебраические значения 3-им- пульсов.

Производная выражения (30) равна dEd

F = c + d k2d c2

^— — ⁽ k i ^— k 2 ) =

E ₂

E2 — cp2 _ Ei c . E2   J

Использован закон сохранения энергии в виде ^E 2 ^{— E} i = ^c ( ^k i ^{— k}2 ) = ^cp 2 .

Подставляя с d k 2 / d E _F = E 2 / E i в (29), найдем:

dg = ^q ^ cos2 0dQ .(32)

E 1 ² k 1

Отметим, что величина сdk2 / dEf зависит от вида процесса взаимодействия «фотон–частица». Например, найдем производную dk2 / дEf при возможности углового рассеивания фотона. Такая ситуация имеет место при анализе эффекта Комптона. Энергия системы «фотон–частица»

в конечном состоянии в этом случае равна:

E f = ck 2 + E 2 = ck + p p c c ² + m ² c ⁴ =

= ^ck 2 ⁺ ^( ^k 1 - ^k 2 ) ^c 2 ⁺ E 1 =                  ⁽³³⁾

= ck 2 + k 2 c ² - 2 kkc ² cos a + k 2 c ² + E 2 .

Производная этого выражения:

d E     5 E

—F = c + —² = c -

9 ^k2

^{d k}2

c ²

— ( k cos a - k ₂) =

E 2

E 2 k₂ - c ( kk cos a -

k ²) -

= c

= c

E ₂ k ₂

E 2 ^k 2 ^{- c}

( ^- mc ⁽ k i ^- k ) + k i k 2 ^{- k} 2 )

E ₂ k ₂

ck ₁ E ₁

. E ₂ k ₂

При выводе использована формула эффекта Комптона k 1 k 2 ( 1 - cos a ) = mc ( k i - k ) [11], E i = mc ² и закон сохранения энергии E 1 + kc = = ^E 2 ⁺ k 2 ^c .

Перейдем в (32) от дифференциального эффективного сечения взаимодействия «фотон– частица» к интенсивностям излучения до и после взаимодействия.

По определению дифференциальное эффек- тивное сечение процесса рассеяния волны в классической электродинамике dСкл = dP / 10 [12], где dP – поток энергии рассеянного в телесный угол dQ излучения; 10 — интенсивность падающего излучения.

Свяжем данное определение дифференциального эффективного сечения взаимодействия с его квантовым аналогом (6). Учитывая dNрас

dP

=      и j 0

Й © 2

I ₀

Й Ю 1

найдем

Следовательно, учитывая (32), найдем:

dскл = ~ d° = ^q, ^2 cos2 0dQ .(35)

^кл    k 1         E 1 ² k 1 ²

Интенсивность излучения после взаимодей- ствия dP _ 10d°кл dS   R2 dQ , где R – произвольный радиус сферы, описанной вокруг частицы. Не уменьшая общности вывода, примем (по аналогии с классическим радиусом электрона) R = 2q2 / E1. В результате получаем закон Малюса в виде

I = 1 0 k 2-cos² 0 = 1 0 ^2-cos² 0 . (36) k 1 © 1

При © 1 = © 2 формула (36) переходит в классический закон Малюса (1). Этим объясняется выбор R = 2 q ² / E 1 .

Заметим, что формулу (36) нельзя получить ни при каких условиях из формулы Клейна – Нишины [9] для эффекта Комптона. Формула (36) относится к переизлучению фотонов строго вперед после взаимодействия с частицей. В эффекте Комптона при переизлучении фотона вперед изменения его частоты не происходит.

Согласно формуле (35) переизлучение фотона вперед с поворотом его плоскости поляризации происходит только при взаимодействии с заряженной частицей. Однако установлено, что поворачивают плоскость поляризации света либо асимметричные, в том числе нейтральные, молекулы, либо асимметричные кристаллы, обладающие асимметрией поля сил, связывающих частицы в кристаллической решетке [13]. Поэтому под величиной q нужно понимать не полный заряд частицы, а ту часть заряда, которая определяет асимметричную часть электрического поля вокруг молекулы, создающего силы взаимодействия Ван-дер-Ваальса, либо вокруг частицы в кристаллической решетке. В целом же частица может быть электрически нейтральной. Если электронейтральная частица создает вокруг себя полностью симметричное электрическое поле (при q = 0, величина dС_кл = 0), интенсивность I ~ dС_кл / q ⁴ становится неопределенной. С этой точки зрения формула (36) имеет более общий характер, чем (35).

Полученная формула (36) показывает, что при переизлучении на частице частоты излученного и поглощенного света могут не совпадать. Частица может переизлучать в стоксовском © 2 < © 1 или антистоксовском © 2 > © 1 режимах.

В используемой теории возмущений разложение волновой функции в ряд по собственным функциям невозмущенного гамильтониана осуществляется вблизи резонансной энергии до членов первого порядка малости. Поэтому интенсивность переизлучения оказалась пропорциональной ©2 [12]. Вдали от резонанса необхо- димо вводить поправку, связанную с шириной энергетических уровней электронов у в переиз-лучающей частице [4; 5; 8]. Отметим также, что учет ширины энергетического уровня не меняет поляризационных свойств излучения [8].

При низких частотах можно использовать поправку к формуле (36) для классической дипольной переизлучающей частицы [12] в виде

2    2 ²     22

(®0 - ®i ) + ®i У где i = 1, 2 , too — резонансная частота переизлу-чающей частицы. Этот вид поправки следует из электромагнитной теории света. В этом формула (36) принимает вид случае

I = 1 0

to 4 ( ^to 0 ^{- to} 2 )

^{to 1} ( ^to 0 - ^to 2 ) +

2 2

⁺ ^У ₂ cos² 0 .

2 2 to 2 Y

Вблизи резонанса, дим к формуле (36).

учитывая to i «to o , При относительно

прихо-малых

частотах to i << to o из (37) находим: 4

I = I o -2- cos² 0 .

to14

При очень больших частотах to i >> to o получаем классическую формулу (1) или, точнее, формулу с сохраненной частотой переизлучения to i = to 2 . Во всех случаях предполагается to i « to 2 и to i >> у.

При высоких частотах (следовательно, в квантовой области) формула (36) должна быть преобразована с использованием квантовой поправки [14] в виде сомножителя:

[Y)                1              .

12 J /           a2 Y ² '

• (too - toi ) + 4

• ^{2 (to} o ^{- to} i ) ²

I = 1 o 2------------ ^to                2

• 1    (to0 -to2 )

  +l!

  —4- cos² 0 .

  +

  
  
  
  

Отметим, что вблизи резонанса при to i « to o обе поправки (классическая и квантовая) идентичны:

.        2 ) ² _{+ Ш} 2 Y²

(too -toi) (too +toi ) + to2 y2

( ^to o ^-to i ) ^{4 to 2 + to 2 y 2}

III _____________1_____________.

12^J /           a2   Y²

(too - toi ) +

Вблизи резонанса аналогично формуле (37) формула (38) переходит в формулу (36). Так же как и формула (37), при высоких частотах формула (38) переходит в классическую формулу (1). При низких частотах в области классической электродинамики нужно пользоваться формулой (37).

В заключение оценим численное значение частотного коэффициента в формуле (36). В [15] приведены спектры поглощения и излучения кристалла CaSiO 3 ■ Pb и спектр излучения кристалла CaWO 4 ■ Pb, облученного линией Х 1 = 2537 ^A. Для CaSiO 3 ■ Pb используем спектральную линию максимальной интенсивности поглощения Х 1 = 2527 A. Спектральные линии максимальной интенсивности излучения равны: для CaSiO 3 ■ Pb — ^ 2 = 2534 jA , для CaWO 4 ■ Pb — ^ 2 = 2544 A. Следовательно, для CaSiO 3 ■ Pb коэффициент to² / to² =X² / X² = o, 994 и для CaWO 4 ■ Pb — to² / to² = o, 995. При практическом использовании закона Малюса в виде (1) мы делаем ошибку, не превышающую для данных кристаллов 0,5 %.

Заключение

Используя метод расчета на основе диаграммной техники Фейнмана, можно найти форму закона Малюса, учитывающую квантовый характер излучения. Эта форма закона Малюса не связана с формулой Клейна – Нишины для эффекта Комптона и не может быть получена из этой формулы.

Квантово-механическая форма закона Малю-са, в отличие от классической, позволяет учесть ту часть импульса при взаимодействии «фотон– частица», которая передается частице. За счет этого направленное вперед излучение после взаимодействия имеет меньшую интенсивность, чем рассчитанное на основе классического закона Малюса.

В квантовом объяснении закона Малюса важное значение имеет несимметричность электрического поля, создаваемого молекулами в веществе или частицами в узлах кристаллической решетки. Несимметричность электрического поля связана с геометрической несимметричностью структур, создающих поле.

Проведен анализ связи закона Малюса с конечной шириной энергетических уровней пере-излучающих частиц.