Закономерности кластеризации динамики численности популяций, находящихся в процессе расселения особей по линейному ареалу
Автор: Кулаков М.П.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Региональный прогноз. Математическое моделирование
Статья в выпуске: 4 т.18, 2015 года.
Бесплатный доступ
Работа посвящена исследованию механизмов формирования сложной динамики и кластеризации в линейных цепочках популяций, локально связанных между собой миграцией. Подробно моделируется процесс расселения особей в такой цепочке из некоторой единственной изначально не пустой субпопуляции. Показано, что помимо начальной численности формируемый тип динамики и вид пространственного распределения сложным образом зависит от длины цепочки популяций.
Ареал, метапопуляция, миграция, система связанных отображений, синхронизация, кластеризация
Короткий адрес: https://sciup.org/14328929
IDR: 14328929 | УДК: 517.9:574.34
Текст научной статьи Закономерности кластеризации динамики численности популяций, находящихся в процессе расселения особей по линейному ареалу
Одним из проявлений пространственного расселения реальных биологических популяций является пятнистое или мозаичное их распределение, представляющее собой систему разбросанных по ареалу скоплений особей, локальных популяций или субпопуляций [1, 8]. Кроме того, особи активно мигрирующих видов способны несколько раз за сезон покинуть один очаг и переселиться в другой. В результате каждая из субпопуляций, состоящая из особей со схожими характеристиками, оказывается связана с такими же субпопуляциями миграционными связями, образуя метапопуляции [12]. Направления перемещений и форма самого ареала для таких популяций оказываются тесно связанными с особенностями ландшафта и структурой биотопов. При их относительном постоянстве можно говорить о том, что пространственно распределенные популяции формируют цепочки из локальных популяций (линейные или пространственные) с глобальными или не глобальными связями, определяемыми дальностью и интенсивностью миграционных потоков [7, 10, 11, 14, 16].
В данной работе исследуются механизмы и закономерности формирования пространственной динамики в популяциях, представляющих собой линейные цепочки из групп особей или субпопуляций, локально связанных между собой миграцией. Изучается процесс расселения особей по линейному ареалу из единственного локально- го участка с ненулевой численностью. Подобная форма ареала возникает для популяций животных, у которых ареал вытянут вдоль какого-либо природного объекта, например русла реки, долинного комплекса, склона горы, границы между лесом и лугом [1]. Заселение ареала из единственной локальной популяции наблюдается, к примеру, в случае катастрофического уничтожения популяции почти на всем ареале и последующего его восстановления из единственной выжившей популяции. Кроме того, такая ситуация характерна для новых и пионерских для данной территории видов, заселяющих территорию, например в ходе сукцессии [1, 8].
В качестве модели динамики такой популяции используется цепочка локально диссипативно связанных логистических отображений Рикера [3–6, 10, 17, 18]. Одним из интереснейших феноменов, который возникает в таких моделях, является кластеризация, т.е. образование групп синхронных элементов [2, 4, 13]. Данное явление, применительно к рассматриваемой задаче, заключается в том, что абсолютно идентичные смежные популяции образуют группы или кластеры, внутри которых наблюдается когерентная или синхронная динамика [4, 5]. Достаточно давно известно, что формирование такой динамики сложным образом зависит от начальных численностей, а при различных начальных численностях таких кластеров может быть несколько, они могут иметь разный размер и принципиально разные динамические характеристики [2, 4, 5]. Кроме того, цепочки связанных колебательных элементов демонстрируют интересное явление, названное химерным состоянием (chimera states). Это особое динамическое состояние, когда внутри кластера отдельные элементы выбиваются из единой синхронной динамики, по сути демонстрируя нерегулярное поведение [9, 15]. Вместе с тем вопрос формирования кластеров в цепочках локальных популяций разных длин из единственной ненулевой популяции остается открытым.
Система связанных отображений
В поставленной задаче все локальные популяции выстроены в линейную цепочку, в которой связаны лишь смежные субпопуляции (локальная связь). Логично пронумеровать их от 1 до N , где N – число локальных популяций или длина цепочки. В результате некоторая i -я популяция связана лишь с двумя своими ближайшими соседями, т.е. с i -1 и i +1, а первая лишь со второй, а N -я лишь с N -1-й. В этом случае границы оказываются незамкнуты (рис. 1 а ), но как будет показано ниже, этот случай принципиально не отличается от случая замкну-
Рис. 1. Цепочка связанных популяций с линейным ареалом (а) без замыкания и (б) с замыканием границ (кольцо из популяций). Стрелки – перемещения особей в местах контакта субареалов
Pic. 1. The chain of connected populations in a linear areal with unclosed (a) and (b) closed borders (the populations’ circle). The arrows show the migration of individuals between adjacent sub-areal territories тых границ, когда 1-я популяция связана еще и с N-й, а популяция образует кольцо из субпопуляций (рис. 1б). Тогда если xn(i) – численность локальной популяции с номером i (i = 1,2,..., N) в n-й дискретный момент времени, то динамику всей цепочки можно описать системой вида:
(1) (1) (2)
x n + 1 (1 m ) f ( x n ) + fm ( x n )
<Y( i ) = f1-2wVfY( i fY( i "^ч-А fY( i +1)V x n + 1 (1 2 m ) f ( x n ) + m ( x n ) + m ( x n )
( N ) Y( N fY( N " 1)1 ^ x n + 1 (1 m ) f ( x n ) + m ( x n )
где m –коэффициент миграции. Множители 1 – m и 1 –2 m указывают на долю местных особей, оставшихся на данной территории после миграции. Функция f(x)=ax exp (–x) – функция локального воспроизводства, выбранная в виде запас-попол-нения Рикера, которая задает локальную динамику в отсутствии миграционной связи, т.е. если m=0 , то:
x ni + 1 = f ( x n ) = a x ni e xp ( - x ni ) ) , (2) где a – репродуктивный потенциал или скорость роста i -й субпопуляции. Система (1) имеет естественные ограничения - 0 0 , которые при неотрицательных начальных численностях x 0 1 ) > 0 гарантируют ограниченность всех ее траекторий.
Модель вида (1) принято называть системой связанных отображений с локальной связью [2]. Для таких систем хорошо известны и подробно исследованы качественные механизмы потери устойчивости и формирования периодической динамики в системе подобного рода [3, 10, 17]. В частности, в случае полной идентичности всех локальных субпопуляций и симметричной миграции, нетривиальная неподвижная точка системы (1) совпадает с аналогичной точкой уравнений (2) и равна x (1) = x (2) = _ x ( N ) = x = ln ( a ) . Первая бифуркация в системе (1) – удвоение периода и появление синхронного цикла длины 2 у всех локальных популяций, т.е. такого, что x® = x n2^ = „. = x n^ N ) ^ x при n ^* . С ростом репродуктивного потенциала a эволюция синхронных динамических режимов идет по сценарию Фейгенбаума. Последующие бифуркации неподвижной точки соответствуют рождениям вокруг неустойчивой неподвижной точки различных несинфазных циклов периода 2 в отдельных частях цепочки. Это проявляется в том, что при определенных начальных значениях численностей среди N переменных системы (1) появляется одна переменная, которая оказывается несинхронной всем остальным N -1 переменным.
Например, это режимы вида: xn" * x^ = * = xnN), х(2) * -< = х(3) = = ■>N) и т.д. при n ^ да. Число ва-n “ “ n риантов таких несинхронных режимов будет равно N. Снижение параметра миграции m приводит к тому, что несинхронных режимов может быть уже 2, а общее число несинхронных режимов равно числу сочетаний из N по 2. Дальнейшее уменьшение параметра m приводит к тому, что число видов несинхронных циклов будет огромным.
Однако эти рассуждения полностью верны лишь для периода колебаний равного 2, когда колебания в разных частях цепочки могут быть лишь синхронными и несинхронными. С ростом периода колебаний несинхронный режим может быть реализован большим числом способов, которые отличаются фазой колебаний. Поэтому число возможных в системе (1) динамических режимов также зависит от периода колебаний. В любом случае, все эти режимы наряду с полностью синхронным циклом сосуществуют и реализуются в зависимости от начальных численностей. В результате возможные динамические режимы системы (1) представлены сложной иерархией мульти-стабильных режимов.
Частным случаем мультистабильности является явление кластеризации, которое в биологической трактовке заключается в том, что рядом стоящие синхронные между собой популяции можно объединять в группу и рассматривать как отдельную популяцию, ведущую себя как локальная популяция. Как было показано в [5], это позволяет значительно упростить исследование модельных уравнений и явно описывать различия в скоростях роста локальных популяций, варьируя размер кластеров.
С другой стороны, каждый из несинхронных режимов и видов кластеров имеет свою область притяжения, т.е. такую область фазового пространства, начальные значения из которой приводят только к этому режиму. В [4] предложена методика определения и исследования таких областей. Было показано, что изменение популяционных и миграционных параметров приводит к значительным их трансформациям, которые сопровождаются изменениями размеров и размерностей областей притяжения.
Вместе с тем остается открытым вопрос о закономерностях возникновения кластеров в системах миграционно связанных популяций в зависимости от размеров и формы ареала. В частности, от длин цепочек популяций, описываемых системой (1). Интересным также является изучение процесса расселения особей из единственной локальной популяции вдоль линейного ареала и возникающих динамических режимов.
Рассмотрим динамические режимы, которые возникают в системе (1), соответствующие случаю, когда начальная точка зафиксирована из некоторой части бассейна притяжения при вариации параметров и размеров цепочки.
Формирование кластеров в цепочках популяций
На рис. 2 а продемонстрирован процесс образования двух кластеров в цепочки из 100 ми-грационно связанных популяций, описываемых системой (1) при N= 100. В центре рис. 2 а , а также в левых частях рис. 2 б и в , в плоскости номера субпопуляции i и номера сезона n показана динамика системы (1). Черные области соответствуют минимальным значениям фазовых переменных, а белые – максимальным, серым выделены значения между ними.
Несложно заметить, что количество итераций, которое требуется системе (1), чтобы выйти на устойчивый кластер, прямо зависит от количества связанных элементов. Так на рис. 2 а показано, что в цепочке из 100 связанных популяций из единственной субпопуляции с ненулевой начальной численностью ( x 01) = 4 , x 0 i ) = 0 , i=2,3,...,N) , с одной стороны, требуется 99 сезонов на заполнение всего ареала, а с другой – что примерно через 210 итераций все 100 элементов образуют два устойчивых неравных кластера.
Достаточно предсказуемо, что в цепочках связанных популяций, в которых связанными оказываются первая и последняя субпопуляции, а ареал представляет собой кольцо (рис. 1 б ), формирование кластеров происходит быстрее (рис. 2 б и в ). Система уравнений, описывающая динамику, в этом случае имеет вид:
(1) (1) ( N ) (2)
x n + 1 = (1 2 m ) f ( x n ) + m ( x n ) + m ( x n )
"' .
( i ) -П-2т1<Гг( i fr( i -1Ь fr( i +1)1
x n + 1 = (1 2 m ) f ( x n ) + m ( x n ) + m ( x n ) , (3)
( N)-(]-2m}f(x(N fjc( N -1)) fjc(1)')
I x n + 1 = (1 2 m ) f ( x n ) + fm ( x n ) + fm ( x n )
в которой, в отличие от системы (1), первое уравнение связано с последним. Поэтому из единственной субпопуляции ( x 01) = 4 ) расселение одновременно идет в две стороны и на полное заполнение всего ареала требуется всего 48 сезонов, а не 99, как для системы (1), и формирование полностью устойчивых кластеров наступает уже через 110 итераций. Для большей информативности на рис. 2 а-б приведены графики, соответствующие
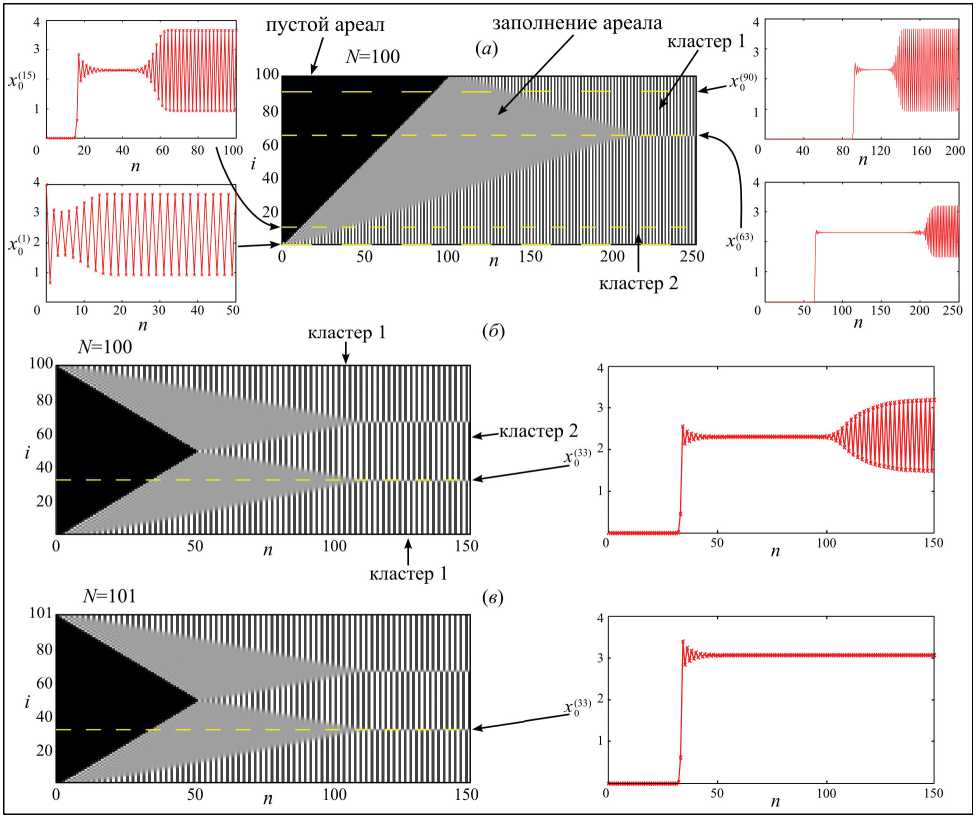
Рис. 2. Формирование двух кластеров в (а) цепочке, (б) кольце из 100 связанных популяции и (в) кольце из 101 популяции, из единственного ненулевого местообитания, при a=10, m=0,1, x 0 (1) = 4 , и x 0 ( i ) = 0 (i=2,3,...,N )
Pic. 2. The formation of two clusters with (a) the linear chain, (b) the circle of 100 related populations, and (c) the circle of 101 populations formed of a single non-empty habitat, at a=10, m=0,1, x 0 (1) = 4 and x 0 ( i ) = 0 (i=2,3,...,N )
временным реализациям системы (1) и (3) для некоторых субпопуляций в рассматриваемой цепочке или кольце из связанных популяций.
Приведенные примеры, с одной стороны, демонстрируют механизм образования кластеров в системах связанных отображений, а с другой показывают, каким образом может проходить расселение особей по однородному линейному ареалу и какие режимы при этом возникают. Черным треугольникам на рис. 3 соответствует период, когда изначально пустые местообитания постепенно заполняются. Сплошным пятнам серого цвета треугольной формы соответствует длительный период релаксации динамики популяций, который выражается в быстро затухающих колебаниях (см гра- фики на рис. 2). Далее они быстро сменяются колебаниями численности периода 2, и во всех трех случаях формируется два кластера, которые показаны чередующимися полосами белого (максимум) и темно-серого цвета (минимум численности).
В двух последних примерах (рис. 2б и в) первый и последний элементы системы (3) связаны между собой, и динамика между ними полностью синхронная. Поэтому наблюдаемые на рис. 3б и в три полосы соответствуют двум кластерам. В третьем случае (рис. 2в), когда кольцо состоит из 101 субпопуляции, между кластерами выделяется две четкие границы, элементы (субпопуляции) которых после периода релаксации, за счет соседних очагов с противофазной динамикой, не испытывают колебаний (граничный эффект). Эти границы на рис. 2в показаны тонкими серыми полосами, исходящими от вершин серых треугольников. Вместе с тем в кольце из 100 связанных субпопуляций такой границы нет. В подтверждении этого на рис. 3б и в приведены графики 33-го элемента ( xn(3 ) ), который не осциллирует в кольце из 100 связанных элементов и осциллирует в кольце из 101 элемента. Это означает, что число элементов в системе связанных элементов влияет на характер динамики и формируемые кластеры.
Интересно отметить, что, например, при рассматриваемых начальных условиях и значениях параметров в кольце из 102 и 103 элементов, описываемых системой (3), формируется лишь полностью синхронная динамика между всеми элементами. В кольце же из 104 элементов вновь появляются два кластера. Кроме того, обнаружено, что в цепочке, описываемой системой (1), из 101, 103 элементов образуется три кластера, а из 104 – четыре.
При значительном уменьшении коэффициента миграций из единственной субпопуляции с ненулевой численностью способна сформироваться фаза кластеризации, похожая на турбулентную (рис. 3а). В этом случае размер каждого кластера (группа рядом стоящих элементов) варьируется от 2 до 3. Следует отметить, что формирование такой фазы кластеризации и полное заполнение всех местообитаний происходит через 158 сезонов, а не через 99, как в прошлом случае (рис. 2а); а при замыкании границ линейного ареала в кольцо число возможных кластеров меняется незначительно (42 в линейной цепочке и 40 у кольца). В кольце, так же как и в прошлом случае, полное заполнение ареала происходит быстрее (рис. 3б). Кроме того, время для заполнения всех местообитаний значительно увеличивается с уменьшением силы связи (рис. 3в и г).
Также оказалось, что при столь малых значениях коэффициента миграции начальное распределение слабо влияет на формируемую картину пространственного распределения – создаются режимы близкие к турбулентной фазе с малыми относительными числами заполнения кластеров, или полностью когерентная фаза. Это выражает-
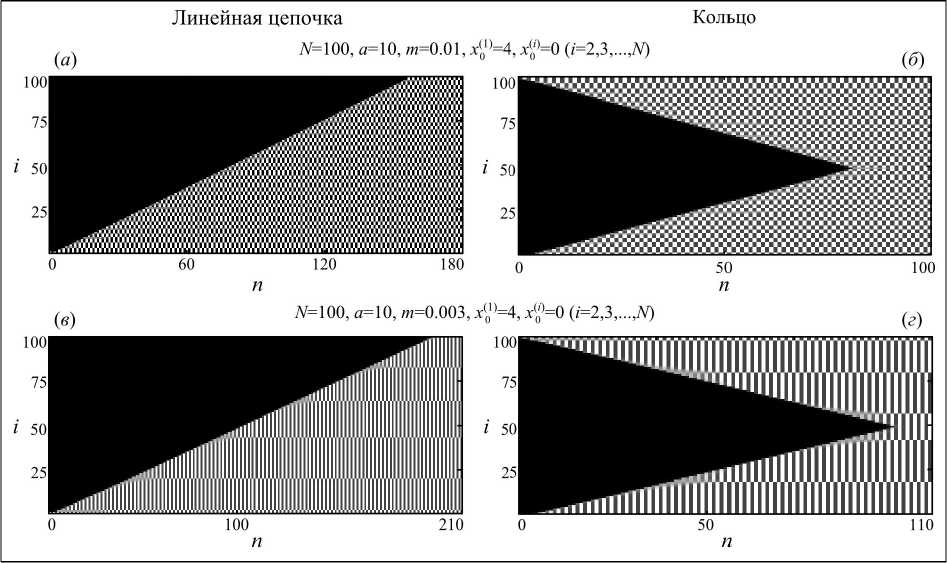
Рис. 3. Динамика системы (1), которая демонстрирует образование (а) 42 и (в) 6 кластеров в цепочке из 100 субпопуляций при разной силе связи; динамика системы (3), которая демонстрирует образование (б) 40 и (г) 6 кластеров из 100 субпопуляций в кольце 100 субпопуляций
Pic. 3. Dynamics of the system (1) demonstrating the formation of (a) 42 and (b) 6 clusters i n the linear chain of 100 subpopulations at different relation strength; dynamics of the system (3) demonstrating the formation of (c) 40 and (d) 6 clusters in the circle of 100 related subpopulations
ся в том, что по мере того как собственные числа системы (1) или (3) один за другим выходят из единичного круга, размерность устойчивого многообразия, в котором реализуются синхронные режимы, падает. В результате при очень малых m когерентная фаза оказывается устойчивой только на диагонали первого октанта, т.е. на луче х(1)=х ( 2)=...х№>0 , а любые вариации начальной точки относительно нее приводят лишь к режимам, близким к турбулентной фазе. Однако экспериментально установлено, что существуют достаточно узкие диапазоны параметра миграции, при которых размеры кластеров оказываются достаточно большими. Например, при m=0,003 в системе (1) и (3) из единственного ненулевого элемента ( x 00) ) формируются 6 кластеров, размер которых варьируется от 2 до 23 элементов (рис. 3 в и г ).
Выводы
В работе показано, что расселение особей в линейной цепочке или кольце из единственной субпопуляции с ненулевой численностью проходит в два этапа. На первом этапе происходит первичное заполнение ареала, которое сопровождается быстрым ростом численности, серией релаксационных колебаний и формированием квазиста-ционарной динамики, когда субпопуляции продолжительное время практически не испытывают колебания. По всей видимости, это связано с тем, что продолжающаяся миграция на пустые территории компенсирует колебания численности, т.е. не успевают «включиться» плотностно-зависимые механизмы, вызывающие колебания. На втором этапе квазистационарная динамика разрушается и формируются устойчивые колебания численности. Неожиданно оказалось, что время, которое требуется каждой субпопуляции для формирования устойчивой периодической динамики, нелинейно зависит от ее расположения в цепочке или кольце. Численно легко выделяется «граничная» субпопуляция (или субпопуляции для кольца), до которой формирование колебания численности в локальных популяциях происходит тем раньше, чем ближе они к началу цепочки (субпопуляции с начальной ненулевой численностью). Напротив, после такой граничной субпопуляции формирование колебаний происходит раньше у самых последних элементов в цепочке. При определенных длинах цепочки или кольца эти колебания в разных частях ареала становятся несинхронными и формируются кластеры. Кроме того, в простейшем случае граничная субпопуляция разделяет эти кластеры, и в ряде случаев она сама не испытывает колебаний. Последнее определяется чет- ным или нечетным порядком числа субпопуляций в цепочке или кольце.
Было выявлено, что при очень незначительной миграции полностью отсутствует второй этап расселения. После начального заполнения ареала, который занимает намного больше времени, сразу формируется периодическая динамика, которая при различных длинах цепочек приводит к кластерам разнообразных размеров. Таким образом, в работе была показано принципиальное наличие сложной зависимости вида и размеров формируемых кластеров от длины цепочки миграционно связанных популяций.
Список литературы Закономерности кластеризации динамики численности популяций, находящихся в процессе расселения особей по линейному ареалу
- Дажо Р. Основы экологии/пер. с франц. М.: Прогресс, 1975. 415 с
- Кузнецов С.П. Универсальность и подобие связанных систем Фейгенбаума//Изв. вузов: Радиофизика. 1985. Т. 27, № 8. С. 991-1007
- Кулаков М.П., Аксенович Т.И., Фрисман Е.Я. Подходы к описанию пространственной динамики миграционно-связанных популяций: анализ синхронизации циклов//Региональные проблемы. 2013. Т. 16, № 1. С. 5-15
- Кулаков М.П., Фрисман Е.Я. Бассейны притяжения кластеров в системах связанных отображений//Нелинейная динамика. 2015. Т. 11, № 1. С. 51-76
- Кулаков М.П., Фрисман Е.Я. Использование эффекта кластеризации в системах связанных отображений для описания динамики метапопуляций//Математическая биология и биоинформатика. 2015. Т. 10, № 1. С. 220-233
- Кулаков М.П., Фрисман Е.Я. Синхронизация 2-циклов в системе симметрично связанных популяций, запас-пополнение в которых описывается функцией Рикера//Известия вузов. Прикладная нелинейная динамика. 2010. Т. 18, № 6. С. 25-41
- Логофет Д.О. Способна ли миграция стабилизировать экосистему? (Математический аспект)//Журнал общей биологии. 1978. Т. 39. С. 123-129
- Примак Р. Основы сохранения биоразнообразия/пер. с англ. О.С. Якименко, О.А. Зиновьевой. М.: Изд-во научного и учебно-методического центра, 2002. 256 с
- Abrams D. M., Strogatz S.H. Chimera states for coupled oscillators//Physical review letters. 2003. Vol. 93, N 17. P. 1-4
- Gyllenberg M., Söderbacka G., Ericson S. Does migration stabilize local population dynamics? Analysis of a discrete matapopulation model//Math. Biosciences. 1993. Vol. 118. P. 25-49
- Hanski I. Gyllenberg, M. Two general metapopulation models and the core-satellite species hypothesis//American Naturalist. 1993. Vol. 142, N 1. P. 17-41
- Hanski I. Metapopulation Ecology. Oxford University Press, 1999. 328 p
- Kaneko K. Clustering, coding, switching, hierarchical, ordering, and control in network of chaotic elements//Physica D. 1990. Vol. 41. P. 137-172
- Kaneko K. Relevance of dynamic clustering to biological network//Phisica D. 1994. Vol. 75. P. 55-73
- Kuramoto Y., Battogtokh D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators//Nonlinear Phenomena in Complex Systems. 2002. Vol. 5, N 4. P. 380-385
- Opdam P. Metapopulation theory and habitat fragmentation: a review of holarctic breeding bird studies//Landscape Ecology. 1991. Vol. 5, N 2. P. 93-106
- Udwadia F.E., Raju N., Dynamics of Coupled Nonlinear Maps and Its Application to Ecological Modeling//Applied mathematic and computation. 1997. Vol. 82. P. 137-179
- Vanderlei Manica, Jacques A.L. Silva. Population distribution and synchronized dynamics in a metapopulation model in two geographic scales//Mathematical Biosciences. 2014. Vol. 250. P. 1-9


