Закономерности, присущие потокам высокоэнергичных частиц солнца: экспериментальные данные и вероятностная модель

Появление в окрестностях Земли высокоэнергич ных частиц солнечного происхождения – солнечных космических лучей ( СКЛ ) – является для нас вероят ностным явлением , которое , однако , подчиняется вполне конкретным закономерностям . Понять эти за кономерности позволяет анализ экспериментальных данных . При этом важно учесть два обстоятельства . Во - первых , что экспериментальным данным присущи не только статистические , но и систематические ошибки [1]. Во - вторых , что анализ является только тогда эффективным , когда он базируется на коррект ной методологии исследования [2, 3, 4], соответст вующей характеру исследуемого явления .

Нарушение этих основополагающих принципов исследования привело к тому , что имеет место це лый ряд ничем не обоснованных мифов [5–8], свя занных с появлением событий СКЛ .

Например , мифы о том , что большие события СКЛ появляются чаще всего до и после активной фазы солнечного цикла [5, 6] и что есть тенденция большим событиям СКЛ появляться через 2–4 г . после максимума солнечной активности ( СА ) [7].

Во многих работах по анализу частоты появления событий СКЛ пользовались годичными интервалами , отчитываемые или от максимума [7], или от минимума [8] цикла СА . Такой метод представляется ошибоч ным , так как в одни и те же выбранные интервалы времени в разные солнечные циклы попадают годы с совершенно разным уровнем СА . Вследствие этого при выбранной методике поиск какой - либо однознач ной зависимости частоты появления событий СКЛ от уровня СА невозможен .

Метод и основные результаты анализа

В наших работах каждое событие СКЛ , согласно моменту появления , сопоставлялось со сглаженным числом солнечных пятен на соответствующие сутки ( рис . 1). После этого суммировались события СКЛ , относящие к одному и тому же выбранному интервалу СА , и количество событий в интервале было поделено на суммарное время , в течение кото рого уровень СА находился в этом интервале . В итоге средняя частота событий СКЛ < ν >=< n >/ t оказалась

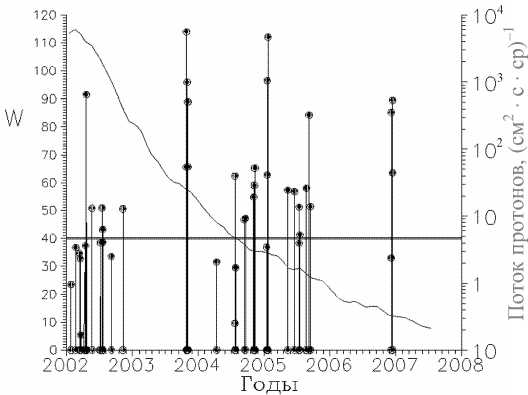
Рис . 1. Ход изменения уровня СА на спаде 23 цикла – плавная линия ( левая ось ординат ); моменты и величина пиковых потоков протонов СКЛ ( правая ось ординат ). Горизонтальная линия – уровень W =40 – разделяет перио ды активного и спокойного Солнца .

пропорциональной величине сглаженных чисел солнечных пятен < W > :

< ν ( ≥ F )>= K ( ≥ F ) ∙ < W >. (1)

При этом величина коэффициента K ( ≥ F ) зависит от выбранной пороговой величины F совокупности событий СКЛ .

Итак , первая закономерность гласит , что средняя частота событий СКЛ пропорциональна уровню солнечной активности . Другими словами , среднее количество событий СКЛ , которое появляется за заданный период времени , пропорционально сумме месячных ( или годовых ) чисел солнечных пятен за этот же период времени .

Вторая закономерность относится к функциям распределений событий СКЛ по их величине . Функ ция распределения – это зависимость частоты собы тий величиной ν ( ≥ F ) от величины событий F . Ока зывается , что функции распределения событий ин вариантны по отношению к солнечной активности . На рис . 2 приведены функции распределения для разных уровней ( периодов ) СА из работы [4]. Если поделить частоту ν W ( ≥ F ) на величину солнечной активности W , получим ( рис . 3)

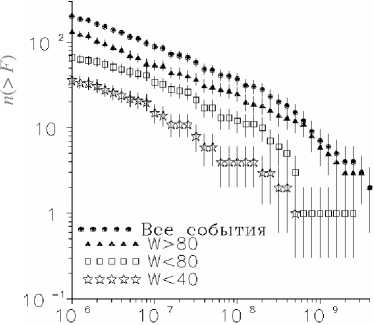
F протонов см

Рис . 2. Функции распределения событий по величине флюенсов для разных периодов СА ( отмечены на рисунке ).

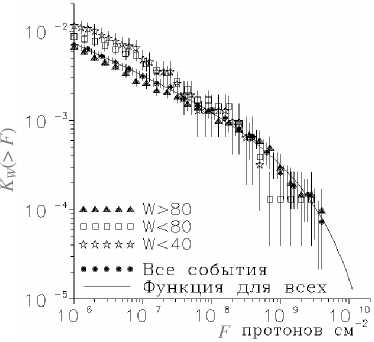
Рис . 3. Те же функции , нормированные к единичной солнечной активности .

(^v - ( ^ F_(>fA ----   Kw ⁽ ^ F ) .

Как видно из рис . 3, нормированные к солнечной активности функции распределения K_W ( ≥ F ) в пре делах статистических ошибок совпадают для всех уровней ( W ) СА . Небольшое расхождение K W ( ≥ F ) в области малых событий , скорее всего , обусловлено методическими ошибками определения частоты небольших событий в период большой солнечной активности , когда потоки частиц событий разной величины иногда налагаются друг на друга так , что маленьких событий не видно . Однако для нас важно совпадение функции в области больших событий СКЛ . Это означает , что доля экстремальных собы тий при всех уровнях солнечной активности одина кова и при низкой солнечной активности она та же , что и при высокой . То есть при малой солнечной активности вполне вероятно появление даже экс тремально больших событий СКЛ .

К такому выводу мы пришли уже в 1999 г . [8]. В дальнейшем нами была разработана модель потоков частиц СКЛ , в которой были установлены величины вероятности появления экстремальных событий в пе риод любой , в том числе и малой , солнечной активно сти [9, 10]. Одна из версий модели в 2001 г . стала Го сударственным стандартом России [11].

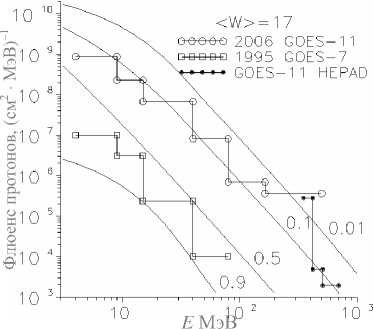
Рис . 4. Годовые флюенсы , измеренные на спутниках GOES ( ломаные линии ) в 1995 и 2006 гг . и вычисленные по модели энергетические спектры годовых флюенсов протонов , превышение которых ожидалось с вероятно стью 0.9; 0.5; 0.1 и 0.01 в годы со средним числом солнеч ных пятен < W > = 17.

Рассмотрим частный случай – вероятности появ ления разных флюенсов в годы , в которые среднее количество солнечных пятен было равно 17. Это годы 1995 и 2006. На рис . 4 приведены величины годовых флюенсов солнечных событий так , как они были измерены на спутниках GOES-8 и GOES-11, а также предсказанные моделью дифференциальные энергетические спектры флюенсов , превышение которых при данной СА ожидалось с вероятно стью 0.9; 0.5; 0.1 и 0.01. Из сравнения эксперимен тальных данных с модельными оценками следует , что превышение появившихся в 1995 г . флюенсов ожидалось с вероятностью около 0.7; а появив шихся в 2006 г . – с вероятностью 0.1. Это означа ет , что при подобном уровне СА (< W >=17) лишь в одном году из 10 ожидаются флюенсы , зарегист рированные в 2006 г . Это не является чем - либо исключительным .

Отметим еще , что в работе [4] нами было проде монстрировано , что так же , как периоды максимума и минимума СА , ничем не отличаются друг от друга и фазы роста и снижения СА .

Выводы

Показана несостоятельность мифа о преимущест венном появлении больших событий СКЛ в годы , предшествующие и последующие за максимумом СА [5–8], и ошибочность предположения о допустимости пренебрежения потоками частиц в моделях СКЛ [12, 13] в так называемые годы спокойного Солнца .

На основе установленных нами закономерно стей , относящихся к зависимости средней частоты появления событий от уровня СА и инвариантности функции распределения событий СКЛ относительно уровня и фаз измерения СА , была разработана веро ятностная модель флюенсов и пиковых потоков протонов СКЛ . Эта модель [9–11] позволила нам прогнозировать появление больших событий СКЛ в годы спокойного Солнца (Quiet Sun periods) 2005 и 2006, что , согласно другим известным моделям СКЛ [12, 13], отрицается .

Настоящая работа частично выполнена благода ря поддержке гранта РФФИ -06-02-16268 а .