Закономерности распределения напряжений в грунтовых основаниях внутрихозяйственных автомобильных дорог

Местные автомобильные дороги, расположенные в границах сельских поселений, предназначенные для транспортного обслуживания объектов по производству, переработке и сбыту сельскохозяйственной и иной продукции, а также внутрихозяйственные автомобильные дороги разделяются на две группы: магистральные и полевые. В соответствии с нормативным документом СП 99.13330.2016 при проектировании внутрихозяйственных магистральных дорог должно быть учтено требование по обеспечению круглогодичных транспортных связей с объектами сельскохозяйственной переработки, сельскохозяйственного производства и иного вида производства, а также с объектами социальной

инфраструктуры (объекты торговли, культуры и т. п.). Для обеспечения круглогодичного проезда дорожную одежду устраивают из материалов, хорошо сопротивляющихся воздействию транспортных средств и влиянию климатических факторов. Дорожная одежда передает нагрузку от автомобилей на нижележащие слои основания, рассредоточивая ее на большую площадь. Для этих целей эффективным инструментом является армирование конструктивных слоев геосинтетическими материалами, в том числе плоскими георешетками [1; 2]. В результате этого в земляном полотне возникают значительно меньшие напряжения и деформации.

Возникающие в дорожной одежде напряжения от колес автомобилей уменьшаются с глубиной. Процессы, протекающие при деформации грунтового основания, подчиняются общим закономерностям механики грунтов. При этом следует иметь в виду, что форма и площадь контакта, а также распределение давлений зависят от соотношения жесткостей грунта и шины. Для экспериментальной оценки механических свойств и анализа напряженно-деформированного состояния дорожных одежд и грунтовых оснований наиболее широко применяются штамповые испытания с использованием жесткого штампа круглой формы.

Объекты и методы

Рассмотрим задачу определения напряжений в грунтовом основании при действии на него круглого жесткого штампа радиусом R , загруженного сосредоточенной нагрузкой P . Расчетная схема представлена на рис. 1.

Грунтовые основания, с одной стороны, представляют собой зернистую среду, напряжения в которой определяют, используя математический аппарат механики грунтов. С другой стороны, для определения напряжений в грунтовых основаниях широко используется расчетная модель сплошной среды и математический аппарат теории упругости. В соответствии с теорией упругости давление на упругое полупространство, передаваемое жестким штампом, распределяется по закону квадратичной параболы:

q ( r ) =

P

2 nR^R ² - rr

Эпюра давлений (рис. 2) получена в результате точного решения задачи о вдавливании штампа в упругое полупространство. Решение задачи ‒ в цилиндрических координатах. Особенностью данного решения является то, что минимальное давление возникает под центром штампа, а под краем штампа давление бесконечно велико.

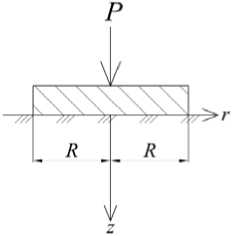
Рис. 1. Расчетная схема

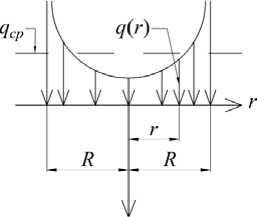
z

Рис. 2. Распределение давления на основание под жестким штампом

На практике обычно вместо точного закона распределения давления под жестким штампом используют приближенную равномерную зависимость:

= P q^cp = nR ^{2 .}

Эпюра давлений в этом случае имеет вид, представленный на рис. 3, а .

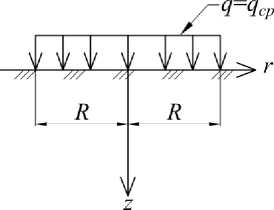
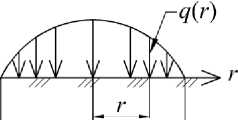
а                               б

Рис. 3. Распределение давления от жесткого штампа на грунтовое основание: а – равномерное; б – параболическое

Совсем иной вид имеет эпюра давлений на грунтовое основание, установленная экспериментально Фарбером [3] при надавливании круглым жестким штампом на основание из песка. Закономерность распределения давления под штампом имеет вид квадратичной параболы (3) и представлена на рис. 3, б :

q(r ) =2 q 1 - r- . к R 7

Определение напряжений по формулам теории упругости

Рассмотрим основные формулы теории упругости для вычисления главных вертикальных напряжений σ z под штампом в точках, расположенных по оси Z :

решение Буссинеска для случая равномерного распределения нагрузки [4]:

oz = q • 1 к

- 1.5 к

1+f R ^

к z 7

;

решение С.П. Тимошенко [5] для произвольного закона распределения нагрузки q ( r ):

R                        ..-5/2

o z = J 3 q ( r ) • rz ³ ( r ² + z ² )     dr ;                                 ।

Для постоянной нагрузки q(r) = q выражение (5) после интегрирования принимает вид o z = q

1 +------ z----:

(R2 + z2)

Для параболической нагрузки (3) выражение (5) после интегрирования будет иметь вид

2 qz3 Г 2 z3 (R2 + z2) + (R2 + z2 )15 •( R2 - 2 z2) R 2                 z3 (R2 + z2 )15

В работе американского профессора Роя Олсона [3] приведены формулы для определения напряжений под штампом в точках, расположенных на оси Z, при равномерном рас- пределении нагрузки:

o z = q 1 -

(1 + a2) n/2 J

и при параболическом распределении

^o z = ² q

D           D                2 - n

1 +-- a ²--- a" • (1 + a²) "

2 - n 2 - n

где a – переменная, определяется по формуле

z

a = —

R

На рис. 4 приведены экспериментально установленные данные о распределении напряжений под штампом, теоретически вычисленные по формулам (8) и (9).

При сравнении кривых распределения напряжений по глубине, вычисленных по формулам (4) и (7), оказалось, что формула (7) соответствует параболическому распределению (9) при n = 3, а решение Буссинеска (4) ‒ равномерному распределению (8) при n = 3.

Помимо формул теории упругости для определения напряжений в грунтовом основании как в сплошной среде имеется альтернативный подход. Он заключается в использовании математического аппарата механики грунтов. Рассматривая грунтовые основания как зернистую среду, Кандауров [6] предложил использовать следующие формулы для вычисления напряжений:

о z = q ■

° z = 2 q ■ i1 -

1 - exp

к

2 vz2 J

2νz2 R2

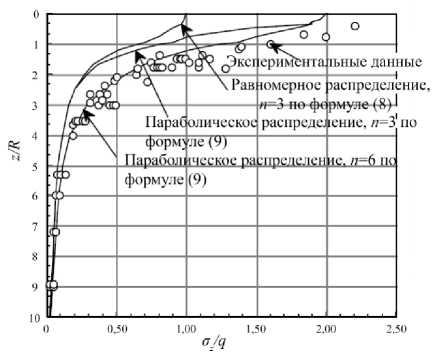
Рис. 4. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (8) и (9) [3]

1 - exp

_к 2 vz ² v

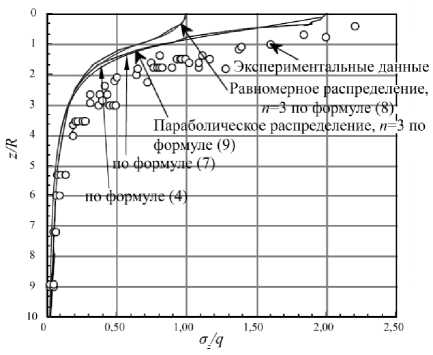
Рис. 5. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (4), (7), (8) и (9)

Таблица 1

Нормативные значения φ

Вид грунта	Разновидность	φ , град.
Песок	Крупный и гравелистый	38
	Средней крупности	35
	Мелкий	32
	Пылеватый	30
Глинистые грунты	Супесь	27
	Суглинок	22
	Глина	18
Скальные грунты	Известняк	33
	Туффиты и филлиты	28
	Порфиры	37

В механике грунтов основными механическими характеристиками, влияющими на распределение напряжений, являются угол внутреннего трения грунта φ и коэффициент бокового давления ν . В табл. 1 приведены нормативные значения угла φ для некоторых грунтов [7]. Видно, что угол φ изменяется в пределах от 18 до 38^о.

Г.И. Покровский, пользуясь методами статистической механики, установил связь между коэффициентом бокового давления ν 1 и углом внутреннего трения φ сыпучего тела:

V = 1 - 0,74 • tg ф .                                 (13)

В случае очень деформируемых обойм коэффициент бокового давления ν 2 очень близок к расчетному и определяется по формуле, предложенной Ренкиным:

V 2 =

1 - sin ф

1 + sin ф

В случае жесткой обоймы коэффициент бокового давления ν 3 рассчитывается по формуле, предложенной Жаки:

V ₃ = 1 - sin ф .

В табл. 2 приведены вычисленные по формулам (13)–(15) значения коэффициентов бокового давления ν 1 , ν 2 , ν 3 .

В соответствии с материалами монографии Г.К. Клейна [8] коэффициенты бокового давления для различных грунтов принимают значения, приведенные в табл. 3.

Таблица 2

Коэффициенты бокового давления, вычисленные по формулам (13) – (15)

φ , град.	38	35	32	30	27	22	18	33	28	37
ν 1	0,42	0,48	0,54	0,57	0,62	0,70	0,76	0,52	0,61	0,44
ν 2	0,24	0,27	0,31	0,33	0,38	0,45	0,53	0,29	0,36	0,25
ν 3	0,38	0,43	0,47	0,50	0,55	0,63	0,69	0,46	0,53	0,40

Сравнение формул Кандаурова (11), (12) при ν = 0,42 с экспериментальными данными показано на рис. 6. Из представленных графиков видно, что формула (12) соответствует параболическому распределению (9) при n = 3.

Результаты и их обсуждение

Метод экспоненциальной аппроксимации широко используется в дорожном строительстве. Например, в работах [9], [10] использована экспоненциальная зависимость в виде о z = B • exp (-YZ),                                 (16)

где B – константа, γ – коэффициент затухания по глубине.

В данной работе предлагается вместо выражения (16) использовать следующую зависимость для определения напряжений в точках, расположенных на глубине z :

о _z = 2 q [ exp ( v { 1 - ү_х z } ) ]⁽ 1 " ) ,                                 ⁽¹7)

где ν – коэффициент бокового давления грунта; γ 1 – коэффициент затухания, определяемый по результатам экспериментальных исследований.

Таблица 3

Коэффициенты бокового давления для типичных грунтов

Грунт	Коэффициент бокового давления ν для грунтов
	сухого	влажного	насыщенного
Пески	0,40	0,45	0,45
Суглинки	0,50	0,55	0,60
Глины	0,60	0,70	0,70

Таблица 4

Значения ν и γ 1

ν	0,2	0,3	0,4	0,5	0,6	0,7	0,8
γ 1	23	19,15	17,1	16,5	17,1	19,15	24

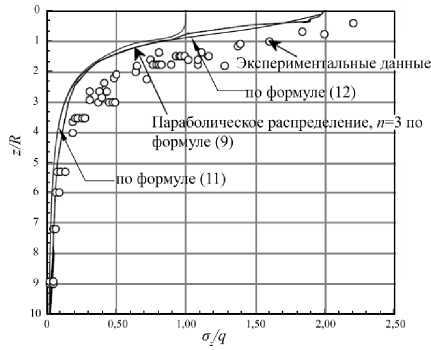
Рис. 6. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (9), (11) и (12)

В табл. 4 представлены значения γ1, вычисленные при различных значениях коэффициента бокового давления ν, изменяющегося в пределах от 0,2 до 0,8. Зависимости распределения напряжений σz по глубине, полученные в соответствии с формулами (16) и (17), представлены на рис. 7. Таким образом, имеется несколько формул для определения напряжений по оси симметрии жесткого штампа. Расчеты по этим формулам приближают- ся к экспериментальным данным, но все же дают заниженные значения напряжений на определенных глубинах. Экспоненциальная аппроксимация по формуле (16) также дает заниженные значения напряжений, поэтому эпюра напряжений имеет недостаточную выпуклость на интервале 0 < z/R < 4.

Наилучшее совпадение с результатами эксперимента для песчаного основания демонстрирует экспоненциальная зависимость (17), в которой вместо одного коэффициента затухания по глубине использованы две постоянные: коэффициент бокового давления грунта ν = 0,5 и экспериментально установленный для данного грунта коэффициент затухания γ 1 = 16,5.

Заключение

В настоящей работе предложена экспоненциальная зависимость изменения по глубине напряжений в грунтовом основании под жестким штампом. Отличительной особенностью данной зависимости является то, что вместо одного коэффициента затухания по глубине

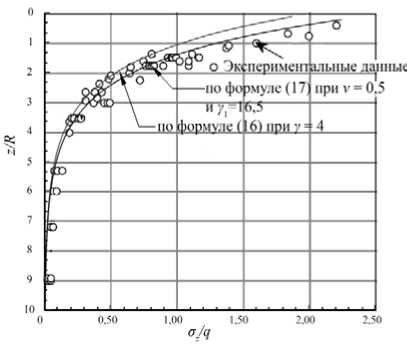
Рис. 7. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (16) и (17)

использованы две постоянные: коэффициент бокового давления грунта и экспериментально установленная для данного грунта константа. Использование предложенной зависимости позволяет более точно описывать напряженное состояние грунтовых оснований автомобильных дорог и применять для проектирования и конструирования дорожных одежд как внутрихозяйственного назначения, так и общего пользования.

S.A. Matveev , N.N. Litvinov, R.E. Petrov

Siberian State Automobile and Highway University, Omsk

Regularities of tension distribution in the intraeconomic highways soil base