Замечание о формулах для скорости волн Рэлея

Скорость волны Рэлея в задачах акустики однородных упругих сред может быть найдена с помощью выражения c_r = c_t £ = c_t4x , где x — единственный действительный корень, принадлежащий интервалу [0,1) , уравнения [1, с. 136]:

x ³ - 8 x ² + 8 x ( 3 - 2 u ² ) - 16 ( 1 - u ² ) = 0,                            (1)

где сделана замена x = £² и введены обозначения: и ² = ( c t/ c l )², c r , c t , c l - скорости поверхностных, поперечных и продольных волн соответственно.

Решение алгебраическим методом

Решаемое уравнение имеет вид f ( x ) = 0, где f ( x ) = ax ³ + bx ² + cx + d , a = 1, b = - 8, c = 8(3 - 2u 2 ) , d = - 16(1 - и ²). Дискриминант A = 4 b ³ d + b ² + c ² - 4 ac ³ + 18abcd - 27 a ² d ² = 128(128 u ⁶ - 340 u ⁴ + 502 u ² - 305) <  0 при u ² <  1,071, и, следовательно, уравнение имеет два комплексно сопряженных корня и один действительный.

Сделаем замену переменных x = y - b/3a = y + 8/3 , тогда уравнение (1) примет вид у ³ + py + q = 0, где p = - 8(6u ² - 1)/3, q = - 16(45 u ² - 17)/27 . Применим подстановку Виета у = z - p/ (3 z ), которая переводит уравнение в квадратное относительно z ³: z ⁶ + qz ³ - p ³/27 = 0. Получим ( z ³) 1, ₂ = ( - 9 q + 3з ^2 7 q ² - 4 p ³ )/18 и z k = ^( - 9 q + 33 27 7q ² - 4 p ³ )/18 exp ( i2 n k/ 3 ) , где к = 0,1,2 - номер корня. Запишем выражения для корней исходного уравнения:

xk

p 8  8  ₃ -9 q + л/3 ^27 q ² - 4 p³

— + - = - + ( ------ 2--------

3 z 3  3              18

exp ( i 2 п к/ 3 ) -    p exp ^{( -} i^{2 n k 3 ) 318}

3 3 - 9 q + ^^27q ² - 4 p³

Введем обозначения

T = 7((-64й27І07)й2^67)й271T, U± = 317 -45u2 ±3^T и запишем решения уравнения (1) в виде, аналогичном [2, см. (11)]:

8  2-          , ,_x xk = 3-3 U±exp(i2^^3) +

2(6 u 2 - 1) _z

---—---- exp ( - 12 n k /3)

k = 0,1,2.

Действительный корень уравнения (1) определяется этим выражением при к = 0:

2 _тт 2(6u ² - 1) - U₊ + —-----

3  ±     U+ где в выражении для U± выбор знака произволен.

Для случая «+» формула (3) получена Д. Нкемзи [2, см. (10)], а П.Г. Малишевским формулы (2) и (3) получены из более простых и удобных для вычисления выражений для корней уравне- ния Рэлея [2, см. (5) и (6); 3, см. (3) и (4); 4, см. (3)-(6)], которые, с учетом наших рассуждений, можно записать в обобщенном виде (ү = и2):

Һ 1 ( ү ) = 3^33 - 186 7 +321 7 2^ 192 / 3 ,

Һ2(ү) = -17 + 45/±Һ1(ү), Һ3(ү) = 17 — 45/±Һ1(ү), h4(/) = V6-Y, x (Y) = 2 [4 - 3Һ3(ү) + sign[ h4 (ү )]^sign[ h4(ү)] - h2 (/) ].                     (4)

Заметим, что в выражениях для Һ 2 ( ү ) и Һ 3 / ) выбор знака, как и в (3), на значение x не влияет. Связь между (3) и (4) устанавливается путем преобразований, аналогичных приведенным в [2]. При ү >  / 0 » 0,321498... [4], что соответствует переходу подкоренного выражения Һ ₁ ( ү ) к отрицательным значениям, корень остается действительным, так как в квадратных скобках суммируются комплексно сопряженные числа. Для случая выбора знака «-», выражение для действительного корня приведено и проанализировано в [5, 6]. Выражения (3) и (4) также можно использовать в аналитическом выражении для производной определителя Рэлея при нахождении вычета, приведенного в [6].

При численной реализации формул (3) и (4) в конкретной системе необходима проверка качества реализации функции извлечения кубического корня из комплексного числа и коррекция ее выбора корня при необходимости. Так, например, в одних системах ^-1 =- 1, в других - выбирается значение корня, лежащее в первой четверти (Re, Im >  0).

Решение с использованием тригонометрических и гиперболических функций

Запишем, следуя работе Г. Холмса [7], решение исходного уравнения f (x) = 0. Введем обо- значения:

^xN =

—

b 8

, = , , ^yN = f ^{( x}N ) =

3 a 3

16(17 - 45 и ²)

,    3ac - b

,

3 = i A =

32 3

- 1, h = 2 а д =----- (6 и

- 1)³², H = 2 a A ³

32^3(1 - 6 и )  .

В работах [7, 8] при использовании тригонометрических и гиперболических формул получены выражения для корней в трех случаях, которые реализуются для нашего уравнения на разных интервалах значения параметра u ² :

1) ^Re ( yN/h ) = 0: x = x_N

—

2 A sinh -sinh 3

- 1 1 ^yN

I H

, т. е.

842    2

x =---у 1 - 6 и Sinh

• 2)    yN/h >+ 1: x = Xn -

1  • п- 1

sinh

2 3 cosh -cosh 3

- 1 cosh

1 1 y N

I h

1 п- 1 cosh

• 3)    I y_N/h | <- 1: x = x_N + 2 5 cos -cos

1 1 y N

I h

x =---

- 1cos

cos

17 - 45 и ² 2^2(1 - 6 и ²)^3/2

, т. е.

17 - 45 и ² 2^(6 и ² - 1)^3/2

, т. е.

17 - 45 и ² 2^2(6и ² - 1)^3/2

при и ² <  16 ;

при 1/6 <  и ² <  и 2 ,

при и >  и ₀,

где и 2 = ү ₀ - 0,321498.... Формула (7) для уравнения (1) была впервые представлена в [9] и, как (5) и (6), не содержит кубических радикалов или интегральных выражений.

Построение приближенной формулы для вычисления корня уравнения Рэлея

Использование приближенных выражений оправдано при недостатке вычислительных мощностей для численного решения исходного уравнения или использования аналитического выражения ввиду его математической сложности, если их погрешность вычисления меньше заданной величины. Обыкновенно, приближенные формулы проще точных аналитических выражений, что позволяет быстро оценить необходимую величину или использовать простое программное обеспечение цифровых двойников и снизить требования к аппаратной части оборудования, сопровождающего технологические процессы.

Построение приближенных формул требует интуиции и опыта, например, по графику функции необходимо предложить комбинацию из приближающих ее элементарных функций или предложить преобразование функции и ее переменных для наилучшего ее такого приближения. Также формулы можно конструировать методами математического анализа: заменой переменных, линеаризацией исходного выражения или разложением в ряд по различным, например, ортогональным функциям и т. д.

Для оценки погрешности приближения будем использовать обычную формулу для относительной погрешности: δ = | f_точн - f_прибл | ⋅ 100 %/ f_точн , где f_точн , f_прибл – точное и приближенное значение соответственно.

П.Г. Малишевский в [10] предложил приближать функцию 4x полиномом третьей степени от коэффициента Пуассона σ = (2 γ - 1)/2( γ - 1) = (2 u ² - 1) 2( u ² - 1) . При использовании точной формулы (4) (со знаком «+») и метода наименьших квадратов была получена формула

4x ≈ 0,874027 + 0,195608 σ - 0,0425231 σ ² - 0,0569549 σ ³. (8)

Погрешность такого приближения не превышает 0,45 % на области определения и 0,1% при σ ∈ [0, 0,5] , в области [0, 0,2] относительная погрешность не превышает 0,0006 %. В качестве недостатка можно отметить быстрый рост погрешности вне интервала σ ∈ [0, 0,2] (см. рисунок).

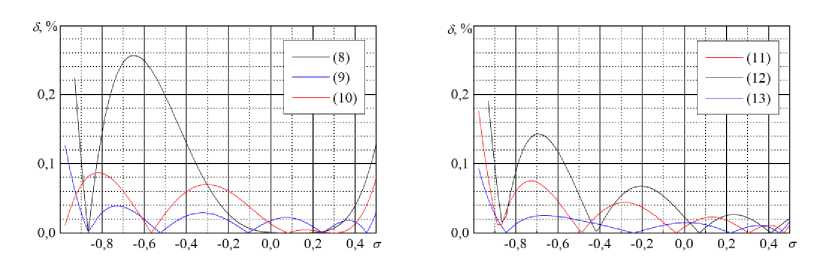
Зависимость погрешности приближенных формул (8)–(13) от коэффициента Пуассона σ

Поскольку для очень многих веществ коэффициент Пуассона находится в области [0, 0, 4] , а также за последние 100 лет было открыто много кристаллических и пористых материалов с отрицательными коэффициентами Пуассона, то можно поставить задачу об уточнении формулы. Будем дальше искать преобразование, которое приведет функцию к виду, который лучше приближается полиномом. Так, замечено, что если аргументом оставить σ , то обратная функция к экспоненте от x и обратные тригонометрические и гиперболические функции приближаются полиномом третьей степени с большим коэффициентом корреляции и меньшей дисперсией. Выбор пробных функций был обусловлен в том числе и видом выражений (5)–(7). По возможности будем минимизировать относительную погрешность в «рабочей» области σ ∈ [0, 0,4] и во вторую очередь – погрешность на всей области определения.

В результате численных экспериментов найдены следующие приближенные формулы:

4x ≈ exp( - 0,13481767 + 0,22245627 σ - 0,064405126 σ ² - 0,050681185 σ ³). (9) 4x ≈ exp( - 0,13450658 + 0,221488406 σ - 0,06617292 σ ² - 0,04966605 σ ³). (10) 4x ≈ sinh(0,78938470 + 0,14577804 σ - 0,034075524 σ ² - 0,035363364 σ ³). (11)

л/ x ≈ cos(0,50694159 - 0,39660365 σ - 0,057051772 σ ² + 0,040189213 σ ³) .        (12)

x ≈ tanh(1,3493561 + 0,82668967 σ + 0,43981743 σ + 0,11823013 σ ³) .          (13)

Формула (9) была получена логарифмированием функции а/ x ( σ ) и вычислением коэффициентов полинома третьей степени методом наименьших квадратов для σ ∈ [ - 1, 0,5] . Для уточнения формулы в раб очей области была попытка построить такую же формулу (10), но проходящую через точку v x (0, 3) и имеющую такую же первую производную в этой точке, что и у точной формулы. Минимизация происходила по первым двум параметрам, третий и четвертый – вычислялись по ним для соблюдения поставленных условий. Формулы (11)–(13) построены аналогично (9). Выражения с sin , cosh дают большую погрешность вычислений и не приведены.

Анализ погрешности приближенных формул показывает, что наименьшая погрешность (менее 0,0006 %) в диапазоне σ ∈ [0, 0,2] у самой простой формулы П.Г. Малишевского (8). Для использования в диапазоне [ - 0,5, 0,5] с погрешностью менее 0,02 % и в диапазоне [ - 0,9, 0,5] с погрешностью менее 0,03 % можно использовать приближенную формулу (13).

Заключение

Приведены алгебраическое и тригонометрическое решения исходного кубического уравнения, выраженные через квадрат отношения скоростей объемных волн. Алгебраическое решение получено в виде двух эквивалентных форм, которые сохраняются для всего исследуемого диапазона 0 ≤ u ² ≤ 0,75 . Решение, записанное через тригонометрические функции и их аналитическое продолжение – гиперболические функции, требует разделения исходного диапазона на три интервала, на которых оно определено различными выражениями. Однако оно не требует работы с комплексными числами и вычисления кубических радикалов. Можно предположить, что разнообразие форм записи точных решений может облегчить рассмотрение задач возбуждения и распространения поверхностных волн в аналитическом виде, построения новых приближенных формул для скорости волн Рэлея и задач дифракции.