Замечательные точки и линии треугольника в школьном курсе математики

Школьные знания о треугольниках считаются основополагающими в математике и обладают большой практической ценностью во многих областях человеческой культуры. Знание базовых теорем и свойств треугольников позволяет нам широко применять в профессиональной сфере и даже в жизни при решении повседневных задач.

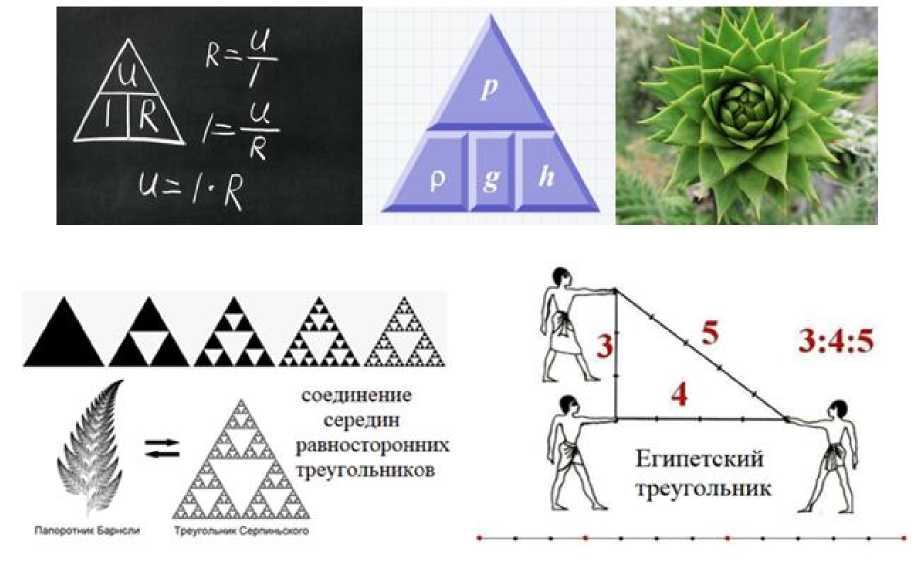
Рис. 1. Геометрическая форма треугольника вокруг нас

В первую очередь, знания о треугольниках позволяют нам рассчитывать и анализировать геометрические формы и кон- струкции вокруг нас (рис. 1). Будь то строительство домов, дизайн интерьера, создание компьютерных моделей или ар- хитектурных проектов – везде треугольники находят свое применение. Понимание теории треугольников помогает инжене- рам, архитекторам и дизайнерам создавать устойчивые и эстетически привлекательные конструкции (рис. 2).

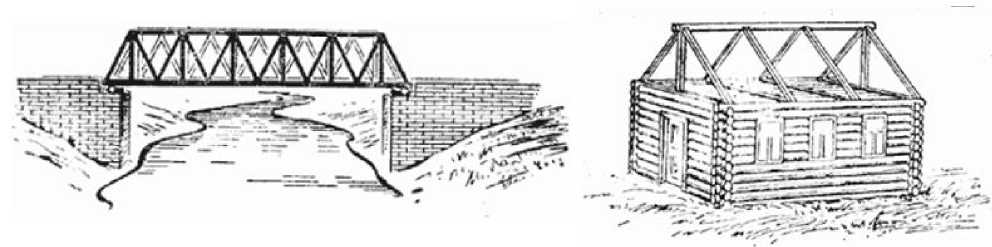
Рис. 2. Примеры архитектурных конструкций, использующих треугольники

Кроме того, школьные знания о треугольниках работают в области навигации и геодезии. С помощью тригонометрии, базирующейся на треугольниках, мы можем определить расстояние до удаленных объектов, вычислить углы и направления движения. Это особенно важно для моряков, летчиков и геодезистов, которые должны ориентироваться в пространстве и точно определять свое положение. Позна- вательный интерес школьников при изучении геометрии треугольника будет подкрепляться указанием на многообразие вариантов применения этой фигуры в различных профессиях: семантике, менеджменте (рис. 3) и т.д. Удивительны способы применения треугольника для иллюстрации геометрических противоречий и числовых закономерностей (рис. 4).

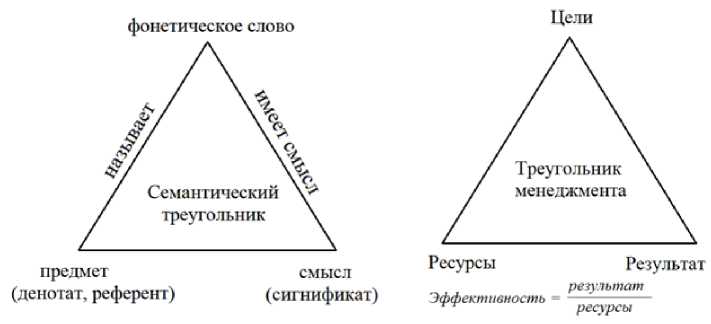
Рис. 3. Использование формы треугольника в семантике и менеджменте

Незаменимы знания о треугольниках в физике и строительной инженерии. Они позволяют нам анализировать и решать задачи, связанные с расчетом векторов сил и давлений. В медицине треугольники используются для определения угловой фор- мы частей тела, планирования операций и создания протезов. В робототехнике и автоматизации треугольники являются основой для расчета координат и движения различных механизмов.

Рис. 4. Иллюстрации в форме треугольника

Не только в научных и инженерных областях, но и в нашей повседневной жизни, знания о треугольниках имеют свою ценность, в том числе для интеллектуальных тренировок и оригинальных умственных развлечений. Например, при планировании маршрута путешествия или вычисления расходов на строительство забора, знание принципов треугольников позволит избежать ошибок и сохранить время и ресурсы.

Таким образом, школьные знания о треугольниках имеют не только теоретическую, но и практическую ценность. Они являются основой для понимания и анализа геометрических форм и конструкций, находят применение в научных, инженерных и медицинских областях, а также по- могают нам в повседневной жизни. Поэтому внимание, уделяемое треугольникам в школьной программе, является важным и необходимым для успешного функционирования в современном мире.

Треугольник – самая простая устойчивая фигура. В физике она моделирует абсолютно твердое тело (рис. 5). О сумме углов треугольника в разных метрических пространствах спорят мыслители. Решение треугольников – самая распространенная задача в школьной планиметрии, изобилующая многообразием всевозможных подходов к ее решению. На этом простейшем многоугольнике мы разбираем основные виды геометрических задач.

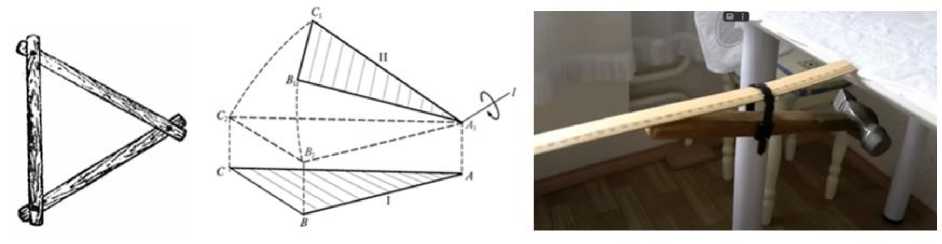
Рис. 5. Моделирование твердого тела с помощью треугольника в физике

В данной работе мы представим в компактном виде информацию об особо интересной части теории треугольника: его замечательных точках и линиях. Ни у какой иной фигуры нет такого разнообразия особенных точек и связанных с ними свойств. Изучение такой теории подарит истинное наслаждение интеллектуалам и способно заразить интересом к математике даже застарелых скептиков.

Мы опустим доказательства теорем и примеры решения задач. Наша цель – представить краткий учебный материал, на базисе которого легко разобраться в более подробной и полной его версии.

В данной работе рассмотрены следующие особенные («замечательные») точки треугольника:

• 1)    Ортоцентр (пересечение высот),

• 2)    Барицентр (центроид) – центр тяжести (пересечение медиан),

• 3)    Инцентр – центр вписанной окружности (пересечение биссектрис),

• 4)    Центр описанной окружности (пересечение медиатрис),

• 5)    Точка Жергона,

• 6)    Центр окружности девяти точек (Эйлера).

• 7)    Точка Лемуана.

• 8)    Точка Нагеля.

• 9)    Точка Торичелли.

С помощью этого перечня закрепим за каждой точкой в силу трудности первоначального их различения нумерацию.

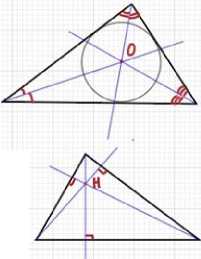
Точка пересечения биссектрис центр вписанной в треугольник окружности

Точка пересечения высот или их продолжений - ортоцентр треугольника

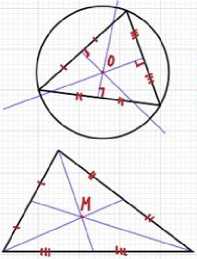
Точка пересечения медиан -центр тяжести (центр масс) треугольника или центроид

Точка пересечения серединных перпендикуляров - центр описанной возле треугольника окружности

Рис. 6. Наиболее известные замечательные точки треугольника

Эти точки используются в задачах на доказательства удивительных совпадений – особых свойств их взаимного расположения.

На одной прямой лежат точки:

• -    2, 3 и 8.

Точка 2 делит отрезок между точками 3 и 8 в отношении 2:1 (рис. 7).

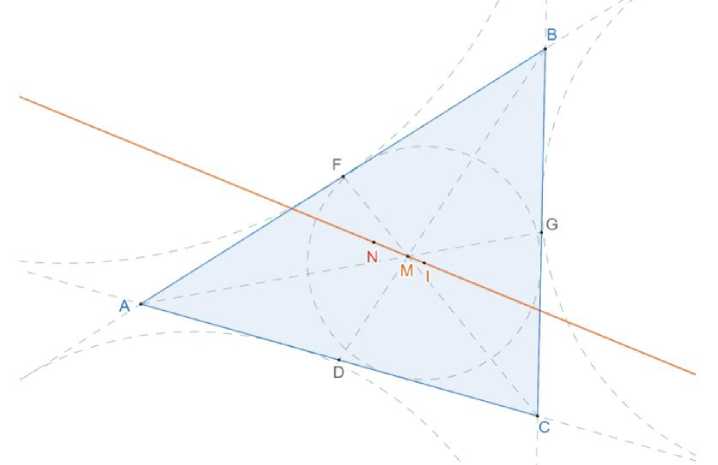
Рис. 7. Взаимное расположение точек 2, 3 и 8 на прямой

- 1, 2, 4 и 6 (на прямой Эйлера). При этом точка 6 лежит посередине между точ- ками 1 и 4 (рис. 8).

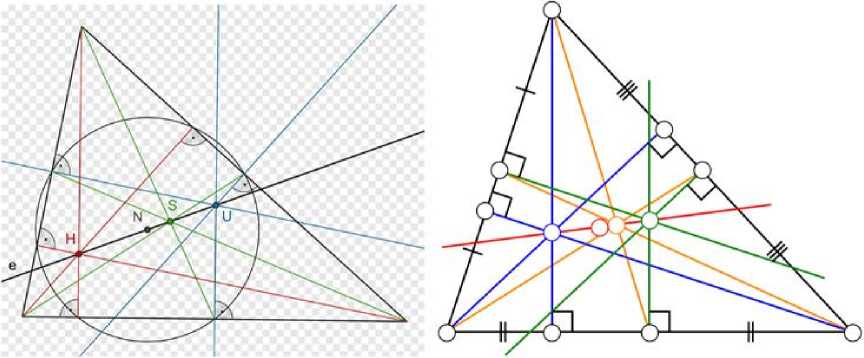
Рис. 8. Взаимное расположение точек на прямой Эйлера

Замечательными линиями треугольника называют биссектрисы, высоты, медианы, чевианы и медиатрисы (серединные перпендикуляры).

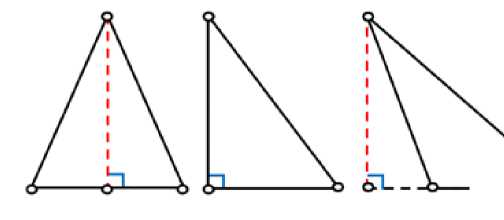
1. Ортоцентр Высоты треугольника перпендикулярны прямым, на которых лежат его стороны. Существует три различных варианта расположения высоты в треугольнике (рис. 9).

А К К / । \     \     1 \ X Z—«^—X Ь---X kk.X---X Высота в треугольниках различного типа

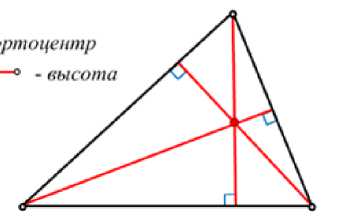
• - ортоцентр       / \ °   ° - высота У^\   \

Рис. 9. Высоты треугольника и точка их пересечения

2. Барицентр Барицентр (или центроид) – это геометрический центр плоской фигуры, положение которого в общем виде задается ради- J r • dV r = V       . ус-вектором: b

В физике положение барицентра плоской фигуры можно определить экспериментально с помощью отвеса (рис. 10).

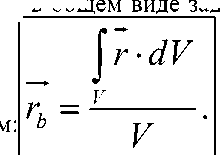
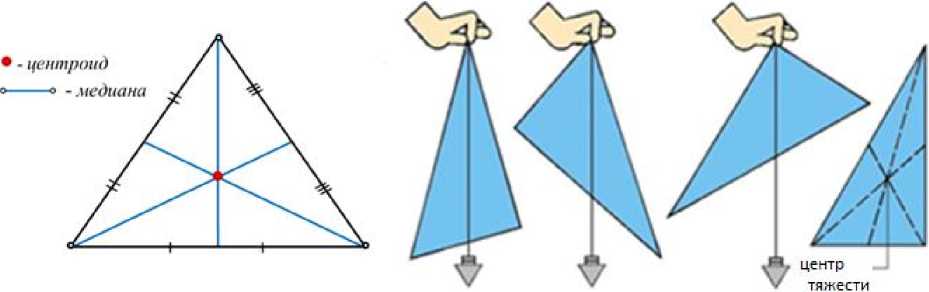
Рис. 10. Положение барицентра в геометрии и физике

В случае плоской фигуры отдельно определяются абсцисса и ордината барицентра фигуры. Примечательно то, что медианы треугольника делят его на шесть равновеликих треугольника, т.е. на шесть частей с равными площадями. Эти знания позволяют решать очень интересные междисциплинарные задачи (рис. 11).

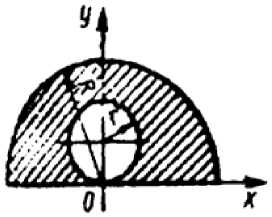
Определить координату центра тяжести у_с заштрихованной площади фигуры, если даны радиусы окружностей: R = 0,99 м, г = 0,33 м. (0,446)

Рис. 11. Задача на межпредметные связи геометрии и физики.

Если изготовить из однородного вещества предмет данной формы, то барицентр укажет положение точки опоры, при которой тело будет находиться в равновесии во внешнем однородном гравитационном поле (рис. 5 справа). Поэтому в физике термин «барицентр» – синоним понятия «центр масс». Экспериментально его положение определяется с помощью отвеса (рис. 10).

В треугольнике барицентр лежит в точке пересечения его медиан. Медианы треугольника являются его чевианами, т.е. отрезками, соединяющими вершину треугольника с некоторой точкой на противоположной стороне. Для чевиан работает теорема Чевы, установленная итальянским инженером в 1678 году: если в треугольнике АВС чевианы пересекаются в одной точке, то произведение последовательных отношений равно единице (рис. 12).

• • Если в треугольнике ЛВС пря пересекаются в одной точке, то АК BL СМ

КВ LC МА

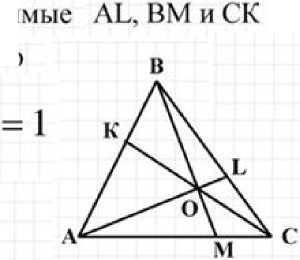
Рис. 12. Признак пересечения чевиан в одной точке

В треугольнике барицентр лежит в точке пересечения его медиан. Медианы треугольника являются его чевианами, т.е. отрезками, соединяющими вершину треугольника с некоторой точкой на противоположной стороне. Для чевиан работает теорема Чевы, установленная итальянским инженером в 1678 году: если в треугольнике АВС чевианы пересекаются в одной точке, то произведение последовательных отношений равно единице (рис. 12).

Эта теорема самим автором была доказана с помощью геометрии масс . Сегодня известны еще несколько иных вариантов ее доказательства. Рассмотрение способов доказательства этой красивой теоремы помогает развитию творческого подхода к решению математических задач.

С помощью теоремы Чевы можно доказать, что:

• 1)    три медианы треугольника пересекаются в одной точке (барицентр);

• 2)    три биссектрисы треугольника пересекаются в одной точке (инцентр);

• 3)    три высоты треугольника пересекаются в одной точке (ортоцентр). Пример доказательства приведен на рис. 13.

У барицентра треугольника есть два особых свойства :

• 1)    Проведенные через него чевианы разделяют своими концами стороны треугольника на шесть отрезков. И произведение длин трех из них, не имеющих общих концов, максимально.

• 2)    Сумма квадратов расстояний от центроида треугольника до его вершин принимает наименьшее значение (теорема Лейбница).

  
  
  

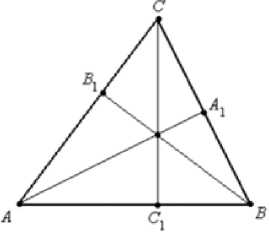
Из теоремы Чевы следует, что три высоты остроугольного треугольника пересекаются в одной точке.

Доказательство. Пусть в остроугольном треугольнике АВС точки Au Si, Ci лежат на сторонах ВС, АС и АВ соответственно (рис.). Прямоугольные треугольники AAiC и ВВ\С подобны по СА, СА двум углам, поэтому —- =--.

ВС ВС

Аналогично из подобия прямоугольных треугольников АА\В и СС\В, ВВ\А и СОЛ следует, что верны равенства:

ВС, ₌ ВС АВ, ₌ АВ А,В АВ ' С,А СА '

Перемножив зри полученные равенства, получим: АС, ВА, СВ, _ С,В А,С В,А '

Рис. 13. Применение теоремы Чевы к ортоцентру треугольника

3.    Инцентр.

Биссектрисы треугольника пересекаются в одной точке, называемой инцентром – центром вписанной в треугольник окружности (рис. 14).

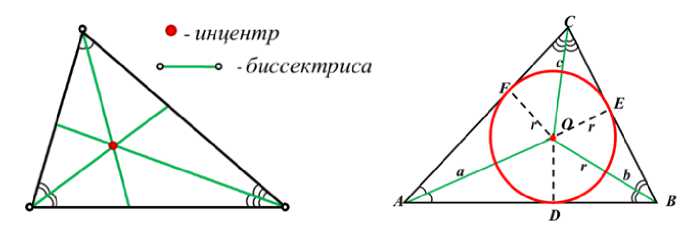
Рис. 14. Инцентр есть центр вписанной окружности

4.    Центр описанной окружности.

Центр описанной окружности треугольника лежит на пересечении его медиат-рисс . Серединный перпендикуляр (меди-атрисса) отрезка – это геометрическое место точек, равноудаленных от его концов. Интересно, что эта точка расположена внутри остроугольного треугольника, вне тупоугольного, а у прямоугольного совпадает с серединой гипотенузы.

• 5.    Точка Жергона

• 6.    Центр окружности девяти точек.

Еще одна замечательная точка треугольника – точка Жергона – это точка пересечения отрезков, соединяющих вершины треугольника с точками касания вписанной окружностью противоположных сторон.

В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера» (рис. 8).

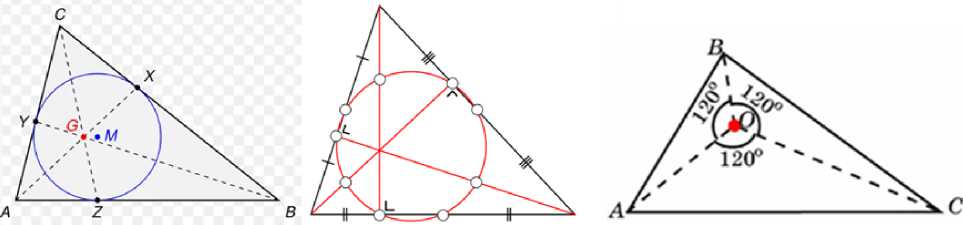
Б.ТочкаЖергона        6. Центр окружности девяти точек.       9. Точка Торричелли.

Рис. 15. Замечательные точки 5, 6 и 9

Эйлеру также принадлежит теорема: середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности . Эта окружность получила название «Окружность девяти точек» (рис. 15).

7.    Точка Лемуана. Сопряжения точек.

Изогональное сопряжение – геометрическое преобразование, при котором чевиана отображается относительно биссектрисы, выходящей из той же вершины. Симедиана – это прямая, симметричная медиане относительно соответствующей биссектрисы.

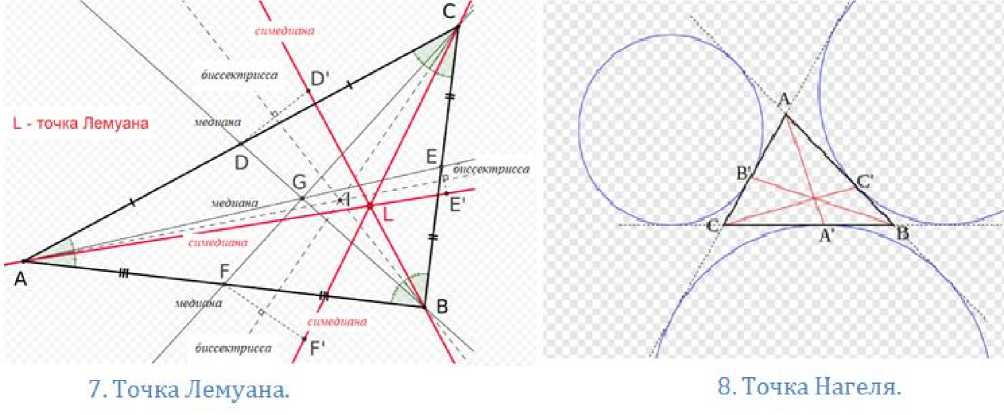
Рис. 15. Замечательные точки 7 и 8

Симедианы пересекаются в точке Лемуана (рис. 15). Удивительным свойством этой точки является следующее положение. Если спроецировать эту точку на сто- роны треугольника, опустив из нее перпендикуляры, то получим треугольник, барицентр которого как раз совпадет с точкой Лемуана. Другими ее свойствами являются:

• 1)    сумма квадратов расстояний от нее до сторон треугольника минимальна;

• 2)    она расположена от сторон треугольника на расстояниях, пропорциональных этим сторонам.

Пары изогонально сопряженных точек:

• -    точки 2 и 7: барицентр и Лемуана,

• -    точки 1 и 4: ортоцентр и центр описанной окружности.

В математике еще рассматривается изо-томическое сопряжение – симметричность чевиан относительно середин соответствующих сторон. Известны следующие пары изотомически сопряженных точек:

• 1)    точка Жергона и точка Нагеля,

• 2)    точка Лемуана и точка Брокара,

• 3)    точка барицентра изотомически сопряжена самой себе.

8.    Точка Нагеля. 9.    Точка Торричелли.

Точка Нагеля – это точка пересечения чевиан, соединяющих вершины треуголника и точки касания сторон треугольника с соответствующими вневписанными окружностями (рис. 15).

Точкой Торричелли треугольника (рис. 16) называется точка, из которой три луча, направленные в вершины треугольника, образуют между собой углы в 120⁰. Эта точка была открыта в ходе решения транспортной задачи. Как соединить имеющиеся города дорогами так, чтобы их длина была наименьшей? Или в геометрической формулировке: Как связать данное множество точек на плоскости самой короткой системой «дорог»? Такая система дорог называется сетью Штейнера . По таким сетям проектируются не только дороги, но и линии электропередачи и иные пространственные связи.

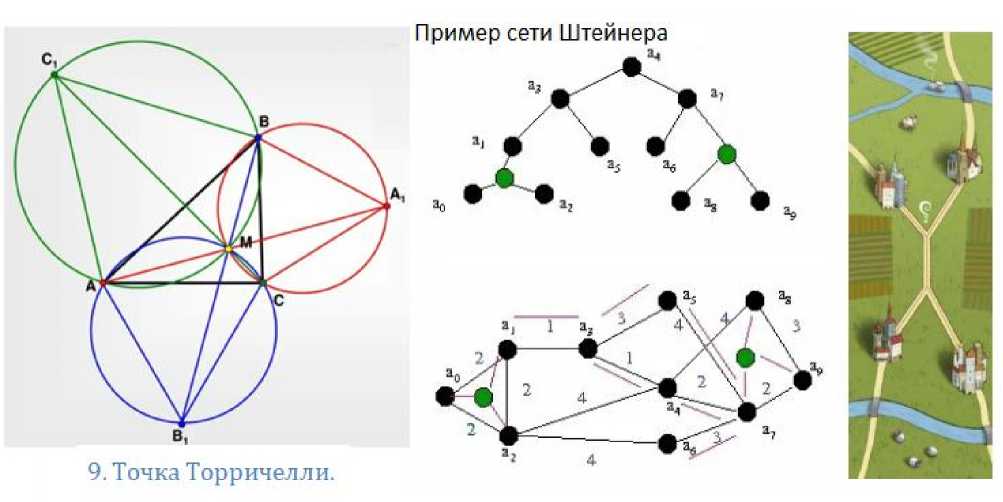
Рис. 16. Точка 9 и сеть Штейнера по расчету геометрии дорог

В применении к треугольнику она звучит так: найти точку, сумма расстояний от которой до вершин треугольника наименьшая .

Если взять центр описанной окружности, то для него справедливо свойство минимума наибольшего расстояния до вершин, а не их суммы. Если же взять бари- центр, то он даст минимум суммы квадратов расстояний. В 1659 году ученик Галилея итальянский физик и механик Винченцо Вивиани издал книгу «О максимальных и минимальных значениях», где описал новую точку – точку Торричелли. Эта точка лежит внутри треугольника и имеет много интересных свойств. Если у тре- угольника все углы меньше 1200, то у него есть такая точка. Есть и другие точки Торричелли. Мы на них не останавливаемся, так как это выходит за рамки школьного курса математики.

В заключение приведем цитату академика В.И. Арнольда из его статьи «О пре- подавании математики», где он пишет: «Математика – часть физики… В середине двадцатого века была предпринята попытка разделить математику и физику. Последствия оказались катастрофическими. Выросли целые поколения математиков, не знакомых с половиной своей науки и, естественно, не имеющих никакого представления ни о каких других науках. Они начали учить своей уродливой схоластической псевдоматематике сначала студентов, а потом и школьников…». Поэтому именно для полноценного воспитания учащих- ся на материале математики важно показывать ее связь с практическими задачами, а для этого просто необходимо привлекать материал из различных наук, совершенствуя межпредметные связи в полученных школьных знаниях.