Замкнутые решения динамических задач связанной термоупругости для цилиндра и шара
Автор: Жигалин Александр Григорьевич, Лычев Сергей Александрович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 2 т.4, 2011 года.
Бесплатный доступ
Получены замкнутые решения линейных задач связанной термоупругости для конечного цилиндра и шара. Решения построены в виде разложений по системам собственных функций дифференциальных операторов, порождаемых рассматриваемыми начально-краевыми задачами. Выделен класс граничных условий и симметрий, при которых решения задач термоупругости для тел канонических форм находятся без привлечения численных методов. Это позволило использовать построенные решения для изучения степени влияния связанности температурного и механического полей на их распределения во времени в зависимости от размеров рассматриваемого тела. Проведено сравнение полученных решений с решениями соответствующих задач теплопроводности. Показано, что для тел микронных размеров амплитуда температурных волн, образующихся вследствие взаимовлияния теплового и механического полей, заметно увеличивается по сравнению с амплитудой аналогичных волн в макротелах и составляет несколько процентов от величины начального температурного воздействия.
Связанная термоупругость, несамосопряженные операторы, аналитические решения, тела микронного масштаба, оценка влияния связанности
Короткий адрес: https://sciup.org/14320551
IDR: 14320551 | УДК: 539.3
Текст научной статьи Замкнутые решения динамических задач связанной термоупругости для цилиндра и шара
приближении уравнение движения содержит слагаемое, пропорциональное градиенту температуры. Этим учитывается влияние неравномерного нагрева тела на возникающие в нем деформации и напряжения. Уравнение теплопроводности линейной модели термоупругости включает слагаемое, пропорциональное скорости относительного изменения объема (скорости дилатации), которое отражает тот факт, что изменение объема тела приводит к перераспределению в нем тепла. Обычно дилатационное слагаемое влияет на температуру столь незначительно, что им можно пренебречь. Тем самым решение задачи существенно упрощается, поскольку уравнение теплопроводности без дилатационного члена оказывается не связанным с уравнением движения и может решаться независимо от него. Задачи, в которых дилатационное слагаемое не принимается в расчет, рассматриваются в теории температурных напряжений.
Представляет интерес определение условий, при которых дилатационное слагаемое начинает играть заметную роль в распределении температуры и перемещений в сплошной среде, то есть условий, при которых задачу необходимо решать в связанной постановке. Первые исследования на эту тему, по-видимому, относятся к 50–60-м годам предыдущего столетия. Вопросом в разной степени занимались P. Chadwick, B.A. Boley, J.H. Weiner, J.N. Sneddon, D.S. Berry [1]. Из более поздних работ следует отметить статью Ю.Э. Сеницкого в области динамических реакций термоупругих тел [2].
В настоящее время активно развиваются численные методы решения задач термоупругости. Тем не менее, слабые эффекты, например связанность термомеханических полей, могут быть изучены достоверно лишь на основе аналитических решений, получение которых в большинстве случаев представляет значительные математические трудности. Для их преодоления приходится вводить различные упрощающие предположения, например, рассматривать задачу для бесконечного или полубесконечного тела. При исследовании решений таких задач было установлено, что связанность полей деформации и температуры практически не отражается на их распределении в рассматриваемом теле. В этих случаях учет связанности представляет лишь теоретический интерес, поскольку объясняет диссипацию механической энергии и затухание упругих волн. Так, В. Новацким отмечено [3], [4], что решения, полученные в рамках термоупругости, незначительно отличаются от решений теории температурных напряжений. Значимость связанной термоупругости заключается в качественном эффекте затухания упругих волн, в «познавательной основе и общности этой теории».
Анализ уравнений линейной термоупругости в безразмерном виде дает основание предположить, что степень влияния дилатационного слагаемого должна зависеть от характерного размера рассматриваемого тела: влияние должно усиливаться при уменьшении размеров тела вплоть до микромасштабов. Поскольку гипотеза о сплошности среды применима, по-крайней мере, до размеров порядка 10 - 7 м (размеры атомов и межатомных расстояний в твердых телах имеют порядок 10 - 10 м), подобные задачи допустимо решать в рамках теории термоупругости. Чтобы при этом исключить влияние вычислительной погрешности на результаты расчетов, необходимо иметь метод решения, пригодный для тел конечных размеров и гарантирующий сходимость.
В работах [5], [6] предложен метод получения решений для начально-краевых задач, определяемых несамосопряженными дифференциальными операторами, в виде разложений по системе собственных и присоединенных функций полиномиального операторного пучка. Показано, что коэффициенты разложений определяются точно, их значения не зависят от количества удерживаемых в разложении членов. В этом смысле получаемые решения являются замкнутыми.
В настоящей статье авторы ставят цели: исследовать, как меняется вклад дилатационного слагаемого задачи термоупругости в распределение температуры и перемещений в зависимости от размеров тела; установить, когда пренебрежение дилатационным членом недопустимо для получения достоверного решения.
-
2. Начально-краевая задача связанной термоупругости
Пусть V — тело конечных размеров. Материал тела предполагается изотропным, а определяющие соотношения — линейными. Связь напряжений σ с перемещениями u и приращением температуры 0 = T - T r устанавливается законом Дюгамеля-Неймана:
о = p ( V u + ( V u ) ) + ( XV • u - y0 ) E .
Здесь T — текущая температура, T r — отсчетная температура, ц и X — упругие модули Ламе, соответствующие изотермическому процессу деформирования, V — оператор Гамильтона, символ « * » означает операцию сопряжения, у = а (3 Х + 2 ц ) — термомеханическая постоянная, а — коэффициент линейного теплового расширения, E — единичный тензор. Под отсчетной температурой понимается температура натуральной отсчетной конфигурации, при которой деформации и напряжения в теле полагаются равными нулю (естественное состояние).
Тепловой поток q пропорционален градиенту температуры согласно закону Фурье:
q=-ЛV0,
где Л — коэффициент теплопроводности.
Полная система уравнений термоупругости получается из уравнения движения
Г - 92u V • о + pf = р—-5t2
и уравнения теплового баланса
T — = -V- q + to, dt где p — плотность массы, f — массовые силы, t — время, s — объемная плотность энтропии, to — мощность внутренних источников тепла, отнесенная к единице объема.
Разложение свободной энергии Гельмгольца в ряд Тейлора с точностью до слагаемых второго порядка малости дает выражение для плотности энтропии s в следующем виде:
0s = yV • u + к—.
Т
r
Здесь через к обозначена теплоемкость единицы объема.
Соотношения (1)–(4) с учетом последнего равенства приводят к системе уравнений линейной термоупругости в перемещениях [3]:
<
pAu + (X + ц)V(V • u) - yV0 + pf = р
5 2u
5 1 2
A0
1 £0
a 51
Y T r d
Л 51
( V* u ) + to = 0,
где A = V •V — оператор Лапласа, a = Л / к — коэффициент температуропроводности.
В динамических задачах поля деформации и температуры оказываются взаимосвязанными, в отличие от задач статики и теории температурных напряжений. Слагаемое yV0 в первом уравнении системы (5) определяет влияние неоднородного поля
Y T 5 , .
—L—( V ■ u ) во втором Л 5 t
температуры на деформацию тела. Наличие дилатационного члена уравнении системы означает, что объемное расширение приводит к перераспределению теплоты в теле, причем этот процесс зависит от скорости объемного расширения.
Исследование качественных особенностей решения удобнее проводить с использованием безразмерных величин. Пусть l — некоторый характерный размер тела. Тогда безразмерные величины могут быть представлены следующим образом:
- r r = l ,
- 0 ——
,, l T r
tc t = .
l
Здесь r — радиус-вектор места, c = ^/( Х + 2 р)/р — скорость продольной волны в материале.
В безразмерных переменных оператор Гамильтона примет вид: V = lV , а оператор Лапласа: Д = V ■V = l 2 Д . С учетом этого исходная система уравнений (5) может быть записана в следующем виде:
<
Д й + A V ( V^ u ) - B V0 + f = ( A + 1)
5 2u
5 t 2 ,
soД0- C— 5 t
-
5 ~
D d (V ■ u) + ro = 0, 51
где безразмерные коэффициенты A , B , C , D вычисляются по формулам
f =^ f ,
p
l 2
го = —
Граничные условия в общем виде могут быть записаны в безразмерных переменных следующим образом:
B 1 ■ ( n ■ й )| д V = B 2 ■ u I d V
61П ■ q |dV = b20 |dV , где вид тензоров B 1, B 2 и констант b1, b2 зависит от конкретной задачи.
Определяющие соотношения (1), (2) примут вид
*
(Г = V ui + (v ui) +[( A - 1)V^ й - B 0] E, q = V0.
Таблица. Значения безразмерных коэффициентов для некоторых материалов при T r = 293 K
|
Коэффициент |
Материал |
||
|
Алюминий |
Алмаз |
||
|
Медь |
|||
|
A |
2,77778 |
3,125 |
1,16279 |
|
B |
0,0492045 |
0,0407343 |
0,000874912 |
|
C |
6,89 1 45 - 107 l |
3,72 7 3 7 - 107 l |
3,18415 - 107 1 |
|
D |
12 , 915 - 107 l |
6,38 1 81 - 10 7 l |
2,87 7 86 - 107 1 |
Аналогичным образом в безразмерных переменных могут быть поставлены начальные условия:
u 1 t=0 = u 0 ,
Su , ^=0 = v 0 , ®U = @ 0 .
d 1
Далее для краткости знак «~», подразумевающий безразмерные величины, везде опускается.
В отличие от коэффициентов A и B первого уравнения системы (6) безразмерные коэффициенты C и D второго уравнения обуславливаются не только свойствами материала, но и характерным размером l . Это означает, что в зависимости от размера тела связанность полей деформации и температуры проявляет себя в разной степени. В Таблице приведены значения безразмерных коэффициентов при T r = 293K для трех материалов: алюминия, меди и алмаза [7]. Легко видеть, что для тел масштаба 10 7 м все коэффициенты системы (6), кроме коэффициента B при градиенте температуры, будут иметь один и тот же порядок. Расчеты, которые приводятся в настоящей статье, показывают, что связанность становится заметной уже при размерах тел порядка 10 - 6 м.
-
3. Построение замкнутого решения
В работе [5] изложена общая теория построения замкнутых решений начальнокраевых задач, содержащих производные по времени любого порядка. Решение отыскивается в виде разложения по базису гильбертова пространства функций, интегрируемых с квадратом. В качестве элементов базиса используются собственные и присоединенные функции полиномиального пучка дифференциальных операторов [8, 9], порождаемого начально-краевой задачей. Общая форма такого представления решения также приводится в [5]. Следует особо отметить, что в задаче связанной термоупругости с параболическим уравнением теплопроводности спектр операторного пучка прост [10], поэтому используемый базис не содержит присоединенных функций, что существенно упрощает построение решения рассматриваемой задачи.
Задача (6)–(8) может быть записана в операторной форме:
H [ x ]= g ,
G [ x ]| a v = 0 , । d x.
x | t =0 = x 0 , "Д7 1 1 =0 = x 0 .
О 1
Дифференциальное выражение оператора H определяется системой уравнений (6); G есть оператор краевых условий, соответствующий соотношениям (7) ; x = (u, @) — искомая четырехкомпонентная вектор-функция; g = -(f, го) — заданный вектор внешних воздействий; x0 = (u0,00) — начальные значения; X0 = (v0,0) — начальные скорости. В качестве компоненты 0 |t=0 начальной скорости X0 можно принять любое значение. Поскольку дифференциальные уравнения модели содержат производные температуры по времени лишь первого порядка, эта величина не входит в результирующие формулы. Для определенности принято 0 | t=0 = 0.
Дифференциальный оператор H действует в гильбертовом пространстве L 2 интегрируемых с квадратом 4-компонентных вектор-функций, скалярное произведение в котором задается следующей формулой:
-
< f i , f > = J^ / 1 J 2 dV ,
V i =1
где f 1 i , f 2 i — компоненты вектор-функций, а черта над символом означает операцию комплексного сопряжения.
Введенный таким образом оператор H можно представить в форме, позволяющей отделить дифференцирование по пространственным переменным от дифференцирования по времени:
-
h = H + H + H . 0 1 5 t 2 5 t2
Здесь H 0, H 1, H 2 — пространственные дифференциальные операторы с общей областью определения, заданной условиями (9), имеющие блочную структуру:
A + A grad div - B grad v 0 A J
H 0
2 0 0 > , H = 2- ( A + 1) E 0 > .
(- D div - C J 2 ( 0 0 J
Разложение искомой вектор-функции по базису пространства L 2 может быть записано в виде:
-
x = & i ( t Mr ).
i =0
Базисные функции y i ( r ) должны удовлетворять граничным условиям и уравнению
H,i[yi] = 0, где H представляет собой квадратичный пучок дифференциальных операторов [10]: ^ i
H , i = H 0 +^ Z H 1 +^ 2 H 2 .
В развернутой форме краевая задача относительно функций y i = ( k i , 0 i ) формулируется следующим образом:
Ak + AV(V • k) - BVO = (A + 1)^2k,
AO- C EO- D E(V- k ) = 0,
B 1 - ( n - ° ) | g V B 2 - k | a V , & i n - q I d V b 2 O I d V .
Задача (10)-(11), в соответствии с терминологией [11], будет называться обобщенной задачей Штурма-Лиувилля. Вектор-функции ( k i ( r ), O i ( r ) ) , являющиеся ее нетривиальными решениями, есть собственные функции, а E i — собственные значения дифференциального оператора термоупругости, порождаемого исходной задачей. Для получения конечных и не зависящих от количества членов в разложении выражений для координатных функций ф i ( t ) необходимо использовать собственные функции у * = ( k * , O * ) сопряженного дифференциального оператора. В [5] приводятся соотношения обобщенной биортогональности, которым удовлетворяют собственные функции рассматриваемой пары взаимно сопряженных операторов:
0, / * j ; \ N . , / = j ,
0, / * j ;
_ M, i = j .
( H^- , y j ) + (^ j H 2 у . , y j )
< и 2 У / , У * )-^Л 7 < Н 0 у , у^
В дальнейшем для проведения вычислений используется первое из соотношений биортогональности как менее громоздкое.
Операторный пучок, сопряженный с HE , в общем виде определяется следующим ^/ выражением:
H i = и 0 + e h * +^2 и 2 .
Использование теоремы Гаусса-Остроградского позволяет получить явный вид сопряженного оператора:
и ;
= " A ■ A grad div - ( A + 1) ^ i2 D E i grad'
v Bdiv A-CEi )’ причем операторные коэффициенты сопряженного пучка записываются следующим образом:
A + A grad div 0 v B div Av

*
' 0 D grad ' v 0 - C ,
h2
f-(A + 1)E 0)
v 0 0 v
= H 2 .
Очевидно, что HE * H* , то есть оператор, порождаемый задачей термоупругости, Е/ Е/ является несамосопряженным. Краевые условия оператора H, накладывают
Е/ определенные ограничения на краевые условия сопряженного оператора H* . При этом
Е/ краевые условия обоих операторов должны быть такими, чтобы системы собственных функций каждого из них служили базисами в пространстве L2. Если ввести обозначения:
v = Vk, + (Vk, )* + [(A - 1)V • k, - B6JE, a*, = Vk* + (Vk* )* + [(A - 1)V- k* + D^6* ] , то в качестве граничных условий, обладающих требуемыми свойствами, могут использоваться, например, следующие условия:
-
- для теплоизолированной, свободной от внешних сил границы
д6.
п • а , | д v = 0 , —L |д v = 0 — в задаче (10)-(11);
д п
* дО/ п • аi |дV = 0, —L |дV = 0 — в сопряженной задаче;
д п
-
- для теплоизолированной границы, закрепленной в направлении нормали и свободной от касательных напряжений
n ' k i I s V 0 ,
П • k *4 V = 0 ,
п • а , • ( E - п 0 п ) | э v = 0 ,
п • а * • ( E - п 0 п )| д V = 0 ,
д6.
—- |д V =0 — в задаче (10)-(11);
д п
д6* .
—*- | д V = 0 — в сопряженной задаче. д п
Применение соотношений обобщенной биортогональности позволяет свести процедуру нахождения координатных функций ф i ( t ) к решению счетной последовательности несвязанных задач Коши для дифференциальных уравнений первого порядка с постоянными коэффициентами:
дФ i ( t ) д t
-^-фХ t )
< g > y * )
N , ’
ф (0) =
( ХеХ^уМНЫ )!^
N
( i = 0,1, _ , го ).
Решения полученных задач могут быть выражены через интеграл Дюгамеля:
t
Ф , ( t ) = v® х 0 - Н * [ у * ] + 5 , н 2 [ у * + X 0 , Н 2 [ у *» ] e 4 +J e ^ -"( gto , У * > d т ).
i 0
Если уравнения исходной задачи однородны, то есть массовые силы и источники тепла отсутствуют, а начальные скорости X 0 равны нулю, то формула для коэффициентов ф i ( t ) упрощается и принимает вид:
Ф , ( t ) = N (хо, Н * [ у * ] + ^ , н ; [ у - ] > e ’-' .
Далее соотношение (13) будет использоваться при построении решений модельных задач.
-
4. Спектральное уравнение
Необходимость применения численных методов при решении поставленной задачи напрямую зависит от того, возможно ли получить аналитические выражения для собственных значений и собственных функций ее дифференциального оператора. В случае тел канонических форм собственные функции могут быть получены в аналитической форме. Для этого следует использовать теорему Гельмгольца о разложении векторного поля на потенциальную и вихревую части [12]:
k = ∇φ+∇× ψ , ∇⋅ ψ =0.
Стандартная процедура разложения решения на продольную и поперечную волны [3, стр. 25] приводит к тому, что скалярный потенциал перемещений φ и температурная компонента θ собственной функции оператора могут быть выражены через решение скалярного уравнения Гельмгольца
ΔΦ+ζΦ=0
следующим образом: φ = p ∇Φ , θ = q Φ , где p и q — некоторые константы; условием существования нетривиального набора констант p и q служит равенство нулю следующего определителя:
( A + 1)( ζ+ξ 2 ) B
=0.
Dξζ -(ζ + Cξ)
Таким образом, возможность получения аналитических выражений для φ , θ обуславливается существованием явных формул для решений уравнения Гельмгольца в выбранной системе координат.
Потенциал ψ определяется из векторного уравнения Гельмгольца:
Δ ψ =( A + 1) ξ 2 ψ .
Для канонических областей его решение также может быть выражено через линейно независимые решения скалярного уравнения Гельмгольца [13, стр. 706], полученные методом разделения переменных:
ΔΨ- ( A + 1) ξ 2 Ψ =0.
Нахождение точных формул для собственных значений оператора H при произвольно выбранных граничных условиях невозможно. В следующем разделе настоящей статьи рассматриваются некоторые частные случаи, допускающие существование точных формул. Важную роль при этом играет уравнение (15), которое имеет смысл проанализировать.
Уравнение (15) можно рассматривать как квадратное уравнение относительно параметра ζ , либо как кубическое относительно ξ . Выражения для собственных функций yi , определенные через величины φ , ψ и θ , содержат произвольные постоянные cij и неизвестные пока собственные числа ξi оператора H . Поэтому при стандартном подходе дальнейшая процедура построения решения задачи заключается в нахождении произвольных постоянных. Выбор произвольных постоянных обуславливается граничными условиями, которым должны удовлетворять собственные функции. Условие существования нетривиального набора произвольных постоянных приводит к уравнению относительно ξ , к так называемому спектральному уравнению [10]. Это уравнение, в общем случае, является трансцендентным и имеет комплексные корни, для нахождения которых приходится применять численные методы. Следует отметить, что отделение корней спектрального уравнения представляет собой сложную вычислительную задачу, особенно для высокочастотной части решения.
С другой стороны, если для уравнения (14) поставить краевую задачу с граничными условиями, эквивалентными граничным условиям исходной задачи, то из решения этой вспомогательной задачи будет возможно найти значения параметра ζ . Тогда собственные значения ξ будут корнями кубического уравнения (15), переписанного следующим образом:
C ( A + 1) ξ 3 +ζ ( A + 1) ξ 2 +ζ [( C ( A + 1) + BD ] ξ+ζ 2( A + 1)=0. (16)
-
5. Случай точного определения собственных значений оператора
Рассмотренный способ построения решений начально-краевых задач при краевых условиях общего вида предполагает использование численных методов хотя бы для определения собственных значений порождаемых этими задачами дифференциальных операторов. При исследовании слабых эффектов, таких как связанность в задачах термоупругости для тел макроскопических размеров, погрешность, вносимая численными процедурами, может осложнить анализ получаемых результатов. Поэтому представляется важным выделить частные случаи краевых условий, при которых собственные значения оператора H определяются по точным формулам. Задачи с этими краевыми условиями могут использоваться в качестве модельных при реализации и отладке вычислительных алгоритмов рассматриваемого метода.
Пусть начальные условия задачи и внешние воздействия таковы, что часть решения, которая определяется вихревым потенциалом ψ , обращается в ноль. Тогда для компонент собственных функций yi становятся справедливыми равенства ki=pi∇Φi, θi=qiΦi.
Добавление к уравнению (14) граничного условия в форме Неймана приводит к вспомогательной задаче на собственные значения:
ΔΦ+ζΦ =0, n ⋅∇Φ | ∂ V =0.
Очевидно, что тогда имеет место следующее соотношение для трансляционных компонент k i собственных функций исходной задачи:
n⋅pi∇Φi|∂V=n⋅ki|∂V=0, а это означает отсутствие нормальных перемещений на границе тела: n⋅u|∂V=0.
Для температурных компонент собственных функций получается равенство
∂θ n ⋅qi∇Φi|∂V= |∂V=0,
∂ n
∂Θ из которого следует условие теплоизоляции границы: |∂V =0.
∂ n
Чтобы установить соответствие между граничным условием вспомогательной задачи (17) и условиями (12) задачи Штурма-Лиувилля, осталось выяснить, обращаются ли в нуль касательные напряжения на границе тела, когда n-УФ |dV = 0. Согласно закону Дюгамеля-Неймана о = Vu + (Vu) + [(A - 1)V-u - B0]E .
Отсутствие касательных напряжений на границе выражается равенством n - о - (E - n ® n) |дV = 0.
Это равенство будет справедливо, если n -У®УФ i - т | d V =0, где т — произвольный вектор касательной плоскости. Поскольку имеет место тождество т -V ( n -УФ i ) = т -V n -УФ i + n -У®УФ i - т , то с учетом условия n -УФ i | d V =0 можно записать: n -V ® УФ i - т | д V = - т - V n - УФ i | д V . Из последнего соотношения следует, что для обращения в нуль касательных напряжений достаточно, чтобы единичный вектор нормали не менял своего направления на границе тела:
V n | d v =0.
Таким образом, если для рассматриваемого тела выполняется условие (18), вместо решения задачи на собственные значения с краевыми условиями вида (12) можно решать вспомогательную задачу (17).
Условие (18) является справедливым, в частности, в случаях:
-
- для тела в форме прямоугольного параллелепипеда;
-
- для цилиндрических тел при условии осевой симметрии;
-
- для шарообразных тел при условии центральной симметрии.
-
6. Задача для конечного цилиндра
Во всех этих частных случаях решение вспомогательной задачи имеет простой вид. Далее приводятся решения задач для конечного цилиндра и шара.
Рассмотрим осесимметричную задачу связанной термоупругости для цилиндра с радиусом R и высотой H , на поверхности которого выполняются условия теплоизоляции, а также отсутствуют нормальные перемещения и касательная компонента вектора напряжений:
|
ur 1 r = R 0, |
u z 1 z =0 =0, |
u z 1 z = H 0 , |
|
∂Θ |
∂Θ |
∂Θ |
|
1 r = R = 0, ∂ r |
। z =0 = 0, ∂ z |
। z = H = 0 , ∂ z |
|
£ rz 1 r = R = 0, |
£ rz 1 z =0 = 0, |
£ rz 1 z = H = 0 . |
z
H
h
Рис. 1. Цилиндр с начальным распределением температуры
В начальный момент времени перемещения и скорости точек цилиндра равны нулю, а распределение температуры задается функцией Хевисайда n ( z ) (Рис. 1):
u 1 1 =0 =0, 1 1 =0 =0, ® 1 1 =0 = n ( z ) - П ( z - h ),
∂t где 0 < h < H .
В цилиндрической системе координат после перехода к безразмерным величинам вспомогательная краевая задача (17) при ζ ≠ 0 имеет решение
Φki(r,z)=J0(rζki-mk2)cosmkz, где mk = πkR/H, а параметр ζki есть i -й корень уравнения
J 1 ( ζ- m k 2 ) =0. (19)
Здесь J 0( r ) и J 1( r ) — функции Бесселя первого рода. Введем обозначение: s ki = ζ ki - m k 2 . Заметим, что корни ζ ki уравнения (19) действительны и неотрицательны, то есть имеет место неравенство ζ ki ≥ m k 2 .
Собственные функции дифференциального оператора H примут следующий вид ykiβ=(pkiβgradΦki,qkiβΦki), где β =1,2,3 обозначает номер корня уравнения (16) при фиксированном i . При ζ =0 решение вспомогательной задачи можно взять в виде Φ0 =1, а соответствующая собственная функция запишется: y0 = (0,0,0,1).
Поскольку сопряженная задача Штурма–Лиувилля отличается от исходной только коэффициентами, вспомогательная для нее задача совпадает с задачей (17), и ее решение при ζ ≠ 0 также может быть представлено в виде
Φnj(r,z)=J0(rsnj)cosmnz, где параметр ζnj , входящий в выражение для snj , есть j -й корень уравнения, получаемого из уравнения (19) заменой индекса k на n . Собственные функции оператора H* запишутся аналогично функциям ykiβ :
y * nj ν = ( p n * j ν grad Φ nj , q n * j Φ nj ) .
Здесь ν =1,2,3 обозначает номер корня уравнения (16) при фиксированном j . При ζ =0 имеет место равенство y * 0= y 0 .
Вычислим скалярное произведение, входящее в формулу (13) для коэффициентов разложения. При ζ ≠ 0 имеем
1 h 〈 x 0 , H 1* [ y * ki β ] + ξ ki β H *2 [ y * ki β ] 〉 =2 πζ ki BC ∫∫ Φ ki ( r , z ) rdrdz . 00
При любом фиксированном k первый корень уравнения (19) равен нулю, то есть sk 1 =0, тогда ζ k 1 = m k 2 , и с учетом равенства J 0 (0) = 1 получим
Φ k 1( r , z ) = Φ k 1( z ) =cos mk z .
Следовательно, в этом случае
h
-
< х 0 , нк w ] + Z k 1 p H [ У к 1 p ] ) = п m k BC J cos m k zdz = п m k BC sin( m k h ) . (20)
Заметим, что найденный результат не зависит от номера в корня уравнения (16).
Если же s ki > 0, что соответствует случаям, когда i >1, то выражение в левой части формулы (20) обратится в нуль:
-
*г *17' * * 2 nZ kiBC sin m k h
(x0, Hi [ykip ] + ^kipH2[ykiв I) J1 (ski) = 0 , mk ski поскольку ski является корнем уравнения (19).
Таким образом, для каждого фиксированного k в разложении все слагаемые будут равны нулю, кроме слагаемого, соответствующего i = 1. Поэтому при проведении дальнейших вычислений индекс i можно отбросить. Тогда, учитывая, что Z k = m k2 , уравнение (16) запишем в виде
C ( A + 1) Z 3 + m2k( A + 1) Z 2 + m k 2[( C ( A + 1) + BD ] Z + m k 4( A + 1) = 0 .
Отсюда при Z = 0 следует:
H
12 п R
<Х» H * ( y * ] > = - JJJ [ n ( z ) - n ( z - h ) ] Crdrd ф dz = -п Ch .
0 0 0
На рисунке 2 показано распределение собственных чисел оператора H на примере алюминиевого цилиндра с радиусом и высотой, равными 10 - 6 м. Числа, расположенные на действительной отрицательной полуоси, порождаются уравнением теплопроводности. Числа, расположенные вдоль мнимой оси, порождаются уравнением движения. Они слегка сдвинуты влево относительно мнимой оси, что обеспечивает затухание соответствующих форм колебаний. Видно, что при выбранных размерах цилиндра обе группы собственных значений имеют один и тот же порядок. В этом случае термоупругая волна максимально выражена. Следует отметить, что на характер распределения собственных значений влияет не только размер тела, но и свойства материала.
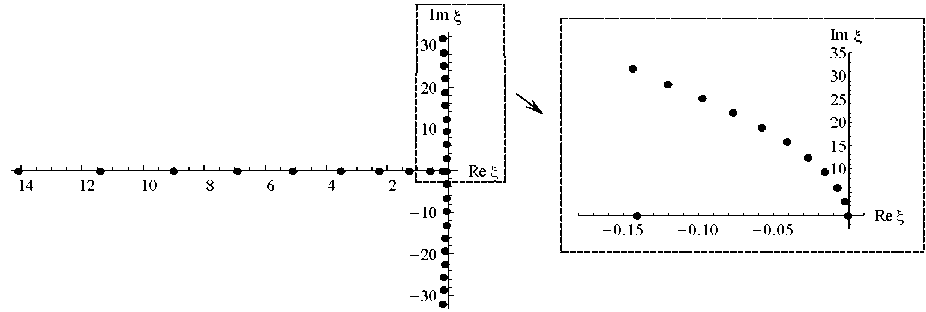
Рис. 2. Распределение собственных чисел на комплексной плоскости
Нормировочные коэффициенты N k в , соответствующие ненулевым слагаемым в разложении, определяются по формуле:
N k в = < Н 1 [ У k в ], У к P > + 2 Z k в < H 2 [ У k в ], У к в > .
После несложных преобразований будем иметь:
,, п Him 2
N k в = - "V 2 R
H
12 п R
[ BDm 4 + 2 ^ k в ( A + 1)( m 2 + C Z k в )2 ] для случая Z * 0,
N 0 = - JJ J rdrd ф dz = -
n CH
-----для случая Z = 0.
R
Собственные функции рассматриваемой пары взаимно-сопряженных операторов при k >0, n >0 запишутся в виде:
У k в = ( 0, 0, - m k ( m 2 + C Z k в )sin m k z, Dmk k в cos mkz ) , y n v = ( 0, 0, - m ( m 2 + C Z n v )sin mnz , - Bmn 2c°s m n z ) .
Подставляя найденные выражения в разложение, получим формулы для осевой компоненты вектора перемещений и температуры:
u = 2 RBC у Л ( m 2 + C Z k v ) sin m k h sin mk Z e ^ k v*
Uz H f ^lv L BDm^ 4 + 2 ^ k v ( A + 1)( m k + C Z k v ) 2 6 ,
^ = Rh 2 RBCD у у mk Z k v sin mkh cos mkz k v t
H " H H - L ^ =1 BDm k + 2 Z k V ( A + 1)( m k + C Z k v ) 2 e V .
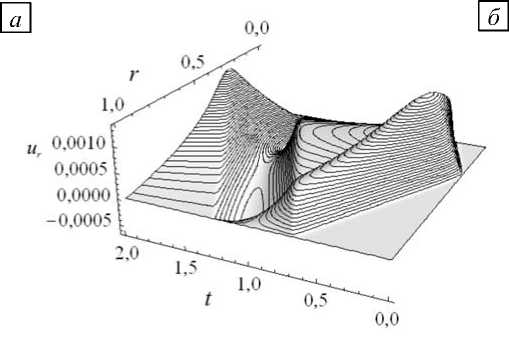
На рисунке 3 приведены зависимости от времени распределений относительной избыточной температуры 0 и осевого перемещения uz в безразмерных переменных для алюминиевого цилиндра с радиусом 10 - 6 м и такой же длиной при удержании 500 членов в разложении. На графиках хорошо видно, что с течением времени на фоне выравнивания температуры вдоль оси цилиндра происходит распространение прямой и отраженной волны тепловых возмущений. Амплитуда этих волн составляет несколько процентов от величины начального возмущения. Осевое перемещение тоже меняется волнообразно.
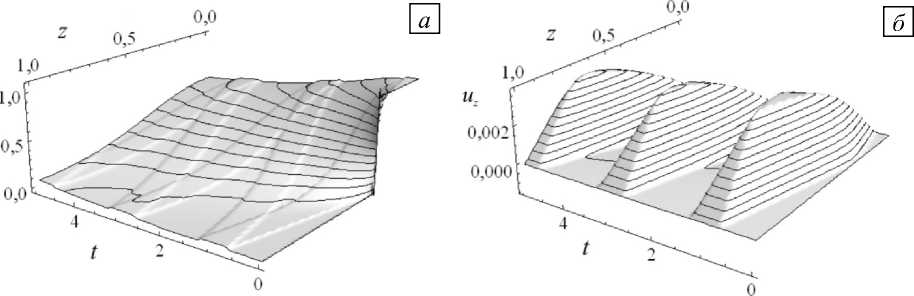
Рис. 3. Распределение во времени температуры 0 ( а ) и перемещения uz ( б) вдоль оси цилиндра
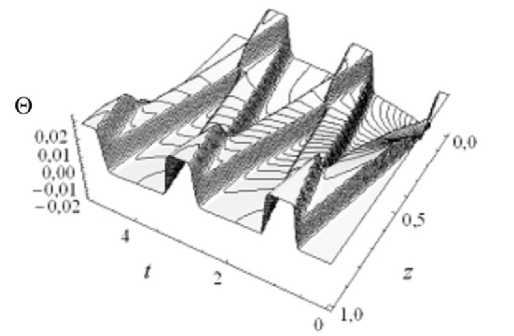
Рис. 4. Волновая составляющая температуры в задаче о цилиндре
На рисунке 4 показано распределение температуры, представляющей собой разность решений рассматриваемой задачи термоупругости и соответствующей ей задачи теплопроводности. Эта разность и есть та составляющая решения задачи термоупругости, которая возникает вследствие связанности температурного и механического полей.
-
7. Центральносимметричная задача для шара
Наряду с задачей связанной термоупругости для конечного цилиндра в качестве модельной рассмотрим центральносимметричную задачу для шара с радиусом R . Запишем граничные условия (12) для этой задачи:
u r | r = R =0,
∂Θ |
=0.
Начальные условия по-прежнему выбираем так, что начальные перемещения и скорости точек шара равны нулю, а начальное распределение температуры определяется функцией Хэвисайда:
u | t =0 =0, ∂ u | t =0 =0, Θ | t =0 = η ( r ) -η ( r - h ),
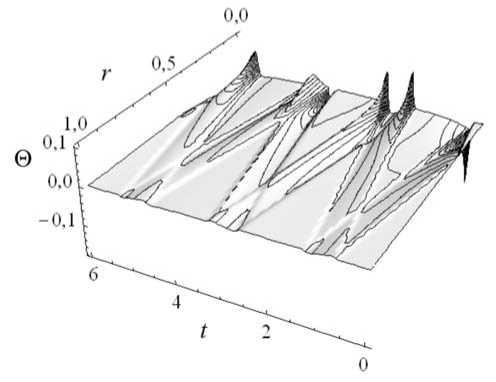
∂t где 0< h Вспомогательную краевую задачу вида (17) рассмотрим в сферической системе координат также при условии центральной симметрии. В безразмерном виде при ζ ≠ 0 ее решение выразится следующим образом: Φ = sin( d. ζir) ir где ζi — i -й корень уравнения ζcos ζ-sin ζ= 0 . При ζ =0 решение вспомогательной задачи возьмем в виде Φ0 =1, тогда соответствующая собственная функция запишется как y0 = (0, 0, 0,1) . Выполнив вычисления, аналогичные проделанным в задаче для цилиндра, при ζ ≠ 0 имеем: 〈x0,H1*[y*ij]+ξijH*2[y*ij]〉=4πBC(sinζih-ζihcosζih). Как и в случае с цилиндром, значение этого скалярного произведения не зависит от номера J корня уравнения (16). При Z = 0 получим: 1 п2п д 3 (x0,H*[y0]>= -JJj [n(z)-n(z-h)]Cr2 sin6drd9dФ = —^— • 000 3 Нормирующий множитель при Z ^ 0 вычисляется из соотношения: N, = -4л[ BDZ 3 + 2Z,,(A + 1)Zi(Zi + CZ ,)2 ] 2 ^4 ^ ^' а при Z = 0 имеет место равенство 1П2П N = -ДJ Cr2 sin 9drd9dФ = —• 000 3 Собственные функции дифференциального оператора при i >0 запишутся в следующем виде: yij (Zi + CZj) x Z r cos а/Z r - sin a Z r V ~ i________V ” i__________V ~ i 0, 0, DzyZi sin V Zr В результате получим формулы для перемещения и температуры: ur 4BC r2 ^ 3 zz i=1 j=1 VZ■ (Zi + CZ,- Vsin VZ r - VZ r cos VZ r) (sin VZh iiij iiii - VZ h cos V ~ l 7 ih) (2 4Zi - sin 2 VZi)[ BDZ 3 + 2Z,Z.( A +1) (Zi + CZ, )2 Z-1 eZlJ 0 = h = - 4BCD zz r =1 j=1 ZnZi-JZ■ sin VZ r (sin VZh - VZh cos VZ h) j e (2 VZi - sin 2 VZi)[BDZ3 + 2ZjZi( A + 1)(Zi + CZ, )2] Найденное решение является ограниченным при r ^ 0. Чтобы убедиться в этом, достаточно посмотреть на формулу для избыточной температуры 0 : в ней имеет место первый замечательный предел, а значение компоненты перемещения ur стремится к нулю при r ^ 0, поскольку sin АIZ r - zZ r cos лIZ r lim 2 =0. r ^0 r На рисунке 5 приведены зависимости от времени распределений относительной избыточной температуры 0 и радиального перемещения ur в безразмерных переменных для алюминиевого шара с радиусом 10-6 м при числе слагаемых в разложении, равном 500. Из графиков видно, что температурные волны довольно быстро затухают при распространении от центра шара к его границе. При этом вблизи центра амплитуда температурных волн сравнима с амплитудой волн в рассмотренном ранее цилиндре. Таким образом, можно предположить, что на скорость затухания термоупругих возмущений влияет форма тела. Рис. 5. Распределение во времени температуры Θ (а) и перемещения ur (б) вдоль радиуса шара Рис. 6. Волновая составляющая температуры в задаче для шара На рисунке 6 показано распределение температуры, представляющей собой, как и в задаче для цилиндра, разность решений рассматриваемой задачи термоупругости и соответствующей ей задачи теплопроводности. Построенные замкнутые решения задач термоупругости для конечного цилиндра и шара при некоторых частных случаях краевых условий позволили определить, как меняется амплитуда термоупругих волн в зависимости от характерного размера тела. Проведенный анализ подтверждает исходное предположение авторов о том, что влияние связанности термомеханических полей усиливается по мере уменьшения размеров рассматриваемого тела, что выражается в увеличении амплитуды термоупругих волн по отношению к высоте начального теплового импульса. В результате численных экспериментов установлено: – термоупругая волна становится все более выраженной по мере уменьшения размеров тела вплоть до величины порядка 10-6 м; при таких размерах амплитуда температурных волн в металлах составляет 2–5% от высоты начального теплового импульса; дальнейшее уменьшение размеров тела приводит к уменьшению амплитуды волн; – в проявлении эффекта связанности определяющей является не соразмерность коэффициентов уравнений движения и теплопроводности, а плотность распределения собственных значений порождаемого задачей дифференциального оператора; – в телах микронного масштаба температурные волны имеют достаточную амплитуду, чтобы их можно было фиксировать современной аппаратурой; детектируемые термоупругие волны могут служить источником информации о наличии микровключений в поверхностных слоях различных конструкций [14]. Полученные результаты могут использоваться в качестве основы для разработки математических моделей новых методов неразрушающего контроля. Работа выполнена при финансовой поддержке РФФИ (проекты № 08-01-00553-a, 09-08-01194-a, 09-01-00343-a, 09-08-01180-a). 1. Снеддон И.Н., Берри Д.С. Классическая теория упругости. – М.: ГИ Физ.-мат. лит., 1961. – 220 с. 2. Сеницкий Ю.Э. К решению связанной динамической задачи термоупругости для бесконечного цилиндра и сферы // Прикл. механика. – 1982. – Т. 18, № 6. – С. 34-41. 3. Новацкий В. Динамические задачи термоупругости. – М.: Мир, 1970. – 256 с. 4. Новацкий В. Теория упругости. – М.: Мир, 1975. – 872 с. 5. Лычев С.А., Сеницкий Ю.Э. Несимметричные интегральные преобразования и их приложения к задачам вязкоупругости // Вестник Самарского гос. ун-та. Естественнонаучная серия. Спец. выпуск. – 2002. – С. 16-38. 6. Лычев С.А. Связанная динамическая задача термовязкоупругости // Изв. РАН. МТТ. – 2008. – № 5. – С. 95-113. 7. Таблицы физических величин / Под ред. И.К. Кикоина. – М.: Атомиздат, 1976. – 1008 с. 8. Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов в гильбертовом пространстве. – М.: Наука, 1965. – 448 с. 9. Келдыш М.В. О полноте собственных функций некоторых классов несамосопряженных линейных операторов // УМН. – 1971. – Т. 26, Вып. 4(160). – С. 15-41. 10. Маркус А.С. Введение в спектральную теорию полиномиальных операторных пучков. – Кишинев: Штиинца, 1986. – 260 с. 11. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1971. – 589 с. 12. Морс Ф.М., Фешбах Г. Методы теоретической физики. – М.: ИЛ, 1958. – Т. 1. – 931 с. 13. Морс Ф.М., Фешбах Г. Методы теоретической физики. – М.: ИЛ, 1960. – Т. 2. – 897 с. 14. Cernuschi F., Figari А., Fabbri L. Thermal wave interferometry for measuring the thermal diffusivity of thin slabs // J. of Mat. Sci. – 2000. – V. 35, N 23. – P. 5891-5897.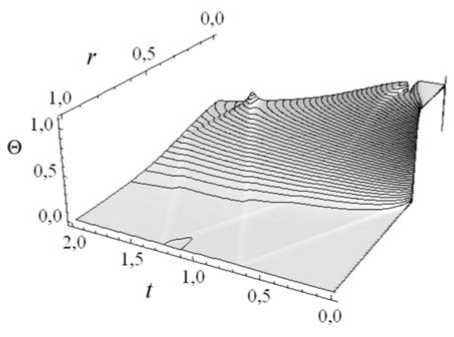
8. Заключение
Список литературы Замкнутые решения динамических задач связанной термоупругости для цилиндра и шара
- Снеддон И.Н., Берри Д.С. Классическая теория упругости. -М.: ГИ Физ.-мат. лит., 1961. -220 с.
- Сеницкий Ю.Э. К решению связанной динамической задачи термоупругости для бесконечного цилиндра и сферы//Прикл. механика. -1982. -Т. 18, № 6. -С. 34-41.
- Новацкий В. Динамические задачи термоупругости. -М.: Мир, 1970. -256 с.
- Новацкий В. Теория упругости. -М.: Мир, 1975. -872 с.
- Лычев С.А., Сеницкий Ю.Э. Несимметричные интегральные преобразования и их приложения к задачам вязкоупругости//Вестник Самарского гос. ун-та. Естественнонаучная серия. Спец. выпуск. -2002. -С. 16-38. 6.
- Лычев С.А. Связанная динамическая задача термовязкоупругости//Изв. РАН. МТТ. -2008. -№ 5. -С. 95-113.
- Таблицы физических величин/Под ред. И.К. Кикоина. -М.: Атомиздат, 1976. -1008 с.
- Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов в гильбертовом пространстве. -М.: Наука, 1965. -448 с.
- Келдыш М.В. О полноте собственных функций некоторых классов несамосопряженных линейных операторов//УМН. -1971. -Т. 26, Вып. 4(160). -С. 15-41.
- Маркус А.С. Введение в спектральную теорию полиномиальных операторных пучков. -Кишинев: Штиинца, 1986. -260 с.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. -М.: Наука, 1971. -589 с.
- Морс Ф.М., Фешбах Г. Методы теоретической физики. -М.: ИЛ, 1958. -Т. 1. -931 с.
- Морс Ф.М., Фешбах Г. Методы теоретической физики. -М.: ИЛ, 1960. -Т. 2. -897 с.
- Cernuschi F., Figari А., Fabbri L. Thermal wave interferometry for measuring the thermal diffusivity of thin slabs//J. of Mat. Sci. -2000. -V. 35, N 23. -P. 5891-5897.


