Зарядка и подвижность субмикронных и наночастиц в катодной области тлеющего разряда

При зарядке частиц размером свыше 2-3 мкм в прикатодной области тлеющего разряда за счет направленного движения ионов справедлива формула Потенье [6]. Если частица имеет форму шара, то неравномерное распределение заряда на поверхности приводит к беспорядочному вращению частицы из-за опрокидывающего действия электростатических сил. Благодаря этому избыточный заряд распределяется по поверхности частицы равномерно. В этом случае заряд крупных частиц равен:

q ( t ) = 12 ns ₀ Ea ²(1 + 2

s -1) jt s + 2 4s0 E + jt

где ε — относительная диэлектрическая проницаемость материала частицы, j – плотности тока и E напряженность поля в катодной области.

Это выражение определяет кинетику зарядки сферической диэлектрической частицы радиусом a в поле разряда со средней напряженностью Е . При этом можно пренебречь диффузией ионов к частице. В проведенных экспериментах плотность тока при НЧ разряде (частота 10³ Гц) в тетрафторэтилене j =1,2 А/м², а средняя напряженность в катодной области – около 60 кВ/м. Для других исследованных веществ, таких как стирол, гексаметилдисилазан и октаметилтрисилоксан, зависимость заряда от времени имеет тот же характер. Следует отметить, что частота разрядного тока (1кГц) такая, что разряд успевает за период действующего напряжения дважды зажечься, и каждый из электродов за период становится катодом и анодом. Поэтому в таких условиях важна кинетика нарастания заряда на частице, поскольку в этом случае важно знать, какие частицы успевают долететь до поверхности электрода за половину периода напряжения, а какие нет.

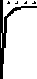
0 -----------------------1------------------------1------------------------1------------------------1------------------------

0      0.1     0.2     0.3     0.4     0.5

t, ms

Рис. 1. Кинетика «ударной» зарядки частиц сферической формы радиусом 1 μm – 1, радиусом 0,5 μm – 2. По горизонтальной оси – время, по вертикальной оси – число элементарных зарядов

Анализ кинетики зарядки (рис. 1) показывает, что 90% от максимального заряда частица приобретает за время около 0,01 мс. Учитывая, что период напряжения разрядного тока 1мс, при дальнейших расчетах можно пренебречь зависимостью заряда от времени для ударной зарядки и считать заряд частицы максимально возможным. Если частицы достаточно малы, то движение ионов к частице происходит в основном под действием градиента их концентрации. Для сферических частиц плотность потока ионов равна:

f = Kn —-—- r - D • grad (n) 4ne0 r3 .

Вследствие сферической симметрии распределения плотности потока ионов и, используя известное соотношение между коэффициентом диффузии и подвижностью

K _ e_

D ~ kT

, можно записать дифференциальное уравнение для диффузионной зарядки dq dt

j • q

Е е о exp V

e q

V kT 4 ле ₀ a )

^^^^^^^^

где k – постоянная Больцмана. Последнее выражение получено, исходя из предположения, что в непосредственной близости от поверхности частицы концентрация ионов равна нулю. В качестве граничного условия мы предположили, что в начальный момент времени заряд частицы равен максимальному заряду, рассчитанному по формулам ударной зарядки. Решение этого уравнения было выполнено численно с использованием программы Mathcad.

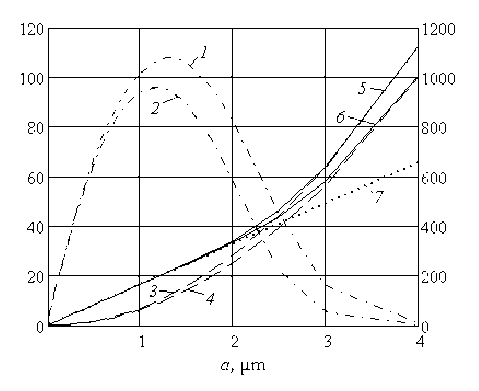
Рис. 2. Зависимости заряда сферических частиц, приобретаемого за время 0,5 ms, от радиуса а. По вертикальным осям – число элементарных зарядов. Кривые 1, 2 – левая ось, 3-7, правая

Основные результаты этих расчетов сводятся к следующему: практически во всем диапазоне напряженностей, встречающихся в реальных условиях, формула Потенье (1) справедлива для частиц размером более 3-4 мкм, а диффузионная зарядка достигает максимальных значений для частиц размером около 1-1,5 мкм. Это можно увидеть на рис. 2, где представлены: 1 и 2 – кривые «диффузионной» зарядки для тетрафторэтилена и стирола соответственно, 3 и 4 – кривые «ударной» зарядки для стирола и тетрафторэ-тилена соответственно, 5 и 6 –заряд частиц с учетом «ударного» и «диффузионного» механизмов зарядки. Хорошо видно, что кривые 5 и 6 полностью совпадают для частиц, радиусы которых меньше 1,5 мкм. Здесь основную роль играет процесс диффузионной зарядки, и, следовательно, отсутствует влияние таких параметров, как диэлектрическая проницаемость и молярная масса полимеризующегося вещества, поэтому заряды на частицах разных веществ одинакового размера оказываются равными. Однако на этом участке сильно проявляется зависимость заряда частиц от напряженности внешнего поля и плотности тока. Исходя из вышеизложенного, для этого участка нами получена апроксимационная формула

Z (t, a) = | 20,33 • ln[ j • t | + 538 I-a, I IE ) J где а – радиус частицы (выражен в мкм), Z(t, a) – количество положительных элементарных зарядов. Данная формула хорошо описывает зависимость заряда от размера частицы и может быть использована для широкого диапазона плотностей электрического тока и не слишком сильных полей (напряженностью менее 100 кВ/м). На рис. 2 расчету заряда по апроксимационной формуле соответствует прямая 7.

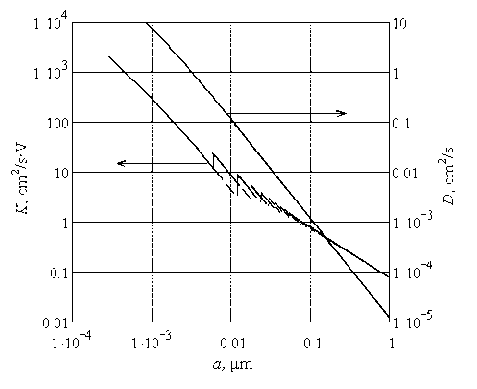
Рис. 3. Зависимость подвижности К и коэффициента диффузии D от радиуса частицы а

Подвижность ионов согласно строгой теории Ланжевена [7] записывается в следующем виде:

K =

0,75eM

2 ,J1 + d 12Aj^nPp

где ρ – плотность газообразного мономера, М – масса молекулы мономера, m – масса заряженной частицы, р — давление газообразного мономера, а d 12 — сумма радиуса частицы и радиуса молекулы. И тогда коэффициент взаимной диффузии для наночастиц и молекул газа равен

D 12 =

3 n kT   1

ФM r n_o n d 122

где М r – приведенная масса молекулы и частицы, n 0 – концентрация газа, Т – температура. Графики зависимости подвижности и коэффициента взаимной диффузии от размера частицы при температуре 300 К и давлении 80 Па приведены на рис. 3 (масштаб по осям логарифмический). Ломаный вид кривой подвижности связан с зависимостью от заряда частиц: поскольку количество элементарных зарядов не может быть дробным, необходимо было округлять их до целых значений. Частицы радиусом меньше 0,05 мкм несут меньше 10 элементарных зарядов, при этом разница в один заряд существенно влияет на подвижность. Непрерывная кривая подвижности на рис. 3 соответствует округлению количества зарядов в большую сторону, кривая крупным пунктиром – округлению в меньшую сторону.

Выводы: наночастицы различных размеров, возникающие в катодной области разряда, заряжаются и начинают двигаться под действием электрического поля. В результате возникает распределение частиц по скоростям их направленного движения к катоду. Это неизбежно приводит к механизму динамической коагуляции частиц различных размеров, поскольку скорости мелких частиц существенно выше, чем крупных. Подобный механизм отмечался в работе [5] при формировании газодинамических потоков из области разряда на периферию реактора, однако он был связан с имеющимся в этой области градиентом температуры. В данном случае динамический режим коагуляции связан с движением и зарядкой в электрическом поле дисперсных частиц. При движении заряженных частиц к катоду происходит эволюция их размеров, в результате формирование покрытия на поверхности катода будет осуществляться из разноразмерных нанодисперсных частиц, свидетельством чему является поверхностная макроструктура полимерных пленок [3, 5]. Кроме того, чаще всего, именно в катодной области отмечается образование вихреобразных облаков из наночастиц [3, 5, 8].

Рассмотренные выше механизмы касаются процессов переноса – транспорта в электрическом поле катодной области как химически активных частиц – ионов, так и наночастиц, образующихся в разряде и оказывающих влияние на формирование полимера и его свойства [3, 5]. Последнее направление является наименее изученным, поэтому исследования процессов переноса в разряде, кроме практического значения, представляет собой самостоятельную научную ценность.