Затупленное осесимметричное тело минимального сопротивления в гиперзвуковом потоке разреженного газа

Построение тела, оптимального по одной из интегральных характеристик движения (сопротивлению или теплоотдаче), является актуальной проблемой механики. Интерес к этой области науки обусловлен нуждами авиационно-космической промышленности и связан с необходимостью совершенствования ракетной и авиационной техники.

Решения задач оптимизации формы тела, по интегральным характеристикам движения возможны лишь при наличии соотношений, явно связывающих силы, действующие на. поверхности контакта, среды и тела, с формой его поверхности. Параметры среды при обтекании тела находятся из решения краевой задачи для системы дифференциальных уравнений в частных производных. Задача, оптимизации формы тела, в такой постановке, базирующейся на точных уравнениях такого рода, для большинства сред практически не разрешима. В этих случаях естественно искать упрощения, позволяющие найти приближенное решение. В первую очередь они делаются для сил, действующих на. поверхности тела, для которых используются формулы, полученные из приближенных моделей.

Для оценочных расчетов сил, действующих на. тело при его высокоскоростном движении в газе, широкое распространение получили формулы, найденные из локальных моделей. В основе этих моделей лежит предположение, что каждый элемент поверхности

тела взаимодействует со средой независимо от других участков тела и сила, действующая на него, зависит лишь от ориентации элемента относительно направления движения. Эта зависимость может включать в себя скорость движения и характеристики среды, которые считаются постоянными. Примером такой зависимости является формула Ньютона, используемая в гиперзвуковой аэродинамике для оценочных расчетов распределения давления на поверхности тела или зависимости, полученные из модели свободномолекулярного движения для сильно разреженных газов. Использование таких формул позволяет записать силы, действующие на тело, в виде интегралов по поверхности, и методами вариационного исчисления они могут быть исследованы на экстремум.

Классическая задача построения тела вращения минимального сопротивления с использованием формулы Ньютона решалась во многих работах [1-6]. Были заработаны эффективные численные методы решения таких задач [7]. В связи с развитием космической техники появился интерес к оптимальным задачам высокоскоростной аэродинамики на больших высотах в разреженном газе [8-10].

Дальнейшее упрощение таких задач связано с использованием целевых функций разного вида зависящих от некоторого количества параметров, по которым и производится оптимизация [11-13]. В частности, широкое распространение получила степенная целевая функция [14, 15]. В данной работе использование целевой степенной функции вместе с локальными методами [15-18] (формулы свободномолекулярной аэродинамики, формула Ньютона, формулы локального метода гиперзвуковой аэродинамики) позволило свести вариационную задачу минимизации функционала (сопротивление тела вращения) к задаче поиска экстремума функции от одной или двух переменных. Решаются задачи об определении формы затупленных тел вращения в гиперзвуковом потоке разреженного газа в широком диапазоне чисел Рейнольдса.

2.    Форма тела вращения минимального сопротивления большого удлинения

Задано тело вращения длиной L и радиусом основания R. Требуется определить форму образующей х (г) такую, при которой это тело имеет минимальное сопротивления в гиперзвуковом потоке газа. Скорость газа V^ направлена вдоль оси вращения Ох. Ө - угол между внутренней нормалью п и вектором скорости.

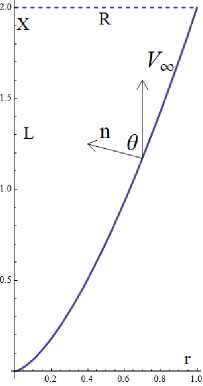
Рис. 1. Схема, обтекания тела, вращения

Ср и Ст - нормальная и касательная аэродинамические силы, действующие на элемент поверхности ds, отнесенные к скоростному напору pV^/2 (р - плотность газа) и площади этого элемента. Тогда коэффициент сопротивления Ст (аэродинамическая сила, действу ющая на тело вдоль вектора скорости, отнесенная к скоростному напору и характерной площади, в данном случае — это площадь основания, то есть тВ?) будет равен

Сx =

Здесь

2 ^R

B2L (Ср

• cos Ө + Ст • sin Ө)

г

dr.

cos Ө =

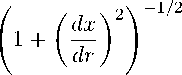
Рассмотрим два случая применения локальных методов: формула Ньютона и свободномо-

.пекулярное приближение. В случае формулы Ньютона

Ср = 2 cos² Ө,   Ст = 0.

Уравнение (1) запишется следующим образом (линейные размеры отнесены к В): ^Сзс = ⁴ / 1 + (dx/dr)^{2 dr.}

Будем рассматривать случай большого удлинения, то есть dx/dr ~ L/В = А >>  1. В интеграле (3) пренебрегаем единицей по сравнению с квадратом производной. Если подынтегральную функцию обозначить F (r, dx/dr), то уравнение Эйлера [4] будет иметь вид d^ F (r,u) = С, u = dx/dr, и при x (0) = 0, x (В) = L решение будет иметь вид

r \ ^{4/3 x}= ^LU

.

Или в безразмерном виде x = А • r^4/3. Коэффициент сопротивления равен 27

^С(С = 16А².

В свободномолекулярном высокоскоростном приближении [16, 17] Ср = 2 cos² Ө + z cos Ө, z = лУirt_w (7 — 1) /7 , Ст = 2 cos Ө sin Ө.

Здесь tw = Tw/То - температурный фактор, Тш - температура поверхности тела, То - температура торможения, 7 - показатель адиабаты. Уравнение (1) запишется в виде

Сx = 2 + 2z [

aJ 1 + (dx/dr)²

При больших удлинениях, используя уравнение Эйлера, получаем x = А • r³ / ².

Коэффициент сопротивления равен

^Gx = ^{2 +} 8А'

Свободномолекулярное приближение и приближение Ньютона в некотором смысле можно считать предельными случаями разреженности газа: свободномолекулярное приближение -это сильно разреженный газ, а приближение Ньютона - это сплошная среда. Отметим, что форма тела вращения минимального сопротивления при большом удлинении представляет собой степенную функцию, причем величина степени зависит от разреженности газа.

3.    Тела вращения произвольного удлинения

Как уже отмечалось, форма тела вращения минимального сопротивления при большом удлинении представляет собой степенную функцию, причем величина степени зависит от разреженности газа. Естественно для произвольных удлинений в качестве целевой выбрать степенную функцию x = L (r/В)9 . (10)

В этом случае задачу можно сформулировать так: найти величину 3. такую, чтобы коэффициент сопротивления был минимален при заданной величины А. В случае модели Ньютона уравнение для величины коэффициента сопротивления запишется в виде гипер- геометрической функции Ғ[а, Ь, с, d\

Сх = 4 /

------ -----2dr = 2Ғ fl, —,-Д-, —P ²A²) .            (11) 1 + (AP-^^-1)              ^{P — 1 P — 1}

Таким образом, задача вариационного исчисления свелась к поиску минимума функции одной переменной. В табл. 1 представлены величины P и Сх в зависимости от удлинения A. Заметим, что во многих работах ось вращения — это ось Ох. В этом случае величина показателя степени в степенной функции а = P^-1. В табл. 1 также представлена величина а.

Таблица!

A	1	3	5	7	9	10	15	20
P	2.16	1.42	1.362	1.35	1.344	1.342	1.337	1.336
а	0.463	0.704	0.734	0.741	0.744	0.745	0.749	0.749
Сх	0.803	0.17	0.064	0.034	0.018	0.017	0.0075	0.0042

На рис. 2. изображена зависимость а = P ^-1 от удлинения A. При больших удлинениях эта зависимость стремится к а = 3/4 = 0.75, как получено в п. 1 для случая больших удлинений.

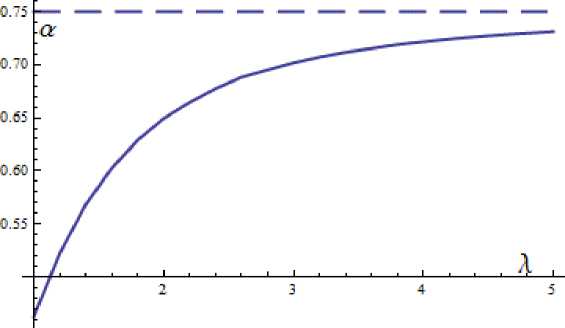
Рис. 2. Зависимость а = P ¹ от величины удлинения A

В случае свободномолекулярной модели, используя (7) и (10), коэффициент сопротив ления выражается уравнением

^Сх = ² + 2z I                  ^d- = ^Ғ f-, - -,- -, ^—P 2^A2^ .         (12)

^J0 ^1 ₊ (AP-/3-1)²        V - ^{— 1 P — 1}       /

В табл. 2 представлены величины P,а и Сх в зависимости от удлинения A.

Т а б л и ц а 2

A	1	3	5	7	9	10	15	20
P	2.868	1.681	1.571	1.539	1.525	1.52	1.51	1.506
а	0.349	0.595	0.636	0.65	0.656	0.658	0.662	0.664
Сх	2.182	2.083	2.052	2.038	2.029	2.084	2.018	2.013

На рис. 3. изображена зависимость а = P ^-1 от удлинения A. При больших удлинениях эта зависимость стремится к а = 2/3 = 0.667, как получено в п. 1 для больших удлинений в свободномолекулярном случае.

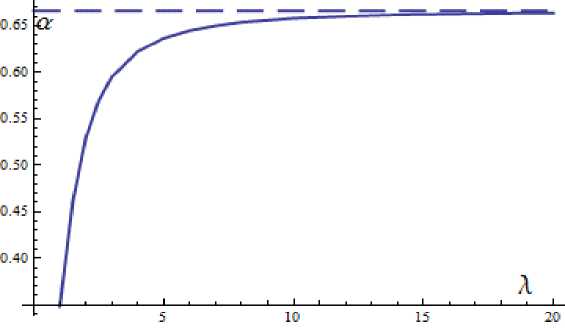
Рис. 3. Зависимость a = /3 ¹ от величиньi удлинения A, t_w = 0.1, 7 = 1.4

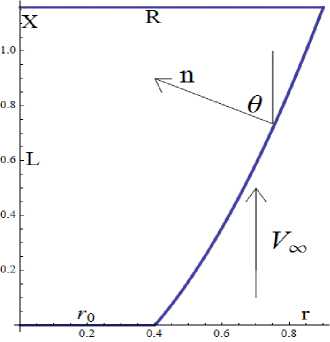
Рис. 4. Схема, обтекания тела, с плоским торцом

4. Затупленные тела вращения большого удлинения

Известно [1], что тела вращения с плоским торцом имеют меньшее сопротивление, чем тела без затупления. Задано тело вращения длиной L, радиусом основания R и плоским торцом с радиусом го. Требуется определить форму образующей х (г) и величину го, такие, при которых это тело имеет минимальное сопротивление в гиперзвуковом потоке газа.

В случае формулы Ньютона для торца Ср = 2, а для образующей Ср = 2 cos² Ө. Уравнение для величины коэффициента, сопротивления запишется в виде

сх =2(^+ r $:

г

1 + (dх/dг')‘²

dr.

Пренебрегая в (13) единицей по сравнению с квадратом производной из уравнения Эйлера, получаем так же, как в п. 1

х (г) = <

0, ид-д/3

^L R4^3-r 4^/3 ’

0 < г < г_о, г_о < г < R.

Уравнение для коэффициента, сопротивления A = L/RY

имеет вид (величина го отнесена к R,

^Сх = ^2Т'о ⁺ 1^ ⁽¹ - ^г 4 ^{/ 3 ) 3} ‘

При больших A величины го, при которых достигается минимум Сх, представлены в табл. 3. Там же дано сравнение значений Сх для тел с затуплением и значений Схо без затупления.

Величины го зависят от значений удлинения A. Для больших удлинений можно приближенно записать эту зависимость в виде го = 2.19/A3. На рис. 5 показана эта зависимость.

Т а б л и ц а 3

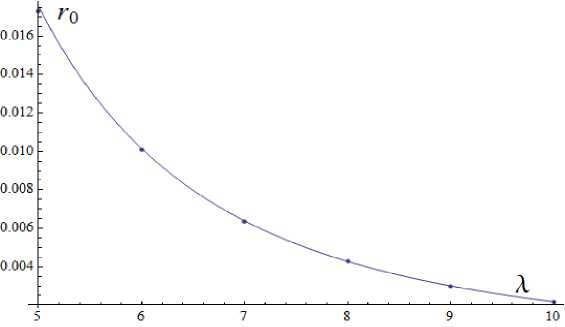
Рис. 5. Зависимость то от удлинения А в случае модели Ньютона. Точки - точные значения, линия -приближеииая зависимость

А	5	6	7	8	9	10
то	0.0173	0.0101	0.00637	0.00427	0.003	0.00219
Сх	0.0672	0.04677	0.0344	0.02635	0.02082	0.01687
Схо	0.0675	0.04687	0.03444	0.02637	0.02083	0.016875

Несмотря на то, что величина радиуса затупления мала, значение коэффициента сопротивления затупленного тела вращения меньше, чем в случае отсутствия затупления (хотя разница очень небольшая).

Аналогично рассмотрим свободномолекулярную модель газа. Используя уравнения (1),

(6), (7), получим

^{Сх 2 +2} ( R ) ⁺ № /₀ vn^ "^{т                (16)}

Вычисляя минимум интеграла в уравнении (16), так же, как в п. 1 получаем х (т) = <

0,

^

^L В^-^ / ’

0 < т < т_о, т_о < т < R.

Уравнение для коэффициента сопротивления

имеет вид (величина то отнесена к R,

А = L/R\.

^Сх = ^{2; 2т}2 + 8А ⁽1 — Д ^{2 )2}.                          (18)

При больших А величины то, при которых достигается минимум Сх в свободномолекуляр

ном случае, представлены в табл. 4, t_w = 0.1, 7 = 1.4. Там же дано сравнение значений Сх для тел с затуплением и значений Схо без затупления.

Т а б л и ц а 4

А	5	6	7	8	9	10
то	0.069	0.048	0.0358	0.0275	0.021	0.017
Сх	2.052	2.044	2.037	2.032	2.0295	2.026
Схо	2.053	2.0443	2.038	2.033	2.0296	2.0267

Так же, как и в случае модели Ньютона, наличие затупления уменьшает величину коэффициента сопротивления. Величины то зависят от значений удлинения А. Для больших удлинений можно приближенно записать эту зависимость в виде то = 0.0011 + 1.687/А2. На рис. 6 показана эта зависимость.

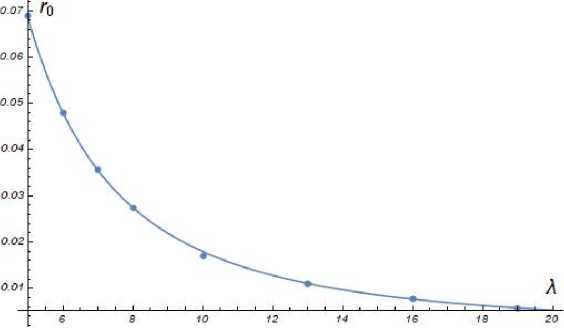
Рис. 6. Зависимость то от удлинения А в свободномолекулярном случае, t_w = 0.1, 7 =1.4. Точки -точные значения, линия - приближенная зависимость

5.    Затупленные тела вращения произвольного удлинения Для модели Ньютона запишем уравнение (13) в виде Сх = 2т2 +4 0q —— 1+ 1 т ^т т@^1 -40 Д2dT - 4ТО Jo1   , 1+ АУЫ т . 5-1 1-4 т^-1 ) -2 dт = — 2г 2         — Д = 2т 0 + 2Г 1’ Д-1 ’ Д-1 ’ - 1’ Д-1’ Д-1’ -

Здесь F (a,b,c,d) - гипергеометрическая функция. Таким образом, вариационная задача свелась к поиску минимума функции (19) по двум переменным 3 и то при заданном удлинении А.

В табл. 5 представлены разультаты расчетов величин 3, a = 3 ^-1 и то в зависимости от удлинения А, при которых достигается минимум Сх и, для сравнения, величины Схо при тех же удлинениях, но без затупления (то = 0).

Т а б л и ц а 5

А	3	a	то	Сх	Схо
1	1.571	0.636	0.352	0.75	0.803
2	1.448	0.691	0.123	0.321	0.33
3	1.399	0.715	0.0498	0.165	0.167
4	1.375	0.727	0.0293	0.0982	0.0986
5	1.362	0.734	0.0131	0.0645	0.0646
6	1.355	0.738	0.00786	0.0454	0.0455
7	1.349	0.741	0.00507	0.0336	0.0337
8	1.346	0.743	0.00346	0.0259	0.0259
9	1.344	0.744	0.00246	0.0205	0.0205
10	1.342	0.745	0.00181	0.0167	0.0167
15	1.337	0.748	0.00055	0.00746	0.00746
20	1.335	0.749	0.00023	0.00421	0.00421

При малых удлинениях величина радиуса затупления велика, а коэффициент сопротивления существенно меньше, чем без затупления. Начиная с А = 8, несмотря на затупление, коэффициент сопротивления становится практически одинаковым в обоих случаях.

6.    Затупленные тела вращения — локальный метод для гиперзвуковых течений

Для оценочных расчетов сил, действующих на тело при его высокоскоростном движении в газе, распространение получили формулы, найденные из локальных моделей. В основе этих моделей лежит предположение, что каждый элемент поверхности тела взаимодействует со средой независимо от других участков тела и сила, действующая на него, зависит лишь от ориентации элемента относительно направления движения. Эта зависимость включает в себя скорость движения и характеристики среды. Наибольшего распространения получила локальная модель из [17-18], в которой коэффициенты давления и трения равны

Ср = р₀ cos ² Ө + р_і cos Ө, Ст = т₀ cos Ө sin Ө.                    (20)

Функции ро, pi, то зависят от числа Reo, температурного фактора tw и показателя степени адиабаты у:

р о = 2, p i = г exp [— (0.125 + 0.078t_w) Re o ] , г = ^ ту/ , = _____________ 5 . 23_____________ _e = _Rp Щ 3 _t„ ₊ 1 \- 2 / 3

• ⁰      [ s +6 . 88 exp(0 . 0072 s- 0 . 000016 s² )] ¹ / ² ’             ^{014 W} 4'      ^.

Здесь tw = Tw/То - температурный фактор, Tw - температура поверхности тела, То - температур а торможения То = Т^ (1 + S2 (у — 1) /у), у - показатель адиабаты, Re0 = p^V^R/p (То), рЮ’ ҮЮ’ Т^ - плотность, скорость и температура невозмущенно го потока газа, p (То) - коэффициент вязкости в зависимости от температуры торможения.

Задано тело вращения длиной L и радиусом основания R. Требуется определить форму образующей х (т), такую, при которой это тело имеет минимальное сопротивления в гиперзвуковом потоке газа. Скорость газа 1Д направлена вдоль оси вращения Ох. Ө - угол между внутренней нормалью п и вектором скорости (рис. 4). Для затупленного степенного тела образующая имеет вид

0,              0 < т < т0, х (т) = ^     гР-гР               D                               (22)

I ^LЖГ^ ’ ^т 0 <^т<^R.

Сопротивление тела складывается из сопротивления плоского торца Схі с радиусом 'затупления то и поверхности вращения Сх2:

Т 2

Сх і = (р о + р і ) R 2 .

• ^т 2       ^{2             R т}         2 ^{R т}

^Сх2 = ^{Т 0} (1 - R2) ⁺ R 2 ^{(р 0 — т 0 )}.Д . . 2 ^{dT +} R2^р1 Д . . .     ""'

Используя гипергеометрическую функцию F [a,b,C’d\, можно записать (величина то отнесена к R и удлинение А = L/Rp

Сх = Сх і + Сх 2 = Т о + (р о + р і — Т о ) т 2 +

/_ғ [1 Р ( Р^ ^ ² 1 __r2_F [1 Р ( РЗГ о-1 ^ 211

• ^{+    (р 0 Т 0 )}<^{Ғ 1,}р- і ’ 5 -і ’      і -г /3         Ы^{Ғ 1}’Р- і ’ 5 -і ’        і- г Р         ⁺       ₍₂₃₎

• / _Ғ [ і ■              ^Р ^ V1   _Г2_Ғ [ і   ■           ( 5^І о± ^ 2 1!

• ^{+    рі} 1 ^F 2 ’ Р -і ’ Р -і ’   Ді-Ду        ^{Т 0 Ғ} 2 ’ Р -і ’ Р -і ’ Д і -г^Р у I

Задача свелась к нахождению минимума функции Сх по двум переменным 3 и Т0 при фиксированных параметрах А, Re0, t_w , у. В табл. 6 даны значения 3, tq, Сх - коэффициент сопротивления с затуплением то и Схо - коэффициент сопротивления без затупления в зависимости от удлинения А для разных чисел Re0- Расчеты проводились для температурного фактора t_w = 0.1 и у = 1.4.

Т а б л и ц а б

Re = 1.0					Re = 10.0				Re = 100.0
А	3	То	Сх	Схо	3	то	Сх	Схо	3	то	Сх	Схо
1	1.66	0.396	1.99	2.0	1.588	0.357	1.4	1.43	1.577	0.352	0.967	1.01
2	1.54	0.166	1.88	1.88	1.46	0.128	1.16	1.17	1.46	0.123	0.612	0.62
3	1.5	0.082	1.83	1.83	1.41	0.053	1.08	1.08	1.4	0.05	0.483	0.485
4	1.48	0.046	1.8	1.8	1.39	0.026	1.04	1.04	1.37	0.024	0.428	0.428
5	1.47	0.029	1.79	1.79	1.38	0.015	1.02	1.02	1.36	0.013	0.4	0.41
6	1.47	0.02	1.78	1.78	1.38	0.009	1.005	1.005	1.35	0.008	0.384	0.385
7	1.47	0.014	1.77	1.77	1.37	0.006	0.997	0.997	1.35	0.005	0.375	0.375
8	1.47	0.011	1.77	1.77	1.37	0.004	0.992	0.992	1.35	0.003	0.368	0.368
9	1.47	0.008	1.76	1.76	1.37	0.003	0.988	0.988	1.34	0.002	0.364	0.364
10	1.47	0.007	1.76	1.76	1.37	0.002	0.986	0.986	1.34	0.002	0.361	0.361
15	1.47	0.003	1.75	1.75	1.37	0.001	0.978	0.978	1.34	0.0005	0.353	0.353
20	1.48	0.001	1.75	1.75	1.37	0.0004	0.976	0.976	1.34	0.0002	0.35	0.35

Т а б л и ц а 7

Свободномолекулярный случай					Локальная модель Reо = 0.1
А	3см	тосм	Схсм	Схосм	3лок	толок	Схлок	СхоЛ0К
1	1.77	0.468	2.174	2.182	1.74	0.449	2.149	2.157
2	1.64	0.235	2.114	2.117	1.62	0.217	2.082	2.085
3	1.59	0.132	2.082	2.083	1.57	0.119	2.047	2.048
4	1.56	0.082	2.064	2.064	1.55	0.073	2.028	2.028
5	1.54	0.056	2.052	2.052	1.53	0.049	2.015	2.016
6	1.53	0.04	2.044	2.044	1.52	0.034	2.007	2.007
7	1.53	0.03	2.037	2.038	1.52	0.026	2.	2.
8	1.52	0.023	2.033	2.033	1.51	0.02	1.996	1.996
9	1.52	0.018	2.029	2.029	1.51	0.016	1.992	1.992
10	1.52	0.015	2.026	2.026	1.5	0.013	1.989	1.989
15	1.51	0.007	2.018	2.018	1.5	0.006	1.981	1.981
20	1.5	0.004	2.013	2.013	1.5	0.003	1.976	1.976

Т а б л и ц а 8

Локальная модель Reо = 10 000					Модель Ньютона
А	3лок	толок	Схлок	СхоЛ0К	3н	Тон	Схн	Схон
1	1.57	0.352	0.772	0.824	1.57	0.352	0.75	0.803
2	1.45	0.123	0.351	0.36	1.45	0.123	0.321	0.33
3	1.4	0.05	0.198	0.2	1.4	0.05	0.165	0.167
4	1.37	0.024	0.132	0.133	1.37	0.024	0.098	0.099
5	1.36	0.013	0.099	0.099	1.36	0.013	0.064	0.065
6	1.35	0.008	0.081	0.081	1.35	0.008	0.045	0.045
7	1.35	0.005	0.069	0.069	1.35	0.005	0.037	0.037
8	1.35	0.003	0.061	0.061	1.35	0.003	0.026	0.026
9	1.34	0.002	0.056	0.056	1.34	0.002	0.02	0.02
10	1.34	0.002	0.052	0.052	1.34	0.002	0.017	0.017
15	1.34	0.0	0.043	0.043	1.34	0.0	0.007	0.007
20	1.34	0.0	0.04	0.04	1.34	0.0	0.004	0.004

В табл. 7 представлены данные сравнения расчетов величин /3 и го, при которых коэффициент сопротивления минимален в свободномолекулярном случае и в случае расчетов локальным методом для малых чисел Re о.

В табл. 8 представлены аналогичные данные сравнения расчетов для больших чисел Re о и расчетов с помощью формулы Ньютона.

7. Заключение

Сравнение показывает, что результаты расчетов по свободномолекулярной модели газа и локальной модели при малых числах Re о близки. Отличие в Сх составляет не более 2%. И в том и другом случае при больших удлинениях величины /3 ^ 1.5. Результаты расчетов величин 3 и го по модели Ньютона и локальной модели при больших числах Reo совпадают. Отличие в величинах Сх получается в результате того, что в локальной модели учитывается трение, а в модели Ньютона нет. Особенно влияние трения сказывается при больших удлинениях.

Во всех локальных моделях течения для тел вращения со степенной образующей наличие затупления уменьшает величину аэродинамического сопротивления. Особенно этот эффект проявляется при малых удлинениях. При удлинениях А > 6 радиус затупления стремится к нулю и затупление практически не влияет на сопротивление.