Зависимость деформации роговицы от параметров системы при быстром нестационарном нагружении

RUSSIAN JOURNAL OF BIOMECHANICS

При обследовании глаза в современной клинике значительное место занимают методы, использующие кратковременное воздействие на роговицу струей сжатого воздуха. При этом центральная область роговицы, примыкающая к апексу, подвергается воздействию возрастающего внешнего давления. В широко используемых пневматических тонометрах внутриглазное давле- ние оценивается по тому напору струи, при котором некоторый центральный участок роговицы становится практически плоским. Более детальные характеристики ее поведения под нестационарным воздействием исследуются с целью последующего использования для диагностики в анализаторе реакции глаза (Ocular Response Analyzer, ORA), разработанном фирмой Reichert [1]. Этот прибор отслеживает с высоким временным разрешением (порядка миллисекунд) изменение во времени

0000-0003-4154-877X

0000-0001-9067-7717

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

внешнего давления, создаваемого струей, и определяет давления и моменты времени, при которых достигается уплощение. Нагружение роговицы в ORA продолжается некоторое время и после появления плоского участка, что позволяет в процессе последующей разгрузки фиксировать второе уплощение, для которого также определяются внешнее давление и момент времени, когда оно наблюдается.

Кривая «давление - время» в ORA симметрична. Поэтому при чисто упругом поведении системы оба момента уплощения были бы расположены на этой кривой тоже симметрично, что соответствовало бы также симметричным значениям времени и равным давлениям. Однако при достаточно быстром нагружении (в ORA весь процесс нагружения и разгрузки занимает несколько десятков миллисекунд) наблюдается асимметрия: на нисходящей ветви уплощение происходит при меньшем давлении, чем на восходящей. Это явление было названо корнеальным гистерезисом [1]. Такая асимметрия могла бы быть связана с инерционными эффектами, однако с учетом малости смещений, как было показано нами ранее [2], они оказываются несущественными. Остается предположить, как было отмечено уже разработчиками [1], что в нарушении симметрии процесса проявляются вязкоупругие свойства роговицы.

По положению точек, соответствующих на кривой «давление - время» двум моментам уплощения, определяются и выдаются прибором две основные характеристики: полусумма давлений уплощения при нагружении и разгрузке (среднее давление уплощения), эмпирически отождествляемая с внутриглазным давлением по Гольдману, и разность этих давлений, называемая величиной корнеального гистерезиса (или просто корнеальным гистерезисом). Обычно считается, что именно эта величина характеризует вязкоупругие свойства роговицы. Корнеальный гистерезис рассматривается как диагностический параметр. Накоплен значительный эмпирический материал, позволяющий рассматривать его как один из маркеров глаукомы [3–6]; этот параметр также использовался для оценки эффективности лечения последней [7]. Выполняются исследования для обоснования применения корнеального гистерезиса в сочетании с другими показателями для диагностики ранних стадий кератоконуса [8].

Помимо двух упомянутых, ORA выдает еще две эмпирически введенные характеристики: роговично-компенсированное давление и фактор резистентности роговицы [9]. Этим характеристикам, рассчитываемым с учетом толщины роговицы в центральной области, приписывается самостоятельное диагностическое значение. В настоящей работе они специально не рассматриваются.

Исследованию связи измеряемых характеристик с механическими и структурными свойствами корнеосклеральной оболочки посвящены многочисленные эмпирические исследования [10; 11]. Однако вопрос о том, каким образом измеряемые в приборе параметры соотносятся с реальными количественными механическими характеристиками системы - истинным внутриглазным давлением и величинами, характеризующими упругие и вязкоупругие свойства глазных тканей, прежде всего роговицы, на сегодняшний день остается в значительной степени открытым. Понимание такой связи создаст дополнительную (к другим методам измерения) возможность неинвазивной оценки механические свойств и механического состояния конкретного живого глаза. Такая оценка важна как для научных исследований, так и для повышения информативности клинического обследования, создавая научную базу для совершенствования методов диагностики и оценки результатов лечения.

Для решения этой задачи необходима математическая модель, которая, хорошо воспроизводя данные измерений, дала бы возможность физически корректно интерпретировать их результаты. Имеющиеся в литературе численные расчеты, основанные на громоздких конечно-элементных моделях [12; 13], оказываются тут малопродуктивны. При таком подходе необходимо знание многих констант, в первую очередь упругих, определяемых, как правило, в измерениях на трупном материале с осреднением результатов по многим глазам. Нахождению таких констант посвящены многочисленные публикации [14–17]. Между тем константы, характеризующие эти свойства, в большой степени индивидуальны, значительно изменяясь от пациента к пациенту [18], и неизвестны заранее. Что касается характеристик вязкоупругого поведения роговицы, то они зачастую берутся из данных опытов с существенно бо́льшими характерными временами [12]. Обратная задача определения констант материала роговицы решалась сочетанием расчетов методом конечных элементов с применением техники параметрического анализа [19– 21]. Однако использовавшиеся при этом модели, сохраняя значительное количество определяемых параметров, тем не менее не вполне адекватно описывали реальные особенности механического поведения роговицы.

Эффективная оценка в эксперименте механических свойств и механического состояния конкретного живого глаза требует создания физически адекватных моделей, содержащих небольшое количество представительных подлежащих определению параметров. Авторами разработан [22] максимально упрощенный подход к описанию механики глазного яблока, который оказался полезен при моделировании различных типов статической тонометрии. В рамках этого подхода роговица представляется безмоментной (мягкой) двумерной поверхностью, а склеральная область нульмерным элементом, откликающимся изменением объема на изменение внутриглазного давления. В базовом варианте роговица и склеральный сегмент считались линейно упругими, а упругие свойства роговицы как двумерной поверхности пространственно однородными и изотропными. Развитый метод легко обобщается на более сложные случаи с сохранением его основного достоинства: число определяемых параметров остается небольшим. Были рассмотрены обобщения базовой модели для пространственно неоднородной и нелинейно упругой роговицы [23; 24].

В работе [2] этот подход был применен к моделированию деформирования глазного яблока под действием внешнего давления, приложенного к роговице в ограниченной области. Задача решалась в рамках базовой линейно упругой модели. Такое приближение допустимо в ситуации достаточно медленного нагружения, когда вязкоупругие свойства несущественны, а также и при более быстрых воздействиях для грубых оценок связи между внешним и внутриглазным давлениями. Модель описывает формирование при некотором внешнем давлении области роговицы, которую с высокой точностью можно считать плоской. По этому давлению можно оценивать истинное внутриглазное давление. Упругие свойства как роговицы, так и склеральной области влияют на связь между внешним и истинным давлениями, но не слишком значительно.

Такая постановка вполне приложима к моделированию нагружения роговицы струей воздуха в пневмотонометре, когда отслеживается лишь одно ее уплощение. Однако она недостаточна для описания корнеального гистерезиса, что требует учета вязкоупругих свойств роговицы. В [2] было предложено обобщение базовой модели, рассматривающее роговицу как вязкоупругий материал фойгтовского типа, однако расчеты в рамках этого обобщения в той работе не проводились. Это было впервые сделано в [25], где показано, что модель описывает появление корнеального гистерезиса, величина которого тем выше, чем больше характерное время релаксации деформаций, определяемое соотношением вязких и упругих констант. Значения параметров, полученные при моделировании, имеют тот же порядок, что те же значения, определяемые экспериментально. Расчеты продемонстрировали зависимость величины корнеального гистерезиса от вида зависимости внешнего давления от времени: при возрастании его максимального за время опыта значения гистерезис растет.

В предлагаемой работе в рамках той же модели детально исследована зависимость среднего давления уплощения и корнеального гистерезиса от физически важных механических характеристик глаза: роговичной и склеральной жесткостей, времени релаксации деформаций роговицы (характерного времени вязкоупругости) и истинного внутриглазного давления, а также более подробно, чем в [25], от максимального нагружающего давления. Показано, что величина корнеального гистерезиса зависит от истинного давления и не может рассматриваться как характеристика, непосредственно отражающая степень вязкоупругости роговицы. Предложена методика эффективной оценки параметра, характеризующего ее вязкоупругость, по данным, определяемым в эксперименте.

Математическая модель, постановка задачи и метод решения

Используемая модель и постановка задачи о деформировании глазного яблока под действием внешнего давления, приложенного к ограниченной области роговицы, подробно рассмотрены в [2; 25].

Внешнее давление p* ( r ) предполагается распределенным в ограниченной апикальной области роговицы как функция времени и координаты в соответствии с данными, имеющимися для ORA [12]:

p . ^{( r} ) ^{= <}

Pj ( cos ( п r/r ) + 1 ) /2 ( - r <  r <  r )

0   ( r £ [ - r j , r j ])

где P j - максимальное значение действующего на роговицу давления, которое достигается при r = 0 . Далее для определенности будем называть p_j давлением в струе. Характеризовать действующее на роговицу давление можно по-разному. Однако, если соответствующая характеристика, извлекаемая из зависимости (1), имеет размерность давления, а радиус действия внешнего давления r j фиксирован, она будет отличаться от P j только постоянным множителем.

Изменение давления в струе p_j со временем будем задавать следующей функцией, описывающей динамику струйного нагружения в ORA :

1           I               tc |П

Pj ⁽ t ) = - P j mx I sin I t ^- у I- + ¹

Здесь tc - время, при котором давление в струе Pj достигает максимума pjmах. Кривая p}(t) симметрична относительно оси t = tc.

Поверхность, представляющая роговицу, считается изотропной и однородной. Для нее используются линейные определяющие соотношения, описывающие вязкоупругость фойгтовского типа, которые в пренебрежении дополнительной вязкостью, проявляющейся при изменении площади поверхности, имеют вид:

8j + Т^ =

[ T -v T - Т о (1 -v c ) ] , E_c

е 2 ^{+ Те} 2 = 7* [ ^T 2 ^-v c^T1 ^{- T} 0^{(1 -v} c ) ] • E_c

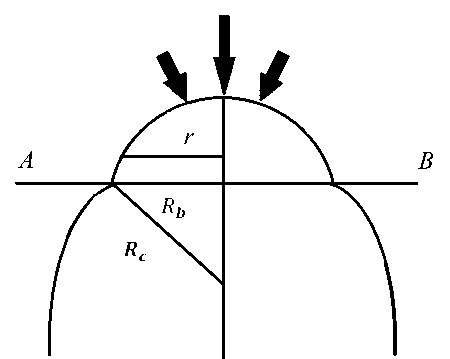
Рис. 1. К постановке задачи. Плоскость AB отграничивает роговицу от склеральной области, r – радиальная координата, R с – радиус роговицы, R b – радиус основания роговичного сегмента. Стрелки показывают область действия внешнего давления.

Здесь T и T – касательные усилия в главных (меридиональном и окружном) направлениях; Sj и s₂ - деформации в направлениях главных осей, отсчитываемые от начального состояния не нагруженной извне роговицы, в котором она имеет форму сферического сегмента с T = Т₂ = Т _о; коэффициенты E ** = 5 Е_с и v_c имеют смысл упругих модулей (модуля растяжения и коэффициента Пуассона) роговицы как двумерной упругой поверхности при медленных процессах (5 - средняя толщина роговицы, а Е_с - ее средняя жесткость); т - время релаксации деформаций роговицы ( т = ц / Е_с , где ц -фойгтовская вязкость). Точкой обозначена производная по времени.

Склеральная область рассматривается как нульмерный объект, механические свойства которого характеризуются склеральной жесткостью E [22]. Пренебрежение возможной вязкоупругостью склеральной области правомерно, поскольку жесткость склеры намного больше жесткости роговицы ( E_s >> Е_с , в норме более чем на порядок [22]). Таким образом, даже при том же порядке вязкости, время релаксации деформаций значительно меньше для склеры, чем для роговицы. Поскольку отклонение от упругого поведения системы в рассматриваемом процессе мало (соответствующее характерное время намного меньше характерного времени нагружения [1]), правомерно ожидать, что оно определяется элементом с намного бо_́льшим временем релаксации деформаций, т.е. роговицей. Суммарный объем подроговичной и склеральной областей, как всегда в задачах тонометрии, считается постоянным.

Геометрические характеристики роговицы (рис. 1) принимались равными Rc = 8 мм, Rb = 5,8 мм, что соответствует стандартным для человеческого глаза значениям. Для условной средней толщины роговицы принималось ее нормальное значение 5 = 0,5 мм. Все присутствующие в расчетах линейные размеры далее обезразмериваются по радиусу роговицы R . В расчетах радиус зоны влияния струи (т.е. области, где p, (r) отлично от нуля) r полагался равным 0,385. Эта величина соответствует размерному значению, приведенному в [12].

Параметры развертки внешнего давления во времени в дальнейшем, если не оговорено противное, выбираются следующим образом: длительность возрастания нагрузки t_c = 12,5 мс, максимум внешнего давления P jmx = ⁸⁰ мм рт. ст.

Роговичная и склеральная жесткости E и E , как и истинное давление p , варьировались в широком диапазоне их физиологических значений. Время релаксации деформаций т варьировалось вблизи значения т = 1 мс, определяющего порядок этой величины, найденный из рассмотрения экспериментальных кривых.

Метод решения подробно описан и обоснован в публикациях [2; 25]. Сначала ищется нулевое приближение: для каждого момента времени t решается чисто упругая задача в пренебрежении вязкоупругими эффектами (т = 0) при внешнем давлении pj, соответствующем этому времени. Получающаяся при этом система обыкновенных дифференциальных уравнений решается методами Рунге – Кутты четвертого порядка и стрельбы при различных внутренних давлениях р с игнорированием условия постоянства объема, а затем подбирается собственное число р, при котором это условие выполняется. Для поиска первого приближения, достаточного для эффективной оценки поведения системы, по нулевому приближению строилась система дифференциальных уравнений (также обыкновенных), для которой с использованием разностной схемы Эйлера решалась задача Коши. Далее по алгоритму, разработанному в [2] и уточненному в [25], определялись два значения внешнего давления рj (на восходящем и нисходящем участ- ках кривой Pj (t)), при которых достигается локально наибольшая степень уплощения.

Результаты численного моделирования

На рис.2 представлены основные параметры, характеризующие расположение точек, соответствующих уплощениям, на кривой Pj ( t ) .

Непосредственно моменты уплощения характеризуются давлениями уплощения p + и p - (на восходящем и нисходящем участках соответственно), а также соответствующими значениями времени t и t . По давлениям уплощения вычисляются среднее давление уплощения <  Pj >= ( p + + p- ) / 2 и корнеальный гистерезис H = p + - p - . Эти величины непосредственно выдаются ORA . Существенное значение, как мы увидим в дальнейшем, имеет время запаздывания второго уплощения, по сравнению с первым Л T = t₊ +1_ - 2 t_c (здесь t время достижения максимального внешнего давления). Величина ЛТ прибором не выдается, однако может быть определена по демонстрируемой им кривой p_} ( t ) . Имеют место соотношения: p + >  p- , H > 0 , t c = ( t + + 1 - )/2 .

На рис. 3 представлены зависимости среднего давления уплощения <  p_} >  от характерного времени вязкоупругости т при различных значениях жесткостей и истинного давления. Давление <  p_} >  растет с ростом склеральной жесткости и истинного давления, а с ростом роговичной жесткости и времени релаксации деформаций уменьшается. Как видно из рис. 3 а , б , для глаза с нормальными роговичной и склеральной жесткостями Е_с = 0,3 и E_s = 10 МПа в рассмотренном диапазоне изменения т среднее давление уплощения <  p_} >  остается близким к истинному p ₀, максимально отличаясь от него на величину порядка 1 мм рт. ст. С точностью измерений, принятой в офтальмологии, такая погрешность приемлема. Однако, если склеральная жесткость значительно превосходит нормальную, определяемое таким образом внутриглазное давление может оказаться заниженным на 2 мм рт. ст. и более. Учет реальной роговичной жесткости также может давать поправку к давлению до 2 мм рт. ст, завышая его. При синхронном возрастании обеих жесткостей (что характерно для глаз с глаукомой) их влияние на эту поправку может до известной степени взаимно компенсироваться. Влияние характерного времени вязкоупругости т на разность Л p =< p j >  - p₀ также значительно. Эта разность увеличивается с уменьшением т и возрастает с

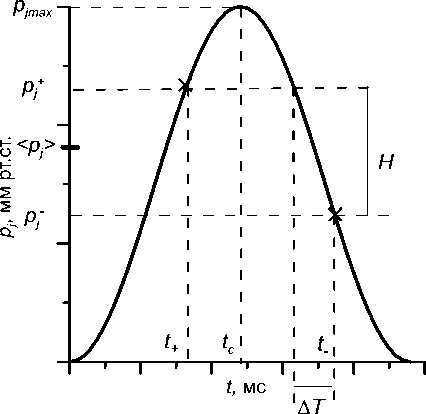
Рис. 2. Кривая p, ( t ) и основные рассматриваемые ниже параметры. Крестиками обозначены моменты уплощения.

ростом p . При нормальных жесткостях E и E величина Л p может для достаточно малых т достигать 1 мм рт. ст. при p₀ = 12 мм рт. ст. и 3 мм рт. ст. при p₀ = 24 мм рт. ст.

Как видно из рис. 3, среднее давление уплощения <  p. >  дает завышенную оценку истинного давления p 0 для всех исследованных значений т , кроме достаточно больших. Поэтому для более корректной оценки p 0 , если данных о жесткостях глазных тканей нет, имеет смысл использовать не непосредственно <  p_: > , а добавлять к этой величине некоторую положительную константу: порядка 1 мм рт. ст., если привязываться к нормальным значениям упругих констант и т = 1 мс. Желательность такой поправки была ранее отмечена в [2]. Если для характеристики внешнего давления на роговицу используется величина, отличная от p , поправка тем более целесообразна, поскольку любой такой параметр будет меньше p .

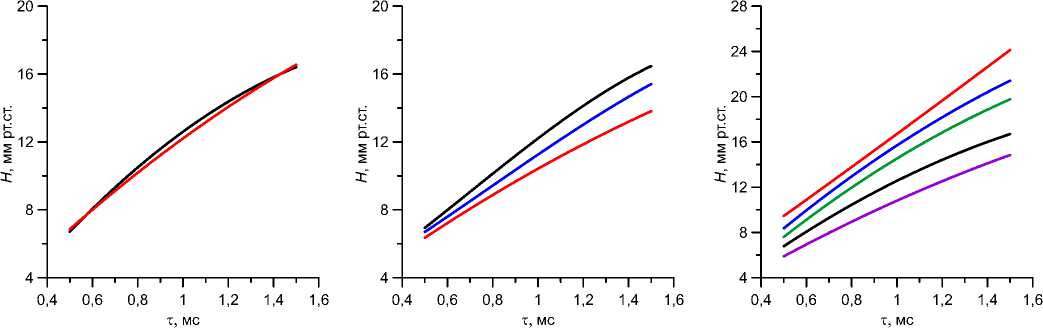
На рис. 4 показана зависимость корнеального гистерезиса H от характерного времени вязкоупругости т при различных значениях обеих жесткостей и истинного давления. Зависимость H от склеральной жесткости (рис. 4, а ) практически отсутствует, влияние роговичной жесткости более заметно, но при т <  1 мс не слишком велико (рис. 4, б ): за счет ее физиологически возможных изменений H меняется не более чем на 2 мм рт. ст. Однако при т >  1 мс поправка может оказаться вдвое большей. Наиболее существенное влияние на гистерезис оказывает истинное давление (рис. 4, в ): поправка при больших т может достигать 100 %. Таким образом, в противовес традиционному представлению,

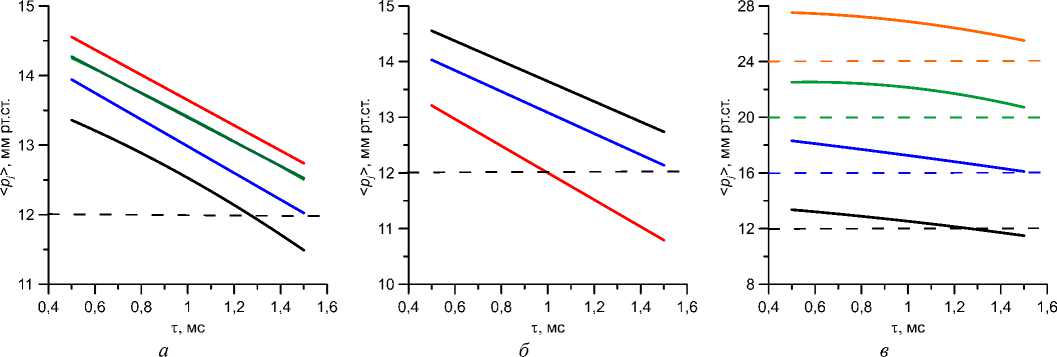
Рис. 3. Зависимость среднего давления уплощения <  Pj >  от характерного времени вязкоупругости т при различных

склеральной E_s ( а ) и роговичной Е_с ( б) жесткостях, а также от истинного давления р ₀ ( в ).

На рисунке фиксированы значения Е_с = 0,3 МПа, р₀ = 12 мм рт. ст. ( а ); E_s = 80 МПа, р₀ = 12 мм рт. ст. ( б) ;

Е_с = 0,3 МПа, E_s = 10 МПа ( в ). Кривые соответствуют снизу вверх E_s = 10,20, 40, 80 МПа ( а );

Е_с = 0,9,0,6, 0,3 МПа ( б) ; р₀ = 12, 16, 20, 24 мм рт. ст. ( в );

а, б - горизонтальный пунктир показывает истинное давление; в - каждый горизонтальный пунктир показывает истинное давление р ₀, соответствующее кривой того же цвета.

а                                      б                                       в

Рис. 4. Зависимость корнеального гистерезиса H от характерного времени вязкоупругости т при различных скле-

ральной e ( а ) и роговичной e ( б ) жесткостях, а также от истинного давления р ₀ ( в ).

а: Е_с = 0,3 МПа, р₀ = 12 мм рт. ст.; б: E_s = 80 МПа, р₀ = 12 мм рт. ст.; в: Е_с = 0,3 МПа, E_s = 10 МПа.

Кривые снизу вверх соответствуют: а - E_s = 80 , 10 МПа; б - Е_с = 0,9,0,6, 0,3 МПа;

в - p ₀ = 10, 12, 16, 20, 24 мм рт. ст.

величина корнеального гистерезиса в отдельности никак не может рассматриваться как характеристика вязкоупругих свойств роговицы.

С другой стороны, время запаздывания AT практически не зависит от истинного давления р ₀ (рис. 5, в ). Хотя эта величина все же зависит, весьма слабо, от склеральной жесткости (рис. 5, а ) и несколько более заметно от роговичной (рис. 5, б ), она оказывается наиболее адекватной характеристикой собственно вязкоупругих свойств роговицы. Время AT всегда больше т . Очень грубо, по порядку величины, характерное время вязкоупругости может оцениваться как т ~ A T / 2.

Время запаздывания AT не входит в число характеристик, выдаваемых ORA , однако оно может быть непосредственно определено по кривой «внешнее давление - время» (корнеограмме). Величина AT не зависит от того, каким образом выбран параметр, характеризующий внешнее давление на границе с роговицей (это не обязательно используемое нами максимальное давление p j ), и в каких единицах оно измеряется.

Возможна также оценка характерного времени вязкоупругости т по корнеальному гистерезису, но с учетом среднего давления уплощения. На рис. 6 представлена зависимость гистерезиса H от среднего давления уплощения <  р_} >  при различных характерных

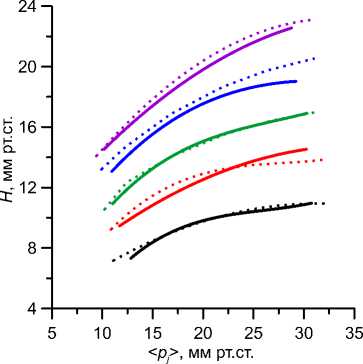
Рис. 6. Зависимость корнеального гистерезиса H от среднего давления уплощения <  р_} >  при различных характерных временах вязкоупругости Т . Склеральная жесткость E = 10 МПа, роговичная жесткость

Е_с = 0,3 МПа для сплошных кривых и 0,7 МПа для пунктирных; кривые снизу вверх (сплошные и пунктирные отдельно) соответствуют τ = 0,6, 0,8, 1, 1,2, 1,4 мс.

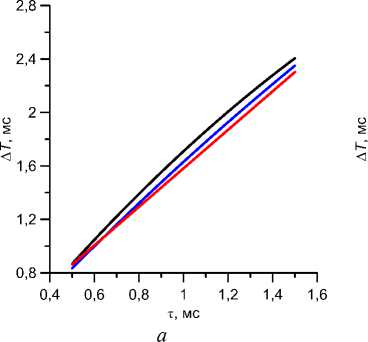
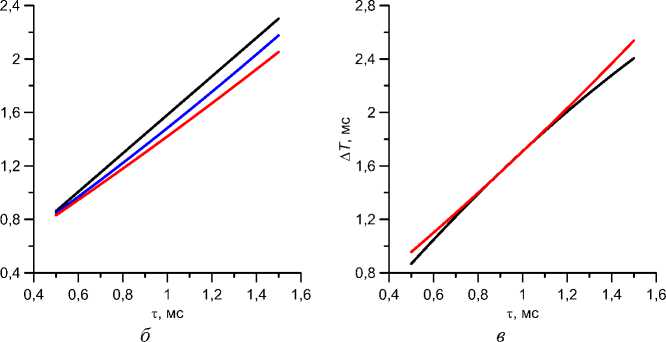
Рис. 5. Зависимость времени запаздывания Л T от характерного времени вязкоупругости т при различных склеральной E ( а ) и роговичной E ( б ) жесткостях, а также от истинного давления p ( в );

а - Е_с = 0,3 МПа, р₀ = 12 мм рт. ст.; б - E_s = 80 МПа, р₀ = 12 мм рт. ст.; в - Е_с = 0,3 МПа, E_s = 10 МПа;

в - показаны почти совпадающие кривые с р₀ = 12 (нижняя) и 24 мм рт. ст.;

кривые сверху вниз соответствуют: а - E_s = 10,20, 80 МПа; б - Е_с = 0,3,0,6, 0,9 МПа.

временах вязкоупругости т и двух значительно различающихся значениях роговичной жесткости. Склеральная жесткость, зависимостью от которой характеристик < р} > и H, как показано выше, практически можно пренебречь, фиксирована: Es = 10 МПа. Зависимость от истинного давления p в представленных кривых исключена и отсутствует. По положению точки, соответствующей измеренным значениям < р} > и H, можно после соответствующей аппроксимации оценить, на какую кривую она попадает, и тем самым оценить параметр т , характеризующий степень вязкоупругости роговицы. Близость сплошных и соответствующих пунктирных кривых на рис. 6 позволяет при этом пренебрегать влиянием не только склеральной, но и роговичной жесткости. При таком способе оценки т, как и при определении этой величины из корнеограммы по времени запаздывания, результат не зависит от единиц, в которых измерено внешнее давление и от способа его определения.

В приводимой таблице представлены результаты применения описанных методов к расчету характерного времени вязкоупругости т по данным, полученным для конкретных глаз [1]. Каждая строчка соответствует индивидуальной корнеограмме, для которой приведены величина гистерезиса H , среднее давление уплощения <  Pj >  , время запаздывания ЛТ и значения параметра т , рассчитанные двумя способами: т - по Л Т и зависимости Л Т (т) (рис. 5, в ) и т - по <  р_} >  и H в соответствии с алгоритмом, описанным выше. Из таблицы видно, что оба способа дают близкие значения т . Для конкретных роговиц этот параметр может значительно различаться (вдвое и более).

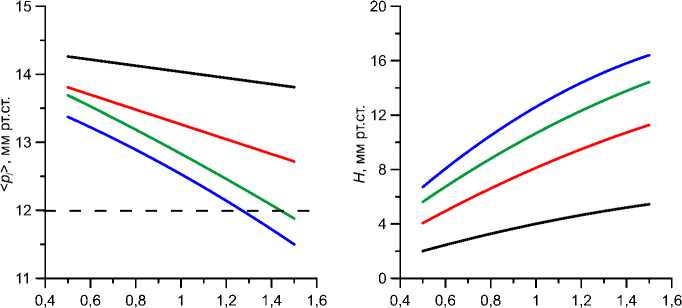
В приведенных до сих пор расчетах менялись только параметры глаза, тогда как параметры кривой p ( t ) оставались неизменными. Изменение этих параметров меняет распределение скоростей деформаций во времени и не может не сказаться на результатах. На рис. 7 показано влияние максимального внешнего давления p j max на основные характеристики процесса деформирования: среднее давление уплощения <  р_} > , величину корнеального гистерезиса H и время запаздывания ЛТ . При этом длительность воздействия остается неизменной: t c = 12,5 мс. И среднее давление уплощения, и гистерезис довольно заметно зависят от p j max : первое с ростом p j max падает, второй растет. Разница между значениями    каждого    из    этих    параметров

т, мс                                             т, мс а                                  б

Рис. 7. Зависимость среднего давления уплощения <  р_} >  ( а ), величины гистерезиса H ( б) и времени запаздывания A T ( в ) от характерного времени вязкоупругости т при различном максимальном внешнем давлении р_{]т ах}; а , б - кривые соответствуют максимальному давлению p_Jmж = 20,40, 60, 80 мм рт. ст., которое

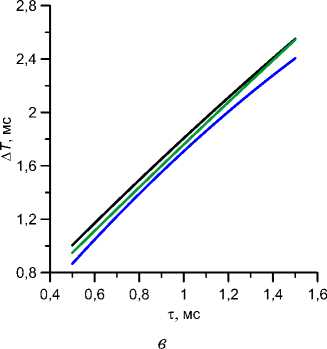
возрастает на рис. а сверху вниз, а на рис. б снизу вверх; на рис. в - p_Jm^ = 20,60, 80 мм рт. ст., возрастая сверху вниз. На всех рисунках Е_с = 0,3 МПа, E_s = 10 МПа, р₀ = 12 мм рт. ст.

Результаты расчетов для конкретных глаз

N H, мм рт.ст <Р]>, мм рт.ст Л T, мс Т1, мс Т2, мс 1 16,7 14,7 2,1 1,25 1,3 2 10,7 16,5 1,3 0,75 0,75 3 7 17,3 1,2 0,7 0,5 4 12,1 36,4 0,9 0,5 0,6 5 8,4 40,1 1,1 0,6 0,5 6 14 14,7 2,15 1,3 1,1 при PJm ах = 20 и 80 мм рт. ст. увеличивается с ростом т и достигает при т = 1,5 величины порядка 2,5 мм рт. ст. для < р} > и 12 мм рт. ст. для H (H при этом увеличивается в 4 раза). С возрастанием максимального давления этот эффект становится менее заметным: разница между значениями при pjmах = 60 и 80 мм рт. ст. имеет порядок 0,5 мм рт. ст. для < р} > и 1-2 мм рт. ст. для H ( H возрастает не более чем на 20 %). Время запаздывания AT при изменении максимального давления от 20 до 80 мм рт. ст. меняется незначительно, что лишний раз подтверждает возможность эффективной оценки по этой величине вязкоупругих свойств материала роговицы. Как показано выше, характерное время вязкоупругости т может не только оцениваться непосредственно по AT, но и рассчитываться (независимо от величины р]тш ) по двум параметрам < р} > и H . Алгоритм такого расчета от p не зависит.

Заключение

В результате математического моделирования показано, что среднее внешнее давление уплощения (полусумма давлений уплощения при нагружении и разгруз- ке), хотя и может быть использовано для оценки истинного внутриглазного давления, зависит от индивидуальных механических (упругих и вязкоупругих) характеристик глазных тканей. Соответствующие поправки, как правило, не слишком велики, но могут оказаться заметными для глаз, свойства которых значительно отличаются от нормальных.

Величина корнеального гистерезиса, обычно рассматриваемая как характеристика вязкоупругих свойств роговицы, мало зависит от упругих свойств глазных тканей, но сильно зависит от внутриглазного давления. Таким образом, эта величина в общем случае непригодна для непосредственной оценки собственно вязкоупругих свойств роговицы. Встречающееся в литературе утверждение, что величина гистерезиса не зависит от внутриглазного давления [1], обосновывалось эмпирически не для конкретных глаз, а в результате статистической обработки данных, полученных для многих испытуемых. Кроме того, рассматривался диапазон давлений, подавляющая часть которого находилась в области аномально высоких значений. В настоящей работе столь высокие давления не рассматривались.

Вязкоупругие свойства роговицы могут быть оценены по времени запаздывания уплощения, которое не входит в число параметров, выдаваемых ORA , но может быть в принципе определено по получаемым кривым

(без привлечения других характеристик). Оценить характерное время вязкоупругости можно также по величине гистерезиса и среднему давлению уплощения, причем способ такой оценки, как и расчет этого времени непосредственно по корнеограмме, не зависит ни от единиц, в которых измеряется внешнее давление, ни от способа его определения.

Способ определения внешнего давления в ORA конкретно не указан, а пересчет этого давления в миллиметры ртутного столба основан на сопоставлении среднего давления уплощения с результатами измерения внутриглазного давления по Гольдману в некоторой группе испытуемых, что связано со значительным произволом. Поскольку предложенные методы расчета характерного времени вязкоупругости роговицы применимы независимо от выбора меры давления, для расчета этого времени вполне пригодны данные, непосредственно выдаваемые ORA . Оба метода дают практически совпадающие результаты, что продемонстрировано на корнеограммах, полученных для конкретных глаз. Эта величина для разных роговиц может значительно различаться: вдвое и более. Она оказывается, таким образом, физически представительной мерой механического состояния конкретной роговицы, связанного с ее структурой. Поэтому ее определение представляется важным элементом при разработке диагностических методов.

В дальнейшем предполагается разработать более подробную модель, учитывающую пространственную неоднородность роговицы. Такая модель позволит