Зависимость медианы критической частоты F2-слоя на средних широтах от геомагнитной активности

госрочного прогноза ионосферы [Zolesi, Cander, 2014]. Например, базовый вариант международной модели ионосферы IRI дает именно foF2med [Bilitza et al., 2014]. Зависимость foF2med от солнечной актив- ности учтена во всех известных моделях ионосферы, включая IRI, с помощью индексов солнечной активности или эффективных ионосферных индексов. Эффективный ионосферный индекс определяется по экспериментальным значениям foF2med так, чтобы минимизировать ошибку foF2med при замене обычного индекса солнечной активности на ионосферный индекс [Liu et al., 1983; Caruana, 1990; Mikhailov, Mikhailov, 1995]. Во многих случаях такая замена позволяет увеличить точность прогноза foF2med для конкретной станции [Liu et al., 1983; Caruana, 1990; Mikhailov, Mikhailov, 1995]. Данное преимущество эффективного ионосферного индекса объясняют тем, что изменения foF2med с циклом солнечной активности зависят не только от уровня этой активности, но и от ряда других факторов, включая геомагнитную активность, которые неявно учтены в ионосферном индексе.

Явная зависимость f oF2_med от геомагнитной активности анализировалась только в нескольких работах и была основана на поиске зависимости f oF2 med от Ap m — среднего за данный месяц [Sole, 1998] или Ap 12 — среднего за 12 месяцев [Xu et al., 2008] значения Ap -индекса геомагнитной активности. Кроме того, зависимость от геомагнитной активности учитывалась при анализе долговременных изменений f oF2 med [Bremer, 1998; Laštovička et al., 2006; Mielich, Bremer, 2013] . В указанных работах предполагались линейные или нелинейные зависимости f oF2 med от индексов солнечной и геомагнитной активности.

Возможен и другой подход к оценке вклада геомагнитной активности в f oF2_med. Он основан на анализе зависимости отношения f oF2 med / f oF2 q от геомагнитной активности, где f oF2_q — критическая частота F2-слоя для спокойных условий, которая зависит от солнечной активности и не зависит от геомагнитной. Это позволяет приближенно считать, что отношение f oF2_med/ f oF2_q зависит только от геомагнитной активности для фиксированных месяца года и мирового времени. Аналогичный подход использовался для анализа эффектов геомагнитных бурь в относительных изменениях критической частоты F2-слоя или концентрации максимума этого слоя [Pietrella, Perrone, 2008; Pietrella, 2012; Деминов и др., 2015] .

Главной целью настоящей работы были первые оценки возможности использования такого подхода для выделения вклада геомагнитной активности в f oF2_med. При этом мы стремились сохранить прогностическую направленность f oF2 med через учет индексов солнечной и геомагнитной активности, для которых возможен долгосрочный прогноз. Ниже приведены результаты, полученные путем анализа данных ионосферной станции Слау (Slough, 51.5° N, 0.6° W) для местных полудня и полуночи за 1954–1995 гг. Последовательно представлены методика выделения вклада геомагнитной активности в f oF2 med , результаты анализа этого вклада, обсуждение и основные выводы.

МЕТОДИКА

На первом этапе необходимо построить эмпирическую модель критической частоты F2-слоя для спокойных условий — модель foF2q. Эта модель представлена в виде уравнения foF2q=c0+c1F12+c2F212 (1) с набором коэффициентов cj (j=0, 1, 2) для каждого часа мирового времени (UT) с дискретностью час и каждого месяца года (M=1 — январь, M=12 — декабрь), где F12 — среднее за двенадцать месяцев (центрированное на данный месяц) значение потока солнечного радиоизлучения на длине волны 10.7 см.

Коэффициенты cj уравнения (1) для каждого фиксированного значения UT и M определяются по массиву данных foF2 (в нашем случае это часовые значения foF2, полученные на ст. Слау в 1954–1995 гг.), из которого исключаются данные, которые не удовлетворяют условию ap(τ)<7, (2) где ap(τ) — средневзвешенное значение ap-индекса геомагнитной активности с характерным временем T=14 ч или τ=exp(–3/T)≈0.8 [Wrenn, 1987]:

ap (τ)=(1–τ)( ap ₀+ ap _–1τ+ ap _–2τ²+…), (3) ap 0 , ap –1 и т. д. — значения ap -индекса в данный, предыдущий и т. д. трехчасовые интервалы. Индексы ap определены с интервалом 3 ч, и величина τ =exp(–3/ T ) показывает, во сколько раз уменьшается вклад в ap (τ) предыдущего значения ар -индекса по сравнению с данным значением на таком трехчасовом интервале. Тем самым учтено, что ионосфера средних широт реагирует на изменение геомагнитной активности как слабо пропускающий фильтр, сглаживая отклик параметров ионосферы с характерным временем T , и отклик в каждый момент времени зависит от предыстории изменения геомагнитной активности.

Кроме индекса солнечной активности F 12 , в задачах долгосрочного прогноза ионосферы используется индекс R 12 — среднее за 12 месяцев (центрированное на данный месяц) относительное число солнечных пятен [Zolesi, Cander, 2014] . Индекс F 12 точнее индекса R 12 для построения медианы f oF2 [Deminov, 2016] . Заметим, что для построения эмпирической модели f oF2 q использовались и более точные индексы солнечной активности, включая ежедневные значения потока радиоизлучения Солнца на длине волны 10.7 см [Deminov et al., 2009] . В данном случае выбор индекса F 12 связан с возможностью использования эмпирической модели (1) для долгосрочного прогноза f oF2_q на основе прогноза F ₁₂.

Индекс ap(τ) и его аналоги использовались как индикаторы вклада геомагнитной активности в параметры термосферы [Picone et al., 2002] и foF2 [Wrenn, Rodger, 1989; Shubin, Anakuliev 1995; Fuller-Rowell et al., 2000; Kutiev, Muhtarov, 2001, 2003; Pietrella, Perrone, 2008; Pietrella, 2012; Deminov, Deminova, 2015; Деминов и др., 2015] в периоды геомагнитных бурь, но не суббурь [Deminov et al., 2013]. В указанных выше работах значения τ изменяются в пределах от 0.7 до 0.9, и принятое нами τ≈0.8 соответствует среднему из этих значений. Критерий (2) для спокойной ионосферы аналогичен приведенным в работах [Pietrella, Perrone, 2008; Deminov et al., 2009; Pietrella, 2012]. Этот критерий, по-видимому, является оптимальным компромиссом между стремлением исключить из рассмотрения все магнитовозмущенные периоды и сохранить достаточно большой массив данных foF2q для получения надежных статистических оценок коэффициентов уравнения регрессии (1). В данном случае число значений foF2q для вычисления коэффициентов уравнения (1) изменялось от 215 до 395 для разных месяцев и часов UT.

Реализация первого этапа этой методики дает эмпирическую модель (1), в которой коэффициенты модели известны. Это позволяет определить значения f oF2_q над данной станцией для любого мирового времени и месяца по известным значениям F ₁₂. На следующем этапе необходимо построить эмпирическую модель зависимости относительных отклонений медианы критической частоты F2-слоя в процентах

5 f oF2 =

' f0F2med l /0F2q

- 1 100

от геомагнитной активности. Эта модель имеет вид уравнения

δ f oF2= a ₀+ a ₁ Ap _m                              (5)

с набором коэффициентов a 0 и a 1 для каждого часа UT и месяца года M , где Ap m — среднее за месяц значение Ap -индекса геомагнитной активности. Коэффициенты a ₀ и a ₁ этого уравнения для каждого фиксированного значения UT и M определяются по массиву данных f oF2_med ст. Слау за 1954–1995 гг. (при известных f oF2 q и Ap m ), из которого исключаются данные, которые не удовлетворяют условию

Ap m <32.                                      (6)

Согласно массиву индексов Ap m за 1954–1995 гг., нарушение условия (6) наблюдалось менее чем в 2 % случаев. Кроме того, медиане f oF2 обычно соответствует относительно низкая геомагнитная активность [Deminov, Deminova, 2015] . Поэтому условие (6) позволяет получить типичные средние зависимости 5 f oF2 от Ap m , без сильных и редких отклонений.

Кроме модели (5), дополнительно была построена модель, которая описывается уравнением регрессии

δ f oF2 12 = b 0 + b 1 Ap 12                                 (7)

для каждого часа мирового времени и месяца года, где 5 foF2 12 и Ap ₁₂ — скользящие средние за двенадцать месяцев значения 5 foF2 и Ap _m для данного часа UT, центрированные на данный месяц.

Ниже представлены результаты анализа свойств уравнений (5) и (7) по данным ст. Слау за 1954– 1995 гг. для полудня и полуночи. Долгосрочный прогноз геомагнитной активности связан с определенными сложностями [Joselyn, 1995] . Можно указать только общие тенденции ее изменения. Одна из этих тенденций заключается в существовании полугодовых изменений геомагнитной активности с максимумами в равноденствия [Cliver et al., 2002] , и эту тенденцию можно учесть с помощью индекса Ap m . Другая тенденция связана с изменениями геомагнитной активности с циклом солнечной активности,

Dependence of the F2-layer critical frequency median … и эти изменения можно учесть с помощью индекса Ap ₁₂ [Echer et al., 2004] . Выбор индексов Ap _m и Ap ₁₂ в уравнениях (5) и (7) основан на таких оценках.

РЕЗУЛЬТАТЫ АНАЛИЗА

На рис. 1 показаны годовые изменения средних (в интервале 1954–1995 гг.) значений индекса геомагнитной активности Ap ave для каждого месяца, коэффициента a ₁ уравнения (5) и коэффициента корреляции K между вычисленными по этому уравнению и измеренными значениями 5 foF2 для полудня и полуночи. Ниже для краткости изложения коэффициент K назван коэффициентом корреляции уравнения (5). При вычислении Ap ave учтено условие (6), т.е. исключены данные Ap m , которые не удовлетворяют этому условию. Коэффициенты a 1 и K получены по данным ст. Слау за 1954–1995 гг. по приведенной выше методике.

На рис. 1 видны полугодовые вариации Ap ave с максимумами в равноденствия c преобладающим максимумом весной. Весной относительно высокие значения наблюдались в течение наиболее продолжительного времени. Например, условие Ap ave >15 было выполнено в течение четырех месяцев в первую половину года (с февраля по май) и двух месяцев во вторую половину года (сентябрь и октябрь).

В полдень зимой коэффициент a 1 >0, т.е. увеличение индекса геомагнитной активности приводит к увеличению 5 foF2 и, следовательно, f oF2_med, поскольку f oF2_q не зависит от геомагнитной активности (см. рис. 1 и уравнения (4) и (5)). Такое изменение 5 foF2 — положительное возмущение f oF2_med, связан-

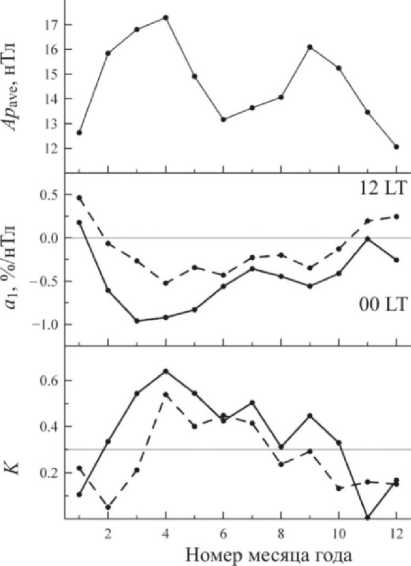
Рис. 1. Годовые изменения средних значений индекса геомагнитной активности Ap _ave, коэффициента a ₁ и коэффициента корреляции K уравнения (5) для полуночи (00 LT, сплошные линии) и полудня (12 LT, штриховые линии)

ное с ростом геомагнитной активности. Для всех остальных месяцев в полдень и полночь характерно отрицательное возмущение f oF2 med (коэффициент a 1 <0) с более высоким значением | a 1 | в полночь. В течение зимы в полночь величина a 1 может менять знак: a ₁≈0 в ноябре, a ₁<0 в декабре и a ₁>0 в январе.

Годовые изменения коэффициента корреляции K уравнения (5) для полдня и полуночи во многом подобны годовым изменениям Ap ave : они максимальны в апреле и в среднем минимальны зимой, но летом наблюдается дополнительный максимум K , который отсутствует для Ap _ave (см. рис. 1). Статистический анализ по критерию Фишера показал, что зависимость (5) значима для K >0.3 при доверительном уровне 95 % [Ramachandran, Tsokos, 2009] . Можно видеть (рис. 1), что для полуночи зависимость δ f oF2 от Ap m не значима зимой (ноябрь, декабрь и январь) и значима во все остальные месяцы года. Для полудня зависимость δ f oF2 от Ap m значима в более узком интервале — с апреля по июль, поскольку в среднем коэффициент корреляции K для полудня меньше, чем для полуночи. На рис. 1 можно видеть также, что в полночь и полдень для значимых зависимостей выполнено условие a 1 <–0.3 %/нТл, т.е. значимыми являются только достаточно отчетливые отрицательные возмущения f oF2 med , связанные с ростом геомагнитной активности.

Рисунок 2 позволяет более наглядно судить о характере зависимости δ f oF2 от Ap _m в январе, апреле и июле для полудня и полуночи. Здесь σ — стандартное отклонение измеренных значений δ f oF2 от вычисленных по уравнению (5).

Из данных на рис. 1 и рис. 2 можно видеть, что в январе значения Ap _m были меньше 20 нТл при среднем значении Ap ave =12.6 нТл. Эти значения Ap m были слишком низкими, чтобы привести к систематическим отклонениям δ f oF2 от спокойного уровня, поэтому в январе зависимость δ f oF2 от Ap _m не значима для полудня и полуночи. В апреле значения Ap _m достигали 30 нТл при среднем значении Ap _ave=17.3 нТл, что обеспечивало относительно высокий средний уровень геомагнитной активности и широкий диапазон ее изменения. Поэтому в апреле зависимость δ f oF2 от Ap _m значима для полудня и полуночи. Для полуночи эта зависимость наиболее отчетлива, обеспечивая самое высокое значение коэффициента K =0.64 в течение года (см. рис. 1). В июле значения Ap _m могли даже превышать 30 нТл, но среднее значение было относительно низким ( Ap ave =13.6 нТл) и повышенные значения Ap m наблюдались реже, чем в апреле. Возможно, что по этой причине в июле зависимость δ f oF2 от Ap m значима, но менее отчетлива, чем в апреле.

Для полуночи зависимость δ f oF2 от Ap _m значима почти в течение всего года. Исключение составляют только зимние месяцы. Поэтому можно ожидать, что для полуночи будет также значима линейная зависимость δ f oF2 12 от Ap 12 (см. уравнение (7)), где δ f oF2₁₂ и Ap ₁₂ — скользящие средние за 12 месяцев значения δ f oF2 и Ap m , центрированные на данный месяц. Явный вид уравнения регрессии (7), полученный по данным ст. Слау для полуночи за все месяцы года в интервале 1954–1995 гг.:

δ f oF2 12 =2.3–0.51 Ap 12 ±2.3, K =0.65, (8) где K — коэффициент корреляции между вычисленными по этому уравнению и измеренными значениями δ f oF2 12 . Аналогичное уравнение регрессии для полудня:

δ f oF2 12 =1.5–0.24 Ap 12 ±1.7, K =0.49. (9) Из значений коэффициента корреляции K следует, что зависимость δ f oF2 12 от Ap 12 значима для полуночи и полудня и для полуночи эта зависимость более отчетлива, чем для полудня. Это следует и из более высокого абсолютного значения коэффициента b ₁ для полуночи в этих уравнениях: b ₁=–0.51, тогда как для полудня b 1 =–0.24. Можно видеть также, что для δ f oF2₁₂ характерно отрицательное возмущение (коэффициент b ₁<0) в полдень и полночь. Это связано с выполнением условия a 1 <0 в уравнении (5) в полдень и полночь в течение почти всего года, за исключением, возможно, зимних месяцев (см. рис. 1).

Более наглядно о характере зависимости δ f oF2 12 от Ap ₁₂ можно судить по данным на рис. 3. Видно (рис. 3), что значения δ f oF2 12 в основном лежат в диапазоне –10–0 % в полночь и –5–0 % в полдень и уравнения регрессии (8) и (9) отражают эту закономерность. Следовательно, в полдень и полночь типичные отклонения δ f oF2 12 от фонового значения, связанные с ростом индекса геомагнитной активности Ap ₁₂, не превышают 5 и 10 %. Такие слабые отклонения во многих случаях можно не учитывать. Их целесообразно учитывать лишь при анализе эффектов в ионосфере с относительно низкой амплитудой, включая долговременные изменения и эффекты землетрясений.

Итак, результаты анализа медиан критической частоты F2-слоя f oF2 med на примере данных ст. Слау за 1954–1995 гг. для полудня и полуночи позволили установить, что зависимость f oF2 med от геомагнитной активности выделяется достаточно отчетливо, если использовать δ f oF2 — относительные отклонения этих медиан от спокойного уровня. Для равноденствий и лета увеличение среднего за месяц индекса геомагнитной активности Ap m приводит к уменьшению δ f oF2. Для полуночи эта закономерность более отчетлива, чем для полудня. Данная закономерность сохраняется и для средних за год значений Ap m и δ f oF2.

ОБСУЖДЕНИЕ

В приведенной методике выделения зависимости медианы критической частоты F2-слоя за месяц f oF2 med от геомагнитной активности использованы приближенные индексы солнечной и геомагнитной активности F ₁₂, Ap _m и Ap ₁₂ (см. уравнения (1), (5) и (7)), для которых возможен долгосрочный прогноз. Эти индексы, по-видимому, являются оптимальными для долгосрочного прогноза f oF2 med . Данный вывод основан на результатах сопоставления точных индексов P и ap ( τ ) с приближенными индексами F 12 и Ap _m, где P = F ₁+ F ₈₁, F ₁ и F ₈₁ — поток солнечного радиоизлучения на длине волны 10.7 см в данный день и среднее за 81 день значение этого потока, центрированное на данный день, индекс ap ( τ ) определен

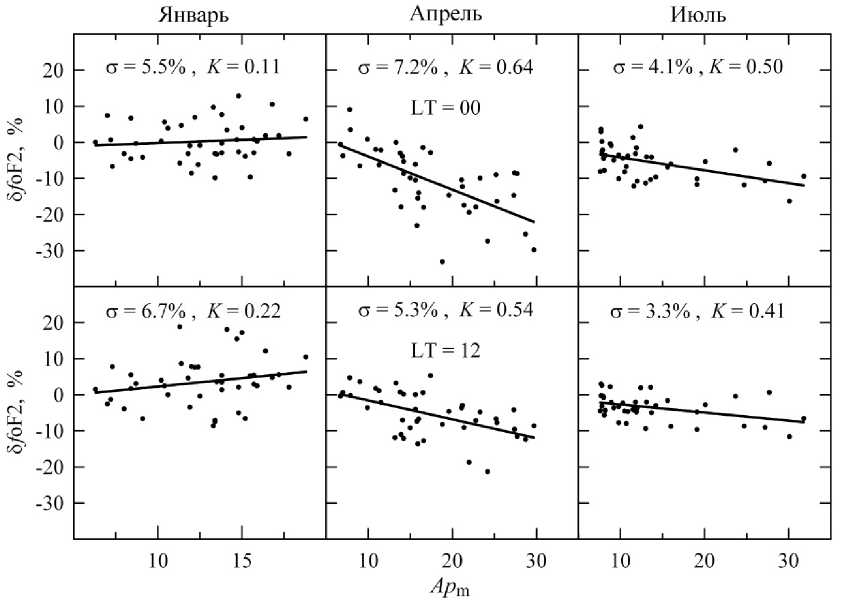
Рис. 2. Зависимости относительных значений медианы критической частоты F2-слоя δ f oF2 от Ap _m для трех месяцев года в полночь (верхняя панель) и полдень (нижняя панель): точки — по данным ст. Слау за 1954–1995 гг.; сплошные линии — по уравнению регрессии (5)

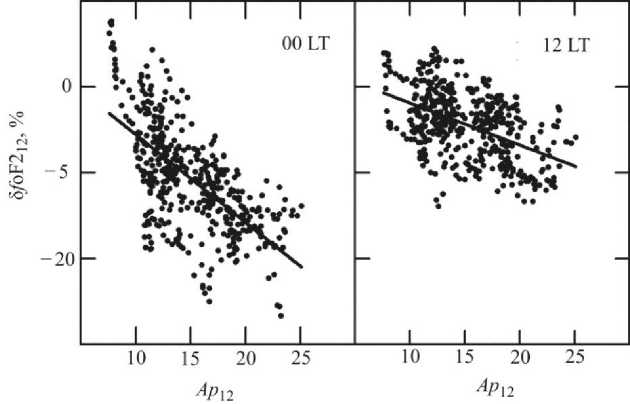
Рис. 3. Зависимость скользящих средних за год значений δ f oF2₁₂ от Ap ₁₂ в полночь (00 LT) и полдень (12 LT): точки — по данным ст. Слау за 1954–1995 гг.; сплошные линии — по уравнениям регрессии (8) и (9)

уравнением (3) для τ≈0.8 [Deminov, Deminova, 2015]. Медиана foF2 для конкретного месяца при фиксированном мировом времени соответствует конкретному дню этого месяца (при нечетном числе измерений foF2 в течение этого месяца), для которого foF2=foF2med, и точные индексы активности определены для этого конкретного дня месяца. На основе анализа данных ст. Слау за 1954–1995 гг. было получено, что нет систематической разницы между точным и приближенным индексами солнечной активности и, например, для полудня P≈1.0 F12±15 с коэффициентом корреляции K=0.96 [Deminov, Deminova, 2015]. Поэтому индекс F12 является достаточно адекватным индикатором солнечной активности в задачах долгосрочного прогноза foF2med. На основе приведенных в работе [Deminov, Deminova, 2015] результатов можно заключить, что существует систематическое различие между ap(τ) и Apm и в среднем ap(τ)≈0.8Apm во все месяцы года. Следовательно, существует определенная зависимость ap(τ) от Apm, что позволяет использовать индекс Apm в качестве индикатора геомагнитной активности для долгосрочного прогноза foF2med.

Для выделения спокойных условий здесь принято неравенство ap(τ)<7, которое совпадает с принятым в работах [Pietrella, Perrone, 2008; Deminov et al., 2009; Pietrella, 2012]. Во многих случаях считается, что спокойным условиям соответствуют случаи ap(τ)<9 [Fuller-Rowell et al., 2000; Деминов и др., 2015]. Дополнительный анализ показал, что оба эти условия приводят к почти совпадающим результатам для ст. Слау.

Отклонения f oF2 (в процентах) от спокойного уровня, связанные с геомагнитными бурями, обладают рядом закономерностей: на средних широтах во все часы суток они более положительны местной зимой, чем местным летом; для равноденствий и лета эти отклонения в основном отрицательны и в полночь они больше, чем в полдень [Buonsanto, 1999] . Отрицательные отклонения f oF2 от спокойного уровня в период геомагнитной бури называют также отрицательной фазой ионосферной бури. Эту фазу ионосферной бури объясняют соответствующими изменениями температуры и состава термосферы [Buonsanto, 1999] . Полученные по данным ст. Слау отклонения медианы f oF2 от спокойного уровня обладают аналогичными свойствами: они отрицательны во все сезоны, за исключением зимы, и при прочих равных условиях такие отрицательные отклонения в полночь больше, чем в полдень (см. рис. 1 и 2).

Разница между свойствами ионосферной бури и отклонений медианы f oF2 от спокойного уровня скорее количественная и обусловлена тем, что для медианы f oF2 по данным ст. Слау в основном выполнено условие Ap <32, а к ионосферной буре обычно относят возмущения, для которых Ap >48. В результате эффекты геомагнитных возмущений для медианы f oF2 не превышают 35 % (см. рис. 2), для ионосферных бурь они могут быть на порядок больше [Buonsanto, 1999] . Уравнение регрессии (5), которое отражает линейную зависимость δ f oF2 от Ap m для медианы f oF2, получено с учетом относительно низких амплитуд изменений δ f oF2. Для эффектов ионосферных бурь эти зависимости представляются в виде [Wrenn, Rodger, 1989; Pietrella, 2012]

ln( f oF2/ f oF2 q )=exp( c 0 + c 1 ap (τ)).

В линейном случае данное уравнение имеет вид (5) при заменах f oF2 на f oF2 med и ap ( τ ) на Ap m , косвенно показывая, что зависимости медианы f oF2 от геомагнитной активности и эффекты ионосферных бурь обусловлены одними и теми же причинами.

Диапазон изменений индекса Apm в значительной степени определяет свойства зависимостей δfoF2 от Apm для медианы foF2. В зимние месяцы (декабрь, январь, февраль) средние значения Apave и диапазон изменений Apm минимальны. Точные значения индексов геомагнитной активности ap(τ) для медианы foF2 еще меньше, например, для декабря Apave=12.1 и ap(τ)=0.8Apave=9.7. Условие ap(τ)<9 часто относят к спокойным геомагнитным условиям [Fuller-Rowell et al., 2000; Деминов и др., 2015]. Слабое отклонение геомагнитной активности для медианы foF2 зимой от спокойных условий, по-видимому, является основной причиной отсутствия значимой зависимости δfoF2 от Apm для этого сезона. Тем не менее даже для таких низких значений геомагнитной активности сохраняется общая тенденция к возникновению положительных возмущений в дневные часы зимой (см. рис. 1).

Для остальных месяцев характерно отрицательное возмущение медианы f oF2, когда увеличение Ap m приводит к уменьшению δ f oF2, значимое, по крайней мере, в полночь. Оно наиболее отчетливо для равноденственных условий, поскольку для этих условий средние значения и диапазон изменений Ap _m максимальны (см. рис. 1 и 2). Отрицательное возмущение медианы f oF2, по-видимому, обусловлено изменением температуры и состава термосферы из-за увеличения геомагнитной активности по аналогии с отрицательной фазой ионосферной бури. При прочих равных условиях такие изменения параметров термосферы летом и в равноденствия распространяются на более низкие, чем зимой, широты, обеспечивая преобладание отрицательной фазы ионосферной бури в эти периоды [Prolss, 1977; Buonsanto, 1999] .

Преобладание отрицательного возмущения медианы f oF2 во все месяцы года, за исключением зимы, приводит к тому, что и для средних за год значений δ f oF2 характерно значимое отрицательное возмущение, которое в полночь более отчетливо, чем в полдень. Амплитуда δ f oF2 12 по абсолютной величине не превышает 5–7 % в полдень и 10–13 % в полночь для анализируемых условий по данным ст. Слау (см. рис. 3). Такие слабые отклонения δ f oF2₁₂ от фона, связанные с ростом геомагнитной активности Ap 12 , по-видимому, целесообразно учитывать только при анализе эффектов в ионосфере с относительно низкой амплитудой, включая долговременные изменения или эффекты землетрясений.

ЗАКЛЮЧЕНИЕ

Предложена методика выделения вклада геомагнитной активности в медиану критической частоты F2-слоя f oF2 med . Она основана на анализе этого вклада для δ f oF2 — отношения f oF2 med / f oF2 q в процентах, где f oF2_q — критическая частота F2-слоя для спокойных условий. Величины f oF2 q и δ f oF2 зависят от солнечной и геомагнитной активности соответственно. Эти зависимости можно учесть с помощью приближенных индексов F 12 (средней за 12 месяцев величины потока солнечного радиоизлучения на длине волны 10.7 см) и Ap m (среднего за месяц значения Ap -индекса геомагнитной активности), что обеспечивает потенциальную возможность использования данной методики для прогноза f oF2 med .

С помощью этой методики по данным ст. Слау за 1954–1955 гг. для полудня и полуночи установлено, что для полуночи зависимость δfoF2 от Apm значима (при доверительном уровне 95 %) в равноденствия и летом, для полудня она менее отчетлива и значима с апреля по июль. В равноденствия и летом в полдень и полночь преобладают отрицательные возмущения δfoF2, т. е. увеличение Apm приводит к уменьшению δfoF2. Преобладание отрицательного возмущения медианы foF2 основную часть года приводит к тому, что и для среднего за год значения δfoF212 характерно значимое отрицательное возмущение, которое в полночь более отчетливо, чем в пол- день. Амплитуда δfoF212 по абсолютной величине не превышает 5–7 % в полдень и 10–13 % в полночь для анализируемых условий. Такие слабые отклонения δfoF212 от фона, связанные с ростом геомагнитной активности Ap12, по-видимому, целесообразно учитывать только при анализе эффектов в ионосфере с относительно низкой амплитудой, например долговременных изменений в ионосфере или эффектов землетрясений.

Данные foF2 ионосферной станции Слау (Slough) и индексы солнечной и геомагнитной активности были взяты с сайтов Space Physics Interactive Data Resource (SPIDR) [], World Data Center for Solar-Terrestrial Physics, Chilton [], World Data Center for Geomagnetism, Kyoto []. Работа частично поддержана Российским фондом фундаментальных исследований (гранты № 17-05-00427 и № 17-55-45094) и Программой 1.7 Президиума РАН.