Зависимость уровня смертности в регионах от распространенности активных носителей SARS-COV-2 и ресурсов организаций здравоохранения

По вопросам пандемии, порожденной SARS-CoV-2, на ресурсе E-library и некоторых других сейчас имеется очень много работ. Например, в обзоре К.В. Жмеренецкого, Е.Н. Сазоновой рассмотрены эпидемиологические и прочие особенности COVID-19, в других исследованиях изучаются и обсуждаются проблемы сбора информации о заболеваемости и смертности, достоверности статистики [1–7]. В работе О.М. Драпкиной, И.В. Самородской был сделан призыв строить математические модели прогностического типа, чему, в частности, посвящена настоящая работа [3]. В статье С. Козловского кроме аспектов учета заболеваемости и смертности рассматривается и вопрос моделирования [5].

Далее мы сфокусируемся на проблематике математического моделирования эпидемиологиче- ского процесса (ЭП), так как важность построения достаточно точной модели для COVID-19 признается многими [3, 5, 8]. На ее основе можно принимать более эффективные управленческие решения, что позволит снизить смертность, уменьшить негативные последствия эпидемии, сэкономить ресурсы. Различные подходы к построению моделей динамики ЭП описаны в обзоре М.А. Кондратьева, где рассматриваются нейронные сети, имитационное и статистическое моделирование и др. Если упростить его классификацию подходов, можно выделить два типа моделей – детерминированные и стохастические [9].

В первую очередь кратко опишем некоторые модели первого типа и их применение к COVID-19. При построении моделей, учитывающих особенности

Степанов Владимир Сергеевич – кандидат физико-математических наук, старший научный сотрудник (e-mail: , ; тел.: 8 (916) 872-52-07; ORCID: .

развития ЭП, население территории (страны, ее региона) разбивается на несколько секторов: «восприимчивые к вирусу», «инфицированные» и др. Сначала предлагается блок-схема развития ЭП во времени, в которой имеются возможные переходы индивидов из одного сектора в другой с различными интенсивностями (параметрами модели). Последние оцениваются: некоторые – по литературным данным, другие – по статистике, собранной для данной территории. Переходы между секторами блок-схемы формализуются на основе системы дифференциальных уравнений. Так, в модели Барояна – Рвачёва, позднее реализованной в системе EpidMod, используется система нелинейных интегродифференциальных уравнений в частных производных с соответствующими граничными и начальными условиями, взятая по аналогии из гидродинамики. Модели, основанные на уравнениях в частных производных функции двух переменных (времени и возраста пациента), встречаются и сейчас [10]. Однако большинство моделей развития ЭП во времени t опирается на систему обыкновенных дифференциальных уравнений первого порядка. Весьма давно была создана модель SIR, ее аббревиатура получена от английского варианта слов «восприимчивый», «инфицированный», «выздоровевший» [5, 8, 9, 11]. Позднее были разработаны ее различные модификации в виде моделей SEIR, SEIRF, SIRD и др.; в двух последних явным образом учитывается снижение числа зараженных из-за смертности: D – из-за инфекции, F – от осложнений. В библиотеке E-library с конца 1990-х гг. имеется более сотни работ с такими моделями, в основном зарубежных. Модели SIR и SEIR сейчас также широко используются при анализе динамики процессов в социальных сетях, при изучении распространения в них конкретной информации [12].

Модель SIRD применяется в работе P.V. Khrapov, A.A. Loginova к COVID-данным для РФ и ряда стран [11]. Аналогичная модель, правда, в ее конечно-разностной форме, была реализована в исследовании О.В. Друговой, Е.А. Павлова и др. для анализа динамики COVID-19 в Нижегородской области [13]. В качестве основных переменных здесь выбирались численности лиц, разбитых на четыре сектора: «риск быть зараженными» ( S ), «инфицированные» ( I ), «выздоровевшие» ( R ), «умершие» ( D ), при этом для секторов I и R предполагалось, что по 30 % лиц в них не могут быть выявлены. После подбора параметров модель подгонялась к реальным данным в начальной части роста COVID-19 в регионе, далее на ее основе выполнялся этап прогнозирования.

Модель Барояна – Рвачёва относится к виду SEIR, буква «Е» обозначает, что вводится еще один сектор «Инкубационный период» (от exposed). Он определяется временем от момента попадания инфекционной дозы вируса в организм человека до начала его заболевания COVID-19. В работе М.В. Тамма используется расширенный вариант модели SEIR, здесь также учитываются некоторые свойства терри- тории (возрастная структура населения и др.) [14]. Затем, после подбора параметров, по модели анализируется ряд сценариев борьбы с новым ЭП в Москве. В исследовании А.В. Матвеева вариант SEIR-модели, модифицированной с учетом особенностей COVID-19, был реализован в среде AnyLogic [15]. В результате для двух столичных городов сделаны сценарные расчеты, даны рекомендации по оснащению больниц инфекционными койко-местами и аппаратами для искусственной вентиляции легких (ИВЛ), сделан прогноз численности умерших.

Другой вариант модели, уже со стохастическим подходом к оцениванию, применяется в работе A. Godio, F. Pace et al. [16]. При этом используется обобщение, сделанное для ЭП исследователями L. Peng, W. Yang et al. [17]. В итоге был создан вариант SEIR-модели, в котором используется ряд параметров. Они оцениваются по данным исследования A. Godio, F. Pace et al. [16], в частности, здесь есть коэффициент смертности k ( t ) , зависящий от отсчета t и эффективности лечения пациентов. Исследователями S. Pengpeng, C. Shengli et al. [18] предложен еще один вариант SEIR-модели с учетом пониженной заразности инфицированных лиц, которые не имеют симптомов COVID-19, и с варьированием продолжительности инкубационного периода. Неизвестные параметры в исследовании находятся подгонкой модели к данным по КНР за период с 23.01 до 10.02.2020. В итоге выполнен краткосрочный прогноз и делается оценка, когда в КНР ожидается пик заражений, также приводится код программы в MATHLAB.

В работе A.V. Nikitina, I.A. Lyapunova et al. [19] рассмотрена SIR-модель и пара модификаций SEIR-модели. Предложены изменения для этих модификаций, учитывающие особенности приобретения иммунитета, а также запаздывание при выявлении зараженных лиц, исследована чувствительность. Эти результаты можно использовать при моделировании COVID-19. Также почти полвека назад в практику отечественных исследователей вошла SEIRF-модель, в Центре ИЭМ им. Н.Ф. Гамалеи к концу XX в. было создано программное обеспечение. В работах Z. Liu, P. Magal et al. и F. Ndaïrou, I. Area et al. [20, 21] эта модель применяется к данным по COVID-19, причем в последней работе она строится уже с 8-ю секторами; здесь имеется выражение для D ( t ): численность лиц, умерших за сутки t , оно включает три параметра. Отметим, что модель (1), предложенная нами ниже, может быть полезна в процессе выбора значений параметра k ( t ) в работе A. Godio, F. Pace et al. или параметров в D ( t ) [16, 21].

Кроме подхода через построение и решение системы дифференциальных уравнений имеются и более простые способы моделирования. Они используются во многих работах, посвященных прогнозированию характеристик изучаемого ЭП на основе решения обыкновенного дифференциального уравнения П. Ферхюльста и его обобщений [22–25].

Этот математик очень давно применил его для анализа роста населения в динамике по t . Оно распространено в биофизике, сейчас его используют при моделировании роста числа N ( t ) лиц, инфицированных SARS-CoV-2, по данным КНР, Швеции [22]. В этой работе рассматриваются три модели, основанные на уравнении Ферхюльста, приводятся соответствующие решения, обсуждается вопрос прогнозирования. После дифференцирования величины N ( t ) можно оценить как время наступления пика ЭП, так и количество необходимых коек в больницах согласно исследованию А.А. Куркина, О.Е. Куркиной и др. [22]. Одна из рассмотренных обобщенных моделей приводит к дифференциально-разностному уравнению. В этой модели учитывается наличие инкубационного периода в развитии ЭП, а также то, что примерно 4 % лиц, заболевших COVID-19, может погибнуть.

Модели такого типа менее чувствительны к качеству опубликованной статистики, чем перечисленные выше модели секторного типа. Они строятся по ежесуточным отсчетам временного ряда, в частности для ряда по численности умерших от COVID-19 или заболевших, и включают ряд параметров. Например, в исследовании N. Fabiano, S.N. Radenović модель Ферхюльста подгонялась к данным по численности граждан Италии, заболевших COVID-19 [23]. В другой работе эта модель была модифицирована с учетом специфики данной инфекции, что позволило при введении ряда предположений получить точное аналитическое решение [24]. Параметры этого решения были оценены на китайских данных, после чего получилось хорошее согласие модели с динамикой ЭП как для заболевших, так и для общей численности смертей в КНР [24].

Модель Ферхюльста используется также и в дискретном варианте, в котором имеется два параметра. Такой вид логистического уравнения после работ американского ученого М. Фейгенбаума стал широко использоваться при изучении различных процессов. Применительно к численности инфицированных в десятке стран и двух мегаполисах мира дискретная модель Фейгенбаума использовалась в работе Э.М. Кольцовой, Е.С. Куркиной и др., при этом ее параметры были оценены по общему числу заболевших в КНР [25]. Для Москвы здесь было рассмотрено четыре варианта роста общего числа зараженных, самый легкий из них был назван «израильским». По этому варианту к концу ЭП ожидается 300 тысяч москвичей, инфицированных SARS-CoV-2, что вполне правдоподобно согласуется с 248 тысячами на 10 августа с приростом по 700 случаев за сутки.

Наконец, в исследовании В.В. Бояринцева, Р.С. Пальмина и др. [8] выявляются закономерности развития ЭП на основе анализа общего числа I(t) инфицированных лиц, проживающих на конкретной территории. В результате при комплексе гипотез-допущений предложена рекуррентная формула расчета I(t) на t-й день ЭП. На ее основе получена зави- симость по t для функции распределения доли инфицированных лиц, затем сделаны прогнозы по странам и для Москвы.

Однако многие исследователи ЭП на основе SIR и ее модификаций, отмечают неустойчивость получаемых решений, что препятствует получению хороших прогнозов ЭП на период свыше недели [5, 8]. Также о приближенных результатах прогнозирования сообщается в исследовании А.В. Матвеева [15]. В статье С. Козловского, О. Болдырева указывается, что многие параметры для моделей ЭП, если их применять для регионов, необходимо оценивать по региональной статистике [5]. А качество ее публикаций специалисты по данным считают низким [4, 5, 7]. Экспертно ими оценивается, что уровень ее искажений растет с конца апреля 2020 г. М.В. Тамм также не доверяет статистике по смертности [5, 14]. Эталонным регионом по открытости и достоверности данных по COVID-смертности всеми признается г. Москва. По регионам ситуацию со смертностью лучше освещают Росстат и региональные органы ЗАГС. Последние на своих сайтах ежемесячно сообщают об общих случаях смерти за месяц без указания ее причин, правда, такие публикации выходят в свет с существенными задержками [4, 6, 7]. Кроме того, некоторые параметры на начальном этапе развития ЭП неизвестны; именно поэтому на этой стадии необходимо применение максимально простых моделей, содержащих минимальное количество параметров [22]. К ним можно отнести модели регрессионного анализа и временных рядов.

Если рассмотреть недетерминированные модели ЭП, в которых существующая зашумленность данных учитывается естественным образом, то в исследовании Д.В. Мелика-Гусейнова, Н.Н. Карякина и др. [26] были построены и оценены несколько регрессионных моделей для анализа COVID-смертности на уровне всей РФ. Так, модель 1 в варианте 2 имеет вид ln ( Y ) = ln ( X )·β 1 + β 0 , где Y – количество новых летальных случаев за прошедшие сутки, а X – количество новых заболеваний за эти сутки; β 0 , β 1 – параметры этой модели, подлежащие оцениванию. После подстановки оценок β 0 , β 1 из исследования Д.В. Мелика-Гусейнова, Н.Н. Карякина и др. по методу наименьших квадратов (МНК) получается линейная модель регрессии с коэффициентом детерминации R ² = 70 % [26]. Кроме того, предложена модель 2 со значением R ² = 80 %, она строится, исходя из модели 1, после введения еще одной переменной X ₂: «количество тяжелых случаев протекания COVID-19 в j -м регионе».

В работе И.А. Лакмана, А.А. Агапитова и др. предлагается достаточно сложно создаваемая модель ARIMA, а также адаптивная модель Хольта – Уинтерса – ARIMA или АРПСС – вид «авторегрессии – скользящего среднего» Бокса-Дженкинса [9, 27]. С их помощью вместе с использованием модели SIRD с высокой точностью можно сделать прогноз краткосрочной заболеваемости, смертности и выжи- ваемости COVID-пациентов на конкретной территории. Однако для SIRD-модели предполагается, что используемые коэффициенты, отвечающие за вероятности инфицирования, излечения и смерти, постоянны во времени t, что не согласуется с российской практикой. Это приводит к тому, что для получения хороших прогнозов модель приходится довольно часто перенастраивать [27].

Из-за вышеперечисленных трудностей на уровне российских регионов моделирование применяется более редко, чем на уровне стран, РФ и Москвы. Кроме того, некоторые статистические модели имеют преимущества по сравнению с секционными или логистическими моделями. Поэтому иногда сочетают оба подхода, как это было сделано в вышеуказанных работах, где вместе с SEIR-моделью применяется аналог распределения Эрланга [9, 27–29]. Среди статистических моделей весьма привлекательны модели линейной множественной регрессии [9]. Их положительными свойствами является хорошо разработанная теория, например, можно построить доверительные интервалы, вычислить коэффициенты эластичности и др. Такую модель легко реализовать при соответствующей квалификации пользователя в комплексах программ: IBM SPSS, Statistica, EViews, Deductor . Также она есть в Excel, в системах компьютерной математики MATLAB, Wolfram Mathematica и др., среде Python или R (RStudio). Наконец, здесь несложно учесть дополнительные факторы, которые могут влиять на уровень COVID-смертности. Например, добавить переменную, описывающую тяжесть протекания болезни у пациента; показатель доступности для него медицинской помощи; переменную по потреблению им табака и электронных сигарет, или другие показатели.

Необходимо также отметить, что моделированием ЭП, в частности COVID-19, сейчас занимаются известные научные центры и университеты. Например такие, как Центр моделирования инфекционных заболеваний (CMMID) из Школы гигиены и тропической медицины, Центр эпидемиологии Имперского колледжа (Лондон), университеты Женевы и Базеля, многие университеты из США и других крупных стран [5, 14]. Так, американские Центры по контролю и профилактике заболеваемости еженедельно публикуют оценки развития ЭП, полученные 24–26 группами ученых, в основном из США, для общего числа умерших от COVID-19 [30]. Эти оценки приводятся на дату t в виде точечных и интервальных прогнозов на четыре недели. Используется широкий набор моделей; так, 11 групп исследователей применяют различные виды модели SEIR (и ее стохастические варианты SEIS, SEIRD, SEIRX); пять групп – SIR-модель и ее модификацию SLIR.

Реже применяются агентные модели, нейронные сети, модели теории временных рядов и регрессионного анализа, как нелинейного, так и линейного, с применением «гребневой» оценки матрицы ковариаций (модель UM) [9, 30]. Ряд групп исследует ситуацию и на уровне штатов страны. Также некоторые иностранные эпидемиологи моделируют динамику COVID-19 в России [5, 31].

Цель исследования – построение линейной модели множественной регрессии, на основе которой можно оценивать региональный уровень смертности от COVID-19, выполнять ее точечный прогноз на ранней стадии ЭП. Также с ее помощью можно более обоснованно распоряжаться некоторыми ресурсами организаций здравоохранения в регионах России.

Материалы и методы. Модель строилась по данным о распространенности активных носителей SARS-CoV-2 в начальном периоде развития ЭП в регионе, а также с учетом показателей обеспеченности его больниц ресурсами или мощностями. Сначала была сформирована таблица «объект – признак», объектами были многомерные наблюдения (или p -мерные векторы) над n = 40 регионами РФ, исходными признаками были p = 7 показателей. Из них два изменяются ежесуточно: уровень COVID-смертности населения и соотношение числа активных носителей вируса со среднегодовой численностью жителей за 2019 г., иначе говоря, их распространенность («фактор», или «экзогенная переменная» X 1 )¹ [32]. Остальные пять брались за 2018, 2019 гг. из данных Росстата², исследования Ю. Апухтиной, С. Зобовой и данных статьи А.А. Соколова [33, 34]. Они описывали обеспечение региональных больниц: X 2 – аппаратами для ИВЛ в отделениях реанимации (2019) в расчете на 10⁵ жителей; X 3 – врачами из санитарнопротивоэпидемической группы (2018) на 10⁵ жителей; а также врачами-инфекционистами (2019), средним медперсоналом (2018), исключая сестер-акушерок; койко-местами «инфекционного типа» (2019).

Для обоснования выбора этих переменных отметим, что в некоторых исследованиях были перечислены факторы, которые влияют на летальность в ЭП [3]. Среди них оказались состояние системы здравоохранения в период, предшествующий ЭП, а также доступность и качество медицинской помощи. Переменные X2, X3… отчасти отражают это. Многие из них учитываются в процессе принятии решений за рубежом [13]. Так, в одном из университетов Германии была разработана система «Coro-naVIS» для мониторинга ресурсов госпиталей страны – их коечного фонда и аппаратов кислородной терапии [35]. После онлайн-запроса на фоне карты местности здесь сразу показывается загрузка коек и аппаратов в конкретном госпитале с его координа- тами, приводятся диаграммы загрузки в течение времени суток для близко лежащих к нему госпиталей. Это позволяет заранее избежать появления «узких мест» в процессе доставки пациентов в госпиталь, а также оптимизировать их распределение по госпиталям. В институте IHME из Вашингтонского университета разработаны модели для прогнозирования частоты случаев смерти пациентов, а также уровня занятости коек и аппаратов ИВЛ [30, 36]. В колледже из Нью-Йорка совместно с учеными из трех университетов в среде Excel создан калькулятор для оценки нагрузки, порожденной COVID-пациентами, в электронной таблице учитывается мощность больниц и загрузка аппаратов ИВЛ. В итоге здесь моделируется нагрузка на инфекционные и реанимационные отделения больниц конкретного региона, причем с учетом загрузки коек, как обычных, так и для интенсивной терапии [37].

Предварительно перечисленные выше переменные, описывающие обеспеченность инфекционных отделений больниц ресурсами (врачи-инфекционисты, медсестры, инфекционные койки), сворачивались по методу главных компонент в новую переменную. При этом использовалась небольшая модификация, предложенная ранее в работе S.A. Aivazian [38, 39]. Алгоритм расчета этой переменной, обозначенной ниже ( X ₄) ^* , включал серию шагов. Сначала каждая из переменных (показателей) отображалась на [0, 10], где 10 соответствует ее максимальному значению в таблице обучающих данных, а 0 – минимальному. Затем вычисляется оценка S ковариационной матрицы трех переменных. Далее для матрицы S находятся все ее собственные числа и векторы, один из последних задает искомые веса для расчета величины ( X 4 )^*.

Выборка объема n = 40 регионов получилась после исключения трех федеральных городов, Московской области и трех граничащих областей, а также Астраханской, Брянской, Волгоградской, Воронежской, Калининградской, Кемеровской, Мурманской, Орловской, Пензенской, Псковской, Ростовской областей; всех АО; республик Калмыкия, Коми, Марий Эл, Чувашская, многих из Северного Кавказа и некоторых других; Алтайского, Краснодарского, Ставропольского краев; еще регионов, где весной не публиковалась смертность. Статистика для многих из них критикуется в инфографике по коронавирусу в России [7].

В итоге строилась неадаптивная линейная регрессионная модель

Y = β 0 + β 1 ∙ X 1 + β 2 ∙ X 2 + β 3 ∙ X 3 + β 4 ∙( X 4 )^* + ε, (1)

где Y – уровень смертности от COVID-19;

• X 1 , …, ( X 4 )^* – четверка вышеописанных «факторов»; ε отражает влияние на Y неучтенных переменных; β 0 ,…, β 4 – неизвестные параметры, оцениваемые по выборке [9].

Величина ε в формуле (1) определяется как случайная; по определению ее математическое ожидание E(ε) = 0 и дисперсия var(ε) = σ2, причем она неизвестна. Оценки для β0,…, β4 и σ2 находятся по МНК в среде Excel по таблице с обучающими данными. Обозначим оценки β-коэффициентов через b0, …, b4. Эта таблица включала наборы значений {Y, X1, X2, X3, (X4)*} для всех n регионов, причем эти наборы входили в таблицу с разными отсчетами по t. Предполагалось, что новое число смертей М, опубликованных за сутки t для конкретного региона, является случайной величиной, приближенно имеющей биномиальное распределение, а m выявленных за сутки t активных случаев COVID-19 среди N его жителей интерпретировались как m независимых испытаний Бернулли над совокупностью из N объектов, из которых М обладают важным для нас свойством «был летальный случай» [32]. С ростом m распределение числа M приближается к пуассоновскому закону, однако вероятность смерти Pt из-за COVID-19 в регионе за сутки t точно неизвестна. Для ее оценки рассматривалась последовательность за 7–10 дней с приростами числа смертей за сутки t. Затем на основе биномиального закона строился 95%-ный доверительный интервал, и его середина бралась за оценку Pt. Далее бралось среднее значение P* этих оценок по указанной последовательности дней. Как известно, смесь пуассоновских распределений также имеет распределение Пуассона, но с другим параметром интенсивности. В итоге при формировании обучающей выборки лаг во временном ряде выбирался так, чтобы значение оценки P* вероятности COVID-смерти лежало в (3∙10–5, 9∙10–5), т.е. было менее одного летального случая на 1 млн человек. Например, Ульяновская область входит в таблицу с данными за дату 11.05.2020, а ее значение P*, рассчитанное за период 06.05–17.05.2020, равно 0,000049. Сделаем следующее:

Замечание 1 . Так как три факторные переменные X 2 , X 3 и ( X 4 )^*, описывающие обеспеченность больниц ресурсами, не изменяются (точнее, в нашем распоряжении нет данных об изменении), то выражение (1) можно записать для каждого j -го региона в виде суммы двух слагаемых. Первое – константа C ( j ), по определению равная b 0 + b 2 ∙ X 2 + b 3 ∙ X 3 + b 4 ∙( X 4 ) ^* , где X 2 , X 3 , ( X 4 ) ^* – переменные j -го региона, j= 1, …, n. Величина C ( j ) показывает, каким ожидается уровень смертности при совсем малой распространенности активных случаев в j -м регионе, когда X 1 ≈ 0. Очевидно, что чем лучше развиты ресурсы больниц в регионе, тем меньше будет значение C ( j ) . Величина C ( j ) не зависит от t , так как параметры в итоге оцениваются для (1) один раз. Второе слагаемое в (1) содержит фактор X ₁( j ), который уже зависит от t . В результате модель (1) после оценки неизвестных β 0 , …, β 4 имеет вид

Y ( j ) = C ( j ) + b 1 ∙ X 1 ( j ), (2)

где Y ( j ) – уровень COVID-смертности на 1 млн человек;

• X 1    = X 1 ( j ) – распространенность активных случаев с SARS-CoV-2 в расчете на 10⁴ жителей из j -го региона.

Индекс t здесь опущен для упрощения записи. Формулу (2) очень легко использовать для ежедневной оценки Y . Для этого надо взять в сводной таблице официального интернет-ресурса по вопросам коронавируса за дату t общие численности: инфицированных (И), умерших (У), выздоровевших (В), найти значение X 1 = 10∙[И – (В + У)]/ N , где N – численность населения из табл. 2, и затем подставить X ₁ в (2) с использованием МНК-оценки b ₁ для β 1 из (1) [32].

Замечание 2. Однако, если в i -м регионе имело место изменение одной из переменных X 2 , X 3 и ( X 4 ) ^* , и у пользователя имеется такая информация, то вместо (2) следует использовать формулу (1) с оценками b ₀, …, b ₄ вместо β₀, …, β₄ (табл. 1).

В итоге в начале июня по сформированной выше выборке были найдены МНК-оценки b 0 , …, b 4 параметров (1), равные 4,6721; 0,4494; –0,04774; –0,05668; –0,3308; оценка σ равна 0,03474. Достигнутые уровни значимости для каждого фактора и свободного члена были ниже 0,001, при расчете их через «Пакет анализа» в Excel. Оценка коэффициента детерминации R ², поправленная для отсутствия смещения, получилась выше 95 %, что, отчасти, связано с особенностью формирования обучающей выборки. Остатки для формулы (2) распределены приближенно нормально, их нормальность проверялась через d -статистику критерия, описанного Л.Н. Большевым, Н.В. Смирновым [40]. Она рассчитывается как среднее значение абсолютного отклонения, найденного по n наблюдениям для остатков в формуле (2), которое берется в соотношении с корнем из выборочной дисперсии. Эта статистика распределена примерно нормально с параметрами E ( d ), var ( d ) согласно формулам, приведенным в [40]. Численные значения для статистики критерия d и ее параметров при расчете их по остаткам (2) и выборке объема n = 40 оказались: d = 0,7954, E ( d ) = 0,8029, (v ar ( d ))^0.5 = 0,0324, поэтому гипотеза о нормальности не отвергается, так как d ≈ E ( d ), причем отклонение от E ( d ) меньше 1/4 стандарта этой статистики.

Результаты и их обсуждение. Сначала приведем табл. 1 к замечанию 2, сделанному выше. Для трех регионов здесь показан спад величины Y при росте X 2 . Отметим, что недорогой аппарат ИВЛ «Авента-M» стоит 1,8 млн руб.

Здесь вместо фактических значений по числу аппаратов ИВЛ в регионах на дату t (табл. 1) мы взяли аналогичное их количество, требуемое по нормативам, и рассчитали значение показателя X 2

для обоих случаев с учетом данных Росстата [33, 34]. Далее, подставив значение X 2 в формулу (1) и заменив предварительно здесь β 0 , …, β 4 на b 0 , …, b 4 , оценили, как с ростом значений X 2 снизился бы уровень смертности Y на момент t . Из столбца 5 и расчета по модели следует, что ожидается весьма заметное снижение Y : от 22 до 75 %.

Модель формулы (1) с оценками b 0 , …, b 4 или формула (2) может с удовлетворительной точностью ежедневно оценивать уровень смертности, порожденный COVID-19 в ряде регионов. Ниже показаны данные для 12 регионов и достигнутая для них точность по последовательности суток, взятых из промежутка по t из табл. 2. При этом ряд регионов не входил в материал обучения: Республика Карелия, Тамбовская и Курганская области. Расчеты в табл. 2 сделаны по формуле (2) с фокусом на период со второй половины мая до июля. В столбце 5 табл. 2 приводится средняя ошибка аппроксимации (MRPE):

δ= ¹⁰⁰ ⋅ ∑ ^K

K t = 1

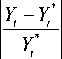
рассчитанная по модулям относительных ошибок в ходе сравнения оценки Y , полученной по формуле (2), с ее сглаженным истинным значением Y_t ^* (%). Расчет был сделан по К суткам, взятым из промежутка, который показан в столбце 4 табл. 2.

В столбце 5 табл. 2 в скобках стоит выборочное стандартное отклонение, найденное по указанной последовательности из K суток. На t -м шаге такого расчета оценка Y t по формуле (2) сравнивалась со сглаженным значением Y_t ^* (с возможной его предварительной коррекцией согласно столбцу 6 табл. 2; но если там «0», то данные [32] не изменялись). Коррекция «вверх» показателя COVID-смертности в некоторых регионах вполне оправдана, поэтому если в столбце «Примечание» указан не ноль, то это число летальных случаев, добавленных к данным [4–7, 32, 41]. В серии графиков приводится динамика этой смертности в регионах от информационного центра Минздрава в сравнении с графиками из официального ин-тернет-ресурса по вопросам коронавируса [32, 41]. Для 31 российского региона они идентичны, шесть – публикуют информацию с задержкой, 19 – иногда занижали значения относительно расследования «Медиазоны», а 29 – приводят в данные, сильно отличающиеся по многим промежуткам. Аналогичные табл. 2 значения δ можно получить и для прочих

Таблица 1

Изменение Y при улучшении обеспечения регионов аппаратами ИВЛ

Область из РФ	Наличие ИВЛ, шт.	Норматив Минздрава	Улучшение фактора X 2	Уменьшение значений Y	t
1	2	3	4	5	6
Воронежская	348	860	15 → 37	2.43 → 1.38	24.04
Тверская	118	527	9.24 → 41.3	4.7 → 3.84	26.04
Ростовская	643	1521	15.3 → 35	4.5 → 3.57	05.05

Таблица 2

Результаты расчета константы C ( j ) и средней ошибки аппроксимации δ

Регион С(j) из (2) N(j), тыс. чел.3 Промежуток по t Ошибка δ (%) из (3) Примечание Республика Карелия 1.060 620.3 06.05–05.07 5.0 (2.9) 0… +1 Республика Крым 1.163 1912.8 27.05–02.06 6.2 (2.2) 0 Республика Татарстан 2.164 3896.4 30.05– 08.07 4.5 (3.9) 0 Архангельская обл. 0.120 1149.6 02.06–09.06 3.3 (2.3) 0 Вологодская обл. 2.074 1172.2 15.05–19.05 5.2 (3.2) + 1 Курганская обл. 3.191 840.1 15.05–02.07 5.3 (3.0) + 1… +3 Липецкая обл. 1.333 1147.1 03.06–14.06 2.3 (1.6) + 1 Оренбургская обл. 0.901 1970.4 04.05 – 25.05 5.6 (2.7) 0 Рязанская обл. 1.541 1117.8 04.06–16.06 3.5 (2.0) + 4 Тамбовская обл. 1.970 1024.7 27.05–14.06 3.0 (2.3) + 2 Ульяновская обл. 1.529 1242.5 07.05–01.06 3.5 (2.2) + 1 Челябинская обл. 2.10 3484.4 18.05–27.05 1.0 (0.6) +7…0 [7] почти 30 регионов для промежутка «апрель – первая половина мая» (они входили в материал обучения с более ранними отсчетами по t).

Эта модель обеспечивает точность из столбца 5 табл. 2, пока оценка вероятности смерти P* имеет примерно те же значения, что и в материале обучения. Например, для Ульяновской области в промежутке 06.05–17.05.2020 оценка P* была 0,00049 (с учетом данных столбца 6 табл. 2), а на отрезке 18.05–02.06.2020, для дат из которого выполнялся прогноз по формуле (2), она стала около 0.0004.

Опишем чуть подробнее результаты для ряда регионов, полученные по формуле (2) на различных промежутках по t, и приведем графики на рис. 1.

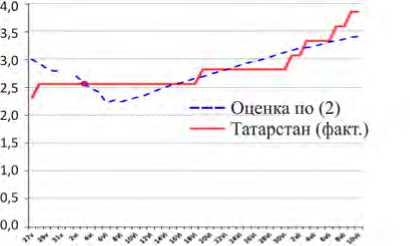
По оси ординат везде – уровень смертности в j- м регионе Y . Он находится как общее число летальных случаев в расчете на 1 млн человек. Сначала на рис. 1, а , приводятся графики для Республики Татарстан. Пунктиром показан график, построенный по формуле (2) для суток t из (27.05.2020, 10.07.2020); непрерывной линией – уровень смертности⁴ [32].

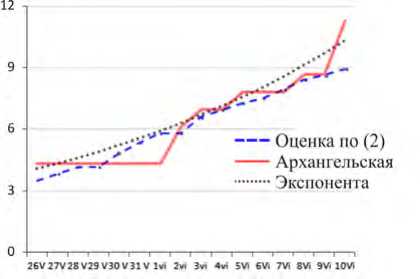
Далее на рис. 1, б , идут графики для Архангельской области⁵. Непрерывная линия показывает сглаженные данные по факту; мелкие точки лежат на экспоненте, подогнанной к Y , пунктир – согласно формуле (2) [32].

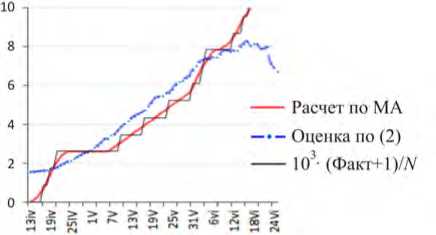
Затем представлены графики для Липецкой области (рис. 1, в ). График, показанный длинным пунктиром и точками, рассчитан по формуле (2). Значения на графике ступенчатого вида считались так: бралось число летальных случаев, далее c 17.04.2020 к ним добавлялся еще один, вероятно, еще неучтенный случай смерти, затем сумма умножалась на 10³, делилась на N ( j ) = 1147,1 (это обозначается в столбце 6 табл. 2 кодом «+1») [32]. Гладкая кривая на рис. 1, в – MA (moving average – «скользящее среднее») – рассчитана по точкам ступенчатого графика через подвижное центрированное 7-дневное окно.

в

Рис. 1. Динамика: а – для Y : Республика Татарстан; б – для Y : Архангельская обл.; в – для Y : Липецкая обл.

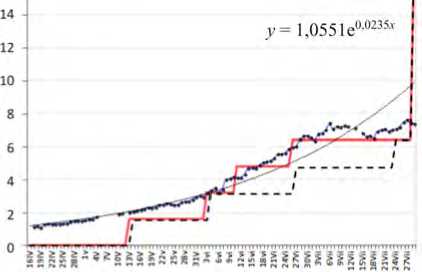
Рис. 2. Динамика показателя смертности Y в Республике Карелия и ее оценка по формуле (2)

Далее на рис. 2 приводятся графики для Республики Карелия с 16.04 по 29.07.2020. Точки темного цвета получены после подстановки значений X k в формулу (2). К этим точкам подгонялся экспоненциальный тренд, показанный тонкой линией.

Константа в его формуле есть 1,055, что соответствует почти нулевой распространенности активных случаев COVID-19, когда C(j) = 1,06 из табл. 2. Ступенчатая линия (пунктир) показывает уровень смертности, аналогичная непрерывная линия показывает Y, что была скорректирована согласно столбцу 6 табл. 2; они чуть сдвинуты, чтобы не было слияний. Начиная с 11.06.2020 при расчете скорректированной линии нами добавлялся еще один летальный случай, который, вероятно, был учтен с запозданием. Об этом дополнительном случае сообщают официальные региональные власти, это можно увидеть на репозитарии «Медиазоны» [7]. О сдвигах по t при публикации случаев смерти сообщается и в других источниках [6, 7, 26, 41]. Это предположение можно попытаться обосновать логически, анализируя уровень смертности в приграничных областях: Ленинградской, Вологодской и Архангельской. Причем его надо рассмотреть при близких значениях X1, что были в республике во вторую декаду июня (между 6,8 и 9). Из графиков на рис. 2 следует, что модель, описанная формулами (1), (2) достаточно хорошо оценивает чуть подправленный «вверх» уровень смертности на отрезке 06.06, …, 05.07.2020 (если вместо ступенчатой линии провести линию, сглаженную по скользящему среднему). Аналогичная работа была выполнена для Курганской области. Примерно похожие действия при корректировке данных о смертности проводят аналитики ряда организаций [5, 7], например в компании Data Insight, где в отделе исследований строится индекс недооценки смертности [5].

Выводы. Таким образом, построена и оценена по точности регрессионная модель, которая связывает уровень смертности в регионах с распространенностью активных случаев COVID-19, а также с обеспеченностью больниц ресурсами. Она может быть полезной в начальном периоде распространения ЭП, когда в регионе изредка наблюдаются совсем малые ежедневные приросты смертности в течение 7–10 дней, и они подчиняются распределению Пуассона. Кроме того, модель может быть полезна при построении моделей SEIR, SIRD и др. на этапе подбора параметров для них, связанных со смертностью. Также ее можно применять при распределении ресурсов организаций здравоохранения.

Финансирование. Исследование не имело спонсорской поддержки.