«Живая геометрия» как средство развития исследовательских умений студентов в условиях индивидуально-ориентированного обучения

В Государственном стандарте общего образования [8] отмечена необходимость привести результаты школьного обучения в соответствие с потребностями времени, современного общества, которое характеризуется изменчивостью, многообразием существующих в нем связей, широким внедрением информационных технологий. Важной задачей образования в этих условиях, наряду с подготовкой учащихся к решению проблем в широком круге неопределенных ситуаций, овладению информационными умениями, становится и формирование исследовательских умений.

Понятие «исследовательское умение» не является новым, идея исследовательского подхода при обучении, учения методом «искания», «открытия», появилась еще в трудах Я.А. Коменского [Коменский, 1989] и Ж.-Ж. Руссо. Исследовательские умения — это познавательные умения, обеспечивающие успешное осуществление поиска и решения проблем в различных сферах человеческой деятельности. Многие ученые (А.Е. Захарова, Ю.М. Колягин, Г.Б. Лудина, Г.В. Токмазов) к основным структурным элементам исследовательских умений относят умения: формулировать цель работы, анализировать условия заданной ситуации, выдвигать и обосновывать гипотезы, планировать решение проблемы, анализировать результат.

Очевидно, что исследовательская деятельность присутствует при изучении всех школьных дисциплин, однако при обучении математике она имеет особо важное значение. В процессе решения математических задач просто необходимы умения целенаправленно наблюдать и сравнивать, затем выдвигать и доказывать гипотезу, классифицировать изучаемые объекты, систематизировать имеющиеся знания и так далее. В таком случае правомерно поставить вопрос: «Ведется ли целенаправленная подготовка будущих учителей к формированию исследовательских умений у учащихся посредством решения математических задач?». Система курсовых и выпускных квалификационных работ закладывает основы научного исследования, но ведь очень важна привязка именно к содержанию учебного предмета и методике его преподавания. Анализ ситуации показывает, что такие исследовательские умения студенты педагогических учебных заведений приобретают лишь как один из сопутствующих результатов обучения.

Современное состояние информационных технологий в образовании открывает дополнительные возможности в формировании исследовательских умений учащихся. Посредством компьютерных программ возможно моделировать решаемые математические задачи, тем самым погружая учащихся в непосредственный процесс исследования, причем на высоком уровне самостоятельности. Основной проблемой при этом становится отбор эффективных программных средств, а также вопросы методики их применения.

Актуальность вопроса определила проблему исследования, связанную с поиском средств формирования исследовательских умений будущих учителей математики в процессе изучения геометрии в педагогическом учебном заведении.

Цель исследования заключается в обосновании возможностей компьютерной среды «Живая геометрия» как эффективного средства развития исследовательских умений студентов – будущих учителей математики в курсе геометрии.

Проблеме использования информационных технологий в преподавании математических дисциплин в средней и высшей школах посвящен целый ряд исследований (например, работы [Далингер, 2001; Майер, 2001; Марюков, 1998]. Выделяют два наиболее значимых направления использования информационных технологий: как обучающего средства и как инструмента познания. Под инструментами познания понимают активные среды, которые «поддерживают, направляют и расширяют мыслительные процессы своих пользователей» (С.Д. Дэрри), то есть не являются программами с жесткой структурой следования обучаемого [Майер, 2001].

Использование информационных технологий во многом индивидуализирует обучение, что на сегодня признается необходимым условием повышения качества образования. Проблема индивидуализации обучения активно разрабатывалась в трудах отечественных и зарубежных педагогов и психологов: И.Э. Унт [1990], И.С. Якиманской [1979] и других. А.А. Яруловым разработана индивидуально-ориентированная система обучения, ориентированная на школу [Ярулов, 2001]. Основу такой технологии составляет индивидуально-ориентированный учебный план по предмету. При организации учебного процесса учащимся предоставляется возможность выбора индивидуального маршрута освоения обязательного материала; индивидуального количества времени, затрачиваемого на изучение материала; уровня сложности материала при изучении.

В Канском педагогическом колледже технология индивидуально-ориентированного обучения была адаптирована для преподавания геометрии на математическом факультете. При разработке программы курса геометрии основные концептуальные положения индивидуально-ориентированного обучения были дополнены с учетом профессиональной направленности обучения и принципов использования информационных технологий в преподавании геометрии, сформулированных в методической системе [Майер, 2001].

В организации индивидуально-ориентированного обучения геометрии будущих учителей математики информационные технологии занимают важное место. Программные средства различного назначения используются на лекционных, практических и семинарских занятиях, а также для организации самосто- ятельной работы студентов. Одной из компьютерных программ, систематично применяемых нами на занятиях в качестве инструмента познания, является среда «Живая геометрия». Программа позволяет моделировать геометрические задачи, а значит, при определенном методическом подходе целенаправленно работать по формированию исследовательских умений студентов.

«Живая геометрия» входит в состав пакета «1С: Математика, 5–11 классы. Практикум», разработанного в рамках проекта «Информатизация системы образования», и имеется в каждой школе [1С. Образование…]. Программа позволяет получать на плоскости «живые» чертежи – модели. При этом сохраняется иерархия зависимости объектов друг от друга: изменение положения одних объектов приводит к изменению положения зависимых. Именно эта особенность и позволяет использовать «Живую геометрию» как мини-лабораторию для математических исследований.

При решении задач с использованием компьютера необходимо пройти все этапы моделирования: 1) построение информационной модели задачи; 2) построение компьютерной модели задачи; 3) проведение эксперимента; 4) анализ результатов эксперимента. Однако студенты не всегда готовы к выполнению всей цепочки процесса моделирования, поэтому в зависимости от индивидуального выбора студента можно предложить либо работу с готовой моделью (работа на 3 и 4 этапах), либо самостоятельное ее построение и только затем – исследование. При этом несложно варьировать уровень трудности заданий.

Поскольку при индивидуально-ориентированном обучении большое внимание уделяется организации самостоятельной работы студентов, то нами разработано сопровождение каждого из этапов работы по решению задач в среде «Живая геометрия». Студент вправе воспользоваться помощью, если возникают затруднения: на первом этапе – выделенные условия и требования задачи, чертеж; на втором – план построения модели в программе «Живая геометрия»; на третьем – частные случаи задачи, подлежащие исследованию; на четвертом – система вопросов, на которые необходимо найти ответы.

Использовать «Живую геометрию» полезно при решении задач на построение, при отработке теорем планиметрии, при изучении преобразований плоскости и отдельных вопросов аналитической геометрии на плоскости. Приведем несколько примеров использования среды в формировании исследовательских умений студентов.

Задача на построение треугольника по двум сторонам и медиане, проведенной к одной из них. После выполнения необходимых построений в «Живой геометрии» получается «живая» модель (рис. 1).

A b        / mb

BMC

Рис. 1

Потянув мышкой за конец одного из данных отрезков, можно наблюдать за тем, что происходит с соответствующей компьютерной моделью треугольника

АВС. Одновременно на экране можно высветить соответствующие длины не только данных отрезков, но и значения любых функций, заданных на них.

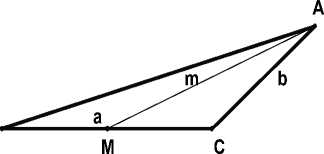
Рис. 2

Так, например, при увеличении

длины

постепенно «разворачиваться» (рис. 2), и a/2 + b треугольник выродится в отрезок. студента должна появиться гипотеза

отрезка m угол при вершине С будет при достижении медианой значения В результате такого исследования у о том, что если m ≥⋅ a/2 + b или

m <  |a/2 —b|, то задача решения не имеет. Очень важным является понимание студентом того, что это еще не доказательство. Для того чтобы подтвердить гипотезу, необходимо воспользоваться соответствующими теоремами планиметрии, в нашем случае неравенством треугольника.

Такая работа очень полезна при решении самых первых задач на построение, так как убеждает учащихся в необходимости проведения исследования.

В работе над этой задачей можно предложить следующую систему помощи:

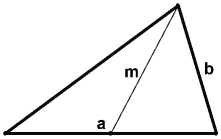
• 1)    информационная модель:

  Дано:

  a

  
  

  b

  
  

  m

  
  

  B

  
  

  A

  

  M

  
  

  C

  
  

Построить: △ АВС|, ВС=а, АС=Ь, АМ =m (АМ - медиана)

• 2)    план создания компьютерной модели, который заключается в последовательном построении на дисплее следующих простейших геометрических фигур:

• -    отрезка ВС, равного отрезку а;

• -    окружности с центром в точке С и радиусом b;

• -    точки М — середины отрезка ВС;

• -    окружности с центром в точке М и радиусом m;

• -    точки А — пересечения двух окружностей;

• -    треугольника АВС — искомой фигуры;

• 3)    проведение эксперимента по плану:

  – влияние длины отрезка а на решение задачи (при выбранных отрезках b и m);

  – влияние длины отрезка b на решение задачи (при выбранных отрезках a и m);

  – влияние длины отрезка m на решение задачи (при выбранных отрезках a и b).

• 4)    анализ результатов эксперимента:

• -    при каких ограничениях на a, b и m задача имеет решение?

• -    сколько различных решений имеет задача при каждом допустимом наборе данных отрезков?

  – при каких ограничениях на данные отрезки искомая фигура попадет в тот или иной класс треугольников (правильные, прямоугольные, тупоугольные, равнобедренные и т. д.)?

Изучение преобразований плоскости зачастую вызывает ряд трудностей, связанных и с наглядным представлением образов фигур, и с их построением. Например, чтобы представить, как изменяется фигура при аффинном преобразовании плоскости – родстве, требуется выполнять достаточно громоздкие построения, к тому же возможных вариантов очень много, и «вручную» их не охватить. «Живая геометрия» делает эту работу менее трудоемкой и более наглядной. Примером модели родства может служить построение буквы А и ее образа при родственном преобразовании, заданном осью m и парой соответственных точек T и T ^′ (рис. 3).

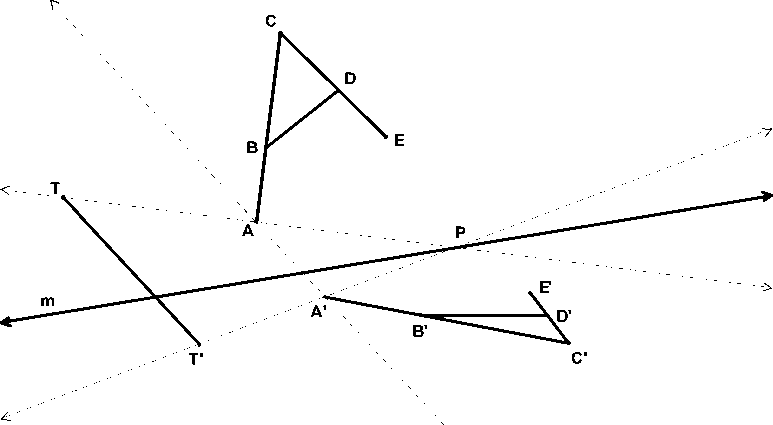
Рис. 3

Меняя положение оси родства или пары соответственных точек, можно получить все многообразие возможных образов фигуры А в родстве, один из них представлен на рис. 4.

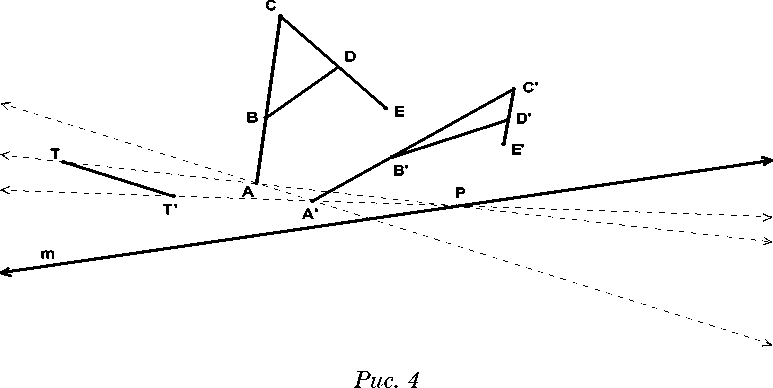
Систему помощи по исследованию этой задачи можно предложить следующую:

• 1)    информационная модель:

  – родство задается осью и парой соответственных точек;

  – прямая и ее образ в родстве пересекаются на оси родства, или ей параллельны, или совпадают;

  – прямая, проходящая через пару различных соответственных в родстве точек, отображается на себя;

  – различные прямые, проходящие через различные пары соответственных точек, параллельны между собой;

• 2)    план построения компьютерной модели:

  – прямая m, пара точек Т и Т' – произвольные;

  – точка А – любая;

  – прямая ТА;

  – точка P – точка пересечения прямых m и ТА;

  – прямая Т'P;

  – прямая l, проходящая через точку А, параллельна прямой m;

  – точка А' – точка пересечения прямых l и m;

• 3)    проведение эксперимента по плану:

  – пара соответственных точек, задающих преобразование, лежит в одной полуплоскости;

  – пара соответственных точек лежит в разных полуплоскостях;

  – направление родства параллельно оси;

  – отрезок, соединяющий пару соответственных точек, перпендикулярен оси и делится ею пополам.

• 4)    анализ результатов эксперимента:

  – от чего зависит расположение образов и прообразов в родстве?

  – что особенного в случае, когда направление родства параллельно оси?

  – какой частный случай родства дает осевую симметрию?

Опыт показывает, что у студентов на первых порах серьезные трудности вызывают этапы эксперимента и анализа его результатов. Построив модель, они не всегда могут правильно поставить цель исследования, правильно выбрать те элементы модели, изменение которых может привести к аномальным ситуациям («вырождению» модели), правильно интерпретировать увиденное на экране монитора. Только планомерная работа в этом направлении за счет компьютерной визуализации геометрической сути исследуемого и системы индивидуальной помощи позволяют выйти на высокий уровень самостоятельности студентов в решении и исследовании геометрических задач. В процессе такой работы активно развиваются исследовательские умения: формулировать проблему (умение выделять элементы задачи; строить чертеж, соответствующий тексту задачи; устанавливать связи между элементами задачи), строить компьютерную модель, планировать исследование, целенаправленно наблюдать и сравнивать, анализировать результаты, формулировать выводы.

Исследовательская деятельность должна быть посильной всем учащимся, однако уровень и скорость овладения ею у каждого свои. Индивидуальный подход здесь является одним из необходимых условий достижения нужных результатов.

Таким образом, можно сделать вывод, что специализированные математические компьютерные среды дают возможность сделать работу по формированию исследовательских умений будущих учителей математики более эффективной. Одним из таких средств является компьютерная среда «Живая геометрия», используя которую в условиях индивидуально-ориентированного обучения, можно иметь хорошие результаты: студенты лучше усваивают изучаемый материал, получают представление о сути исследования, приобретают опыт исследовательской деятельности.