Зондовые измерения в разреженной плазм

Одной из основных задач зондовой диагностики плазмы является определение концентрации плазмы, что достигается измерениями либо электронного, либо ионного тока насыщения [2]. При этом, для того чтобы измерительный зонд не влиял существенным образом на параметры исследуемого плазменного объекта, потери заряженных частиц на зонде должны быть существенно меньше суммарных потерь в плазме вследствие рекомбинации. Поэтому часто концентрация плазмы определяется по ионной ветви зондовой характеристики. Недостатком этого подхода является сложность теоретической интерпретации измеренного ионного тока.

В настоящее время для теоретической интерпретации ионной части зондовой характеристики используются различные теоретические интерпретации, применимость каждой из которых зависит от конкретных параметров плазмы (давление, температура компонент и т. п.). Так, в области низкого давления это орбитальная и радиальная теории [14], [15]. Орбитальная теория применима в том случае, когда ионы обладают значительным моментом количества движения (ионная температура отлична от нуля) и выполняется приближение бесстолкновительного движения, при этом учитываются все орбиты ионов в поле зонда. В этом случае даже редкие столкновения ионов с нейтралами разрушают орбитальное движение частиц и могут существенным образом влиять на сбор тока зондом, что показано численными расчетами методами молекулярной динамики [3].

В случаях, когда модель орбит неприменима, более корректной является теория радиального дрейфа, предполагающая чисто радиальное движение ионов на зонд. Упрощением радиальной теории является теория слоя, когда поверхность слоя пространственного заряда рассчитывается по закону «3/2», считая что весь потенциал со-

средоточен в слое, а плотность тока на слой рассчитывается по скорости kMTe (где k – постоянная Больцмана, Te – температура электронов, M – масса иона). Теория слоя дает большую ошибку при малых размерах зондов, когда отличие геометрии от плоской существенно [9]. Отметим, что как радиальная, так и орбитальная теории не учитывают ионизацию в объеме и предполагают формирование тока на бесконечности.

Теория ионного тока на электрический зонд при промежуточных давлениях без учета ионизации рассматривалась в [4], [15]. Расчеты для плотной плазмы [10] показали существенное влияние ионизации на величину ионного тока насыщения. Ввиду этого актуальным является исследование влияния ионизации на формирование ионного тока на зонд при низких и промежуточных давлениях. Учет ионизации при низких и промежуточных давлениях проводился в [8], [10]. В [8] рассматривается аналитическая модель в приближении радиального дрейфа с учетом ионизации и столкновений с атомами, в [7] допол- нительно учтены влияние температуры ионов через орбитальный момент на величину зондово- го ионного тока. Однако сравнения результатов этих работ с экспериментом не выполнялось.

В данной работе приводятся результаты некоторых экспериментов по измерению ионного тока на сферические и цилиндрические зонды в широком диапазоне размеров зондов и сравнение с моделями [1], [8].

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Для сравнения теоретических результатов с экспериментом требуется иметь хорошо изученный плазменный объект, параметры плазмы которого известным образом определяются макропараметрами разряда (родом газа наполнения, его давлением, разрядным током, размером камеры). Другой возможный подход состоит в измерении параметров плазмы (в первую очередь концентрации) независимым способом. В данной работе был выбран первый путь – зондовые измерения проводились в разреженной плазме положительного столба цилиндрической трубки. Параметры плазмы положительного столба могут быть найдены по параметрам разряда (давление, ток, размер трубки и т. д.) по известным теориям [1].

Разрядная камера, в которой зажигался тлеющий разряд, имеет форму трубки (использовались две трубки – внутренние радиусы 1,0 и 1,5 см). В трубке имеются два стеклянных отростка, изготовленных на основе вакуумных кранов, предназначенных для размещения в них зондов. Такая конструкция позволяет производить замену зондов. Расстояние между зондами составляет 12 см.

Для осуществления разряда в трубке меньшего диаметра разрядная камера была дополнена внутренней вставкой 1 (рис. 1). Диаметр внутренней трубки в эксперименте составлял 8 мм.

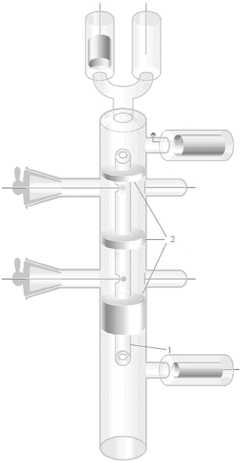
Рис. 1. Общий вид разрядной камеры с внутренней вставкой: 1 – внутренняя трубка диаметром 8 мм; 2 – перегородки

Зонды изготавливались из вольфрамовой и молибденовой проволоки. Были изготовлены сферические зонды различного диаметра (300 мкм, 500 мкм, 2,5 мм), а также цилиндрические зонды диаметрами 25 и 75 мкм. Цилиндрические зонды изготавливались методом электрохимического травления, сферические – оплавлением в электрической дуге. Для исключения подвода из эффективной площади поверхности зонда подвод в дальнейшем изолировался при помощи капилляра из молибденового стекла. Зонды посредством системы магнитного перемещения могли позиционироваться вдоль радиуса разрядной трубки.

Для откачки разрядной камеры использовался вакуумный пост Leybold PT 70 Dry, состоящий из безмасляного спирального форвакуумного насоса и турбомолекулярного насоса. Разрядная камера откачивалась до остаточного давления не выше 2 ∙ 10-5 торр. Напуск рабочего газа в камеру осуществлялся посредством натекателя. Контроль напущенного газа производился с помощью баротрона (диапазон измеряемого давления 0,05–10 мм рт. ст.). Зондовые измерения проводились по однозондовой методике. Осевое поле в разряде оценивалось по двухзондовой методике [8].

РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ

На рис. 2 представлена типичная вольт-амперная характеристика зондов, полученных в эксперименте.

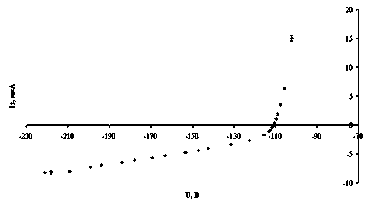
Рис. 2. Зондовая характеристика. Радиус трубки Rтр = 0,4 см; аргон 0,08 торр; ток разряда Iр = 1,5 мА; сферический зонд rз = 0,15 мм

Электронная температура T_e определялась методом первой производной зондового тока в точке плавающего потенциала, считая, что она существенно превышает производную ионного тока [7]:

id die- Г =     I*    I^- .         (1)

e \dUJ diз + dIi diз dU dU dU

Здесь I_i – ионный ток в точке плавающего потенциала, I_з – зондовый ток.

Потенциал плазмы определялся по плавающему потенциалу:

eAU     (IM

Un = U0 + AU0, -—ln ™ Ini 0,67 — I,(2)

kTe     ^

где m – масса электрона.

Ионный ток определялся по известному потенциалу плазмы путем вычитания электронно- го тока:

I = en 05 з e4

где S_з – площадь зонда.

СРАВНЕНИЕ С ТЕОРИЕЙ

Теория плазмы положительного столба в диффузионном режиме (λ _i , λ _e < R _тр ), развитая Шоттки [1], позволяет определить пара^рметры плазмы (концентрацию, частоту ионизации) по известным разрядным условиям (род газа, давление, ток).

Плотность разрядного тока связана с концентрацией электронов следующим соотношением:

j = eμ_enE ,                    (4)

где μ_e – подвижность электронов, n – концентрация электронов ( n = n_e ≈ n_p ), E – напряженность поля. Ток разряда, учитыв ^p ая бесселевский профиль концентрации, таким образом,

I = ен E J 2nrn0 Jo(2.4)dr » 0.423runоEnR^р,(5) 0              Rтр где n0 – концентрация электронов на оси. Из последнего соотношения можно получить концентрацию плазмы при известном токе разряда. Величина поля E находилась в эксперименте. В неоне μep = 1,5 ∙ 106см2 ∙ торр/(В ∙ с), в аргоне – μep = 3,3 ∙ 105 см2 ∙ торр/(В ∙ с) [6].

В пренебрежение объемной рекомбинацией частота ионизации находится из соотношения:

z = Da/Λ2 ≡ νda, Λ = Rтр / 2,4.(6)

Коэффициент амбиполярной диффузии D _a находится по соотношению:

kTe(7)

Da Ep,

e где μe – подвижность ионов. Подвижность ионов неона μpp = 4,2 см2 ∙ атм/(В ∙ с), аргона μpp = 1,53 см2 ∙ атм/(В ∙ с).

Длина свободного пробега ионов, предполагая, что доминирующим механизмом рассеяния является резонансная перезарядка, определялась по соотношению:

J = — n ^ n

.

Величины сечений σ _n для неона σ _n = 3,83 ∙ 10^-15 см², для аргона σ _n = 7,19 ∙ 10^-15 см² [12].

По известным значениям Te, n0, z, λi таким образом можно получить безразмерные параметры U = ^, a = Ik = , a = = z , i = J,, kT Jd ^0k0 kT I n 0 VkTe IM ®i ‘ J j' = en ^кте IM (^d — электронный дебаевский радиус) для сравнения с результатами теории [8], [10]. Некоторые результаты сравнения расчетных и экспериментальных ВАХ приведены на рис. 3–4.

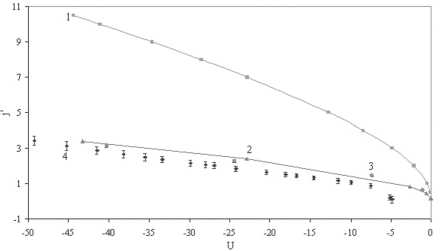
Рис. 3. Сравнение результатов эксперимента с теоретическими расчетами (неон, 0,5 торр, ток разряда 1,0 мА, радиус трубки 1 см, радиус сферического зонда 1,25 мм. 1 – радиальная теория [16], 2 – приближение радиального дрейфа с учетом ионизации и столкновений [9], 3 – учeт ионизации, столкновений и температуры ионов по [7], 4 – эксперимент. a = 2,9, l_i= 0,5, A = 0,028

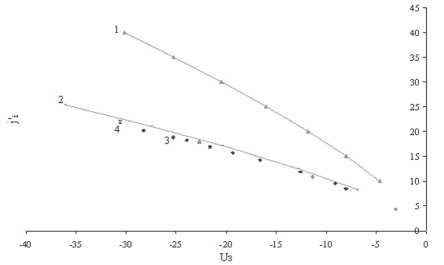
Рис. 4. Сравнение результатов эксперимента с теоретическими расчетами (аргон, 0,15 торр, ток разряда 1,0 мА, радиус трубки 0,4 см, радиус сферического зонда 0,15 мм. 1 – радиальная теория [16]; 2 – приближение радиального дрейфа с учетом ионизации и столкновений [9]; 3 – эксперимент a = 0,59, l_i= 1,1, A = 0,075, 4 – учет температуры по [7]

Во всех экспериментально исследованных случаях величина l i <  1 , вследствие чего для данных размеров зондов влияние орбитального движения пренебрежимо мало.

Результаты всех измерений для потенциала U = 20 приведены в таблице.

ЗАКЛЮЧЕНИЕ

Проведенное сравнение указывает на хорошее соответствие модели радиального дрейфа с учетом ионизации и столкновений результатам эксперимента. Значение параметра l_i ~1 и влияние ионной температуры на величину ионного тока в таких условиях пренебрежимо мало даже при размерах зондах a ~0,01 (минимальный размер в проведенных экспериментах). В то же время радиальная теория без учета ионизации и столкновений дает завышенный результат, что также связано с влиянием столкновений.

Из проведенных измерений видно, что во всех случаях результат эксперимента близок к приближению радиального дрейфа и влияние тепловой скорости ионов на величину зондового тока отсутствует. В условиях экспериментов [16] величина l_i была существенно выше (~ 50).

Сравнение результатов измерений с расчетами, U_a = -20

Зонд	Газ	Давление, торр	R , mp см	I , м ра А зр ,	Te , эВ	a	l i	A	j' (эксперимент)	j' ([16])	j' ( Ti , учет ионизации и столкновений) [9]
Сфер. Rз = 0,15 мм	Ar	0,08	0,4	1,5	3,5	0,52	1,86	0,184	17,7 ± 0,3	33,7	23
Цил. Rз = 37,5 мкм	Ar	0,08	0,4	1,5	3,5	1,3	1,86	0,184	15,6 ± 0,3	27,7	18,3
Цил. Rз = 12,5 мкм	Ar	0,08	0,4	1,5	3,5	0,43	1,86	0,184	42,0 ± 0,5	70,6	47,2
Сфер. Rз = 0,15 мм	Ar	0,15	0,4	1	2,7	0,59	1,14	0,075	16,1 ± 0,2	29,4	16,8
Цил. Rз = 37,5 мкм	Ar	0,15	0,4	1	2,7	0,15	1,14	0,075	15,0 ± 0,5	24,5	12,7
Цил. Rз = 12,5 мкм	Ar	0,15	0,4	1	2,7	0,05	1,14	0,075	44,0 ± 0,5	61,6	32,9
Сфер. Rз = 0,15 мм	Ar	0,25	0,4	1	2,8	0,74	0,86	0,037	10,4 ± 0,1	23,5	11,6
Цил. Rз = 37,5 мкм	Ar	0,25	0,4	1	2,8	0,185	0,86	0,037	10,1 ± 0,2	20,8	8,9
Цил. Rз = 12,5 мкм	Ar	0,25	0,4	1	2,8	0,062	0,86	0,037	30,0 ± 0,5	51,2	22,5
Сфер. Rз = 1,25 мм	Ne	0,5	1	1,0	3,7	2,9	0,5	0,028	1,6 ± 0,2	6,4	2,2
Сфер. Rз = 0,25 мм	Ne	0,5	1	1,0	3,7	0,58	0,5	0,028	11,0 ± 0,9	29,6	11,7
Сфер. Rз = 1,25 мм	Ne	0,23	1	1,0	5,6	1,8	0,7	0,057	3,3 ± 0,3	29,8	4,3
Сфер. Rз = 0,25 мм	Ne	0,23	1	1,0	5,6	0,37	0,7	0,057	24,0 ± 1,7	58,1	24,3
Сфер. Rз = 1,25 мм	Ar	0,08	1,5	1,5	2	2,9	1,25	0,015	3,0 ± 0,3	6,2	3,2
Сфер. Rз = 0,15 мм	Ar	0,08	1,5	1,5	2	0,35	1,25	0,015	30,0 ± 0,8	51	31
Цил. Rз = 37,5 мкм	Ar	0,08	1,5	1,5	2	0,35	1,25	0,015	20,0 ± 0,3	39	18
Цил. Rз= 12,5 мкм	Ar	0,08	1,5	1,5	2	0,03	1,25	0,015	51,0 ± 1,3	99	45
Сфер. Rз = 1,25 мм	Ar	0,15	1,5	1,0	2	2,6	0,6	0,009	2,9 ± 0,05	7,2	2,5

* Работа выполнена при поддержке Программы стратегического развития Петрозаводского государственного университета на 2012–2016 годы, Минобрнауки РФ, ФЦП «Научные и научно-педагогические кадры инновационной России (2009– 2013)», государственные контракты № 14.740.11.0895, № 14.740.11.0137, № 16.740.11.0562, № 14.740.11.1157, № 14. B37.21.0755, № 14.B37.21.0747, № 14.B37.21.1066, а также в соответствии с государственным заданием Минобрнауки России и заказом Департамента научных и научно-педагогических кадров университету на оказание услуг № 2.3282.2011 и № 2.2774.2011.