16 двухтерминных модельных схем аристотелевской силлогистики

Обстоятельством, отчасти провоцирующим написание и публикацию данной статьи, стало утверждение одних из наиболее выдающихся современных отечественных логиков В.А. Бочарова и В.И. Маркина о том, что в аристотелевской силлогистике (то есть в той силлогистике, в которой не накладываются ограничения непустоты и неуниверсальности на термины) существуют 15 возможных модельных схем, описывающих отношения между субъектом и предикатом простого категорического высказывания [1, с. 271]. Тезис данной работы состоит в том, что таких схем 16, а не 15. Для доказательства построим следующую таблицу.

Модельные схемы отношений между субъектом и предикатом простого категорического высказывания

Поясним данные схемы (схемы 1–15 представлены у Бочарова и Маркина, 16 – не представлена).

• 1.    На определенном универсуме рассуждения (предметной области) U задаются: а) непустые и неуниверсальные термины S и Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 2.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины S и Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 3.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины S и Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 4.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины Р, непустые и универсальный термин S; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 5.    На определенном универсуме рассуждения U задаются: а) непустые и неунивер-

• сальные термины S и Р; б) существуют такие элементы х, которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х, которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х, которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х, которые не обладают свойством S и не обладают свойством Р.

• 6.    На определенном универсуме рассуждения U задаются: а) непустой и неуниверсальный термин S, непустой и универсальный термин Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 7.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины S и Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 8.    На определенном универсуме рассуждения U задаются: а) непустые и универсальные термины S и Р; б) существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 9.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины S и Р; б) не существуют такие элементы х , которые обладают и свой-

• ством S, и свойством Р одновременно; в) существуют такие элементы х, которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х, которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х, которые не обладают свойством S и не обладают свойством Р.

• 10.    На определенном универсуме рассуждения U задаются: а) непустые и неуниверсальные термины S и Р; б) не существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 11.    На определенном универсуме рассуждения U задаются: а) непустой и неуниверсальный термин S, пустой термин Р; б) не существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 12.    На определенном универсуме рассуждения U задаются: а) непустой и универсальный термин S, пустой термин Р; б) не существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) не существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

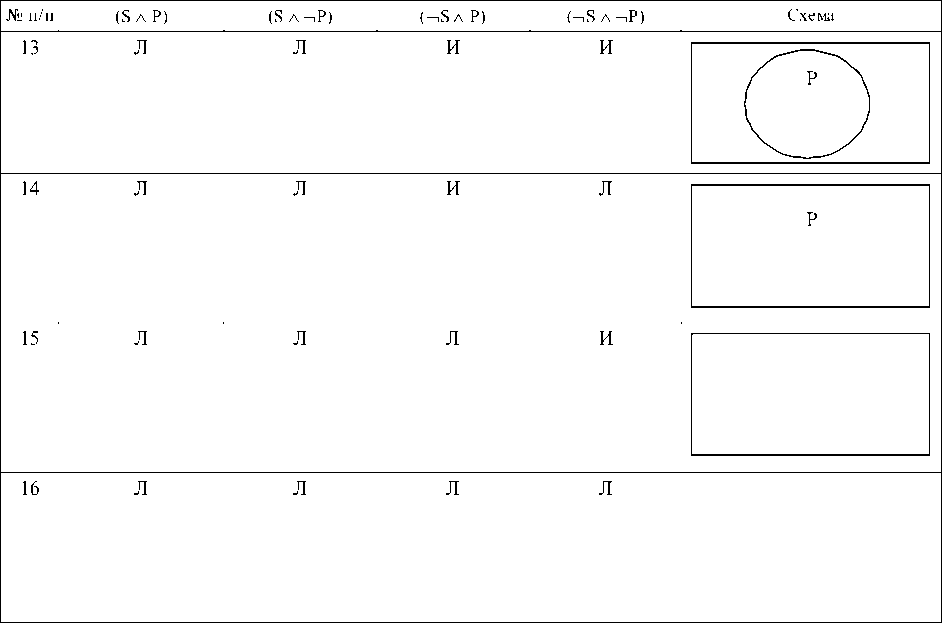
• 13.    На определенном универсуме рассуждения U задаются: а) пустой термин S, непустой и неуниверсальный термин Р; б) не существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х , которые обладают свойством S и не облада-

• ют свойством Р; г) существуют такие элементы х, которые обладают свойством Р и не обладают свойством S; д) существуют такие элементы х, которые не обладают свойством S и не обладают свойством Р.

• 14.    На определенном универсуме рассуждения U задаются: а) пустой термин S, непустой и универсальный термин Р; б) не существуют такие элементы х , которые обладают и свойством S, и свойством Р одновременно; в) не существуют такие элементы х , которые обладают свойством S и не обладают свойством Р; г) существуют такие элементы х , которые обладают свойством Р и не обладают свойством S; д) не существуют такие элементы х , которые не обладают свойством S и не обладают свойством Р.

• 15.    На определенном универсуме рассуждения U задаются: а) пустой термин S и пустой термин Р.

• 16.    Универсум рассуждения не определен (не задан), а термины S и Р являются пустыми.

Заметим, что в пояснениях к модельным схемам 1–16 утверждение (б) соответствует значению «истина» выражения (S л P), отрицание (б) – значению «ложь» данного выражения; утверждение (в) соответствует значению «истина» выражения (S л — P), отрицание (в) – значению «ложь» данного выражения; утверждение (г) соответствует значению «истина» выражения ( — 8 л P), отрицание (г) -значению «ложь» данного выражения; утверждение (д) соответствует значению «истина» выражения ( — 8 л —l P), отрицание (д) - значению «ложь» данного выражения.

Логический смысл добавления 16-й модельной схемы состоит в том, что только в этом случае можно говорить о логической полноте возможных модельных схем, описывающих отношения между субъектом и предикатом простого категорического высказывания, где 16-я схема описывает положение дел, задаваемое тождественно-ложной формулой

— (8 Л P) Л — (8 Л — P) Л — ( — 8 Л P) Л — ( — 8 Л — P).

Метафизическое обоснование данной схемы состоит в том, что система философского знания (например, система абсолютного идеализма Гегеля) может начинаться с положения дел, выражаемого категорией «ничто» (сам Гегель замечает, что вполне допустимо начать «Науку логики» не с бытия, как это представлено в его системе, а с ничто или даже с начала как такового), которую достаточно корректно можно было мыслить как отсутствие определенной предметной области, с пустыми (вследствие отсутствия предметной области) терминами S и Р какого-либо простого категорического высказывания. Заметим, что 15-я схема описывает такое положение дел, при котором задается определенная предметная область с определенными на ней пустыми терминами S и Р.