2-local derivations on algebras of matrix-valued functions on a compactum

The present paper is devoted to 2-local derivations on algebras. Recall that a. 2-local derivation is defined as follows: given an algebra A, a map A : A ^ A (not linear in general) is called a 2-local derivation if for every x, y G A, there exists a derivation Dxy : A ^ A such Л« ^A(x) = D., (x) »„! ^A(^y) = D.,^(y).

In 1997, P. Semrl introduced the notion of 2-local derivations and described 2-local derivations on the algebra B(H ) of all bounded linear operators on the infinite-dimensional separable Hilbert space H. A similar description for the finite-dimensional case appeared

later in [7]. In the paper [8] 2-local derivations have been described on matrix algebras over finite-dimensional division rings.

In [5] the authors suggested a new technique and have generalized the above mentioned results of [10] and [7] for arbitrary Hilbert spaces. Namely they considered 2-local derivations on the algebra B(H ) of all linear bounded operators on an arbitrary (no separability is assumed) Hilbert space H and proved that every 2-local derivation on B(H ) is a derivation. After it is also published a number of papers devoted to 2-local derivations on associative algebras.

In the present paper we also suggest another technique and apply to various associative algebras of infinite dimensional matrix-valued functions on a compactum. As a result we will have that every 2-local derivation on such an algebra is a derivation. As the main result of the paper it is established that every 2-local derivation on a *-algebra C(Q,M _n (F )) or C (Q, N _n (F )), where Q is a compactum, M _n (F ) is the *-algebra of infinite dimensional matrices over complex numbers (real numbers or quaternoins) defined in Section 1, N _n (F ) is the *-subalgebra of M _n (F ) defined in Section 2, is a derivation. Also we explain that the method developed in the paper can be applied to Jordan and Lie algebras of infinite dimensional matrix-valued functions on a compactum.

We conclude that there are a number of various associative algebras of infinite dimensional matrix-valued functions on a compactum every 2-local derivation of which is a derivation. The main results of this paper are new. The method of proving of these results presented in this paper is universal and can be applied to associative, Lie and Jordan algebras. Its respective modification allows to prove similar problem for Jordan and Lie algebras of infinite dimensional matrix-valued functions on a compactum. In this sense our method is useful.

1.    Preliminaries

Let M be an associative algebra.

Definition. A linear map D : M ^ M is called a derivation, if D(xy) = D(x)y + xD(y) lor every two elements x,y E M.

A map A : M ^ M is called a 2-local derivation, if lor every two elements x,y E M there exists a derivation D _x,_y : M ^ M such that A(x) = D _x,_y (x), A(y) = D _x,_y (y).

It is known that each derivation D on a von Neumann algebra M is an inner derivation, that is there exists an element a E M such that

D(x) = ax — xa, x E M.

Therefore for a von Neumann algebra M the above definition is equivalent to the following one: A map A : M ^ M is called a 2-local derivation, if lor every two elements x,y E M there exists an element a E M such that A(x) = ax — xa. A(y) = ay — ya.

Let throughout the paper n be an arbitrary infillite cardinal number. E be a set of indices of the cardinality n. Let {e ij } be a set of ma tri.c units such that e ij is a n x n-diinensional matrix, i. e. e ij = (a^ae ) _ав е г- tlie (i,j )-tli component of which is 1. i. e. a j = 1. and the rest components are zeros.

Let {m^} Ise a set of n x n-dirnensional matrixes and m ^ = (m ^ ) _ав е г for every £. Then by P- m ^ we denote the matrix whose components are sums of the corresponding components of matrixes of the set {m ^ }. i. e.

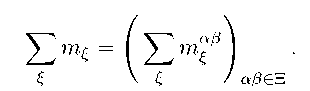
ξ mξαβ

ξ        αβ ∈

Here, the maximal quantity of nonzero summands of the sum P, m^ is countable.

Let throughout the paper F is the held of complex numbers C (real numbers R or quaternion body H) and

Mn(F) =

{x

i,jG=

Xij e ij : (V i,j : X ij E F )(3 K E R)

(V n E N)(V { eki } nl₌₁ C {e ij })

n

λklekl kl=1

6 K ,

where | £^=1 ^Xkleki^ the norm of the matrix £^=1 ^Xkleki in the finite dimensional C *-algebra, generated by {e _kl }^T n_l= ₁. It is easy to see that M n (F ) is a vector space over F.

In Mn(F) we introduce an associative multiplication as follows: if x = E Xij eij-, y =        eij are elements of Mn(F) then

ХУ = X [X ^    eij- .

With respect to this operation M n (F ) becomes an associative algebra and M n (F ) = B(l₂(S)), where l₂(5) is a Hilbert space over F with elements {xi}_ie=. xi E F lor all i E 5. B(l₂(S)) is the associative algebra of all bounded linear operators on the Hilbert space l₂(S). Then M n (F ) is a von Neumann algebra of infinite n x ndimeiisional matrices over F if F = C (see [2]) and M n (F ) is a real von Netunarm algebra if F = R or H.

Recall that a Hilbert space H is an infinite dimensional inner product space which is a complete metric space with respect to the metric generated by the inner product [1, Section 1.5]

Similarly, if we take the algebra B(H ) of all bounded linear operators on an arbitrary Hilbert space H and if {q i } is an arbitrary maximal orthogonal set of minimal projections of B(H r th ™B (H ) = P _{4 i} B^(H j^yy

Let throughout the paper X be a hyperstonean compactum, C (X) denote the algebra of all F-valued continuous functions on X and

M = X Xij(x)ej : ( V i,j : X ij (x) E C (X) )( 3 K E R ) i,j e S

(V m E N) ^}m=i C{e ij })

E  Xkl(x)eki kl=1,...,m

6 K ,

where ^ P_kl=_1v..,_m X^kl(x)eki || is the norm of P_kl=_1v..,_m X ^kl (x)e_M in the C *-algebra C (X, M_n(C)), where M_n(C) the finite dimensional C *-algebra, generated by {e _kl 7^ =1. It is clear that M_n(C) = M_n (C) and

C (X,M n (C)) = C (X) 0 Mn(C).

The set M is a д-ector space with point-wise algebraic operations. The map k • k : M ^ R₊ defined as

n

X ^kl ( x ) e kl kl =1

kak = sup {ekl}ni=1C{eij } is a norm on the vector space M, where a G M a nd a = ^KijG5 Aij (x)eij. In M we introduce an associative multiplication as follows: if x = 52 Aij (x)eij, У = 52 ^3 (x')eij are elements of M then xy =EEAi^(x)^j(x)ej G M. i,j∈Ξ ξ

With respect to this multiplication M becomes an associative algebra and M is a real or complex von Neumann algebra of type I_n by Theorem 5 in [4].

Let M be a C *-algebra. A : M ^ M be a 2-local derivation. Now let us show that A is homogeneous. Indeed, lor each x G M. and lor A G C there exists a derivation D _x,_Ax such that A(x) = D_x, _Ax(x) and A(Ax) = D x,\x (AxY Then

A(Ax) = Dx,Ax(Ax) = ADx, Ax(x) = AA(x).

Hence, A is homogeneous. At the same time, for each x G M, there exists a derivation D _x,_x 2 such that A(x) = D _xx (x) and A(x²) = D _xx (x²). Then

A (x²) = D xx (x²) = D xx (x)x + xD_x,_x2 (x) = A(x)x + xA(x).

In [6] it is proved that every Jordan derivation on a semi-prime algebra is a derivation. Since M is semi-prime (i. e. aMa = {0} implies that a = {0}). the map A is a derivation if it is additive. Therefore, to prove that the 2-local derivation A : M ^ M is a derivation it is sufficient to prove that A : M ^ M is additive in the proof of Theorem 1.

2.    2-local derivations on some associative algebras of matrix-valued functions

Let Q be a compactum. Then the algebra C (Q) of all continuous complex number-valued functions on Q is a C *-algebra and by Theorem 1.17.2 in [9] the second dual space C (Q)** is a commutative von Neumann algebra. Hence there exists a hyperstonean compactum X such that C (Q)** = C (X). If we take the *-algebra C (Q,M_n(C)) of all continuous maps of Q to M_n(C). then we mar - assume that C (Q,M_n(C)) C M. In tins ctise the set {e ij } of constant functions belongs to C(Q,M _n (C~)~) and the weaк closure of C(Q,M _n (C~)~) in M coincides with M. Hence by separately weakly continuity of multiplication every derivation of C(Q,M _n (C)) has a unique exteushm. to a derivation on M [9. Lemma 4.1.4]. Therefore, if A is a 2-local clerivation on C (Q, M_n (C)). then for even - two elements x. y G C (Q,M_n(C)) there exists a derivation D _xy : M ^ M such that A(x) = D _xy (x), A(y) = D _xy (y), i. e. D _xy is a derivation of M (not оnly of C (Q, M n (C))). The following theorem is the key result of this section.

Theorem 1. Let A be a 2-local derivation on C (Q,M_n(C)). Then A is a derivation.

We first prove some lemmas necessary for the proof of Theorem 1.

By the above arguments for every 2-local derivation A оn C(Q,M _n (F)) and for each x G C(Q,M n (F )) there exist a G M such that

A(x) = ax — xa.

Put eij := E ^ne ^, ^,пег where for all € n- if € = in = j tlien A^n = 1 otherwise A^n = 0. aiid 1 is unit of the algebra C(Q). Let {a(ij)} C M be a subset such that

A(eij) = a(ij)eij - eija(ij').

for all i. j. let a^ijeij, a^ij E C (Q) be the (i, j)-th component of the element eii a(ji)ejj ( >f M for all pairs of different indices i, j and let P^=_n a⁵ⁿe^_n be the matrix with all such components, the diagonal components of which are zeros.

Lemma 1. For each pair i, j of different indices the following equality is valid

^{4 (e} ij ) — ^ ^ a П e ^n ^e ij    ^e ij ^ ^ a П e ^n + ^a(ij"⁾ ii ^e ij    ^e ij ^a(ij ) jj ,              (!)

C Let k be an arbitrary index different from i. j and let a(ij,ik) E M be an element such that

A(e ik ) = a(ij, ik)e ik - e ik a(ij, ik) and A(e j ) = a(ij, ik)e j - e ij a(ij, ik).

Then ekkA(eij)ejj = ekk Q^iijiki'eejj - eija(ij,ik) ejj = ekka(ij,ik)ej - 0

— ^e kk ^a(ik)e ij    e kk e ij ^ ^ a n e ^n ^e jj — ^e kk ^a ki ^e ij

-

ekk eij     a η eξη ejj f=n

S=n

• —    ^e kk     a П e ^n e ij    e kk ^e ij     ^a^Пe^n ^e jj — ^e kk I     ^a^Пe^n ^e ij    ^e ij     ^a^П e ^n   ^e jj •

f = n                   f = n                 V f = n                f = n /

Similarly, ekk A(eij )eii — ekk I ^ a^ne^neij   eij ^ a^negq I eii.

\^=n                ^=n       /

Let a(ij,kj) E M be ап element such that

A(e kj ) = a(ij, kj)e _kj - e kj a(ij, kj )  and   A(e ij ) = a(ij, kj)e ij - e ij a(ij, kj )•

Then en A(eij)ekk = en (a(ij, kj)eij - eija(ij, kj) ekk

= 0 - e ij a(ij, kj)e kk = 0 - e ij a(kj)e kk = 0 - e ij a jk e kk

• —    ^e ii      a n e ^n ^e ij ^e kk    ^e ij     ^a^n e ^n ^e kk — ^e ii I       ^a^n e ^n ^e ij    ^e ij     ^a^n e ^n   ^e kk •

^=n                 ^=n               ^<^              ^=n      /

Also similarly we have ejjA(eij)ekk = ejj I ^ ane^neij   eij ^ a^ne^n I ekk,

\^=n                ^=n       / eξη  eii ,

eii ^A(e ij ^)e ii — ^e ii I      a^e^n e ij    e ij    у a^¹

VS=n                S=n ejjA(eij)ejj — ejj I 52 a^neEneij eij 52 a^' \^=n                ^=n eξη ejj .

Hence the equality (1) is valid. B

We take elements of the sets {{eis}-}i and {{e^j}-}j in pairs ({e_a^}-, {e^sn.) such that а — в- Then using the set {({e_a^}-, {e^sn.)} °f such pairs we get the set {e _ae }.

Let x o — {e _ae } be a set {v ^ij e ij } ij such thsit for all i. j if (а, в ) — (i, j) then vij — 0 E C(Q) else vij — 1 E C (Q). T1 ien xo E C (Q,M _n (C)). Fix differ ent indices io. jo. Let c E M be an element such that

A(,. , .. ) — ce iojo - e iojo c ^arld A(x_o) — cx o - X o C.

Put c — Pij^ c^ij eij E M a nd a — Pi=j a^ij eij + P_iG5 aii en, where aiieii — cii eii for every i E E.

Lemma 2. Let ^, n be arbitrary different indices, and let b — 52_ij_G= b^ijeij E M be an element such that

A(e ^_n ) — beEn — e^_nb ^ajK^ A(x_o) — bx o - x o b.

Then c^ - cⁿⁿ — b^S - bⁿⁿ.

C We have that there exist а, в such that e ^_a ,e e_n E {e _ae } (or e_an, e^ E {e _ae }, or e _a p E {e _ae }), and there exists a chain of pairs of indices (dt , fd) in H, where Q — {((d,/3) : e &,p E {e ae }}- connecting pairs (£,а), (в,п), h e.

⁽ ^^{,а )} , ^{( а}, €1), ⁽ €r,nr)> •••, ⁽ П2^,в), ^{( в,}П ⁾ -

Then c€€ - caa — bSS - baa   caa - cCi€1 — baa - b^iEi ciiD - cnini — b^iEi - bnini    ...    cn2n2 _ cee — ьП2П2 _ bee    c№ - cnn — b/3/з _ bnn.

Hence c€€ _ b€€ — caa _ baa   caa _ baa — c^i^i _ b^i^i cSi^i _ b^idi — cnini _ bnini    ...    cn2n2 _ bn2n2 — cee _ bee    cee _ bee — cnn _ bnn.

and c^SS - b^SS — cⁿⁿ - b ⁿⁿ. c ^SS - cⁿⁿ — b^SS - b ⁿⁿ.

Therefore c ^SS - cⁿⁿ — b ^SS - b ⁿⁿ. B

Lemma 3. Let x be an element of the algebra C(Q , M_n(C)). Then

A(x) — ax - xa, where a is defined as afjove.

C Let d(ij ) E M be an element such that

A(e ij ) — d(ij)e ij - e ij d(ij ) and A(x) — d(ij)x - xd(ij')

and i = j. Then

A(eij) = d(ij)eij — eij d(ij) = eiid(ij )eij — eij d(ij)ejj + (1 — eii)d(ij)eij — eij d(ij )(1 — ejj) — a(ij)iieij   eija(ij)jj + 5 у a^’eEneij   eij 5 v 0’eEn s=n                i=n for all i. j Irv Lemma, 1.

Since eiid(ij )eij    eij d(ij^ejj — a(ij )ii eij    eij a(ij )jj we have

(1 — en)d(ij)en = 52 ^a^e ^n e ii ,  e jj d(ij)(1 — e jj ) = e jj 52 a^€n e^

^=n                                      ^=n lor all different i and j.

Let b = Pij_GS b ^ij e ij E M be an element such that

A(e ij ) = be ij — e ij b arid A(x o ) = bx o — x o b.

Then b ii — b j^j = cii — c ^jj Irv Lemma 2. AVe har'e b ii

-

b ^jj = d(ij')' ¹'¹ — d(ij) ^jj since

be ij — e ij b = d(ij )e ij

— e ij d(ij').

Hence

C ii — c i^j = d(ij) i'ⁱ — d(ij) ^jj ,   c ^jj

-

cii = d(ij ) jj — d(ij ) ii .

Therefore we have ejj A(x)eii = ejj (d(ij )x — xd(ij ))ea

= e jj d(ij)(1 — e jj )xen + e jj d(ij )e jj xe ii — e jj x(1 — e ii )d(ij)e ii

-

e jj xe ii d^ij^e ii

— ^e jj 5 у a^ П ^e ^n ^xe ii №n

-

e jj x 52 a^ⁿ e ^n e ii + e jj d(ij)e jj xe ii E=n

-

e jj xe ii d(ij )e ii

= e jj 52 a^?ne^n xe ii №n

-

e jj x 52 a ⁵ⁿ e ^n e ii + c jj e jj xe ii S=n

-

e jj xe ii c e ii

= e jj 52 a^ⁿ e ^n xe ii S=n

-

e jj x 52 a^ⁿ e ^n e ii + e jj &n

e ξξ xe ii

-

e jj x

e ξξ e ii

= e jj 52 a^ⁿe?n xe ii S,n E 5

-

e jj x 52 a^ⁿe? _n e ii = e jj (ax — xa)e _ii . §,nG5

Let d(ii), v,w E M be elements such that

A( e ii ) = d ( ii ) e ii — e ii d ( ii )

and A(x) = d(ii)x — xd(ii),

A(en ) = ven

-

e ii v,

A(e ij ) = ve ij —

e ij v,

A(en ) = wen

-

e ii w,

A(e ji ) = we ji

-

^e ji ^w.

Then we deduce

(1 — eii )a(ij)en = (1 — eii )ven = (1 — eii)d(ii)eii, en a(ji)(1 — en) = eii w(1 — eii) = end(ii)(1 — en).

By Lemma 1

A(e ij ) = a(ij)e ij - e ij a(ij) =     a ⁵ⁿ e ^n e ij - e ij У^ a ⁵ⁿ e ^n + a(ij) ii e ij - e ij a(ij) ^jj

S=n                i=n and

(1 - en)a(ij)en = ^a^e^en- S=n

Similarly ena(ji)(1 — en) = en ’^O^’1 e^■ S=n

Taking all this into account, we derive the following chain of equalities:

e ii A(x)e ii = en (d(ii)x

-

xd(ii))e ii

= end(ii)(1

= e^a ji)(1

-

-

en)xen + e ii d(ii)en xe ii e ii )xe ii + e ii d(ii) en xe ii

-

-

enx(1

enx(1

-

-

en )d(ii)e ii en )a(j)en

-

-

e ii xe ii d(ii)e ii e ii xe ii d(ii)e ii

= en У2 a ^?n e ^n xe ii №n

-

enx     a ⁵ⁿ e ^n e ii + e ii d(ii) e ii xe ii

E=n

-

e ii xe ii d(ii)e ii

= en У^ a ⁵ⁿ e ^n xe ii S=n

-

^e ii ^{x    a}^ e ^n ^e ii ^{+ c e} ii ^xe ii

^=n

-

e ii xc e ii

= en У^ a ⁵ⁿ e ^n xe ii S=n

-

^e ii ^x     a^П e ^n e ii ⁺ e ii

^ = n

e ξξ xe ii

-

^e ii ^x

^e ξξ ^e ii

= en У2 a ^ ⁿ e ^n xe ii S,n E 5

-

e_tix У^ a ⁵ⁿ e ^n en = en (ax - xa)en. ^,n e a

It follows that

A(x) = aax - xaa

lor all x E C(Q,M _n (C)y B Proof of Theorem 1.

By Lemma 3 A(e _ii ) = ae ii

-

e ii a E M. Hence

a ^ξi e ξi -     a ^iξ e iξ ∈ M.

ξξ

Then and

^e ii

^e ξi

-

£ a i^ e ij = a ii e ii - £a i« e i^ E M ξξ

^e ξi

-

_a iξ _{e iξ} ξ

en = ^a ^ e .i ξ

- a ⁱⁱ e ii ∈ M .

Therefore. P^ a^ie^i. P^ ai^ ei^ E M. i- e. aen,en a E M- He nee en ax,xaen E M lor each i. Let

V = |.E A ^j e ii : <^A ‘jj c CX )}.

Then ax,xa G V for each element x = {x ij e ij } 6 C (Q, M_n(C)), i. e.

X a i ⁵x ^j e ij , X x i ⁵ a⁵e ij G C(Q')^

ξξ for all i, j. Thus, for all x,y G C(Q, Mn(C)) we have that the elements ax, xa, ay, ya, a(x+y), (x + y)a beloiig to V. Hence

A(x + y) = A(x) + A(y)

by Lemma 3.

Similarly lor all x. y G C(Q, M n (C)) we have

(ax + xa)y = axy — xay G M, axy = a(xy) G V.

Then xay = axy — (ax — xa)y and xay G V. Therefore

a(xy) — (xy)a = axy — xay + xay — xya = (ax — xa)y + x(ay — ya).

Now it can be easily seen that

A(xy) = A(x)y + xA(y)

by Lemma 3. By Section 1 A is homogeneous. Hence, A is a linear operator and a derivation. The proof is complete. B

If we take the *-algebra C(Q,M_n(F )), F = R or H, then we can similarly prove the following theorem.

Theorem 2. Let A be a 2-local derivation on C(Q,M_n(F )). Then A is a derivation.

To prove Theorem 2, we need to repeat the proof of Theorem 1 with very minor modification.

Let P T Fe ij be the following set

| X X i e ij : (V i,j

X ij G F) (V E > 0) (3 n o G N)

(V n > m > n o )

X X   (Xkieki + Xikeik) + Xiieii   

where k • k is a norm of a inatrix. Then jF Feij c M_n(F)-

Theorem 3. ^Oj Feij is a C*-algebra with respect to the algebraic operations and the norm in M_n(F) (see [3]).

C We have POj Feij is a normed subspace of the algebra M_n(F).

Let (an) be a sequence of elements in Pj Feij such that (an) norm converges to some element a G Mn(F). We have eiianejj ^ eiiaejj at n ^ to lor all i and j. Hence eiiaejj G eiiMn(F)ejj lor all i. j. Let and

ⁿ c_m

b

n

∞i

= E E(ei-i i=n k=1

1^aekk^{+ e}kk ^aei-1,i-1^{) + e}ii^aeii

]

∞

X i=n

i

k=1

(ei-1,i-

1 amekk + ekk am ei—1,i—1) + e^ameii

for any n. Then cm ^ bn as m ^ to. It should be proven that (bn) is a fundamental sequence. Let e E R₊ and fix n. Then there exist mo such tinit for all m > mo

Ibn - cmil < e.

Hence for every no > n and m > mo

∞

=П0 ekk) ^ -

∞

E k=no

^ekk

= ^bn⁰

- cm || < |-

At the same time, since am E jW Feij, there exists n1 > no such that for all l > p > n1 we

\\4 - cm II < |.

Therefore lor all l > p > n1 the following relations hold:

• 11 bl - bp 11 = 11 bl - ^cm ^{+ c}m - cm ⁺cm - bp I I

61¹ bl - cm 1¹ +1¹ cm - cm 1¹ +1¹ cm - bp 1¹< 3 + 3 + 3=¹

Since e is arbitrarily chosen, (bn) is fundament al. Therefore a E Pj e_iiM_n(F)ejj. Since the sequence (an) is arbitral'ily chosen. Pj Feij is a Banach space.

Let Pi,j_EE aij, Pi,jES bij^be arbitrary elements of the Banach space PT Feij. Let am = Pm)₌₁akl- bm = ^pkz₌₁bkl^{for ab natural} numbers m. We have tlie sequence (am) converges to P_i,j_E= aij and the sequence (b_m) converges to Pi,j_EHbij hi Pj Feij. Also for all n and m ambn E Pj Feij. Then lor any n the se<равнее (ambn) convex'ges to Pij_E= aijbn as m ^ to. He nee P_jE5aij bn E Pj Feij. Note that Pj Feij C Mn(F). Therefore, lor any e E R₊ there exists п_о such that

E aij bn+i - E i,jEE             i,jEE

aij bn

aij i,jEE

¹¹bn+1^-bn¹¹ 6 ^e

lor any n > п_о. Hence the sequence ({aij}bn⁾ com-ei'ges to ip^a, aij ]Ni j_Es bij ^asn ^ to. Since Pj enMn(F )вц is a Bana ch space. Pij_E= aij Pij_E= bij E Pj Feij. Now. the relation P^jFeij C Mn(F). implies that P^jFeij is a C^-algebraS

Since Feii is a simple C'-algebra for all i, the proof of Theorem 8 in implies that [3] the

C*-algebra Pj Feij is simple.

Let Nn^(F) = Pjj Feij Tltei. C(Q, Nn^(F)) ie - real..r complex C'-algebra.. where IF = C. R or H) a nd C (Q, Nn(F)) C M. Hence similar to Theorems 1, 2 we can prove the following theorem.

Theorem 4. Let A be a 2-local derivation on C(Q, Nn(F)). Then A is a derivation.

It is known that the set Msa of all self-adjoint elements (i. e. a* = a) (if M forms a Jordan algebra with respect to the multiplication a • b = 2(ab + ba). The following problem can be similarly solved.

Problem 1: Develop a. Jordan analog of the method applied in the proof of Theorem 1 and prove that every 2-local derivation A on the Jord an algebra M_sa о r C (Q,M_n(F)_sa) or C(Q, N_n(F)_sa) is a derivation.

It is known that the set M_k= {a E M : a* = -a} forms a Lie algebra with respect to the multiplication [a, b] = ab - ba. So it is natural to consider the following problem.

Problem 2: Develop a Lie analog of the method applied in the proof of Theorem 1 and prove that every 2-local derivation A on the Lie algebra M_k оr C(Q,Mn(F)_k) or C(Q, Nn(F)k) is a derivation.

The authors thank К. K. Kudaybergenov for many stimulating conversations on the subject.