A community based reliable trusted framework for collaborative filtering

Published Online February 2019 in MECS

The magnitude of information growing on Web 2.0 sources a severe problem known as information overload because of which users face difficulty to find the trustworthy information or a relevant item. Recommender systems act like an agent which helps users to purchase right items or to find precise information in an information overload environment.

These systems can also be merged with social networking tools to provide dynamic collaborative communication which is often known as web personalization[1]. It is a process of organising the structure of a website to fulfil the specific interests of user’s navigational behavior which can be done using two common techniques such as, content and collaborative recommenders. The framework of the content-based approaches utilizes a series of distinct features of an item in order to recommend supplementary items with similar properties. These approaches represents the data as features. This representation needs support of human editors for non-machine parsable items which is very time consuming, expensive and error-prone activity. Such a system is almost impossible to classify and to provide desired features for the items like jokes.

On the other hand Collaborative Filtering (CF) systems gather the interests/opinions from the users in terms of ratings and provide recommendations based on interests. The system identifies users with similar interests and provides suggestions for non-rated items adored by them in the past. The collaborative recommender system can be functional on any kind of items such as, movies, songs, books, news, songs and websites. This system can also scale well to large items since these methods do not entail any human support. Collaborative Filtering systems are again classified into two: one is user-based (UBCF) and the other is item-based(IBCF). In the userbased method, identify k-similar closest neighbors for the target user on the base of user by user similarity matrix. Afterwards, prediction process for the unrated items is performed. However this approach suffers with sparsity and scalability problems. Item-based approach reduces the scalability issue by considering the correlations among items. But it still performs poor in resolving the issues of new items and sparsity.

To address the issues faced by CF systems, many solutions were suggested. Web personalization merging with item-based collaborative approach is one such method in order to progress the eminence of predictions and to reduce the neighborhood [2]. In other alternative approach, a similarity matrix is computed using the distance between the use of retrieval and the ratings. Retrieved documents and terms were explored using transitive relations from the word graph in order to progress the worth of information retrieval. In another approach Co-ratings between users were considered as edges to build a graph of interactions to recommend items to authors based on his/her target items’ group. Group recommendations gain more popularity than individuals’ personalization due to the inclusion of social relationships as activities in social networks incline to be in groups. Community detection approaches to extract group friendship relations was the recent trend which tremendously reduces the size of neighboring.

The community-based collaborative approach follows three steps: Firstly, it identifies the community of the target item (highest rated item) for every user. Thereafter, it performs Pearson correlation coefficient to calculate a similarity value between items. This correlation works based on the common ratings given by the users since similar taste share similar interest. Secondly, the predictions for the candidate items are computed based on the common user’s items ratings that belong to the community of the target item. Finally the top predicted items are suggested to the user [3, 4].

Many algorithms were addressed to overcome the problems of scalability, cold-start and quality of recommendations. In reality, people always turn to friends for suggestions by incorporating trust into consideration to accomplish group recommendations. The malicious/unreliable user may favor unwanted items and unfavour wanted items by giving highest predictions which reduces the reputation and accuracy of recommender systems [5]. To prevent this, fortunately online social media and social networks have made it easy for users to indicate whom they trust and whom they do not. Furthermore, the ratings data is sparse but item/user similarity is assessable only on these sparse ratings. Hence, the number of prospective neighbors are highly reduced. Therefore, the methods to reduce the neighborhood minimization became popular in recent days. Community-based and Trust-based collaborative filtering belongs to such approaches. The proposed approach combines community as well as a trust to alleviate cold start, sparseness and to ignore malicious users from trust propagation.

The paper is structured as follows: Background works are revised in section II and section III presents the proposed approach. We illustrated the approach with an example in section IV. In section V, we confirmed the effectiveness of the present approach on MovieLens dataset; and finally outlined conclusions in section VI.

• II.    Related Work

Community-based recommender approaches have appealed much research attention. Discovering communities allow us to decrease sparsity and attention on observing the hidden features of communities instead of individuals. Many algorithms were proposed to detect communities based on social features and dynamic attention. A recent trend is on the amalgamation of community detection and recommender systems to afford personalized recommendations to users belonging to the same community. In fact, users within a community share similar interests (or preferences).

Comprising social issues or trust declarations in the recommender system lead to rise in the accuracy of the recommendations [6,7]. Traditional recommender approaches predict active users, preference based on the preferences of similar neighbor users whilst community based recommender systems exploit the tight groups of similar social interactions between the users [8, 9, 10]. Prediction for this approach comprises of neighbor users belong to the community of the target user. Trust recommenders consider that users’ preferences are most likely to be similar to their trusted friends. Based on this intuition, explicit and implicit trust recommender algorithms were proposed. The explicit approach use existing social interactions between users as trust statements. On the other side, implicit approaches make trust inferences on the basis of ratings. All the stated methods applied the trust declarations to predict unrated values to improve the worth of the predicted rates.

• III.    Proposed Approach

The prime challenge for recommender systems is the accuracy. An accurate prediction approach for the unrated items marks better recommender system. To improve accuracy, in this paper we planned to suggest a novel approach to incorporate reliability in communitybased trusted recommender systems (CRTCF). Three steps are in use to make recommendations. First, construct a trust network based on users’ co-rating data and apply community detection algorithm to identify community structures in the network. Second, compute initial prediction rating, reliability measure and reconstruct the trust network with new neighborhood. Finally, predict the ratings of unseen items and provide recommendations same way as the traditional community-based CF approach. Complete descriptions as well as the intuitions of the proposed approach are given in the following sections and shown in Fig. 1.

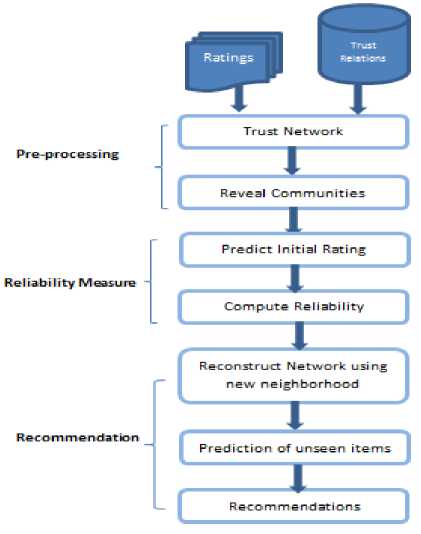
Fig.1. Outline of the Proposed Framework

where similarity represents the similarity between a , u and r denotes actual rating.

2 (ru,i - ru )sSimilarityau uE Ka, i prediction, i = ra +-----^------------.---- (2)

A Similarityau u e Ka, i

The similarity can be computed in many ways. Common approaches are Cosine Similarity and Pearson Correlation.

In the process of reducing the neighborhood size, traditional recommender systems compel taking all similar items into consideration when calculating users’ preferences. On the other side community-based recommender systems rely only on items that belong to candidate items’ community as expressed in (3).

pr^ediction a, i = r a +

• 2 ⁽ r u , i - r u ). ^Similarity au

u eC _______________________

21 Similarityau\ ueC

• A.    Pre-processing

This step comprises in building a network in which trust relations are represented based on the user co-rating entries. Indeed, two vertices (i.e., items or users) interact with each other if at least one user provides the rating to both of them. It is vital to note that, in this approach, the vertices are the users and hence the tight cluster of users is the community. A community can be well-defined as a set of items that are extremely connected to each other either materially and semantically [11, 12]. These learned communities will be exploited to guide the recommender system to predict users’ upcoming interests based on specific categories.

Label propagation algorithm [13] uses network structure as the monitor to reveal community structures. Each node is given a single label, and at each run, every node adjusts its label to the one agreed with the foremost number of its neighbors. In this repetitive process, the highly connected groups of nodes amend their different labels into the same label and nodes with the identical label will be grouped into the same community. To reveal community structures, we used LPA and (1) is used for labelling [14].

community, = arg max У, labels

J ilNeighor.^ (У

• B.    Reliability Measure

Predicting Initial Rating

Users’ preferences are computed using widely known recommendation method, namely Item-based Collaborative Filtering which concerns average ratings of identical items by the similar user as expressed in (2)

Where C is set of items which belong to the community of item j , r is the rating and similarity is the similarity value using Pearson correlation measure. Our proposed approach uses (3) for predicting the initial rating.

Reliability Computation

The traditional recommenders operate on user-item rating matrix for predicting unknown ratings for recommendations. Hence, investigators cringe to study the reliability based recommender systems to suggest more personalised and precise recommendations to users. Various methods have been offered to address difficulties facing by recommender systems. In this framework, network for the active user is created by the reputation of users which is figured by spreading trust. Trust statements are calculated in addition to Pearson correlation similarity measures between users. The subsequent equation is used to compute the trust statements between pair of users [15].

mpd -d(a,u)+1

T (a,u) = —----—--- mpd

Where mpd is the maximum propagation distance and d ( a , u ) is the distance between the users. Finally, the combined weight between pair of users which is denoted by W ( a , u ) is calculated as in (5). [16].

W ( a , u ) = 2* _S^imil^arⁱly„ * T ^{( a} , ^u)          (5)

similarity_au + T ( a, u )

Computed value of (5) is equivalent to T ( a , u ) when addition and multiplication of _similarity and T ( a , u ) is non-zero and its value is equivalent to _similarity when T ( a , u ) / 0 finally its value is 0 if similarity _{а u} * 0 and T ( a , u ) = 0

Where, T is a trust statement between the users a and u and similarity is calculated as shown in (6).

similarity _{a , u}

2 ( r ^{( a} ) - ^r ( ^{a ))(} r ⁽ u ) ^{- r} ( u ))

i = A;   (6)

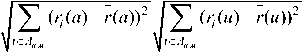
Where, r ( a ) is the rating given by the user, r ( u ) is the average ofratings given by the user u . Our framework modified (3) by replacing rating with weight for predicting unknown ratings which is shown in (7).

fnegttive ^(Va , i )

Max ( r ) - Min ( r ) - V_a , i A⁷ Max ( r ) - Min ( r )    J

Where, ⁷ =---------In⁰.⁵------- (i i)

Max ( r ) - Min ( r ) - V Max ( r ) - Min ( r )

2 W ( a , u )( r_u , i - r - prediction_a , i + r_a ) 2

u eC ________________________________________

• V , i =             2 W ( a , u )

u e C

V is the median of V _{a , i} , Max ( r ) , Min ( r ) are the maximum and minimum ratings of the items in a recommender system.

The reliability metric RLa,i is used to assess the quality of the predicted ratings. If RLa i > 0 , then predicitona, i = ra +

2 ⁽ r u , i - r u )W ^{( a} , u )

u eC ___________________

2 W ( a , u )

u e C

prediction _{a , i} is added to user-item rating matrix. In the proposed framework the value of the threshold is set to 0.6. otherwise,useless users are removed based on threshold values a and в .

Where, r denotes to the average of ratings for the target user a , u e C is a set of neighbors for the active user and belongs to the same community of item i , and W ( a , u ) represents the merged value of similarity and trust.

To evaluate the accuracy of the predicted rating we use reliability measure, a metric suggested based on the positive and negative sentiments. This metric uses only user-item ratings within a community to compute the worth on the accuracy of predicted rating and to provide a response on the quality of these ratings [16]. This metric is computed as shown in (8).

n f —( f         (4    1 f         (V f ^fp'-;t;v.' ⁽ Sa , i ) A ^{1+ f}posttive ⁽ Sa , i )

R ^L a , i = ^{( f} positive ⁽ S a , i ) ^{. f} negative ⁽ V a , i )             )

Where, f _positive ( S _{a , i} ) and f _negative ( V _{a , i} ) are positive and negative issues of the reliability measure. The positive issue is calculated by [16]:

f positive

(S )=1- ^S a,i        _S+Sa,i

Where S is the median rating of 5 and S = z W a,i             a,i               a,u ueC

C is a set of neighbors belongs to the community of item i . Furthermore, the negative issue is computed as in (10)

• IV.    An Illustrated Example

In this section, an example is exemplified to designate the step by step process of proposed method to generate predictions for unrated items as shown in Fig. 2. Suppose there are nine users and nine items, denoted by u and Ij respectively, where j , k e [1,9] . Based on interest, user may rate a small fraction of items ranging between 1 and 5 as shown in Fig. 2(a). In addition to it, trust matrix is shown in Fig.2(b) where each non-zero entry represents trusts relation between two users. The persistence of this instance is to apply the suggested approach to predict the rate of item i for the user u .

[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]

[1,] 334000000

[2,] 034300020

[3,]     0 4 3 3 3 0 0 0    0

[4,] 000320000

[5,] 000033400

[6,]     0 0 0 0 5 3 0 3    0

[7,] 003200200

[8,] 000020014

[9,] 000053003

• (a)    The User-Item Rating Matrix

[1,] .11 ......

[2,] ..11

[3,] .1.1 .....

[4,] .          1.

[5,]11..

[6,].......1.

[7,] ..11

[8,] .         11

[9,] ....11...

• (b)    Trust Information Between Users

( (1,2), [1,3], [2,3], [2,4], [3,4], [3,5], [4,5], [5,6],

[5,7], [6,8], [7,3], [7,4], [8,5], [8,9], [9,5], [9,6] ]

(c) Co-Occurrence Relations

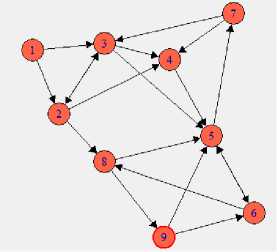
(d) Trust Network for an Active User u

> community

[1] 111112122

(e) Two Communities Detected after Applying Community Detection Algorithm.

Fig.2. Required Essentials for the Subsequent Phases

The first step of the proposed approach is to find the trusted relations of the current user by letting trust propagation in the trust network. Fig.2(b) provides a direct trust relation between users. For indirect relations we use trust propagation in the network which can be determined by (4) and the computed results are offered in Table 1. In particular, as a current user, u always turn to himself in providing precise ratings and hence t _u = 1 .

According to Table 1, users u and u are directly connected to user u , their trust relations will be 1.0, i.e., d = 1 their relations are shown in ego-centred network in Fig. 2(d). For user u , the distance from user u is 2, i.e., d = 2 . The shortest trust propagation path is U ^ u ₂ ^ ^M 4 . Since user U ₄ is not direct trustee to user

T ( u 1 ,u 4 ) = (3 - 2 + 1) /3 = 0.66 . For easiness, in this example we fixed max( d ) = 3 and K = 3 to select nearest neighbors [9]. Note that the trust relation of user u is zero due to the maximum propagation distance constraint, i.e., max( d ) >  3 .

A set of neighbors for current user u using traditional CF approach are { u ₂, u ₃, u ₄, u ₅, u ₈, u ₈} and users { u ₂, u ₃} may be considered for prediction since they are positively correlated with the target user. The proposed approach reduces the neighborhood by considering the similarity as well as the users’ who belong to the community of the target user. Hence the trusted users of u are { u , u , u , u } although the user u is resided in the same community of the target user he/she is not considered for prediction since his/her maximum propagation distance is zero. Therefore the concluding weights between the current user and the other trusted users using (5) are -1.44, 0.65, -1.15 and 0.16, respectively. After considering the value of k , users u , u are taken as nearest neighbors.

Table 1. Trust Propagation Between Users

	1	2	3	4	5	6	7	E	9
1	1.33	1	1	0.66	0.33	0	0	0	0
2	0	133	1	1	0.66	033	0.33	0	0
3	0	1	133	1	0.66	033	0.66	0	0
4	0	0	033	133	1	0.66	0.66	033	0
)	0	0.33	0.66	0.66	133	1	1	0.66	033
6	0	0	1	0	0.66	0.33	0.33	1	0.66
7	0	0.66	1	1	0.66	133	1.33	0	0
8	0	0	0.33	0.33	1	0.66	0 66	1.33	1
9	0	0	0.33	033	1	0.66	0.66	0.66	1.33

The remaining weights between the current user with all other users is shown in the subsequent tables.

u , the trust is calculated by using

• Table 2. Weight Matrix Between Every User with All Other Users

• > weightmatrix

[,1]          [,2]         [,3]         [,4]         [, 5]         [,6]         [,7]          [,8]         [,9]

[1,]  1.1428571 -1.44094868  0.6559556 -1.1546873  0.1654135 -O.25OOOOO -0.1767767 -0.22360680 -0.1865506

[2,1 -0.4187649 1.14285714  0.8915930  0.6090729 -1.7713427  2.0613846 -1.2300000 -0.04406526 -0.3676276

[3,1  0.4880461  0.89159296 1.1428571  0.6152150 1.33OOOOO 1.4387643 -0.5926012 -0.07936758 -0.4635034

[4,j -0.3093992  0.43788991  0.3808874  1.1428571 -1.3403756 -1.2300000 -0.5669060 -0.28829646 -0.4617489

[5,1  0.1100000  5.39209956 1.33OOOOO -2.0158871  1.1428571  0.8871716 -0.1261647  0.31522395  0.3156127

[6,1 -0.2500000 -0.49266464 -0.6211496 -0.6187983  0.7261227  1.1428571  0.3431458  0.36548800  0.1838095

[7,1 -0.1767767 -1.45927880 -0.3720964 -0.4965339 -0.1302736  0.3431458  1.1428571 -0.31622777 -0.2638224

[8,1 -0.2236068 -0.04406526 -0.2083419 -0.2882965  0.3421906  0.3348886 -1.2031684  1.14285714 -0.1001193

[9,1 -0.1865506 -0.36762759  2.3738356  2.3971598  0.4611609  0.1926628 -0.8731991 -0.10268956 1.1428571

In the second step, the ratings of selected neighborhood are used for predicting the unrated item of the active user. In this example, the initial rating of the item i for the current user u without considering community is equal to 3.32 which obtained using (2). The same initial rating by considering community is equal to 3.08 which obtained using (3). Table 2 and

Table 3, shows the prediction values for all the users. Even though there is a fraction of change between the traditional and community-based approach, the nearest neighbors reduced from 5 to 3 and by using reliability it has still reduced to 2. In the proposed approach reliability metric is proposed on community-based CF recommender system.

Table 3. Initial Prediction without Considering Community

> internal predict!on

E.U      E.2]      [,3]      E,4]      [,5]      [,6]      E»U      E.8]

[1,] 3.000000 3.000000 4.000000 3.176989 3.328949 3.000000 3.794525 4.333333О

[2,] 3.333333 3.000000 4.000000 3.000000 2.819272 3.333333 2.811382 2.0000000

[3,] 2.916667 4.000000 3.000000 3.000000 3.000000 3.583333 2.758055 2.2500000

[4,] 2.833333 2.866188 2.491344 3.000000 2.000000 2.833333 2.1647301.5000000

[5,] 3.000000 2.852241 3.208314 3.336102 3.000000 3.000000 4.000000 4.3333330

[6,] 4.000000 3.386182 3.510415 3.536302 5.000000 3.000000 4.026103 3.0000000

P,] 2.666667 2.247231 3.000000 2.000000 2.715032 2.666667 2.000000 3.3333330

[8,] 0.000000 0.000000 0.000000 0.000000 2.000000 1.900979 0.000000 1.0000004

[9,] 4.000000 3.386182 3.235922 3.649285 5.000000 3.000000 4.177273 4.6666673

Table 4. Initial Prediction with Considering Community

> i nternalpredafter real i

[,U      [,2]      [,3]      [,4]      [,5]      [,6]      [,7]      [,8][,9]

[1,] 3.000000 3.395049 3.665728 3.083333 3.083333 3.000000 3.794525 4.3333330

[2,] 3.333333 3.328686 3.641709 2.719883 2.819272 3.333333 2.811382 2.0000000

[3,] 2.916667 3.671314 3.547810 3.258263 2.916182 3.583333 2.758055 2.2500000

[4,] 2.833333 2.866188 2.491344 3.000000 2.000000 2.833333 2.164730 1.5000000

[5,] 3.000000 2.852241 3.208314 3.336102 3.076740 3.000000 4.000000 4.3333330

[6,] 4.000000 3.386182 3.510415 3.536302 3.333333 3.3333334.026103 3.0000000

P,] 2.666667 2.247231 3.000000 2.000000 2.715032 2.666667 2.000000 3.3333330

[8,] 0.000000 0.000000 0.000000 0.000000 2.000000 1.900979 0.000000 1.0000004

[9,] 4.000000 3.386182 3.235922 3.649285 3.291056 3.000000 4.177273 4.6666673

In the third step, the reliability metric is calculated by using (9) to assess the worth of prediction rating. In this instance, the reliability value of the prediction is 0.369. For easiness, we set, median of the specific recommender system to 2 and 1, i.e., ( S , V ) in (9) and (10), respectively. The computed reliability value for the considered instance is less than threshold (i.e. 9 = 0.5). Therefore, in this case the proposed method is useful in order to eliminate untrusted users from the network of the current user. Assume that the threshold values of positive and negative factors are set to a = 0.5 and p = 0.5 . The negative factors of users u , u are 0.0017 and 0.0019. Since the calculated weight of the active user u is less than the threshold, the concluding rate for the current user is figured by considering the weight of only user u . Therefore, the final prediction is calculated by using (7), is equal to 3.08. The distance between every node to all the other nodes, initial prediction and final prediction by using reliability for the above instance are mentioned in Table 5.

Table 5. Item Prediction Using Reliability Measure

	I1	I2	I3	I4	I5	I6	I7	I8	I9
	0	1	1	2	3	4	4	5	6
	3	3	4	3.17	3.32	3	3.79	4.33	-
	3	3.39	3.66	3.08	3.08	3	3.79	4.33	-
	0	0	1	1	2	3	3	4	5
	2.66	3	4	3	2.81	3.33	2.811	2	-
	3.33	3.32	3.64	2.71	2.81	3.33	2.811	2	-
	0	1	0	1	2	3	3	4	5
	2.91	4	3	3	3	3.58	2.75	2.25	-
	2.91	3.67	3.54	3.25	2.91	3.58	2.75	2.25	-
	0	4	3	0	1	2	2	3	4
	2.83	2.86	2.49	3	2	2.83	2.16	1.5	-
Distance	2.83	2.86	2.49	3	2	2.83	2.16	1.5	-
Initial Prediction (with Community) Final Prediction (With Reliability)	0 3.66	3 3.06	2 3.01	2 3.33	0 3	1 3	1 4	2 4.33	3 -
	3	2.85	3.2	3.33	3.07	3	4	4.33	-
	0	5	4	4	2	0	3	1	2
	4	3.38	3.51	3.53	5	3	4.02	3	-
	4	3.38	3.51	3.53	3.33	3.33	4.02	3	-
	0	2	1	1	2	3	0	4	5
	2.6	2.24	3.00	2.00	2.71	2.66	2	3.33	-
	2.6	2.24	3	2	2.71	2.66	2	3.33	-
	0	4	3	3	1	2	2	0	1
	-	-	-	-	2	1.9	0	1	4
	-	-	-	-	2	1.9	0	1	4
	0	4	3	3	1	1	2	2	0
	4	3.38	3.23	3.64	5	3	4.17	4.66	3
	4	3.38	3.23	3.64	3.29	3	4.17	4.66	3

• V.    Results

In this framework, real-world dataset MovieLens is used in the experiments. The proposed framework is related to the pure CF (UBCF, IBCF), the basic trust model TARS [14], and the Merge algorithms [15]. The accuracy results shown in Table 6 demonstrated that the proposed CRTCF method attained lowest error and high coverage.

Table 6. The Accuracy Performance on the MovieLens Dataset.

All users	Measures MAE, RC, F1
	UBCF	IBCF	TARS	Merge	CRTCF
	0.953	0.912	0.892	0.795	0.721
	93.50%	92.20%	88.70%	91.30%	90.17%
	0.878	0.879	0.882	0.894	0.899

• VI.    Conclusion

Recommender systems provide personalized proposals for users on certain types of items to improve customer satisfaction and   retention.   Integrating additional information like community detection, trust is a concept that recently takes much consideration and has been reflected in social networks. In this framework, a unique approach is proposed to progress the quality of the recommender systems. Weight is computed between active user and the other users based on the similarity value and the trust value. Users above threshold are considered as neighbors. Prediction for the active user is computed by considering the neighbor user ratings resided in his/her community. Finally the reliability metric is figured to assess the worth of prediction rating. The acquired results from the experiments show that the proposed framework attained sophisticated correctness matched to those of the state-of-the-art algorithms.