A modification of Dai-Yuan’s conjugate gradient algorithm for solving unconstrained optimization

The conjugate gradient method (CGM) is one of the most widely used approaches for solving nonlinear optimization problems. We consider the following unconstrained optimization problem:

min ^f (x),                                         (1)

x∈Rn where f (x) : Rn ^ R is continuously differentiable and bounded below when solving equation (1), the iteration method is employed and is written as:

x _{r +1} = x r + a r d r ,                                   (2)

where α r is a line search-based optimal move [1]. One of the most inexact line searches is the Wolfe conditions to achieve convergence in the conjugate gradient methods, α r is guaranteed to be present as:

f (x r+1 ) - f (x r ) <  ba r Vf (x r ) ^T d r ,

(3a)

| g r+i ^T d r I <-agr^Td r ,                          (3b)

where 0 <  5 <  a < 1. More information may be found in [2]. The directions d r are calculated using the following rule:

(    -g r+i     ; for r = 0

( -g r+i + e r d r ; for r >  1

where βr ∈ R is a conjugacy coefficient. There are many Conjugate Gradient techniques based on different βr process choices, for example [3–8]. The most significant distinction between the spectral gradient approach and the gradient conjugate method is calculating the search path. The spectral gradient method’s search path is as follows:

d r+1

^ r+1 g r+1 ^{+ в} Г s r ¹

where s r = a r d r and 6 _{r +1} is the spectral parameter. The spectral conjugate gradient is a powerful tool for solving large-scale unconstrained optimization problems. The spectral conjugate gradient algorithms are presented in many papers, for more details see [9–20].

1.    Derivation of New Parameter

An essential idea is to equate the vector of the conjugate gradient method to the vector of quasi-Newton method such that d ^Q +N = d^G then

^p r ^H r + 1 g r+1      9 r + 1 g r + 1 ^{+ e} r s r ¹

where the matrix H _{r +1} is positive definite and symmetric, and we use the scale from [21] defined as follows:

yrT yr pr srT yr

.

We use the DY conjugate gradient algorithm because it achieves convergence according to the Wolfe criterion and has the same property as FR [4] because it is similar in the numerator and the same property as HS [3], which is similar in the denominator. Therefore,

y T y r И           .^>+^«

H r + 1 g r + 1       " r + 1 g r + 1 + m     s r ¹

s _r ^T y r                                 s _r ^T y r

y _r ^T y r _T

--T--yr Hr+1gr+1 = srT yr r since Нг+1Уг = Sr ^ yTHr+1 = sr,

t„

—O r+1 y r g r+1 +------ y r s r ^{1 r}            s _r ^T y r   ^r

yTyr sr gr+1 = sTyr r

^— +r + ¹L^{y g} gr+1 + ^{| g} r+1 ^ -

Then the new spectral is known in the following form:

лSDY _ ll^gr+1^   I

"r+1       rp + yrT gr+1

y r^T y r s _r ^T y r

^s T g r+1

y T g r+1¹

then the proposed search direction is defined

as

d - igr +1i\ d r+1 = -           Г

[ yT g r+1

/ y T y r A sT_g r+il \ ^S T Уг) y T g r+1 J

■ gr+1 +   т sr- r+1     srT yr

Lemma 1. Suppose that the sequences generate (2) and (10) computed by line search (3a) and (3b), then the sufficient descent condition holds.

Proof. Define the spectral gradient direction as follows:

SDY       DY dr+1 = °r+1 gr+1 + pr sr1

where θ _r ^S ₊ ^D ₁ ^Y is defined in (9)

,         Г 1к+111\ ( y T y r A sT Sr+11       Jgr+111²

d r+1 = ^— —---- +        —---- g r+1 +   T---sr •           ⁽¹¹⁾

y _r ^T g _{r +1}       s _r ^T y r   y _r ^T g _{r +1}     ^r+1      s _r ^T y r

Multiply equation (11) by (^r^1^). We get dT+1 gr+1 = - [ l|gr+1||2 , (yTУг A sT gr+11 l|gr+1||2 , l|gr+1||2 sT gr+1

||g r+1||2           y T g r+1    VT Уг) y T g r+1   | g r+1 | 2      s T У г | g r+1 | 2 •

Since yTgr+1 < lyr|| |gr+1| and sTgr+1 < sTyr, then dT+1 gr+1 <   |gr+1| _   hr II    sT gr+1

| g r+1 | ² <      ly r I       | g r+1 | ⁺ s T y r •

From the strong Wolfe condition, sTgr+1<—a sTgr, and since we get sTgr<——yr dT+1 gr+1 /   Ilgr+AI      |yr1    _(^+l"|yr1 , a

< a <         tH •

||g r+1 l ^{2             |} Уг ^l        l|g r+1 ^{l        s} T y r           ||g r+1 ^{l a} +l

Since y r =g r+1 — g r we get:

^d T+1 g r+1 < - ^l g r+1 ^— g r l , ^a < - ||g r+1 ^l , ^a

||g r+1l2           ll^gr+1 ^{l      a} +l         ll^gr+1 ^{l a} +l

Let ^ = (1 — y+1) then we get:

^d T+1 g r+1 < ^— ^1^+1112 .

□

2.    Convergence Analysis of New Method

Assumption I . The following are some fundamental assumptions in this paper. (a) The level set Q is bounded. (b) The function is convex and continuously differentiable, its gradient g (x) is Lipchitz continuous, i.e., there exists a constant L >  0 such that | g(x) — g(y) | <  L | x — y | for all x,y G Q.

Lemma 2. Suppose that Assumption I holds then for any CG-method, the direction d _{r +1} is a descent, and the step size α _r is achieved by (3a, 3b) if

E r>1

K+1f

= TO .

Then

lim (inf | g r | = 0) • r ^^

Lemma 3. Suppose that Assumption I holds, where d r+1 is defined by (10) , then the method satisfies equation (12) .

Proof. Since в DY is positive [7], then 0 <  в < 1,

Л ^{| e} D ^{Y |}<  ^ 1 ,^ 1 > 0,

ICT I <

\ 6 SDY

g yrTgr+1

+

lg r+1 1 2

l|gr +1 ^{| 2} - kT +l gk ¹

+

(М2)

s _r ^T y r

( М2 )

\ sr yr /

s ^T g r+1 y r ^T g r+1

,

-as'T o„ rr

l|g r+1||² - ^| g T+1 g r ¹ ,

from Powell restart \g' T ₊₁ g r | > 0, 2 ||g _{r +1}||² ,

^SDYI < jg +i ^E 0,8 B g r+1 B ²

+

• 2        s r^T y r

hr1 C+12

s T y r 0,8 lg r+1 12 ’

ICT I < 2,

From equation (5) and using (13) and (14) lldr+1 № < hl|gr+1||2

^ 2 > 0.

∞

E

k ≥ 1

+ ^1 || sr || = ^ 3 ,

1          1

—;--„ > — > 1 = TO.

• ¹    dr+1¹   ^3 C

3.    Results and Discussion

□

In this section, the new algorithm specified by equation (10) is compared to the classical DY algorithm [7] as well as AMDYN algorithm [11], which define θ r+1 as follows:

Д _      ¹ Li ||2    ll^gr+1^|2 (s ^T gr +1 ) , T ]

^d r+1 =   ----- ^{| g} r+1¹-- f--+ s r ^g r+1 .

y _r ^T g r+1                     y _r ^T s r

We chosen 65 unconstrained optimizations in the range [n = 1000, 2000,..., 10, 000], broadly and based on generalized [22]. All algorithms used Wolfe condition a = 0, 9,5 = 0, 0001. The codes are adopted with double precision and using the Fortran language. All of these codes are authored by Andrei [11,23]. We applied the performance profile of Dolan and More [24] to demonstrate the algorithm’s efficiency, where the upward curve indicates that the new algorithm (SDY) is better than the classic DY. Also, we compare the results with AMDYN based on the number of iterations (NOI), number of functions and gradient ratings (NOF & g) and CPU time (time). Representation of practical results is presented in Figure.

Conclusion

The aim of this work is to propose new computing schemes for the spectral parameter θ _r ^S ₊ ^D ₁ ^Y . This technique is such that the search direction always possesses a sufficient descent property. As a result, the presented new spectral conjugate gradient possesses global convergence under a robust Wolfe search. Using a collection of 65 optimization tests to solve problems, and numerically comparing the conduct of this new algorithm to that of some conjugated gradient algorithms DY and AMDYN, we show that the proposed algorithm outperforms previous conjugate gradient algorithms due to computational performance.

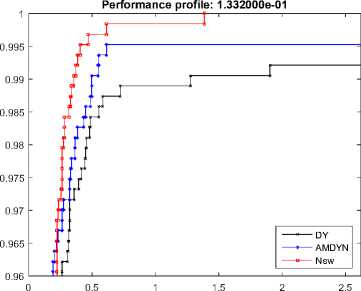
(a) NOI

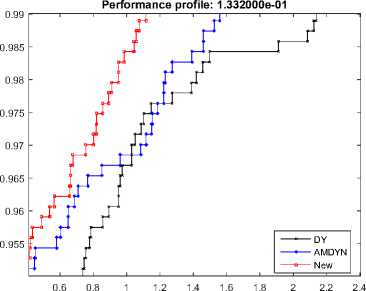
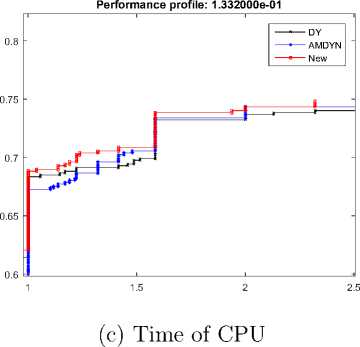
Performance profile