A numerical method for solving quadratic integer programming problem

Recently, nonlinear integer optimization is of particular interest due to its practical importance. Consider the model problem in the following form:

n2

^E (PZX i) -^ min

52 X i <  min (S,A), i=1

where all parameters are integers. Problem (1) arises in the problem on formation of the optimal order for education institutions in a region (see [1]), which can be reduced to the simpler problem of the form n /   \ 2

i= (Z i) —^ ^min n

I EA i = E,

X i=1

n where E = 52 Pi — min(S, A) and Zi > 1 are nonnegative integers, Ai, 0 < Ai < E(i = i=1

• 1,    2, ...,n) , are unknown nonnegative integers.

n - 1

The change of variables A n = — 52 A i reduces the problem to a very special case of the i=1

box-constrained integer least squares problem (see [2–4] and the problem on the closest point search in lattices (see the survey [5, 6]), as well as the closest vector problem). General problems of this type are NP-hard (see [7, 8]). However, at present, there exist rather effective methods for solving these problems (see [3, Ch. 8; 6, 9–11] and the bibliography therein). The method proposed below is very simple and actually exact, and allows to involve a large number of the variables. Numerical experiments show an almost linear dependence of the computation time on the number of variables, from O(n) to O(n • ln(n)).

1. Main Results

First of all, we give some theoretical justification of the algorithm. Consider the

minimizer of problem (2) in the form λ _i ^∗

where the number Z _n+1 E (0, to ) is to be determined.

= [в • 0, 5 + 0, 5] , e i = (zZ +1) ² (i = 1, 2,

,,ⁿ⁾ ,

Lemma 1. If there exists Z _{n +1} E (0, to ) such that

n

E = Е в • 0, 5 + 0, 5], e i = i=1

к Z n+1) '

then the numbers

A * = [e i • 0, 5 + 0, 5], e i =

( _Z_ у

V Z n+J

(i = 1, 2,..., n)

give the minimum of functional (2).

Proof. Represent λ _i ^∗ in the form

A * = e i • 0, 5 + 0, 5 - X i , e i =

Z i

Z n+1

(i = 1,2,...,n),

where x i E [0; 1) . Show that

+»I =+A

n for all integers Mi such that ^2 Mi = 0.

i=1

Taking into account (3), present expression (4) as

^{E 2} • ^A i * • M i ⁺ /' ² >  0

Z2      " ’ i=1           i n E i=1 n

^e i • ^M i ^{+ M} i    ² • ^x i • ^M i ^{+ M} i

^^ ^M i i=1

^Z i ²

- 2 • x _i • M _i + M _i ²

> 0,

n

E ^{M i}

Z i ²

-

2 • X i • M i + M i ²

n

+ E yMi- >  0, i=1 ^{Z n+1}

> 0.

i=1            ^Z i ²

Since м 2 >  M i for all integers M i , inequality (5) is valid for all x i E [0; 1) . Therefore,

expression (4) is also valid. This completes the proof.

□

Consider the function

F (Z n+i ) =

• 0,5 + 0,5I

which does not increase in the variable Z n₊₁ and takes nonnegative integer values. Obviously, if Z i = Z , (i,j = 1...n) , then the function F (Z _n+1 ) has the jump equal to n at the discontinuity point. Therefore, the function F(Z _{n +1} ) does not take all integer values. Consequently, depending on the variable Z i , the range of the function F(Z _{n +1} ) cannot coincide with the set of natural numbers. At the discontinuity point, we have

F(Z n₊i ± 0) = c т d, where c, d are nonnegative integers and d >  1 . Since the functions

(• 0,5 + 0,5, i = 1,2,...,n

\ Zn + 1 / are continuous, then the function

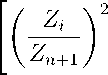
0, 5 + 0, 5

is a nonincreasing piecewise constant function taking all natural values when the independent variable run over the nonnegative semi-axis. The sum of these functions is also a nonincreasing piecewise constant function, and takes all nonnegative integers whenever all discontinuity points of these functions are different. Otherwise, this statement is not true. If two discontinuity points coincide, then the module of the jump is not less than 2 at each of these discontinuity points. Let us consider quantity (7) to be equal to a nonnegative integer k . We find that the discontinuity points of functions (8) have the form

Z n+1 = Z i /(2k - 1) ^1/2 , (k = 1, 2,..., X .

Two discontinuity points coincide whenever there exist nonnegative integers k and m (for i = j ) that not exceed n and

Z i /(2k — 1) ^1/2 = Z , /(2m — 1) ^1/2 , (k = 1,2,..., x, m = 1, 2,..., x ) . (9)

These equalities hold for different pairs of numbers Z i and Z j . Consider the segment [a, b] such that F (a) >  E and F (b) <  E . Function (6) is piecewise constant, and the segment [a, b] has q discontinuity points. Denote these discontinuity points by Z ^l _{n +1} , l = 1, 2, ..., q , and enumerate in increasing order with respect to the number l . Consider the following two possible cases.

1. There exists the number l such that F (Z _n+1 ) = E for all Z _{n + l} in (Z n_{l +} ¹ ₁ ,Z n ₊₁ ) . By

Lemma 1, the numbers λ _i ^∗ for these numbers Z _{n +1} .

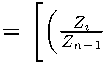
0, 5 + 0, б] give a solution to problem (2)

nn

In this case, E + a = ^A i and E — b = J2 A², where a and b are nonnegative i=1                       i=1

integers. Note that for m = a + b there exists the jump of the function F at Z^n+1(m = F(Zln+1 — 0) — F(Zln+1 + 0)), and, hence, a, b < m. Consider the problem n2

E (V)   ■ min, i=1 x      7

n a = Ey, i=1

where the numbers y i are nonnegative integers. Consider numbers (10) such that the corresponding functions A ¹ (Z _{n +1} ) has the discontinuity point at Z ^l n ₊₁ . Assume that these numbers are A 1 , A 2 , ..., A m , else renumber these numbers. The remaining functions A ¹ (Z _n+1 ) are continuous at this point for t >  m + 1 .

Lemma 2. In Case 2, the solution to problem (2) can be represented as Ai = Ai — yi, if m yi = 0 for i = m + 1,..., n and yi E {0,1} for i = 1,..., m, a = 22 yi.

i=1

Therefore, problem (2) is reduced to the following problem having the less dimension:

{ ^m / a 1 - \ 2

E (' min, i=1        7

m a =    yi , i=1

where the minimum is taken over the numbers y i E { 0,1 } .

Proof. Let us show that there exist numbers yi E {0,1} (j = 1, 2, ...,m) such that n /.1x2 m / \ 1 x 2 n /-.1, x 2

.E .® ■ ^E        -E( ')

n for all integers ci, if —a = ^2 ci. Transform (12) as follows:

i=1

n / \ 1 \ 2 m / \ 1 \ 2 m E ^ + E Zj + E t=m+1 ' t2 j=1 j/ j=1

y^{) 2}

(Z j ) ²

-

2y j^l R ² ₊ E (Z j ) ² "  1=1 VzJ ^=1

(C i ) ²

(Z i ) ²

, 2c i A| ⁺ (Z i ) ² .

By construction,

2A j = Z,ljU ) ² + 1, j = 1, 2,...,m,

2A i = (ZZZ J-1) +1 — 2a., i = 1, 2,...,n,

where a i is the fractional part of the quantity 2 rewrite (13) in the form

2 ц ZA +1) y\ ^Zn +i/      у

. Taking into account (14),

(       y j (f zZ j- ) ² + 1)      n / A 2 Ci (f Ze- ) ² + 1 — 2aJ

(y j ⁾² _       ^Z n +^       < ^{e (}C i ^{) 2}      yv ^Z n +1/ ___________ У

(Z j ) ²            (Z j ) ²         "  1=^ (Z i ) ² +            (Z i ) ²

i = 1, 2, ..., n, i = 1, 2, ..., n.

which can be transformed as follows:

m

Е j=1

⁽ У з ^{) 2} - У з

(Z j ) ²

-

m yj j=1

(z n+1 ) ²

≤

(c i ) ² + c i (1 - 2a . )     £ c i

(Z i ) ^{2         +} (z n+1 ) ²

m

Substitute    yj j=1

= a and ^2 c i = — a in (32):

m

Е j=1

⁽y j ^{) 2 —} y j

(z j ) ²

n

5 Е

^(c i ^{) 2 +} c i ^{(1 — 2a} i ) ( Zip

The function £ (y j Z — y j j=i    j

has a zero global minimum, which is achieved for y j E { 0,1 }

m such that a = ^ Уз■ These numbers yj exist, since a < m. Therefore, the left-hand j=1

side of (15) is removed, while the right-hand side is always nonnegative for all admissible numbers c i .

□

Lemma 3. The minimum of functional (11) is equal to m /\1\2 stУ

-

a

,

m and is achieved for every set of the numbers yi E {0,1} such that a = ^yi.

i =1

Proof. For example, consider the following set of numbers: y j = 1 for j = 1, 2,..., a and y j = 0 for j = a + 1, ...,m . Consider the objective functional (see (11))

j

² + s (M-t=j+1 ^{v 7}

Transform the expression ab ove and arrive at the quantity

Е ( — 2 ( ^ b ) + ( z )j + s ( b-

Substitute (10) in (16) and obtain

α

E — 2

² • 0,5 + 0,5) • y,^

j =1

\

\

Z j ²

/

+(S)

/

^m /\1\² ' Е Z .

i =1

.

Transform (17) and obtain the expression ^m 1 ² Е ft) ^—

Obviously, this expression is independent minimum of functional (11).

a

^Zn+if- of the numbers

y j , and, therefore, is the

□

The main result is as follows.

Theorem 1. There exists the number l such that either F (z n ₊₁ ) = E for all z n ₊₁ in (Z n-X , z n ₊₁ ), or F(Z^l _{n +1} - 0) > E and F(Z^l _{n +1} + 0) = F (z n+1 — 0)

Г/ \ 2

the numbers A i ¹ = (zZ ii) ' 0, 5 + 0, 5 give a solution to problem (2) for the numbers

Z _{n +1} in (z ^₊i ,Z n ₊₁) . In the second case, suppose that m is the jump of F at Z ^l _{n +1} and A ¹ , i = 1, 2, ...,m, are the functions having a discontinuity point at Z ^l _{n +1} (otherwise, we

n can renumber). Let a = ^2 A1 — E. Then the minimum of functional (2) is achieved at i-1

the numbers Ai = Ai1 — yi, if yi = 0 for i = m + 1, ...,n, yi E {0,1} for i = 1, ...,m, and m a =    yi .

i-1

• 2.    Description of Algorithm

First of all, we find the segment containing the necessary discontinuity point z ^l _{n +1} .

Lemma 4. Suppose that F(zln+1 — 0) > E and F(zln+1 + 0) < E, then below zn+1 =

n

E zi

\ i ^-1

\ 2E +

l          above n < zn+1 < zn+1 =

n

E zi

\ J^-! \ 2E

.

- n

Proof. F(z ^l _{n +1} — e ) >  E for every e >  0 . We have that

n

n

E = 5^ • 0, 5 + 0, 5] <  ^(в • 0, 5 + 0

i -1

Hence, we obtain that

i -1

, 5) в = (

Z i ^{l z} n +1

-

ε.

l zn+1

-

above

^E <  ^z n+1

n

E zi

= \ — \ 2E

.

- n

On the other hand,

n

E = ^ [e i • 0, 5 + 0, 5] i -1

and, therefore,

n

> V ■ • 0, 5 + 0, 5,ei = ( i-1

Zi zn+1+E

,

below zn+1

n

E zi

= \ i ^-1

\ 2E +

— < ^z n+1 ^{+ e}- n     ^{n +}

The number e >  0 is arbitrary. This completes the proof.

Describe main steps of the algorithm.

1. Determine the quantities

□

a

n

E zi

= \ ^J-1 \ 2E

-

n

E zi

i -1

— , b = A —----• n      2E + n

If F (a) = E or F (b) = E , then, for the known (by Lemma 1) solution, we have that

A * =

( Za i ) 2 • 0, 5 + 0, 5 or A * = ( Zb i ) ² • 0, 5 + 0, 5 . Otherwise, go to Step 2.

• 2.    Use the algorithm of the dichotomy method [12]. There are two possible situations.

First, we find Z _n+1 such that F (Z _n+1 ) = E . Then A * =

Z i

\ Zn +1 /

• 0, 5 + 0, 5 is a solution

to problem (2). Second, we find an interval (a, b) containing only such discontinuity points of F that F (a + 0) = E + a or F (b — 0) = E — в , where а, в >  0 are integers. Then go to Step 3.

• 3.    Find the discontinuity point Z^n ₊₁ of function (6) on the new interval (a, b) . We 2

have that F(Z^l n ₊₁ ) >  E . Calculate A i ¹ = ZZZr^j • 0, 5 + 0, 5 and look for a solution to

problem (2) in the form A * = [A 1 — 1,..., A a — 1, A a ₊₁ ,..., A m ,

..

A } (Z n+i ) , j = 1,

.,А П ] , where the functions

..

.,m have a discontinuity point at Z nn ₊₁ , while the remaining functions

A 1 (Z ^l n ₊₁ ) , t >  m + 1 , are continuous at this point.

• 3.    Realization of Algorithm

In order to realize the proposed algorithm, we use the language “Python” and the service GitHubGist. The service is an open remote control system to verify software and numerical experiments. The algorithm was applied to different sets of data (see Table 1).

Table 1

Numerical experiment scenarios

№	Number of variables, n	Number of experiments
1	10	500
2	100	500
3	1000	500
4	10000	500
5	100000	500
6	1000000	500
7	10000000	500
8	100000000	500

Analyzing the algorithm, we can note that a solution can be found at every step of the algorithm. Hence, we pay attention to the following two problems.

First, obtain the dependence of the computation time on the number of variables (see Figure). Second, obtain the probability to find a solution at every step of the algorithm (see Table 2).

The results of the numerical experiments and their realizations can be found at

Conclusion

According to Figure, the dependence of the computation time on the number of variables is almost linear and is at most O(n7n(n)) . Also, note that a solution is determined at Step 2 in 83 % cases, while Step 3 gives a solution in the remaining 17 % cases.

10 10л2 1ОлЗ 10л4 10л5 10л6 10л7 Number of unknowns 10л8

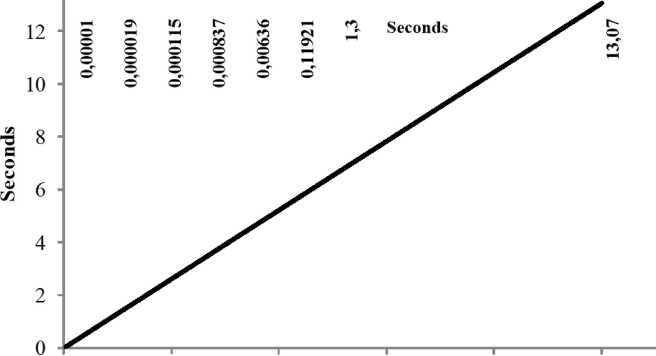
0     20000000 40000000 60000000 80000000 100000000

Number of unknowns

Computational complexity of the algorithm

Table 2

Probability to find a solution at every step of the algorithm

Number        of	Number of solutions	Number of solutions
unknowns	determined at Step 2	determined at Step 3
10 1	3288	712
10 2	2861	639
10 3	2479	521
10 4	2076	424
10 5	1670	330
10 6	1247	253
10 7	846	154
10 8	440	60
Average probability	0,836	0,164