Acceleration of summation over segments using the fast Hough transformation pyramid
Автор: Soshin K.V., Nikolaev D.P., Gladilin S.A., Ershov E.I.
Рубрика: Программирование
Статья в выпуске: 1 т.13, 2020 года.
Бесплатный доступ
In this paper, we propose an algorithm for fast approximate calculation of the sums over arbitrary segments given by a pair of pixels in the image. Using the results of intermediate calculations of the fast Hough transform, the proposed algorithm allows to calculate the sum over arbitrary line segment with a logarithmic complexity depending on the linear size of the original image (also called fast discrete Radon transform or Brady transform). In this approach, the key element of the algorithm is the search for the dyadic straight line passing through two given pixels. We propose an algorithm for solving this problem that does not degrade the general asymptotics. We prove the correctness of the algorithm and describe a generalization of this approach to the three-dimensional case for segments of straight lines and of planes.
Search for segments, fast hough transformation, discrete radon transformation, brady algorithm, fast discrete radon transformation, dyadic pattern, beamlet pyramid
Короткий адрес: https://sciup.org/147232979
IDR: 147232979 | УДК: 004.021 | DOI: 10.14529/mmp200110
Текст научной статьи Acceleration of summation over segments using the fast Hough transformation pyramid
In the paper [1], D.L. Donoho and coauthors propose an approach to multiscale image analysis called the beamlet analysis . The approach allows to construct detectors of objects (segments having unknown position, length and orientation; circles having unknown position and diameter, etc.) on highly noisy images [2]. From a practical point of view, the proposed approach has a drawback, since a complex pre-calculation is necessary. Indeed, for an input image, all beamlet analysis algorithms assume that the beamlet dictionary is pre-calculated as a set of segments having various orientations, while the position and length of the segments are chosen in a special way. However, the authors do not discuss the computational complexity of constructing such a dictionary and do not propose algorithms to calculate the dictionary. Therefore, it is difficult to estimate the practical applicability of the approach as a whole. The paper is devoted to the issues of the pre-calculation complexity, as well as the fast finding of the sums over arbitrary segments in the image as a whole.
Let us describe the approach proposed by D.L. Donoho and coauthors in more detail. The approach involves construction of a dyadically organized beamlet dictionary. The authors consider an image as a function of two variables defined on a discrete lattice in the square [0,1] 2 with the discretization step 1/n, where n = 2 p , p E N , and the length of the segment is defined as a number of pixels formed the segment. Then the dyadic square
S(k 1 , k 2 , q) is the set of points [k 1 /2 q , (k 1 + 1)/2 q ] x [k 2 /2 q , (k 2 + 1)/2 q ] on the plane. Here q defines the level of the dyadic square, and (k 1 , k 2 ) define the position of the square, where 0 < q < p and 0 < k 1 , k 2 < 2 q — 1. In particular, the whole image is the dyadic square S (0, 0, 0) of the level 0, and an arbitrary pixel having the coordinates (i,j ) is the dyadic square S(i,j,p) of the level p. A beamlet is a segment having arbitrary orientation whose ends belong to the sides of the same dyadic square. The coordinates of the beamlet ends are also given with a certain discretization, and the discretization quantum can be taken to be equal to or smaller than the size of a pixel. In the present paper, we consider only the first case, while the subpixel discretization is not of our interest.
By a beamlet transformation we mean an integration of an image over all possible beamlets in the dictionary. For an image of the size nxn pixels, the beamlet transformation allow to construct a beamlet pyramid containing 0(n2 log n) values. The beamlet pyramid is the basis for the approach to image analysis proposed by D.L Donoho and coauthors [2], and the issue of calculation of the beamlet pyramid is considered, in particular, in the present paper.
The most obvious way to calculate the sum over pixels of a segment is to sum the values of these pixels. Further, we refer to an algorithm based on this obvious way as the “naive” algorithm. If segments have a significant intersection (such a case is typical for the beamlet dictionary), then the “naive” algorithm is ineffective, since the common sub-sums are calculated many times. For example, the “naive” algorithm for calculating the beamlet transformation requires 0(n 3 ) operations, which is too much to use in real time and on mobile platforms. However, D.L Donoho and coauthors refuse to consider the issue of fast calculation of the beamlet transformation and assume such a result to be already known for a given image. At the same time, the authors list several studies aimed at fast calculation of the discrete Radon transformation, which is similar to the beamlet transformation. One of
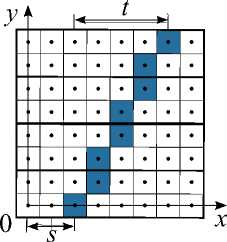
Fig. 1. The (s, t)-paramete-rization of a predominantly horizontal pattern with a downward slope (t > 0)
these approaches is the algorithm of Radon transformation. The algorithm P. Brady [3] and is also known as transformation (FHT) [4]. Nowadays, the was the the
fast discrete proposed by fast Hough algorithm is
studied in detail. In 0(n2 log n) operations, the algorithm allows to calculate accurately the total Hough-image (i.e. an image, each pixel of which contains the sum over the pattern, the parameters of which are usually given by the coordinates of this pixel) over the dyadic patterns (further, we refer to dyadic patterns as dyadic straight lines). The dyadic straight lines well approximate straight lines on the plane, since the approximation error along the ordinate axis is log62 n for straight lines with the slope k < 1 in the parametrization by an angular coefficient [5]. Moreover, it is proved that the asymptotic complexity of the FHT algorithm cannot be improved [6].
In the FHT algorithm, the sum over a dyadic pattern is composed of two sums over halves of the pattern, which are also dyadic patterns, while the sums over the halves are also composed of the sums over their halves, etc. Therefore, if intermediate results are saved during the process of calculating the FHT, then a FHT pyramid is formed, which is largely similar to a beamlet pyramid. Saving intermediate results does not increase asymptotic complexity of the FHT algorithm, therefore, the FHT pyramid can be constructed in ©(n2 log n) operations.
In this paper, we propose an algorithm for fast (in ©(log n) operations) finding of the sum over an arbitrary (given by a pair of points) segment of a dyadic pattern in an image. This algorithm is based on the FHT-pyramid and can be used as a method for calculating the fast beamlet transformation (approximation of the beamlet transformation summing over dyadic patterns). The asymptotic complexity of the fast beamlet transformation is Q(n 2 log 2 n) operations. The proposed algorithm is also of independent value in problems that require to calculate numerous sums over segments in an image, but do not require such a high-level theory as the beamlet analysis [7]. At the same time, if it is necessary to find only a summation over segments having a certain range of slope angles, then the volume of the pre-calculation can be reduced by performing a partial FHT and calculating the pyramid only for the partial FHT [8].
For three-dimensional images, two generalizations of the Radon transformation are known: the three-dimensional Radon transformation (summations over straight lines in the three-dimensional space) and the John transformation (summations over planes). For both generalizations, the algorithm for fast summation over dyadic patterns is known: the three-dimensional fast Hough transformation is used over straight lines and planes, respectively [9]. In this paper, we propose an algorithm for fast summation over segments of dyadic straight lines in a three-dimensional image and over segments of dyadic planes of a special type.
1. Fast Finding of the Sum Over an Arbitrary Segment
For brevity, we consider only square images of the size n x n pixels, where n = 2 p . Following the paper [9], we use the (s, t)-parameterization of straight lines in the image. To this end, first of all, we divide all the straight lines into two classes: predominantly vertical straight lines (i.e. vertical straight lines and straight lines with | k | > 1 in the parameterization by the angular coefficient) and predominantly horizontal straight lines (i.e. straight lines with | k | < 1). Therefore, we refer straight lines with k = 1,
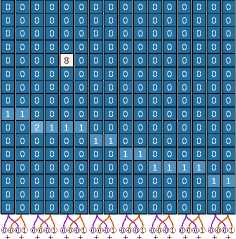

+ + ++ + + + + + + + + + + + +
+ + + + + + + +

+ + ++ + + + +
++++++++
0 0 0 0 0 0 0 0 0 0 0 0 0 1 10
0 0 0 0 0 0 0 0 0 0 8 8 9 10 1 1 0000008888022212

s
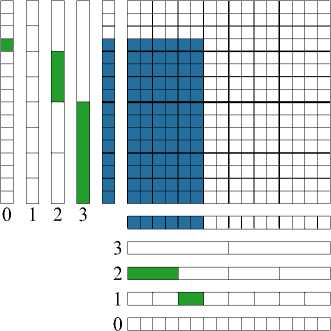
Fig. 2. FHT-pyramid for an image of the size 16 x 16
t
-
i.e. inclined at an angle 45 ° , to both classes. Note that the FHT for predominantly horizontal straight lines is also suitable for predominantly vertical ones. Indeed, it is enough to rotate the original image by 90 ° . Therefore, further we consider only predominantly horizontal straight lines. Such a straight line can be given by the parameters s and t of the coordinates of two points on the vertical boundaries of the image: (0, s) and (n — 1, s +t), where t E [ — n + 1; n — 1] and s E [ — n + 1; n — 1], see Fig. 1. For brevity, we consider only the case of t > 0, i.e. predominantly-horizontal patterns inclined downward and the Hough-image for such patterns.
A Hough-image is represented as an image of the size n x n, whose each point (s, t) contains the sum over the pattern with such parameters. In this paper, we are interested not only in the algorithm itself, but also in the intermediate results of the algorithm implementation, which can be represented as (log 2 n + 1) images (levels) of the size n x n forming a FHT-pyramid.
-
1.1. FHT-Pyramid
Taking into account the assumptions and the definitions given above, we describe the FHT-pyramid and the method of its calculation. The zero level of the FHT-pyramid is the original image, and the last level is the Hough-image containing sums over dyadic straight lines of the length n = 2 p . Similarly to the description of the beamlet pyramid level, we describe the q -th level of the FHT-pyramid. To this end, divide the original image into vertical stripes [k • 2 q , (k + 1) • 2 q — 1] x [0, n — 1], where k denotes the number of the stripe, k E [0, 2 p - q — 1]. For each stripe, the q-th level of the FHT-pyramid contains the sums over all possible patterns of the stripe that have the length 2 q and the parameters s E [0 , n — 1] and t E [0, 2 q — 1]. The number of such patterns is equal to n x 2 q for each strip. Therefore, the q -th level of the FHT-pyramid requires as much memory as the original image. Fig. 2 shows an example of the algorithm implementation and the formation of all levels of the FHT-pyramid.
-
1.2. Finding of the Sum Over a Segment of a Known Dyadic Straight Line
Consider a fast way to calculate the sum over any segment in the image using the FHT-pyramid [10].
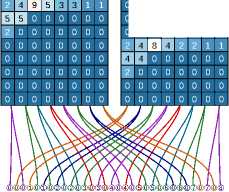
Suppose that it is necessary to find the sum over the segment B'C of a predominantly horizontal inclined downward dyadic straight line AD, whose parameters (s,t) are known. Let us find the sum as the difference between the sums over the segments AC and AB .
Denote the length of the segment AB by l . Let us find the sum over AB as the sum of the minimum number of already calculated sums saved in the FHT-pyramid, see Fig. 3.
Suppose that the binary expansion of the length of AB has the form l = J2p = 0 l j 2 j . Then the sum over the segment AB is calculated by the formula
pp
ss,t(i) = E [i« • hs,t (q, E i> • 2j-'), q=0 j=q+i where Hs,t(q, k) denotes the sum over the pattern of the length 2q in the k-th stripe of the q-th level of the FHT-pyramid for a straight line with the parameters (s, t).
The internal sum does not require a complete calculation at each step, since the sum is obtained from the previous one in constant time. Therefore, the complexity of the algorithm is proportional to the number of terms in the external sum, i.e. is equal to ©(logn). Similarly, the sum over the segment AC is calculated.
For the case of dyadic straight lines in a three-dimensional image, note that the described algorithm for finding of the sums is almost identical, except that the search is performed in a four-dimensional FHT-pyramid, which does not affect the complexity of the search due to dyadic organization of the FHT-pyramid.
-
1.3. Finding of a Dyadic Pattern
The paper [9] proves that at least one dyadic pattern passes through any two pixels, but such a pattern can

between the sums over the segments AC and AB
be not unique. Let us solve the problem on finding of the parameters (s, t) of any one of the patterns passing through the given points (x1,y1) and (x2,y2). Without loss of generality, we assume that x2 ≥ x1 . Since, as stated above, we consider only predominantly horizontal patterns inclined downwards, then y2 ≥ y1 and y2 - y1 ≤ x2 - x1 .
Suppose that the binary expansion of the parameter t of the desired pattern has the form t = £ p =(1 t i 2 i . Then the pattern can be given by the following equation [5]:
p - 1
y = Ds,(x) = s + £tr r=0
2 r x
2 p - 1
where [ • ] denotes rounding to the nearest integer. Expression (1) shows that translation of any dyadic pattern can be represented as the sum of subset translations of the basic dyadic patterns of the form
2 r x
2 p - 1
D r (x) =
Substitute the coordinates of the points (x1, y1) and (x2, y2) into expression (1) for the pattern and subtract the second equation from the first one:
p - 1
У 2 — У 1 = Ds, t (x2) - Ds,t(x i ) = ^ t r (D r (X 2 ) - D r (x i )).
r =0
Denote Ay = y2 — y1. Let S^'x = Di(x2) — Di(x1) be the number of shifts of the i-th basic dyadic pattern in the stripe (x1 , x2), then the equation takes the form p-1
Ay = £t r S r ^ x2 .
r =0
Therefore, the problem on finding of a slope is reduced to the following problem: to restore the bits t 0 , t 1 , ..., t p - 1 for the known Ay and S 0 1 'x 2 , S f 1^2 , ..., S p -Ap2 .
To this end, apply the “greedy” algorithm. First, consider all ti to be zero. Since δix1,x2 ≥ δjx1,x2 for i > j, we go through shifts from the large number to less one, that is, go from the larger level to zero one. If Ay > jx^x2, then consider ti to be equal to 1 and reduce Ay by jx^’x2. Repeat the procedure until Ay is not equal to zero (we prove that Ay = 0 at some moment, i.e. that the algorithm is correct, below).
Use the value of the parameter t to find the parameter s of the dyadic pattern as p-1
s = D(x 1 ,t) — ^^t r D r (x 1 ).
r =0
Since # { ^ X 1 ’x 2 } = P = l°g 2 n, then the complexity of the algorithm is ©(logn) operations.
-
1.3.1. Correctness of the Algorithm
Theorem 1.
D
j
(x)
—
1
<
^2 D
i
(x)
<
D
j
(x)
V
x
G
0,n
—
1
and
V
j
G
0,p
—
1
.
i
Proof. For j G 0,p — 1, consider the sets J j formed by the coordinates of the shift pixels of the basis dyadic pattern with slopes 2 j , i.e. those for which the ordinate is greater than the ordinate of the previous one: D j (x) = D j (x — 1) + 1.
Since |Jj+1| = 2|Jj |, then, similar to a binary tree, where the number of leaves is greater by unity than the number of other nodes, we obtain that Jj = ^ Ji + 1. According i From the properties given ab ove, it follows that the shift pixels of the set Jj alternate with the shift pixels of all other sets Ji (for i < j), and the first shift pixel belongs to the set Jj . Therefore, Vx G [0,n — 1], the number of boundary pixels of Dj(x) is either equal to or greater by unity than Di(x). i □ Corollary 1. £ jx-1^ — 1 < 6j1X2 < £ Jx-1^ +1 i Vj G 0,p — 1 and Vx1 ,x2G [0, n — 1] such that x1 > x2. Proof. Rewrite Theorem 1 as ^2 Di (x) < Dj (x) < Dix) (x) + 1. Apply this pair of i □ Theorem 2. If the numbers δ0x1,x2 , δ1x1,x2 , ..., δkx1,x2 satisfy condition (3), then the sums of subset translations of their every possible subsets cover the range of values from 0 to k i=0 δix1,x2 Proof. Let us prove by induction. First, we show that the statement is true for i = 0. Formula (2) implies that 5X1’X2 = [П—у] — [П—у] > 0, since x2> x1 by condition, i.e. 0 < C’x2< 1. Second, suppose that the statement is true for i = k — 1, that is, we can obtain all k-1 sums from 0 to V Sx1’x2 for the given numbers 5^1,x'2,SX1,x2,..., 5X1,X2. i 0 1 k-1 i=0 Finally, show that the statement is true for i = k. Inequality (3) is satisfied for 5X1,X2. k-1 In other words, the difference between δkx1,x2 and δix1,x2 is no more than 1. Therefore, i=0 we can add δkx1,x2 to every possible sum of the numbers δ0x1,x2 , δ1x1,x2 , ..., δkx-1,1x2 to obtain all k sums from 0 to δix1,x2 . This completes the proof. i=0 □ p-1 Therefore, if Ay < £ sX1,x2 , then there exists a dyadic pattern passing through two i=0 given pixels. Theorem 3. The proposed algorithm to find a dyadic pattern always converges to a solution. Proof. Since we go through 5X1,X2 from k = p — 1 to k = 0, then inequality (3) is satisfied forallδx1,x2,δx1,x2...δx1,x2 at each stage, therefore, Theorem 2 is true for δx1,x2, δx1,x2...δx1,x2. 0 1 k-1 0 1 k-1 Hence, the problem has a solution at each stage. Therefore, we always obtain a solution to the problem. □ The proposed algorithm and its properties are directly generalized to the case of straight lines in large dimensions. To this end, it is enough to solve the problem for projections of a straight line of the length n on the coordinate planes sequentially.
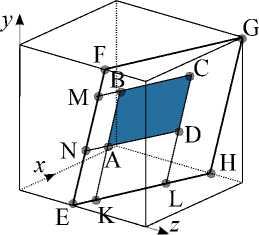
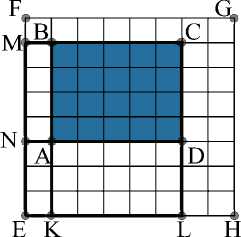
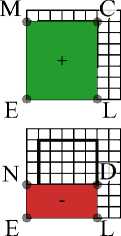
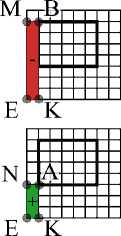
2. Fast Finding of the Sum Over a Segment of a Plane Following the paper [9], we introduce the typification of planes in a three-dimensional image. A plane is said to be predominantly perpendicular to a coordinate axis, if an angle between the normal to the plane and this coordinate axis is smaller than each of angles between the normal and other coordinate axis. We consider only the planes that are predominantly perpendicular to the coordinate axis OX . Such planes are divided into four types depending on the slopes, see Fig. 4. Without loss of generality, we assume that the considered planes are of the type I. Fig. 4. Typification of planes in the space given in the paper [9] Let EFGH be a dyadic plane in which it is necessary to find the sum over a segment. Similarly to the previous section, we consider the parameters (s,t1,t2) of the dyadic plane EFGH to be already found. As the segments, we consider the parallelograms, whose sides are parallel to the faces of the image. For example, see the parallelogram ABCD in Fig. 5. Let us briefly describe the procedure of pre-calculation. According to the paper [9], the algorithm of a three-dimensional FHT for planes is as follows. First, apply a twodimensional FHT to each horizontal layer of a three-dimensional image (such an operation is called the horizontal FHT). Then, in the resulting image, apply a FHT to each vertical Fig. 5. The dyadic plane EFGH containing the segment ABCD, and their projections to the coordinate plane OY X plane (such an operation is called the vertical FHT). In order to construct a threedimensional FHT pyramid, we apply the vertical FHT (and save all intermediate values) to the two-dimensional FHT pyramids constructed in the process of applying the horizontal FHT to each horizontal layer. In other words, the three-dimensional FHT pyramid contains the sums over all rectangles of the form 2l x 2m from the dyadic division of the Donoho-type plane. Since the vertical FHT is applied to n log2(n) planes, and the complexity of the twodimensional FHT is ©(n2log n), then the described calculation of the three-dimensional FHT pyramid has the complexity Q(n3 log2n). The sum over the segment ABCD can be calculated by the inclusion-exclusion formula SABCD = SEMCL—SEMBK—SENDL + SENAK • Note that the point E is one of the angles for each segment. Further, we refer to such segments as the angle segments. Consider the angle segment EMCL. It is necessary to divide EMCL into the segments presented in the FHT pyramid. Consider binary expansions of the width and height of a segment. Similarly to the one-dimensional case, divide the segment horizontally into log2n vertical stripes and vertically into at most log2n horizontal stripes. Intersection of these stripes contains no more than log2(n) segments presented in the three-dimensional FHT pyramid, see Fig. 6. Therefore, the complexity of calculating the sum over an arbitrary segment is ©(log2n) operations. Fig. 6. Algorithm to find a segment of a plane taking into account the previously calculated three-dimensional FHT pyramid Discussions The algorithms similar to FHT have an important practical property: in order to calculate such an algorithm, it is enough to use the addition operation only. This fact is essential for the calculation complexity. Algorithms having good computational characteristics are especially in demand to create modern neural network detectors. For example, the paper [11] proposes an effective method to find the vanishing point of an image using a convolutional neural network containing FHT layers capable to detect straight lines in the image. In the paper [11], the use of FHT allows to reduce significantly the size of the neural network under the same quality of detection. By analogy, we can assume that, in the problems on detection of segments of the image, effective convolutional neural networks include layers that calculate the FHT pyramid. Also, the developed solutions can be useful to create computer vision systems based on the algorithms of segment detection, for example, in combination with the methods proposed by D.L. Donoho and coauthors. On the other hand, a number of nontrivial and interesting mathematical problems arise when the FHT is generalized to the cases of higher dimensions. In particular, the existence of a dyadic plane passing through any three given voxels is not proved yet, to say nothing of generalizations of these statements to the cases of higher dimensions. The study and development of the algorithms similar to FHT has good potential both for use in various image-based systems of navigation and localization and for new mathematical problems. Conclusion In this paper, we present an algorithm for the fast search for segments of straight lines and segments of planes in the two-dimensional and three-dimensional cases using the corresponding fast Hough transformation as a pre-calculation. Also, we propose a method to find the parameters of a dyadic straight line passing through arbitrary two pixels of an image. In order to continue the development of this work, we plan to study the issue of proving the theorem that at least one dyadic plane passes through any three voxels, as well as to investigate the possibility to calculate fast the sum over an arbitrary triangular segment in a three-dimensional image. Acknowledgments. The team of authors is grateful to A.P. Terekhin for his help in preparing wonderful illustrations for this paper, as well as to A.V. Savchik for valuable advices on how to simplify the proof of Theorems.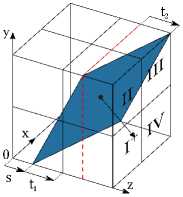
Список литературы Acceleration of summation over segments using the fast Hough transformation pyramid
- Donoho, D.L. Beamlets and Multiscale Image Analysis / D.L. Donoho, Xiaoming Huo. - Berlin: Springer, 2002.
- Arias-Castro, E. Near-Optimal Detection of Geometric Objects by Fast Multiscale Methods / E. Arias-Castro, D.L. Donoho, Xiaoming Huo // IEEE Transactions on Information Theory. - 2005. - Т. 51, № 7. - С. 2402-2425.
- Brady, M.L. Fast Parallel Discrete Approximation Algorithms for the Radon Transform / M.L. Brady, Whanki Yong // Proceedings of the Fourth Annual ACM Symposium on Parallel Algorithms and Architectures. - 1992. - C. 91-99.
- Nikolaev, D.P. Hough Transformation: Underestimated Tool in the Computer Vision Field / D.P. Nikolaev, S.M. Karpenko, I.P. Nikolaev, P.P. Nikolaev // Proceedings of the 22th European Conference on Modelling and Simulation, 3-6 June. - Nicosia, 2008. - T. 238. - C. 246
- Ershov, E.I Hough Transform and Approximation Properties of Dyadic Patterns / E.I. Ershov, S.M. Karpenko. - 2017. - URL: https://arxiv.1712.05615
- Khanipov, T.M. Computational Complexity Lower Bounds of Certain Discrete Radon Transform Approximations / T.M. Khanipov. - 2018. - URL: https://arxiv.801.01054
- Skoryukina, N. Document Localization Algorithms Based on Feature Points and Straight Lines / N. Skoryukina, J. Shemyakina, V.L. Arlazarov, I. Faradzhev // The Tenth International Conference on Machine Vision. - 2018. - V. 10696. - P. 106961H.
- Aliev, M. On the Use of FHT, Its Modification for Practical Applications and the Structure of Hough Image / M. Aliev, E.I. Ershov, D.P. Nikolaev // International Society for Optics and Photonics. - 2019. - V. 11041. - P. 1104119.
- Ершов, Е.И. Обобщение быстрого преобразования Хафа для трехмерных изображений / Е.И. Ершов, А.П. Терехин, Д.П. Николаев // Информационные процессы. - 2017. - Т. 17, № 4. - С. 294-308.
- Сошин, К.В. О быстром поиске сумм по сегментам за счет предподсчета Хаф-пирамид / К.В. Сошин, С.А. Гладилин, Е.И. Ершов // 43 Междисциплинарная школа-конференция ИППИ РАН технологии и системы. - Пермь, 2019.
- Sheshkus, A. Vanishing Points Detection Using Combination of Fast Hough Transform and Deep Learning / A. Sheshkus, A. Ingacheva, D. Nikolaev // International Society for Optics and Photonics. - 2018. - V. 10696. - C. 106960.
- Арлазаров, В.Л. Об экономном построении транзитивного замыкания ориентированного графа / В.Л. Арлазаров, Е.А. Диниц, М.А. Кронрод, И.А. Фараджев // Доклады Академии наук СССР. - 1970. - Т. 194, № 3. - C. 487-488.


