Адаптивное матричное представление информации о параметрах для взаимодействующих автономных интеллектуальных систем

DOI:

Проблема функционирования автономных интеллектуальных систем (АИС) является одной из самых распространенных, возникающих при проектировании различных технических объектов [1-3], информационных систем [4-6], автономных (беспилотных) летательных аппаратов и комплексов [7-11].

Характер представления информации о внешнем мире и о состоянии самой автономной системы определяет дальнейшую возможность расширения области применения АИС. Внутреннее представление информации в АИС, ориентированных на взаимодействие, отличается от такового в обычных системах, так как необходимо обеспечить работу механизмов обмена информацией [12].

Представление информации о параметрах, не имеет смысла без информации об объектах и процессах. Каждый параметр относится к какому-либо объекту или процессу, и описывает его состояние. Именно разработке представления и обработки информации в АИС, ориентированной на взаимодействие, посвящена настоящая статья. Отправной точкой описания параметров в качестве объектов возьмем сами АИС. Хотя в общем случае параметры описывают более широкий набор понятий [13].

МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ

Имеется некоторая совокупность автономных интеллектуальных систем [14-16], которую будем обозначать следующим образом:

A s = { S , , S , ,..., S n } .

Каждая АИС S характеризуется некоторыми параметрами, причем набор параметров может быть как общим для группы систем, так и индивидуальным для каждой автономной системы, либо представлять собой комбинацию из общих и уникальных параметров.

Список параметров системы представим в следующем виде:

F PSar = { Par iS , Part ,-, Par t } .

Для каждого параметра имеется дополнительная информация – это описание. Для систем, оперирующих с данными из реального мира, или его модели, это описание того, чем является этот параметр физически, то есть, обозначим: par = { parf, I_s } .

Имеется матрица зависимости каждого параметра от других параметров системы, от параметров других систем, и от истории значений этого параметра, а также параметров других систем. Данную матрицу представим следующим образом:

'Va/par, /va^ val1  ,„ Par, val2 ,„    • par, • val1  ,„ Par M (parout) — val1  , Par val1,1 „„, pariout valpa'r ' ■■    val1’ lo„, pariout val , pari val2,1 o„, par val 22 out   ■ par ■ •    val ’ o„, par ,                               (1) k k val  n <        par valk11 o„t pariout valk,2 o„,    ■ pariout valk ’ lo„, par 7 где parOut — parS .

В таком случае скорость изменения параметра par^S выражается как параметр par’' S . Это скорость изменения параметра, которую можно представить в виде:

SS par - par       S

S - t      t—At - APari par.  ^              —        , t — (t — At)      At причем t – также является параметром «время», т.е. скорость изменения любого параметра можно представить в виде зависимости от величины изменения параметра и времени выполнения этого процесса.

Очевидно, что любую зависимость параметра, можно свести к матрице зависимости необходимой размерности с необходимым количеством значений параметров.

Введем следующие определения.

• •    Входной параметр матрицы зависимости - тот параметр, от которого зависит рассматриваемый параметр.

• •    Выходной параметр матрицы зависимости - тот параметр, который зависит, он, как правило, является рассматриваемым параметром. Значения такого параметра находятся на пересечении значений входных параметров.

В общем случае временная характеристика t сама является неким параметром функционирования систем. Однако для адаптации полученной математической модели хранения информации к прикладному применению введем понятия истории значения параметра и изменения параметра.

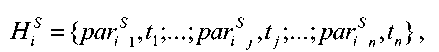
где

• •    parf j - значение параметра на определенную отметку времени t_},

• •    п - количество значений параметра в сохраненной истории.

Изменение параметра само является параметром, например изменение параметра во времени - это параметр «скорость изменения» par/5 = Aparj5 = par? — par?, а t       t-At

история значения – это конкретные значения параметра на конкретную отметку времени j : par ? = par ?. , p^{ar f}+i = t .

Вводя в матрицу зависимости истории значения параметра, в ней появляются два параметра: отметка времени (причем она может быть абсолютной, а может быть просто сдвигом во времени), и значение параметра. В общем случае получаем добавление к матрице зависимости дополнительной зависимости от двух параметров (отметка времени и значение параметра). В математической записи следует различать записи абсолютного значения отметки времени и относительного сдвига, но при программировании автономной системы, можно воспользоваться различной типизацией этих переменных и таким образом по типу переменной можно сделать вывод о характере сдвига отметки времени.

H =V  ,val1- m} pari       1...m,      pari

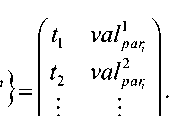
val ¹

Par i val^г par _i

val ⁴

par i /

В результате, получаем матрицу зависимости параметра (1). Количество измерений соответствует количеству учтенных входных параметров, а на пересечении значений входных параметров стоит значение выходного параметра.

ЗАПОЛНЕНИЕ МАТРИЦЫ ЗАВИСИМОСТИ ИНФОРМАЦИЕЙ

Для того чтобы обеспечить процесс сбора и анализа информации о параметрах, необходимо разработать механизм заполнения матриц зависимости информацией. Заполнение матриц зависимости происходит в ходе анализа изменения других параметров.

При п параметрах, получаем, если min( A p ) ^ max( A p°^ut ), то от такого параметра j = 1, n

Pj зависит выходной параметр Ptut. Если каждый раз при одинаковых значениях pj, min(Apj) ^ max(Ap°ut), причем siyn(Apj) = si_gn(Ap°ut), то примем что параметр pfut j =1, n некоторым образом зависит от параметра p . Характер зависимости можно выявить, только получив некоторое количество экспериментальных данных, достаточных для заполнения матрицы зависимости по новому измерению.

Однако некоторые зависимости могут быть гораздо сложнее и обнаружить их описанным способом невозможно. Для этого необходимо контролировать изменение совокупности параметров, причем независимо от знака изменения, так как в ряде случаев, только разнознаковое изменение двух параметров приводит к изменению выходного параметра (например, в переключателях).

Добавление входного параметра в матрицу зависимости

Если при регистрации изменения параметра обнаруживается, что известные входные параметры не изменялись, то это значит, что выходной параметр зависит от одного или множества неизвестных параметров. Выполняется поиск того параметра, который влиял на значение выходного параметра. Происходит анализ изменений параметров и берется тот параметр, при минимальном изменении которого максимально изменился выходной параметр.

Если однозначно идентифицировать зависимость только от одного параметра не удается даже в ходе специальных экспериментов, то происходит добавление сразу нескольких изменившихся параметров. Однако, как правило, всегда можно выделить параметр, который оказал наибольшее влияние на значение выходного параметра.

Удаление входного параметра из матрицы зависимости

Добавлять параметры в матрицу зависимости можно сразу все, а затем проводить отбор, путем исключения несущественных параметров, в первую очередь тех, при значительном изменении которых выходной параметр не изменился. Затем тех, при незначительном изменении которых выходной параметр не изменился. Затем происходит удаление несущественных параметров, от которых выходной параметр изменяется, но не стабильно, и/или незначительно, т.е. меньше порогового значения точности изменения параметра.

Однако в случае, если в матрице зависимости будет очень большое количество параметров, такая матрица будет слишком большой, время её обработки будет слишком велико, чтобы говорить об эффективной обработке информации.

Процесс исключения параметров из матрицы, содержащей все параметры, как и процесс добавления параметров в матрицу, не содержащую ни одного параметра в конечном итоге, должен привести к одному и тому же набору параметров, вплоть до того, что матрицы зависимости могут стать идентичными.

Однако процесс заполнения, удаления и корректировки входных и выходных параметров в матрице зависимости никогда не заканчивается. Происходит непрерывное обучение АИС, процесс добавления и исключения параметров взаимодополняем.

ВЕРОЯТНОСТНОЕ РАСПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ВЫХОДНОГО ПАРАМЕТРА В МАТРИЦЕ ЗАВИСИМОСТИ

Вообще в совокупности матрица зависимости выходного параметра от входных заполняется на основе статистических данных, полученных в ходе обучения, самообучения, работы, то есть данных, полученных экспериментальным путем.

Таким образом, значение выходного параметра на пересечении значений входных, это математическое ожидание значения выходного параметра. Такая статистическая информация несет с собой неточность и невозможность точного и однозначного определения выходного параметра.

Для того чтобы представить информацию в матрице в наиболее точном виде, при всей имеющейся входной информации, введем понятия максимального отклонения значения выходного параметра.

Эта дополнительная информация будет представлять собой два дополнительных значения выходного параметра, к каждому имеющемуся, и будет отражать минимальное и максимальное возможное значения выходного параметра, полученное экспериментальным путем, четкая зависимость которого еще не найдена.

S par _i ^S

n

Е (parS) n min( par^S), max( parS ), —------- n

г ,

где n - количество полученных значений параметра экспериментальным путем.

В ходе дальнейших действий по обучению АИС, или в ходе выполнения задач, может возникнуть ситуация, когда будет обнаружен входной параметр, от которого как раз зависит значение выходного параметра, и эта зависимость может быть четко определена (т.е. всегда можно получить значения такого входного параметра). И этот входной параметр будет добавлен в матрицу зависимости. Однако пока такая зависимость не обнаружена, необходимо учитывать возможные максимальные отклонения выходного параметра для того, чтобы в ходе решения задач учитывались возможные отклонения значений параметра.

Плотность распределения вероятности для значений параметра

Для большого числа случаев обнаруживаемой зависимости необходимо отразить не только минимальной и максимальное значение выходного параметра, но и характер распределения вероятности значения выходного параметра, для каждого сочетания значений входных параметров.

Обнаружение такой зависимости возможно лишь при достаточном количестве полученных фактических данных о значении выходного параметра, построение такой зависимости целесообразно только для параметров, время вычисления значения которых, некритично, а сами параметры выражают характеристики объектов, работа над которыми длится некоторое время, большее, чем требуется для проведения вычислений.

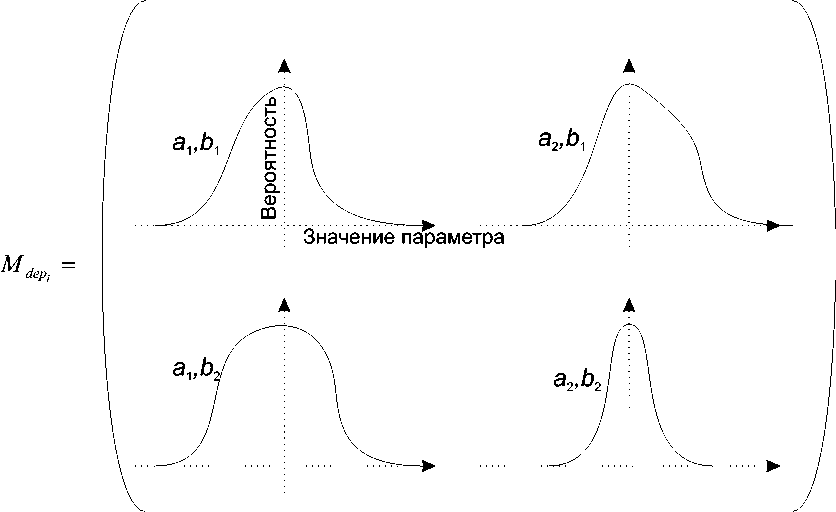
Рисунок 1. Плотности распределения вероятности значения выходного параметра в зависимости от комбинации значений двух входных параметров.

Figure 1. Probability densities of the output parameter value depending on the combination of the values of two input parameters.

Характер распределения вероятности целесообразно представить также в виде матрицы зависимости вероятности значения параметра, от значения этого параметра.

	veil 1 par	va11, '
V dep i =	va^ p ar ,	val v	,				(5)
	. va 1^	val k^
		val Ival par ,       par ^		va1 pa r2	val par ,   •	■■   val‘par2 '
		val	1 par ,	V I,1 dep	V 1-2 dep	!' 1 V dep
тогда M dep_ =		val	2 par ,	V2Л dep	V22 dep	2,1 V dep	.                                   (6)
		val V	k par ,	уk -1 dep	k,2 dep	k,1 dep i  у

В таком виде даже простое описание минимального и максимального значений параметра можно описать в виде матрицы распределения вероятности:

V dep i

'min par®) £ (Par?) n -=H n max( par® )

val,

val2,

val3,

к                  7

ЗАКЛЮЧЕНИЕ

Таким образом, нами разработано матричное представление информации о параметрах для взаимодействующих автономных интеллектуальных систем. Данное представление формализует зависимости каждого параметра от других параметров системы, от параметров других систем, от истории значений этого параметра, а также параметров других систем.

Разработанный механизм заполнения матриц зависимости информацией осуществляется с учетом анализа изменения других параметров. Он включает как этап добавление входного параметра в матрицу зависимости, так и этап удаления входного параметра из матрицы зависимости. Отметим, что процесс заполнения, удаления и корректировки входных и выходных параметров в матрице зависимости никогда не заканчивается в процессе взаимодействия АИС, так как происходит непрерывное обучение АИС. При этом процесс добавления и исключения параметров взаимодополняем. Так как матрица зависимости выходного параметра от входных заполняется на основе статистических данных, полученных в ходе обучения, самообучения, работы, то есть данных, полученных экспериментальным путем, то в работе рассмотрено вероятностное распределение значений выходного параметра в матрице зависимости.

В качестве примера представлены плотности распределения вероятности значения выходного параметра в зависимости от комбинации значений двух входных параметров. Такой характер представления информации направлен на повышение эффективности функционирования автономных интеллектуальных систем и дальнейшую возможность расширения области применения АИС.