Актуальные проблемы глобальной модернизации радиоэлектронных средств обнаружения

В современной теории помехоустойчивого приема сигналов фундаментальная система решений проблемы обнаружения сигналов определена выбором базиса [1] гильбертова пространства. В этом пространстве в качестве критерия верности, на основе которого оценивается уклонение выходного сигнала s ( t ) от принятого сообщения x ( t ) применяется критерий квадратичного уклонения.

Для непрерывных функций, заданных на интервале ( a , b ), квадратичное уклонение выражается соотношением

b s2 =J[ x (t) - s (t )]2d t,                 (1)

a что соответствует норме гильбертова пространства:

II / II -.jib [ f ( t )]²d t .                   (2)

С точки зрения геометрических представлений уклонение s есть не что иное, как расстояние а ( x , s ), а выбор критерия — это выбор метрики пространства сообщений [2].

Проблема заключается в том, что для решения поставленной задачи выбор критерия квадратичного уклонения отнюдь не является оптимальным. Несовершенство этого процесса может быть подтверждено следующими установленными фактами.

• 1)    Если норму пространства Гильберта (2) ввести в совокупность всех непрерывных функций на конечном интервале a <  t <  b , то хотя все аксиомы линейного пространства и нормы выполнены, но такое пространство не будет полным , т. к. предел функций может быть разрывной функцией, что влечет за собой существенные трудности при необходимости получить состоятельные оценки статистических характеристик при статистическом анализе [3].

• 2)    Из множества статистических характеристик исключают все нечетные моменты, что существенно сокращает и обедняет информационное поле. Так, например, все детерминированные процессы, имеющие одинаковый амплитудный спектр (модуль) и различные фазовые спектры, обладают одинаковыми временными, корреляционными функциями и энергетическими спектрами, что существенно затрудняет обнаружение целей, особенно в случае их прикрытия средствами имитации и при помехах типа ангел-эхо [4].

• 3)    При слабом (относительно помехи) сигнале в квадратичном и линейном детекторах имеет место подавление сигнала. Анализ показывает, что это свойство присуще детекторам и с любыми другими вольтамперными характеристиками [5]. Данное обстоятельство накладывает существенное ограничение на увеличение дальности действия всех без исключения радиоэлектронных средств наблюдения и связи.

АЛЬТЕРНАТИВНЫЙ ПОДХОД

Все перечисленные выше недостатки есть следствие неоптимально выбранного критерия, на основе которого принимается решение о правильности приема сигналов. В то же время "нет решительно никаких общих оснований для предпочтения одного критерия другому. Критерий квадратичного уклонения особенно часто применяется только потому, что при пользовании этим критерием получаются, как правило, сравнительно простые выкладки" [2].

Однако с момента создания теории потенциальной помехоустойчивости В.А. Котельникова прошло уже более 70 лет. За это время математика как наука и вычислительная техника получили свое существенное развитие в работах С. Банаха, Дж. Дуба, А.Н. Колмогорова и других, что позволяет решать задачи оптимального приема на основе всего известного множества критериев. Каждому из этих критериев соответствует некоторое пространство функций, заданных на интервале [ a , b ] и обладающих определенными свойствами. Так, например, множеству радикально-интегральных критериев L_n , для которых величина уклонения функций определяется в соответствии с выражением [1]

b

• ^s r =ji f ( t )i p d t ,

a

соответствует пространство L p [ a , b ] — пространство функций x = f ( t ), определенных на [ a , b ] с нормой

( bV

IIм = jif(t)p dt.

V a/

Однако данный вид пространств обладает тем же комплексом недостатков, что и пространство Гильберта. Если учесть, что качество приема, как правило, определяется отношением сигнал/помеха на выходе приемника, т. е. отношением приращения постоянной составляющей, обусловленное наличием сигнала, к среднеквадратическому отклонению флуктуаций на выходе приемника или на входе решающего устройства, тогда наибольший интерес должны представлять пространства, обеспечивающие максимум этого приращения при минимуме флуктуаций на выходе приемника.

С этой точки зрения наибольший интерес представляют пространства, основанные на использовании критерия наибольшего уклонения:

странств, которые принято называть банаховыми пространствами. К таким относятся следующие пространства.

• 1)    Пространство C [ a , b ] функций, заданных и непрерывных при a <  t <  b , с нормой

II f l 1 = ^maxl f ^{( X} )|. ⁽⁶⁾ a <  t <  b

• 2)    Пространство C 1 [ a , b ] функций, заданных и непрерывных при a <  t <  b вместе со своей производной, с нормой

II f l I = ^max I f ^{( X} )l + ^max I f '( ^X )l. (7) a < t < b a < t < b

• 3)    Пространство C 2 [ a , b ] функций, заданных и непрерывных при a <  t <  b вместе со своей первой и второй производными, с нормой

II f l I = ^max I f ^{( X} )l + ^max I f ^{,( X} )l + ^max I f "^{( X} )l ⁽⁸⁾ a <  t <  b' a <  t <  b' a <  t <  b'

и т. д.

Так, например, пространство C n [ a , b ] — пространство функций, заданных и непрерывных при a <  t <  b вместе со своими n производными, с нормой

n

II f l 1= Ё m a b l ^f/ ( ^{X )}^ ⁽⁹⁾ i = 1

В качестве нормы в C n [ a , b ] можно взять также не сумму, а наибольшее из слагаемых, стоящих в правой части [3].

Количество слагаемых в (9), т. е. число n , следует определять в концепции наилучшего приближения. С этой точки зрения и сигналы, и помехи являются некоторым множеством колебательных движений и, как для всякого другого вида движения, для их полной характеристики необходимо знать скорость и ускорение, т. е. первую и вторую производные на участке пути [ a , b ]. Таким образом, и сигналы, и помехи могут быть описаны в функциональном пространстве C 2 [ a , b ] с нормой (8).

Пространство C 2 [ a , b ] является линейным нормированным полным пространством или коротко называется банаховым пространством. Одним из преимуществ данного вида пространств является возможность решения задач обнаружения, распознавания образов и измерения координат на виртуальном уровне, т. е. на уровне бесконечно малых приращений, тенденций и возможных направлений развития процесса.

Учитывая случайный характер сигналов, помех и их смеси, наиболее полной в вероятностном смысле их характеристикой является функция распределения, которая может быть однозначно представлена в виде суммы

F ( x ) = a 1 F 1 ( x ) + a 2 F 2 ( x ) + a 3 F 3 ( x ), (10)

где a 1 , a 2 , a 3 — неотрицательные числа, сумма которых равна 1, а F 1, F 2, F 3 — функции распределения, такие что F 1 ( x ) абсолютно непрерывна

F 1 ( x ) = j ^ ( t )d x , (11)

-to

F ₂( x ) — ступенчатая функция

F2( x) = E Pk, (12) x < x где xk — точки скачков F2(x), а Pk > 0 пропорциональны размеру этих скачков; F3(x) — сингулярная компонента, производная которой почти всюду равна нулю.

Очевидно, что в классической теории потенциальной помехоустойчивости значению функций F 2 ( x ) и F 3 ( x ) внимание практически не уделяется. Между тем понятие сингулярной (главной) части ряда Лорана было введено для обозначения части ряда Лорана с отрицательными степенями. А.Н. Колмогоров (1942 г.) доказал, что любой стационарный процесс может быть представлен в виде суммы регулярной (правильной) и сингулярной (главной) составляющих [6]. Далее Дж. Дуб доказал, что и регулярный стационарный случайный процесс может быть также однозначно разложен на регулярную и сингулярную составляющие. При этом под сингулярным процессом понимается вполне детерминированный процесс, параметры которого неизвестны. Однако, зная прошлое такого процесса, можно экстраполировать его значения на любой момент будущего с вероятностью единица .

Следует отметить, что еще в 1926 г. Е.Е. Слуцким была доказана предельная синусоидальная теорема, согласно которой под воздействием множества случайных причин при весьма общих условиях возникают вполне детерминированные синусоидальные процессы. Данную теорему следует считать фундаментальной при развитии теории самоорганизации. Несколько позднее В. Романовский доказал сложную предельную синусоидальную теорему, согласно которой под воздействием случайных причин могут возникать вполне детерминированные процессы любой степени сложности. Зная отрезок прошлого этих процессов, можно экстраполировать их значения на любой момент прошлого или будущего с вероятностью единица.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СМЕСИ СИГНАЛ+ПОМЕХА

Рассмотрим в качестве математической модели смеси сигнал+помеха сумму стационарного центрированного гауссовского процесса и гармониче- ского сигнала

X ( t ) = J X ( t ) + U cos to₀1 ,                (13)

o где X(t) — центрированный стационарный гауссовский процесс, U и ω0 — некоторые постоянные величины. Этот случай нередко встречается на практике, в частности в радиолокации и радиосвязи, когда U cos ω0t представляет регулярный сиг-o нал, а X(t) — флуктуационный шум. Заметим, что X(t) — нестационарный процесс, т. к. его математическое ожидание U cos ω0t зависит от времени [7].

В связи с последним замечанием возникает вопрос о погрешностях, к которым приводит предположение о том, что смесь на входе приемника представляет собой стационарный гауссовский эргодический процесс. В соответствии с концепцией Пуанкаре, такое допущение может привести к абсолютно неправильным выводам, что и подтверждается практическими исследованиями, когда увеличение длительности сигнала и времени накопления не приводит к решению задачи обнаружения слабых сигналов (т. е. таких сигналов, для которых отношение сигнал/помеха существенно меньше единицы).

Анализируя подобную ситуацию, А.А. Хар-кевич пишет [2], что "для получения осмысленных результатов нужно после усреднения по множеству прибегать к повторному усреднению по времени", иначе говоря, в современной трактовке необходимо переходить к скользящему групповому накоплению.

Для того чтобы реализовать накопление по множеству, следует рассматривать процесс, действующий на входе приемной системы, как единый колебательный процесс, который с физической точки зрения можно трактовать как последовательность (множество, ансамбль) колебательных циклов, т. е. переходы из одной точки устойчивого равновесия (точки минимума потенциальной энергии) в другую точку минимума. В этом случае с точки зрения актуальной бесконечности в качестве интервала [ a , b ] на временнóй оси может быть задан интервал 2 π , т. е. интервал между двумя соседними точками минимума.

Отметим, что все функции, составляющие функциональное пространство, должны быть заданы на одном и том же интервале. В противном случае их нельзя было бы складывать друг с другом [3].

При этом число n в норме (9) по существу определяется порядком дифференциального уравнения, описывающего данный вид колебательного движения. Современные исследования показывают, что уже в первом приближении колебательное движение лампового генератора описывается уравнением Ван-дер-Поля [8] вида d2y / dt2 + ω2y + µ f(y1 dy / dt ) = 0, (14) где µ — малая постоянная, т. к. последний член представляет малое нелинейное возмущение. Решение этого уравнения ищут в виде

Y = r ( t ) cos ϕ ( t ). (15)

Очевидно, что чем выше требования к точности измерений (чем меньше отношение сиг-нал/помеха), тем выше должен быть порядок приближения. Так, например, уже на уровне второго приближения необходимо учитывать инерционную и ступенчатую нелинейности [8]. Таким образом, гипотеза об аддитивности смеси сиг-нал+помеха также имеет определенную область применения и не является достоверной при обнаружении слабых сигналов или при проведении высокоточных измерений.

Известно, что квадратичный закон детектирования не препятствует воспроизведению формы прямоугольных импульсов. Иначе обстоит дело при квадратичном детектировании колебаний, огибающая которых является непрерывной функцией времени, как это имеет место, например, при передаче речи, музыки и других сигналов сложной формы, содержащих большое число частот, гармоники и комбинационные частоты. Тогда гильбертова огибающая существенным образом отличается от математической огибающей, что очень сильно влияет на разборчивость и тембр сигнала и делает применение квадратичного детектирования нецелесообразным в тех случаях, когда требуется неискаженное воспроизведение сигналов (речи, музыки и т. д.). Альтернативой гильбертовой огибающей является математическая огибающая, под которой понимается касательная процесса в его экстремальных точках. Так как задача обнаружения сигнала по существу сводится к задаче измерения конечных приращений, то математическим фундаментом таких измерений является теорема о конечных приращениях (теорема Лагранжа), согласно которой:

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна такая точка c, a < c < b, что fb) -fa) = f ‘(c)(b - a). (16)

Отметим непосредственную связь приращения функции, производной и касательной на интервале [ a , b ].

Теорема Лагранжа позволяет реализовать цифровые приемные системы не на основе интегрального исчисления, а на основе исчисления конечных разностей, одним из важных достоинств которого с точки зрения борьбы с помехами является исчисление конечных разностей вперед (т. е. в будущее), или экстраполяция, и исчисление назад (в прошлое), или ретрополяция.

С точки зрения общей теории колебаний основная разница между помехой и сигналом состоит в том, что помеха существует постоянно , а сигнал появляется эпизодически . Тогда, используя теорию о сингулярности и методы исчисления конечных разностей, помеху можно изучить с необходимой степенью достоверности и прогнозировать ее значение на текущий момент времени, обеспечивая наилучшие условия приема сигналов.

В функциональном пространстве C 2 [ a , b ] целесообразность и полезность конструктивного подхода достаточно хорошо обоснованы в литературных источниках [9–13], и нет необходимости останавливаться на этом вопросе подробно. Изложим только краткие основы предлагаемого нами адаптивного статистического конструктивного анализа и вытекающих из него особенностей конструктивного детектирования.

ИНФОРМАЦИОННО-ФИЗИЧЕСКАЯ МОДЕЛЬ И КОНСТРУКТИВНЫЙ АНАЛИЗ ОДНОУРОВНЕВЫХ МОДЕЛЕЙ

Рассмотрим приемно-излучающую систему как систему некоторого множества агрегатов, объединенных в единую систему по некоторому информационному признаку. Предположим, что каждый из этих агрегатов описывается нелинейными уравнениями Ван-дер-Поля. Модель сигнала сложной формы следует представить как линейную композицию нелинейных элементов, т. е.

N s (t) = ^ C( t )cosUi( t).          (17)

i = 1

Учитывая, что в такой системе присутствует все множество шумов (дробовых, тепловых, флик-керных, измерительных и т. д.), следует считать количество уровней огибающих в смеси сиг-нал+помеха теоретически ничем не ограниченным, т. к. всякий колебательный процесс имеет свою касательную в экстремальных точках. Однако в соответствии с нормой функционального пространства C 2 [ a , b ] в большинстве случаев можно ограничиться двумя уровнями огибающих, т. е. первой и второй производными.

Конструктивный анализ одноуровневых моделей. Для примера рассмотрим конструктивный анализ одноуровневых моделей.^*) Ключевым элементом конструктивного анализа является выделение сингулярных составляющих (скрытых периодичностей). При этом под реализацией понимается изменение параметра между двумя точками устойчивого равновесия (точками минимума) (см. Приложение, рисунки).

В основе конструктивного анализа лежит метод временнóй свертки первого порядка. Конструктивный характер временнóй свертки определяется тем, что дополнительно к операциям сдвига и статистического усреднения вводится операция селекции выборочных функций по параметру или их совокупности. В простейшей модели случайного процесса x ( t ) конструктивная временнáя свертка может проводиться по параметру T , для чего весь диапазон изменения параметра разбивается на n поддиапазонов, включающих в себя значения параметра T в промежутках:

[ T 1 , T 2 ], [ T 2 ,T 3 ], …, [ T k , T k +1 ], (18) что, по существу, определяет базис конструктивного анализа. Поддиапазоны определяются как расстояния между экстремумами смеси сиг-нал+помеха или ее огибающих различных порядков. При этом минимальное значение параметра T равно

T min = 1 / 2 f в , (19)

где f в — верхняя часть спектра сигналов. За величину T min следует принять минимальное расстояние между экстремумами сигнала.

В соответствии с (18) операцией сдвига по оси t формируется k амплитудно-фазовых случайных процессов:

X x (t) = { X i (т)}, i = 1, да , (20)

где входящие в него случайные процессы x k ( τ ) удовлетворяют условию (18).

Совокупность случайных процессов, образованных на основе одной бесконечно длинной реализации, называется амплитудно-фазовым случайным процессом (АФП).

Если для каждого случайного процесса (20) определить математическое ожидание или его оценку, т. е. зависимость вида да

M^k [ Х 1 ( т )] = Е m k ( т - T k ) ,          (21)

к = 1

то его можно рассматривать как конструктивное математическое ожидание случайного процесса x ( t ), а по аналогии с классическими методами анализа трактовать как конструктивный спектр, базисом или элементами которого являются функции m k ( τ ), в которых отображена информация о законах изменения мгновенных значений случайного процесса x ( t ). В последовательности T 1 , T 2 , …, T n отображена информация о фазовом спектре случайного процесса x ( t ), а в математической огибающей конструктивного спектра — информация об энергетическом вкладе каждого элемента конструктивного спектра. Таким образом, даже в простейшем случае конструктивного анализа конструктивный спектр содержит несоизмеримо больший объем информации о случайном процессе, чем аналогичные теоретико-множественные виды анализа. Это позволяет на качественно новом уровне решать весь комплекс задач, связанных с обнаружением и приемом сигналов, распознаванием образов и определением координат целей.

ЗАКЛЮЧЕНИЕ

Следует отметить, что предлагаемые методы конструктивного детектирования позволяют получить выигрыш в помехоустойчивости на основе критерия Неймана—Пирсона не менее чем на 6 дБ и ничем его не ограничивают.

С другой стороны, методы конструктивного детектирования и анализа не отвергают и не опровергают ничего из уже достигнутого в современной теории потенциальной помехоустойчивости, но расширяют и дополняют возможность ее использования. Однако становится совершенно ясной нецелесообразность финансирования тех работ по совершенствованию и модернизации современных радиоэлектронных средств, которые не позволяют преодолеть указанные в данной работе фундаментальные ограничения.

Приложение

АМПЛИТУДНО-ФАЗОВЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС: ПРИНЦИП ПОСТРОЕНИЯ КОНСТРУКТИВНОГО СПЕКТРА

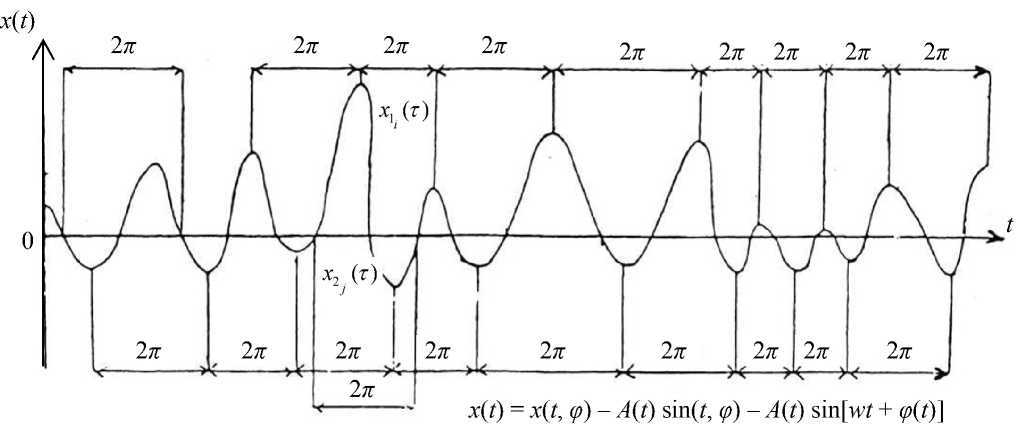
Ансамбль реализуется при постоянном фазовом интервале 2 π . Обязательное условие — формирование функционального пространства

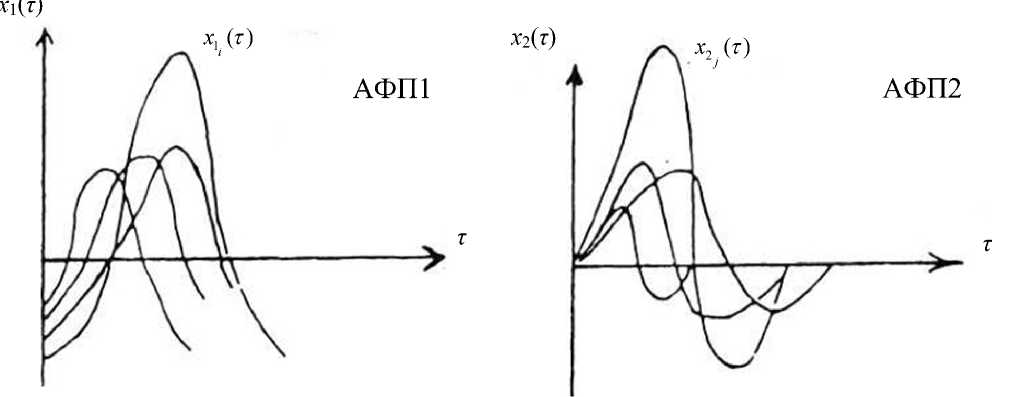
Конструктивная свертка 1-го порядка (пример 2).

Конструктивная свертка 1-го порядка (пример 1).

х1(т) = {x1 (т)}, где i = 1, да и на концах выборочных функций выполняются условия минимума:

x ‘(ti) - x ‘(ti+1) = 0, x"(t)>0, x"(t+i)>0

x 2 (т ) = { x 1 (т ) } , где j = 1, ^да и на концах выборочных функций выполняются условия:

x (tj) - x (tj+1) = 0, x'(tj) > 0, x'ttj+i) > 0

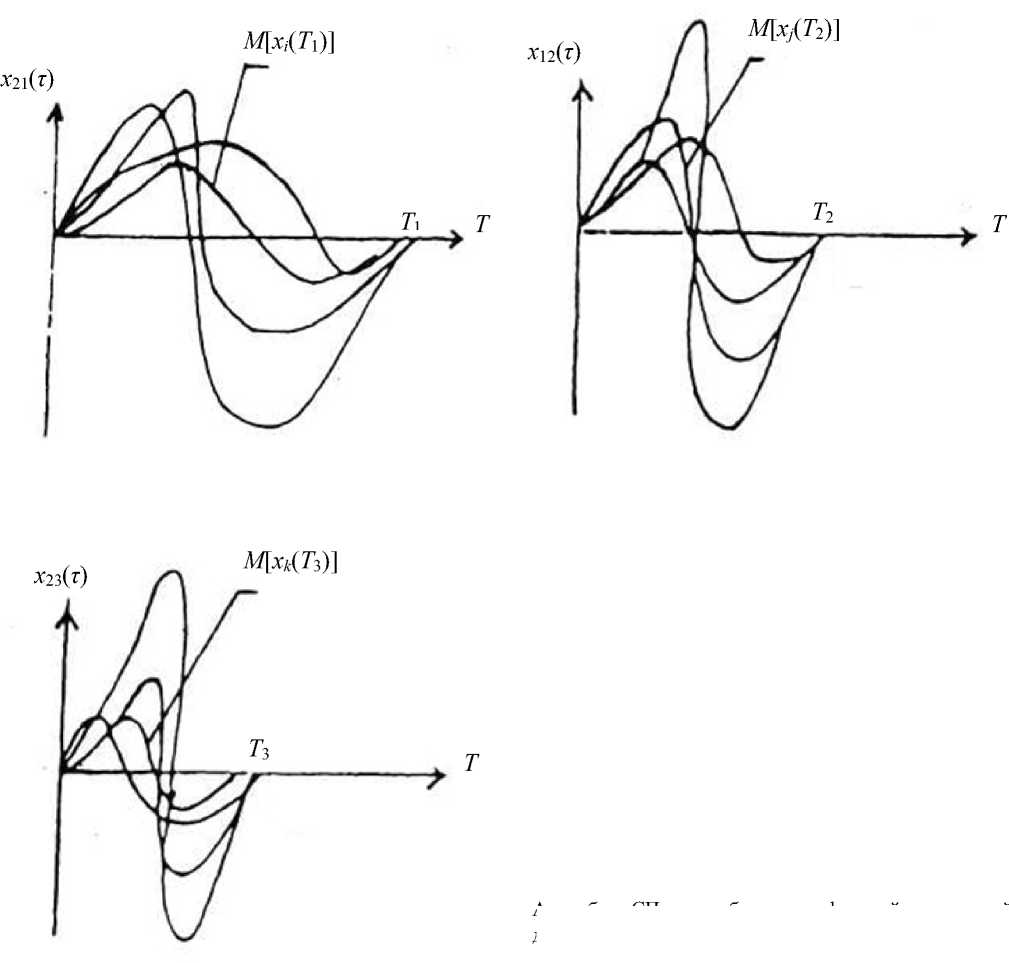
Ансамбли СП из выборочных функций одинаковой длительности (конструктивный АФП — x^k ( τ ))