Альфвеновский резонанс в дипольной магнитосфере с движущейся плазмой

Введение                                        В настоящей работе мы рассмотрим влияние

Одним из наиболее плодотворных в исследовани ях магнитосферных МГД - колебаний оказалось пред ставление о резонансных альфвеновских волнах . На возможность резонансной раскачки альфвеновских колебаний полем монохроматической быстрой маг нитозвуковой ( БМЗ ) волны впервые было указано в работе [1]. Впоследствии эта идея была подробно разработана во многих работах ( например , [2]).

Сначала теория магнитосферных МГД - колеба - ний была построена для простых магнитосферных моделей . В [3] использовалась модель магнитосфе ры в виде прямоугольного ящика . Силовые линии магнитного поля в этой модели предполагались прямыми , ограниченными двумя противоположны ми гранями , которые моделировали высокопрово - дящую ионосферу . Важным шагом в развитии тео рии альфвеновского резонанса стал переход к моде лям магнитосферы с дипольным магнитным полем [4]. Такие модели позволили изучить как эффекты кривизны силовых линий магнитного поля , так и неоднородности плазмы в направлениях вд оль маг нитных силовых линий и поперек магнитных оболо чек . Одним из отличительных свойств альфвенов - ского резонанса в дипольно - подобных моделях маг нитосферы является множественность резонансов , которые способна раскачать внутри магнитосферы монохроматическая магнитозвуковая волна [5]. При этом наибольшее число резонансных оболочек рас положено вблизи магнитопаузы .

Во всех выше перечисленных работах использо вались модели магнитосферы , в которых плазма покоилась . Как известно , в областях с большими градиентами скорости движения плазмы создаются условия для развития неустойчивости БМЗ - колебаний , которые могут возбуждать резонансные альфвеновские волны [6]. В магнитосфере Земли такие условия могут реализовываться на магнито паузе и плазмопаузе . Таким образом , движение плазмы может быть важным фактором , влияющим на резонансные альфвеновские колебания .

движения плазмы на структуру альфвеновского ре зонанса в дипольной модели магнитосферы , в кото рой движение плазмы моделируется ее азимуталь ным вращением . Особое внимание уделено пере ходной области между магнитосферой и солнечным ветром , где градиент движения плазмы и , соответст венно , его влияние на резонансные колебания мак симальны . При этом мы не рассматриваем магни тозвуковые колебания , которые являются источни ком резонансных альфвеновских волн , заменяя поле этих колебаний полем специально подобранного модельного источника .

Модель среды и основные уравнения

Для решения поставленной задачи используем магнитосферную модель с дипольным магнитным полем и азимутально вращающейся плазмой ( рис . 1). Аналитическое описание такой самосогла сованной модели дано в [7]. Вращение плазмы по зволяет моделировать как конвективное движение плазмы в магнитосфере , так и обтекание магнито сферы потоком солнечного ветра . Для описания альфвеновских колебаний в этой модели используем систему уравнений идеальной МГД :

dv             I . . _ _ _ p — = -V P +—[curl B x B], dt

^B = curl[vxB], 4 + V(pv) = 0, d-P = 0, dt                  dt                dt pY где B и v – векторы магнитного поля и скорости движения плазмы, Ри p - давление и плотность плазмы, у - показатель адиабаты.

Введем криволинейную ортогональную систему координат ( x ¹, x ², x ³), связанную с линиями магнит ного поля ( см . рис .   1). В этой системе

В0 = (0,0, B03), v0 = (0, v02,0), а элемент длины имеет вид ds2 = g,(dx У + g 2( dx2)2 + g 3( dx 3)2,

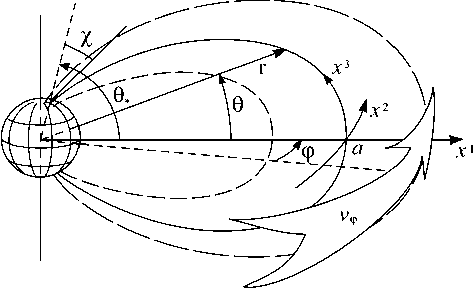
Рис . 1. Модель магнитосферы с дипольным магнит ным полем и азимутально вращающейся плазмой ( v = (0, v _φ ,0) ). Системы координат , связанные с силовыми линиями магнитного поля : криволинейная ортогональная 123

система ( x , x , x ) и неортогональная система координат ( a , φ , θ ), использованная в численных расчетах .

где g_i ( i = 1, 2, 3) – компоненты метрического тензо ра . Если в качестве азимутальной координаты ис пользовать азимутальный угол φ ( x ² = φ ), то v ₀₂ ≡ v _φ = g ₂ Ω , где Ω – угловая скорость вращения плазмы . Плазма на каждой магнитной оболочке движется с постоянной скоростью Ω ≡ Ω ( x ¹).

Линеаризуем систему уравнений (1), (2) относи тельно малого возмущения , связанного с МГД - колебаниями . Будем рассматривать монохроматиче ские колебания вида exp( - i ω t + ik ₂ x ²) , где ω – час тота колебаний , k ₂ – азимутальный волновой вектор ( если x ² = ф , то к ₂ — m = 0 ,± 1 ,± 2 ,... - азимутальное волновое число ).

Первые две компоненты (1) приводят к pQ2

-ρ ₀( i ω v ₁ + v ₂ Ω∇ ₁ln g ₂) - ₂ ∇ ₁ g ₂ =

= -V P - B. -к(Уз B -Vi B3),

1      4π g3     3 11 3

∇ ( g Ω ) v Ω

ρ0(-iωv2 +v1 1 2   + 3 ∇3g2) = g1

= -ik2 P - B0      (ik2 B3 - V3B2),

4 π g ₃

где ∇ _i ≡ ∂/∂ xⁱ ( i = 1, 2, 3), v_i и B_i – компоненты воз мущенных скорости и магнитного поля , P и р - возмущенные давление и плотность плазмы . Допол нительно введено обозначение ω = ω- m Ω – часто та колебаний , модифицированная эффектом Доп плера во вращающейся плазме .

Для дальнейшего описания МГД - колебаний удобно перейти от компонент электромагнитного поля и возмущенной скорости к потенциалам . Со гласно теореме Гельмгольца , произвольное векторное поле может быть представлено в виде суммы потен циального и соленоидального полей . Представим возмущенное электрическое поле колебаний в виде

E = -∇ϕ+ curlΨ, где ϕ – скалярный потенциал, а Ψ = (ψ1,ψ2,ψ3) – векторный потенциал. E инвариантно к добавлению произвольного градиента к векторному потенциалу Ψ → Ψ + ∇χ, при этом можно выбрать ∇χ так, чтобы ψ1 +∇1χ =0, т. е. Ψ = (0, ξ, ψ), где ξ =ψ2 + ∇2χ, ψ = ψ3 + ∇3χ.

Подставляя эти выражения в (3), (4), после неко торых преобразований можно получить следующее уравнение :

∇1LˆT(∇1 -(lnω)′)ϕ-k22LˆPϕ=LˆFψ, где

ˆ1      pω

L_T =     ∇ ₃      ∇ ₃ + p ₂ ,

• g3      g3

• -12

• ˆ      1 p

L_P =     ∇ ₃      ∇ ₃ + p ₂ –

• g3      g3

тороидальный и полоидальный продольные опера торы , g = g ₁ g ₂ g ₃, p = g ₂ / g ₁, A = B ₀ / 4 πρ ₀ – альфвеновская скорость . Выражение для оператора L ^ˆ _F из - за громоздкости здесь не приводится .

При переходе к однородной неподвижной плазме правая часть (5) обращается в нуль . Левая часть (5) при этом дает дисперсионное уравнение для альф - веновских волн : to ² - k ² A ² = 0. Как будет показано далее , поле колебаний , связанных со скалярным по тенциалом ϕ , д оминирует вблизи резонансной по верхности . Их поляризация соответствует альфве - новским волнам . Правая часть (5) описывает БМЗ - колебания и выступает в роли источника резонанс ных альфвеновских волн .

Структура резонансных альфвеновских колебаний вдоль силовой линии

Предположение о мелкомасштабности рассмат риваемого решения поперек магнитных оболочек позволяет использовать метод разных масштабов :

ϕ = V ( x ¹)( T ( x ¹ , x ³) + τ ( x ¹ , x ³)) exp[ ik ₂ x ² - i ω t ] , (6) где функция V ( x ¹) описывает мелкомасштабную структуру решения поперек магнитных оболочек , а T ( x ¹ , x ³ ) – структуру вдоль силовых линий магнит ного поля ( масштаб изменения этой функции по x ¹ сопоставим с масштабом неоднородности среды и много больше , чем масштаб функции V ( x ¹) ), τ ( x ¹ , x ³) – поправка следующего порядка теории возмущений . Оставляя в (5) только основные сла гаемые , пропорциональные ∇ ₁ ² V ( x ¹) , в главном по рядке получим уравнение

LT(to)T4 p £+p % T=0 (7) описывающее структуру альфвеновских колебаний вдоль силовых линий геомагнитного поля. Здесь l -длина силовой линии, отсчитываемая от экватора (dl = Vx3dx3). В этом приближении ионосферу можно считать идеально проводящей, что приводит к граничным условиям T(x1, l ±) = 0 , где знаки ± относятся к ионосферам Северного и Южного полушария соответственно. Решением уравнения (7) являются собственные функции TN(x1,l) и соответствующие им собственные значения ω= ΩN , где N = 1, 2, 3... – номер продольной гармоники колебаний.

∂ V N _≈    f N    exp[ i Ψ ( ∞ )]

∂ξ   κ _N β _N    ξ+ i ε    ^,

V N ≈    ^{f N}   exp[ i Ψ ( ∞ )]ln( ξ + i ε ) .

κ _N β _N

Поперечная структура резонансных альфве-новских колебаний

Теперь рассмотрим структуру альфвеновских колебаний поперек магнитных оболочек в окрестно сти резонансной поверхности . Подставляя в (5) ре шение в виде (6) и учитывая полученное из (7) ре шение для функции T = T_N ( x ¹ , l ) , в следующем по рядке теории возмущений в окрестности резонанс ной поверхности x ¹ = x_T ¹ _N получим уравнение ^∂ ( ξ + i ε ) ^{∂ V N} + d_N ( ξ+ i ε )^{∂ V N} -κ ² _N [1 +β _N ( ξ+ i ε )] = if_N , ∂ξ ∂ξ            ∂ξ

(8) где ξ = ( x ¹ - x_T ¹ _N ) / a – безразмерная координата ,

Очевидно , что поле резонансной альфвеновской волны имеет хорошо известную особенность при ε→ 0.

γ _N = ₂ ω

p ₊ v ₊

Г d T v ( d l

l +

+ p _- v _-

∂ T N ∂ l

l _-

мнимая добавка к частоте ( декремент колебаний ), полученная из граничных условий на ионосфере в этом порядке ,

a = [(ln Ω _N ( x ¹)) ′ ] ^{- 1} x ¹ = x T ¹ N , ε=γ _N / ω , f_N = a ² µ _N / ω ²,

^Ω′         2    ^α N 2 2        α N 2

d_N =     k ₂ a , κ _N =     k ₂ a , β _N =    Ω _N ,

ΩN         Ω2N          αN c2cosχ v±= 4πΣ±p±, l+ a N =-/ TN"dpF d l, l +    -1 2

aN = J pT dl, ^N = J Tn (k2 LFoV + LF1V) dl, l- Al

Найдем решение этого уравнения с помощью фурье - преобразования , представляя V_N ( ξ ) в виде

Обсуждение

Исследуем численно резонансные альфвеновские колебания , возбуждаемые в магнитосфере с диполь ным магнитным полем монохроматической быстрой магнитозвуковой волной . На рис . 2 представлено распределение нескольких первых собственных час тот стоячих альфвеновских волн поперек магнитных оболочек Ω _N ( x ¹) . Здесь же представлено распреде ление функций ω = ω- m Ω ( x ¹) для нескольких зна чений азимутального волнового числа m и фиксиро ванной частоты магнитозвуковых колебаний f = ω/ 2 π = 10 ^{- 2} Гц . Точки пересечения этих функ ций определяют местоположение резонансных по верхностей . Наиболее плотно резонансные поверх ности расположены в переходной области магнито сферы вблизи магнитопаузы .

Определим физическую компоненту магнитного поля альфвеновских колебаний с наибольшей ам плитудой на резонансной оболочке как B_y = B ₂ / g ₂ =| B_y | exp( i α _y ) . Рассмотрим распреде ление фазы резонансных колебаний α _y поперек резонансной оболочки L = 10, где градиент ∇ ₁ Ω ( x ¹) максимален ( рис . 3, a ). Фаза α _y меняется поперек резонансного слоя немонотонно и после возрастания на величину ~ π начинает уменьшаться . На рис . 3, б

1 ^∞

V_N ( ξ ) =         V ^% _N ( k ) exp( ik ξ ) dk .

2 π -∞

Подставляя его в (8), мы получим дифференци альное уравнение первого порядка на V_N , которое легко разрешимо . Тогда возвращаясь к V_N ( ξ ) , мы окончательно имеем :

V N ( ξ ) =-

f_N κ _N β _N

∞

J

exp[ ik ( ξ + i ε ) + i Ψ ( k )] k ² - id_Nk + κ ² _N β _N

dk , (9)

где

Ψ ( k ) =

κ ² + d / 2          k κ ² N β N + d N ² / 4

^{N N} arctan ^{N N N} κ ² _N β _{N + dN} ² _{/ 4}         κ _N β _N - ikd_N / 2

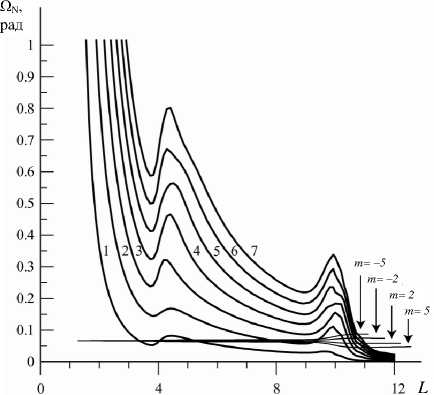
Рис . 2. Распределение собственных частот Ω _N первых гармоник стоячих альфвеновских волн ( N = 1, 2,K , 7 ) поперек магнитных оболочек и величины ω = ω- m Ω ( x ¹) для f = ω / 2 π = 10 ^{- 2} Гц и m = ± 2, ± 5 . Точки пересечения этих функций определяют местоположение резонансных поверхностей .

Рассмотрим поведение полученного решения в окрестности резонансной поверхности ξ = 0. Вблизи нее большая часть интеграла (9) набирается при k → ∞ . Полагая k → ∞ в знаменателе подынте грального выражения , получим

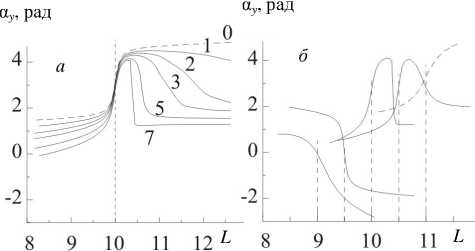
Рис . 3. Распределение фазы резонансных альфвен ских колебаний α _y поперек магнитных оболочек . На рис . 3, a представлено распределение α _y в модели с движущей ся плазмой на магнитной оболочке L = 10 для гармоник N = 1, m = 1, 2, 3, 5, 7, а также в случае неподвижной плаз мы ( Ω = 0) ( что аналогично выбору m = 0). На рис . 3, б представлено распределение α _y для гармоники N = 1, m = 7 на различных резонансных оболочках внутри переход ного слоя .

представлено распределение a y ( x 1 ) для гармоники N = 1 , m = 7 на разных резонансных магнитных оболочках внутри переходного слоя 9 <  L <  11. Чем выше градиент скорости движения плазмы , тем бо лее выражено его влияние на фазу резонансных ко лебаний . Немонотонное поведение фазы резонанс ных альфвеновских колебаний может служить ин дикатором области с большим градиентом скорости фоновой плазмы .

На рис . 4 представлены аналогичные распреде ления амплитуды резонансных колебаний | B y | внутри переходного слоя . В этих расчетах использо вано решение уравнения (8) с единичной правой частью f_N = 1. Декремент колебаний полагается при этом малым , чтобы выявить их резонансную структуру . На рис . 4, a приведены распределения амплитуды основной продольной гармоники резо нансных колебаний . Эффект движения плазмы здесь возрастает с увеличением m , хотя и менее выражен , чем для фазы рассматриваемых колебаний . Он за ключается в появлении асимметрии профиля рас пределения амплитуды . Для сравнения приведены распределения амплитуд тех же резонансных коле баний без учета движения плазмы ( т . е . при Q = 0). На рис . 4, б представлены профили амплитуды ре зонансной гармоники N = 1 , m = 5 на разных маг нитных оболочках внутри переходного слоя . Здесь же приведен профиль угловой скорости вращения плазмы Q ( x ¹).

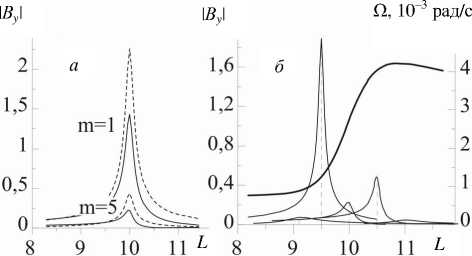
Рис. 4. Распределение амплитуды резонансных альф- веновских колебаний By поперек магнитных оболочек.

На рис . 4, a представлено распределение B_y ( x ¹ ) на маг нитной оболочке L =10 для гармоник N = 1, m =1, 5 как в модели с движущейся плазмой , так и в случае неподвижной плазмы . На рис . 4, б представлено распределение внутри переходного слоя B_y ( x ¹ ) для гармоники N = 1, m = 7 на различных резонансных оболочках ( правая ось ), а также угловой скорости плазмы Q ( x 1 ) ( левая ось ).

Работа частично поддержана грантами РФФИ 06-05-64495 и 07-05-00185 и Программами Прези диума РАН № 16 и ОФН РАН № 16.