Алгоритм реконструкции трехмерных объектов по двум изображениям

DOI:

В современном обществе информационные технологии каждый день продвигаются вперед и уже применяются практически в каждой сфере жизни человека [13]. Появляются новые способы шифрования и обмена данными, постоянно на основе старых технологий создают что-то новое, а также появляются новые направления информационных технологий. С таким развитием информационных технологий развиваются и другие смежные дисциплины, например, такие, как аналитика, программирование, проектирование, нейронные сети, компьютерное зрение и другие, по словам авторов [10].

Компьютерное зрение — это область искусственного интеллекта, которая обучает компьютеры интерпретировать и понимать визуальный мир. Используя цифровые изображения с камер и видео и модели глубокого обучения, машины могут точно идентифицировать и классифицировать объекты — а затем реагировать на то, что они «видят» [11]. Если рассматривать компьютерное зрение, как технологическую дисциплину, то можно сказать, что основная задача — это создание системы компьютерного зрения с применением теории и моделей (подробнее см. в статье: [12]). Машинное зрение — это попытка смоделировать механизм получения и обработки визуальной информации в человеческом мозге (описано в статье: [9]). Компьютерное зрение сосредоточивается в основном на обработке изображений. В первую очередь происходит оценка изображенного объекта, а следовательно поиск и обработка отдельных точек [7].

1.    Задачи компьютерного зрения

Научный прогресс идет по двум направлениям: экспериментальное и теоретическое. На экспериментальном рубеже исследователи выполняют некоторую комбинацию исследовательской экспериментальной работы и формальной проверки гипотез, как написали авторы [8]. В исследовательской экспериментальной работе проводятся эксперименты и собираются данные в надежде, что в них можно будет расшифровать некую закономерность, которая позволит выдвинуть формальную гипотезу для проверки. В режиме проверки гипотезы эксперименты проводятся путем явного создания некоторой контролируемой ситуации и проверки того, согласуются ли полученные наблюдения с тем, что можно было бы ожидать, если бы гипотеза была верна (подробно: [1]). Гипотеза может быть предположением, законом, который следует из теории, или проверкой гипотезы, которая пытается воспроизвести результаты ранее проведенного эксперимента. На теоретическом рубеже исследователи выполняют определенную комбинацию синтеза экспериментальных данных и существующей теории в более полную последовательную и общую теорию. Язык теории выражается в математической форме во всех естественных науках, как описывают авторы [4]. Как наука, компьютерное зрение имеет свои экспериментальные и теоретические аспекты. В теории науки компьютерного зрения можно ожидать законы и принципы, на основе которых компьютерные алгоритмы могут быть разработаны для решения разнорабочих задач технического зрения, таких как промышленный контроль, сборка роботов, автономная навигация транспортных средств и общее понимание трехмерных сцен [6]. В экспериментальных результатах, представленных в архивной научной литературе по компьютерному зрению, можно ожидать найти четкое описание контролируемых ситуаций, в которых проводились эксперименты, точное изложение используемого алгоритма и изложение результатов, включающее некоторую меру достоверности заявленных результатов. В теоретических результатах, представленных в архивной научной литературе, можно было бы ожидать найти множество частичных или неполных теорий, каждая из которых дает точное изложение конкретной проблемы компьютерного зрения, которую рассматривает теория (подробнее: [2]). Содержание теории должно развивать набор законов, принципов и связанных с ними алгоритмов, которые логически исходят из начальной постановки проблемы и предложений, относящихся к реальности, которую рассматривает теория [5]. Алгоритмы принимают на вход соответствующее изображение или изображения и выполняют вычисления, которые дают ответ, правильный по модулю количества шума в данных и адекватный теории, что подробно описывают авторы [3].

2.    Описание алгоритма

Математической моделью камеры является плоскость, заданная уравнением

(x, ^) = d, и точка О E R3 — центр проекции на эту плоскость. При этом проекция п(х) точки x E R3 вычисляется по формуле

п(х) = О + t(x — О), где

, d —( О, (х — О, '

На первом шаге алгоритма на двух изображениях выделяют прямолинейные отрезки (ребра), формируя два массива точек — концов этих отрезков и два массива ребер — массивы двуместных кортежей со ссылками на первый массив точек. Алгоритм использует пиксельные координаты, поэтому, задействуя внутренние параметры камеры (будут описаны ниже), пиксельные координаты переводятся в глобальные (мировые) координаты для выполнения пространственных вычислений. Для реконструкции точки в пространстве необходимо сопоставить две точки на двух изображениях — указать, какие точки из двух массивов представляют проекцию одной какой-либо точки в пространстве. В этом случае реконструкция происходит несложно — требуемая точка является точкой пересечения лучей г 1 , г ₂ , проходящих через точки изображений и выходящих из соответствующих центров проекций (см. рис. 1). Поскольку при переходе к пиксельным координатам происходит потеря точности из-за округления, то эти лучи могут не пересечься в пространстве. Поэтому находится точка р E R 3 как середина отрезка [ а,Ь] , на котором достигается минимум расстояния между точками лучей

• Р = ~+~ ,а,Ь = arg   min   |pi — р2|.

3.    Получение параметров для реконструкции

2                  P 1 E L ₁ ,p ₂ E L ₂

Далее для каждого выбранного ребра с концами в точках рп,рт на первом изображении строится два луча гп,гт в пространстве, выходящих из центра проекции и проходящих через концевые точки ребра, и вычисляется проекция п2(гп), п2(гт) этих лучей на второе изображение, используя внутренние параметры второй камеры. Для каждой такой проекции находятся точки, выбранные на втором изображении и лежащие на п2(гп), п2(гт). При этом ищется такая пара, которая образует ребро на втором изображении. После этого реконструируется в пространстве отрезок как реконструкция его концов (рис. 2).

Рис. 1. 3D-реконструкция точки по ее двум проекциям

Рис. 2. Пространственная реконструкция отрезка

Обозначим через L и N количество ребер и количество вершин на изображениях. Оценим алгоритмическую сложность предложенного метода. Для каждого ребра первого изображения вычисляются точки, попадающие на проекции соответствующих лучей на втором изображении. Это дает сложность O ( LN ) . Затем необходимо отобрать те пары найденных точек, которые образуют ребро на втором изображении. Это дает еще порядка L операций. В итоге общая сложность алгоритма оценивается как O ( L²N ) .

Для проведения тестирования алгоритма брались изображения из графического 3D-редактора Blender. Это обусловлено тем, что из данной программы имеется возможность получить нужные параметры об изображении и камеры, с помощью которой оно получено в результате рендеринга. Весь процесс реконструкции можно представить в виде блок-схемы на рисунке 3.

Для применения вышеописанного алгоритма из среды Blender извлекаются параметры камеры. Во-первых, это координаты в пространстве ( x,y,z ), которые задают центр проекции на плоскость камеры. Такой параметр можно получить проще, чем все остальные. Эти координаты берутся напрямую из интерфейса программы Blender (см. рис. 4).

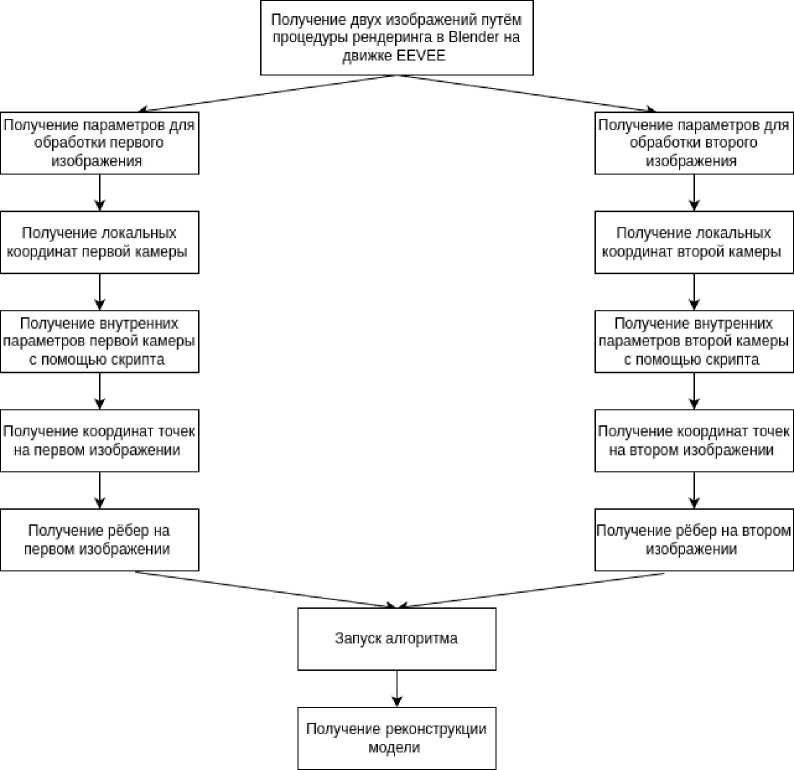
Рис. 3. Координаты центра проекции камеры

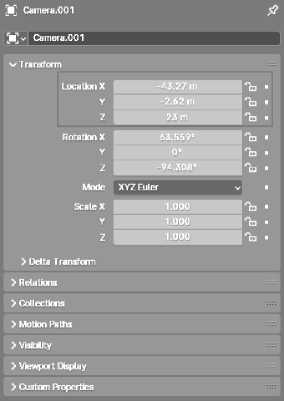
Рис. 4. Координаты центра проекции камеры

Во-вторых, дополнительные необходимые параметры представляют собой матрицу R размерности 3 x 3. Каждый столбец такой матрицы задает вектор ортонормированного базиса /1, f2, f3. При этом векторы /1, f2 задают базис в плоскости камеры, а вектор /3 — ортогонален этой плоскости. С помощью этой матрицы вычисляется проекция п(х) в пиксельных координатах X, Y по формуле x=4 х3

Y =

^ 2

^х 3 ’

где вектор х‘ = RT • х.

Для извлечения матрицы R необходимо воспользоваться встроенным модулем bpy, как это показано на рисунке 5. Главное назначение матрицы R — выполнять переход из глобальной (мировой) системы координат в систему координат камеры и обратно.

• 1    impart bpy

• 2    impart ninpy as пр

• 4    с name = "Camera¹'

• 5    сап = bpy .data, objects [спала]

• 6    pose - cam.matriK world

• &    print (pose)

• 9    pose = np.array(pose)

IQ R = pose[:3f:3]

• 12    print(R)

• 14    print (R.dot (R.I) J

Рис. 5. Внутренние параметры камеры — получение матрицы R

Далее опишем процесс создания массива точек на двумерном изображении. Как было показано выше, двумерные изображения получаются путем процедуры рендеринга в Blender на движке EEVEE (рис. 6).

Рис. 6. Пример получения двумерного изображения

Полученное изображение загружается в любой графический редактор для нахождения координат интересующих точек (см. рис. 7).

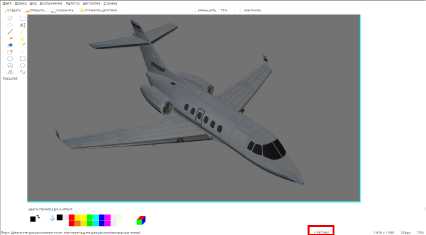
Рис. 7. Координаты точек

Путем ручного поиска множества точек получается массив координат ( х,у ) . Для удобства и возможности дальнейших изменений точки на изображении нумеруются (рис. 8). Координаты умножаются на масштабирующий коэффициент 0, 001 для удобного отображения после прохождения алгоритма в Blender (рис. 9).

Рис. 8. Пример изображения с пронумерованными точками

[[0.595,0.030], [0.640,0.052], [0.675,0.105], [0.745,0.074], [0.819,0.044], [0.870,0.077], [0.810,0.120], [0.721,0.176] [0.768,0.251],[0.814,0.315],[0.861,0.350],[0.881,0.334],[0.944,0.346],[1.016,0.378],[1.075,0.415],[1.083,0.444], [1.073,0.468],[1.082,0.477],[1.209,0.398],[1.356,0.292],[1.416,0.328],[1.333,0.455],[1.243,0.578],[1.428,0.700], [1.530,0.847],[1.599,0.980],[1.457,0.944],[1.324,0.880],[1.149,0.759],[1.075,0.728],[0.715,0.753],[0.271,0.780], [0.204,0.726],[0.528,0.664],[0.867,0.580],[0.843,0.558],[0.819,0.578],[0.776,0.575],[0.696,0.506],[0.653,0.434], [0.663,0.408],[0.715,0.415],[0.686,0.335],[0.698,0.328],[0.675,0.266],[0.647,0.185],[0.542,0.191],[0.392,0.204], [0.351,0.171],[0.484,0.145],[0.620,0.118]]

Рис. 9. Массив координат точек

И еще один, немаловажный параметр, массив ребер, то есть пары точек из предыдущего массива. Для получения этого массива и были пронумерованы точки на изображении (рис. 10). Если провести линии между точками из массива ребер, то получится контур нашего объекта, отображенного на двумерном изображении.

[[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9],[9,10],

[10,11],[11,12],[12,13],[13,14],[14,15],[15,16],[16,17],[17,18],[18,19],[19,20],

• [2 0,21],[21,22],[22,23],[23,24],[24,25],[25,26],[26,27],[27,28],[28,29],[29,30], [30,31],[31,32],[32,33],[33,34],[34,35],[35,36],[36,37],[37,38],[38,39],[39,40], [40,41],[41,42],[42,43],[43,44],[44,45],[45,46],[46,47],[47,48],[48,49],[49,50],[50,О]]

4.    Тестирование алгоритма

Рис. 10. Массив ребер

Тестирование алгоритма проходило на нескольких объектах разной формы. Для лучшей оценки качества алгоритма было решено для начала использовать более простые модели и в дальнейшем переходить к более сложным. Одним из тестов было решено взять простейшее сочетание двух фигур. На рисунках показаны результаты рендеринга с двух камер в Blender с подписанными точками (рис. 11 и 12).

Рис. 11. Изображение с первой камеры

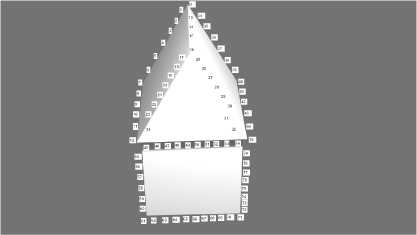
Рис. 12. Изображение со второй камеры

Заметим, что нумерация вершин на разных изображениях никак не согласована. Собственно вычисление такого сопоставления и есть предназначение алгоритма. Более того, отмеченные ребра также никак не связаны на этих изображениях — это тоже задача вышеописанного алгоритма. Результат реконструкции представлен на рисунке 13.

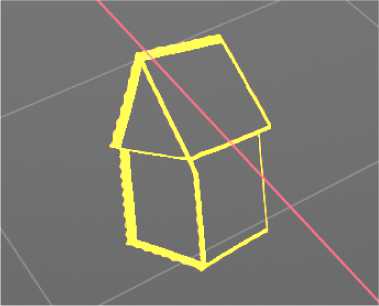
Рис. 13. Результат реконструкции

Также хотелось бы привести еще один результат тестирования. В этой работе уже был показан результат тестирования алгоритма. Теперь рассмотрим более сложные и интересные изображения. Так как на этом объекте очень много различных линий и это не настолько прямые линии, как в предыдущем тесте, поэтому стоит взять большое количество точек для более точного описания контура самолета на каждом из двух изображений. На рисунках представлены изображения с двух камер из программы Blender, а также пронумерованы точки (рис. 14).

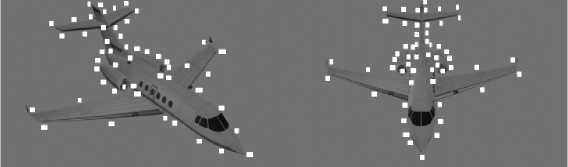
Рис. 14. Изображение с первой камеры

Результат работы реконструкции модели в тесте с самолетом (рис. 15).

Рис. 15. Результат реконструкции

Несмотря на то что в работе приведено всего два результата тестирования, было проведено намного больше запусков алгоритма, и получены различные результаты. Можно с уверенностью сделать несколько выводов. Во-первых, чем больше количество точек выбрано на границах объекта на изображениях, тем качественнее результат работы реконструкции. Во-вторых, если задействовать большее количество камер для получения снимков, тогда и результаты будут получаться более качественными.