Алгоритмическое исследование треугольника типа Паскаля и помехоустойчивые коды

Помехоустойчивое кодирование является актуальной в настоящее время задачей теории информации. Данной задачей занимаются криптография и дискретная математика. Каналы связи — не идеальные проводники для передачи информации, достаточно часты случаи изменения кодовых комбинаций из-за влияния шума или различного рода помех. Для исправления таких ошибок в код добавляют избыточные данные, например, биты четности в коде Хэмминга. На данный момент придумано множество помехоустойчивых кодов, каждый из которых имеет свои преимущества и область применения (например, [3] [4] [5] ).

• 1    Позиционная система счисления

Под позиционной системой счисления понимают систему счисления, в которой значение каждой цифры (базового элемента) может варьироваться в зависимости от позиции (разряда) в числе, где он находится. Количество элементов (основание системы) обозначается числом p, где p G N, p >  1 . Позиционную систему, в которой p элементов, будем называть p -ичной системой счисления. В такой системе используются цифры от 0 до p — 1 ; если p >  10 , то вводятся буквенные обозначения для базовых элементов.

Одним из важных и, пожалуй, интересных свойств является соответствие лексикографического порядка записей естественному порядку, но записи чисел должны быть слева дополнены ведущими незначащими нулями. Например, 101 2 и 1001 2 для сравнения этих чисел нужно дополнить нулями первое число 0101 2 и 1001 2 (видно, что уже в четвертом разряде чисел есть расхождение) 0 <  1 = ^ 0101 2 <  1001 2 .

Применение p -ичной системы достаточно эффективно с точки зрения затрат памяти и ресурсов компьютера или других устройств, где каждый базовый элемент отвечает за определенное состояние единицы информации в системе. Например, использование троичных алгоритмов в ЭВМ куда более эффективно с точки зрения плотности записи lnp информации, равной p , принимающей максимальное значение при p = е, но так как p G N, то при p=3.

• 2    Треугольник Паскаля

Треугольником Паскаля называют бесконечную треугольную таблицу, элементы которой являются числами сочетаний, иначе называемыми биномиальными коэффициентами. Данная структура содержит в себе и натуральные, и треугольные числа, и числа Фибоначчи [1] .

Числом сочетаний C ^k _n называется количество способов выбрать неупорядоченное k -элементное подмножество из n -элементного множества.

Ck =    —   , где n > k > 0 и n, k G Z k!(n — k)!

for (int i = 0; i <   ; : ++) {

Pascal_triangle [ ].resiz (  + 1);

Pascal_triangle[ ][0] = Pascal_triangle[ ][ ] = 1;

for ( .nt j = 1; j < i ; j ++) {

Pascal_triangle[ ][ ] = ((( ascal_triangle[i - 1][j - 1])) + (Pascal_triangl [  - 1][ ]))% ;

}

}

Данный алгоритм [1] реализует моделирование структуры треугольника с помощью рекуррентной формулы. Здесь числа хранятся в двумерном массиве, где i -й подмассив — это i -я строка треугольника Паскаля, числа в котором рассматриваются по модулю p .

Соответствующие нули при выводе в консоль заменим на «.» для визуальной красоты.

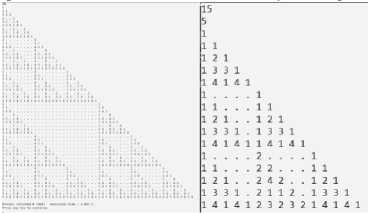
Рис. 1. Вывод структуры треугольника в консоль [1]

Элементы i -й строки треугольника представляют собой коэффициенты разложения степени бинома Ньютона ( a + b) i . Представление элементов треугольника Паскаля по модулю p позволяет нам заметить интересные свойства данной структуры, например, самоподобие треугольника, превращающее его во фрактал (треугольник Серпинского); мелкость разбиения зависит от p (например, [2] [7] ).

• 3    Помехоустойчивые коды

  В XXI в. в связи с развитием высокоскоростного Интернета резко возросла необходимость в системах передачи и хранения информации. Главной задачей в подобных системах является помехоустойчивая передача данных. До 1948 г. считалось, что наличие шумов в канале связи — камень преткновения в безошибочной передаче данных, пока Клод Элвуд Шеннон не опубликовал основополагающую работу по теории информации, в которой была показана принципиальная возможность

обеспечения надёжной передачи данных со скоростью, не превышающей пропускной способности канала. Однако теорема, сформулированная Шенноном, лишь доказывает существование таких кодов, но не объясняет, как такие коды строить и как декодировать [8] [9] [10] .

Если необходимо закодировать T сообщений равномерным p -ичным кодом, то нужно выбрать такую длину кодируемого сообщения n , чтобы выполнялось нестрогое неравенство T ≤ p ⁿ .

Данное неравенство называют граничным условием . В случае выполнения равенства при кодировании сообщений будут использоваться всевозможные p -ичные числа, в данном случае код не будет помехоустойчивым, ибо любая ошибка в комбинации повлечет за собой её смену на другую комбинацию, без возможности обнаружить ошибку. В случае строгого неравенства у нас есть возможность обеспечить длину строки n > k , где k — количество информационных элементов и k = log p T , в связи с чем появляется возможность выделить избыточные r = n - k элементов, которые будут необходимы для построения помехоустойчивого кода. Число n должно позволить получить T’ кодовых комбинаций Т’> T , из которых можно будет выбрать Т комбинаций, которые будут называться рабочими, а остальные — нерабочими. При получении нерабочей комбинации, во-первых, мы сразу будем знать об ошибке, во-вторых, сможем найти наиболее похожую комбинацию среди имеющихся и исправить ошибку [6] .

Избыточностью кода называют свойство кода, которое позволяет исправить ошибки, допущенные при передаче или приёме символов сообщения, она вычисляется по формуле:

g = ^r. (1) n

Необходимо реализовать формулу (1) в алгоритме, так как k — количество информационных элементов, значит, k должно быть целым, используя функцию ceil из библиотеки cmath, округлим значение k вверх: float redundancy_bonacci ( int T , int p , int n) { float k = (ceil((log(T) / log(p)))) ;

float g = (n - k) /n; return g ;

}

Введем несколько новых определений, необходимых для дальнейшего исследования.

Расстоянием Хэмминга d(x,y) между любой парой комбинаций x и y называют количество позиций, в которых они различаются. Больший интерес для нас представляет минимальное кодовое расстояние между последовательностями:

dmin = min{d(x, y) : Vx,y G T,x = y}.(2)

Реализуем данную формулу в алгоритме:

int hamming_distance_bonacci(vecto < n1 >  ,vector< in >) { int d = 0;

for (.nt i = 0; i < a.sizi () ;++){ if ( []!=![]){ d ++;

}

} return ;

} int d = cols + 1;

for (int i = 0; i < rows ;   + + ) { for (int j = 0; j < rows ; ; + + ) { if ( !=j ) { int a = hamming_distance_bonacci( like_pascal[L

] ,like_pascal [ ]) ;

if( >   ) {  = a;}

}

}

}

Если попытаться выделить кодовую таблицу из треугольника Паскаля, то получим прямоугольник Тартальи, у которого первая строка и первый столбец называются образующими и состоят из единиц, что значительно уменьшит количество уникальных последовательностей.

( 1 1 1 \

1 2 3

V ³ 6 )

В связи с этим рассмотрим треугольник типа Паскаля с образующими из последовательных натуральных чисел:

( 12 3 \

2 4   7                                  (3)

3 7 14

Кодом типа Паскаля длины p ⁿ называется код, задаваемый таблицей (3) размерности pⁿ x p ⁿ⁺¹ , если все элементы рассматриваются по mod p .

Для иллюстрации метода рассмотрим подобную таблицу 3 x 9 при p = 3 :

2 1 1

0 1 2

2 1 2

0 1 0

• 1    2 2

• 2    1 0

В данном случае d _mi_n = 1 , T < p ⁿ . Код является помехоустойчивым, но так как d _mi_n = 1 при воздействии шума мы не всегда сможем при получении сигнала найти и исправить ошибку, ибо при изменении одного элемента в комбинации мы либо получим другую комбинацию из кода типа Паскаля и вовсе не обнаружим ошибки, либо получим последовательность, которой нет в нашей изначальной таблице, и ошибка будет обнаружена. Теперь появилась необходимость в коде, который всегда будет обнаруживать хотя бы b ошибок.

При b = 1 , d _mi_n = 1 , так как при смене одной позиции в комбинации, во-первых, ошибка будет обнаружена, так как измененной последовательности заведомо нет в таблице, во-вторых, мы всегда сможем найти комбинацию, расстояние между которой и полученной будет равно 1. При b = 2 , d _mi_n ≥ 3 . В общем случае d _mi_n ≥ b + 1 . Заметим, что при b = n (изменение всех элементов последовательности) d _mi_n ≥ n + 1 , что невозможно обеспечить в данном коде.

Чтобы обеспечить наперед заданное минимальное расстояние, нужно выбрать рабочие комбинации. Для этого необходимо рассчитать всевозможные расстояния Хэмминга с помощью алгоритма:

vector < vector > dmin (rows , vector  ( rows) ) ;

int d = c ol s + 1 ;

for ( int i = 0 ; i < rows ; i++) { for ( int j = 0 ; j < rows ; j ++) { if (i!=j){ int a = hamming_distance_bonacci ( like_pascal [i ] , like_pascal [j]) ;

dmin [i] [j]=a;

cout <

if (d > a){d = a;}

} else{ dmin [i] [j ] =0 ;

cout <

}

} cout <

}

Для приведенного ранее примера (4) с помощью алгоритма все расстояния составим в виде таблицы 9 х 9, где в i-й строке будут даны всевозможные расстояния между i-й комбинацией и другими последо- вательностями.

033132123 302212311 320311221 123033132 311302212 221320311 132123033

21231 1302 311221320

Основываясь на этих данных, мы можем выбрать три рабочие комбинации.

2 1 1 \0 ¹2)

При увеличении числа обрабатываемых ошибок количество рабочих комбинаций уменьшается. Данный случай необходимо рассматривать на кодах типа Паскаля при больших значениях n.

Заключение

Результаты показывают перспективу применения p-ичной кодировки треугольника типа Паскаля при решении задач кодирования информации. Кроме того, получены помехоустойчивые коды типа Паскаля при различных p. Дальнейшие исследования будут направлены на изучение других помехоустойчивых таблиц, расширение и оптимизацию уже имеющегося алгоритма.